考慮河流流速和橫向擴散系數變化的污染混合區理論分析及其分類

武周虎

（青島理工大學 環境與市政工程學院，山東 青島 266033）

1 研究背景

市政、工業和其它來源的污/廢水經處理后，通過岸邊排放口泄入河流。在河流中經初始稀釋階段之后，污染物在垂向上可以達到均勻混合，再進入污染帶擴展階段。因此除近區以外，可以作為二維移流擴散問題處理［1-3］。通常應用物理模型或數學模型來研究污染帶的橫向擴展以及對于環境的影響，而橫向擴散系數（又稱橫向混合系數）是模型的重要參數和解決問題的關鍵之一［4-5］。在環境水力學中，常常是按照污染物濃度橫向分布服從正態分布規律，結合室內或現場試驗資料采用濃度矩法、直線圖解法、線性回歸法和模型演算法等方法［6-10］，或者采用基于剪切流分散理論的橫向速度與深度平均值的偏差流速［11-13］，來確定矩形斷面明渠和天然河流橫向擴散系數，其分析結果是將橫向擴散系數處理成常數，即橫向擴散系數在整個斷面上采用常數。長期的研究大多致力于尋求橫向擴散系數與河段（或斷面）平均水力學參數之間的半理論半經驗關系式［14-20］。在實踐中，通常采用常數橫向擴散系數來進行河流水環境影響預測和計算河流排污混合區［21-24］。

趙振祥等［25］通過采用斷面平均方法，對具有相同橫斷面面積、水面寬度、平均水深和平均流速的矩形與梯形斷面的擴散濃度分布比較發現，梯形斷面岸邊斜坡上的濃度明顯高于矩形斷面岸邊區域的濃度。Fischer H B等人［1］根據獨立實驗給出橫向擴散系數Ey∝h（其中h是平均水深），即水深淺的地方橫向擴散系數小，據此趙振祥等［25］提出橫向擴散系數在整個斷面上是變化的概念。并對萊茵河某河段的橫向擴散系數進行了計算，得出全斷面上無量綱橫向擴散系數為αy=0.20，岸邊污染帶（y=60 m）內的無量綱橫向擴散系數為αy1=0.14，相對誤差為30%。在大江大河中岸邊排放的污染帶通常位于具有斜坡的岸邊，斜坡上的橫向擴散系數與整個斷面上的平均橫向擴散系數是不一樣的。因此，采用整個斷面上的平均物理量去反映河流岸邊的局部地形特征，取橫向擴散系數為常數是不妥的。

由于在以往的河流橫向擴散系數確定中，常常是根據污染物濃度的橫向分布監測結果進行，忽視了對于河流移流擴散污染物二維濃度分布特征的監測分析，導致河流橫向擴散系數在整個斷面上的變化特征未得到應有的重視。直到武周虎等［26］和Wu等［27］基于河流平均流速和常數橫向擴散系數，在順直河流岸邊穩定點源條件下推導出二維移流擴散污染混合區邊界歸一化（等濃度）曲線方程才發現，據此得到的污染混合區形狀特征，如最大寬度對應的縱向坐標與最大長度之比等于1/e（數學常數e=2.7183），不能解釋黃真理等［28］在長江三峽建水庫前庫區水環境現狀及水文水質污染負荷同步觀測中得到的黃沙溪排污混合區形狀。事實上，污染混合區邊界曲線能很好地反映污染物的二維濃度分布特征，河流橫向擴散系數在整個斷面上的變化，會直接影響污染混合區邊界曲線的形狀特征［29-31］。

Wu等［29-30］分析了河流大渦紊動對“污染云”擴散的主導作用，參照有風時大氣擴散參數的指數形式，假定河流變橫向擴散系數Ey(x)=γxα，式中:γ，α為正常數。在順直河流岸邊穩定點源條件下，求解了二維移流擴散方程濃度分布的解析解，推導出污染混合區邊界曲線方程，給出最大寬度對應的縱向坐標與最大長度之比等于exp［-1（/1+α）］。雖然現場觀測的污染混合區最大寬度對應的縱向坐標位置，可以通過擬合變橫向擴散系數中的正常數指數α得到滿足，但是污染混合區形狀曲線的吻合程度還是相差較大［28］；Wu等［31］又分析了河流從岸邊到中間的流速和橫向擴散系數的變化特征，參照下層大氣水平流速和垂向擴散系數隨高度按指數律變化的經驗公式，假定河流深度平均流速和橫向擴散系數的橫向分布服從u=u1(y/y1)m，Ey=Ey1(y/y1)n，式中:u1和Ey1分別代表離岸橫向坐標y（1≤W/2）點的流速和橫向擴散系數值，W為河流寬度。在順直河流岸邊穩定點源條件下，求解了二維移流擴散方程濃度分布的解析解，推導出污染混合區邊界曲線方程。污染混合區最大寬度對應的縱向坐標相對位置與常數橫向擴散系數時相同，現場觀測的污染混合區形狀曲線的吻合程度，可以通過擬合流速和橫向擴散系數橫向分布的正常數指數m和n得到滿足。由此可以看出，單獨考慮橫向擴散系數隨縱向坐標x的變化，只能反映現場觀測的污染混合區形狀在縱向坐標方向的變化特征；而單獨考慮流速和橫向擴散系數的橫向分布，也只能反映現場觀測的污染混合區形狀在橫向坐標y方向的變化特征。因此，只有同時考慮以上兩種情況，才能全面反映現場觀測污染混合區形狀的二維變化特征。

針對上述問題，本文通過對長江黃沙溪排污混合區平水期同步觀測資料的分析，提出深度平均流速的橫向指數分布和橫向擴散系數的二維變化關系式。在寬闊河流順直岸邊穩定點源條件下，求解變系數二維移流擴散方程濃度分布的解析解，推導污染混合區最大長度、最大寬度和對應縱向坐標以及面積的理論公式，給出污染混合區邊界歸一化（等濃度）曲線方程。在結果分析基礎上，提出污染混合區的類別、分類條件和變橫向擴散系數的估算方法，可作為河流污染混合區范圍的計算依據，也可以對水質建模起到理論指導作用。

2 濃度分布求解與特性分析

2.1 流速和橫向擴散系數的關系式

（1）流速的橫向分布在分析了黃真理等［28］給出的長江三峽建水庫前庫區水環境現狀及水文水質污染負荷同步觀測中，黃沙溪排污混合段平水期6個斷面的深度平均流速橫向分布觀測值（如圖1數據點所示）的基礎上，對深度平均流速的橫向分布選擇指數分布規律［31］進行曲線擬合。

式中:u和u1分別為距離排放岸橫向坐標y點和y1（≤W/2）點的深度平均流速；W為河流寬度；m是正常數指數。

對于按順直河流進行簡化處理的黃沙溪排污混合段，將全部6個斷面的深度平均流速橫向分布觀測值一并采用指數分布式（1）進行回歸分析得到:y1=150 m，u1=1.4 m/s，m=0.25，相關系數R2=0.7483，其相關性較好，在圖1中以實線顯示。

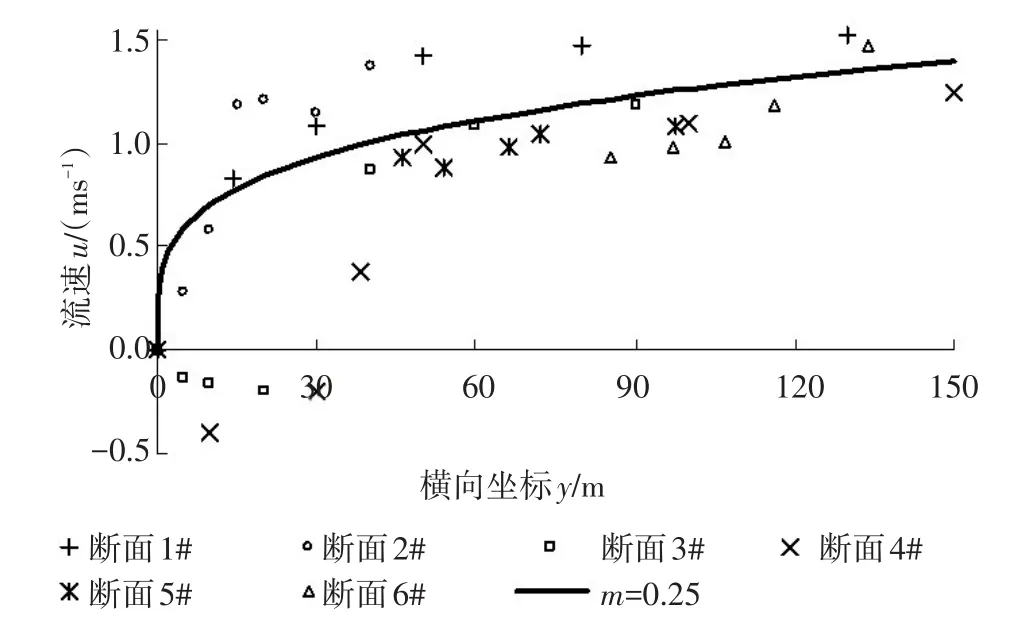
圖1 黃沙溪排污混合段平水期深度平均流速的橫向分布

（2）橫向擴散系數的關系式根據Wu等［29-30］對河流二維移流擴散問題的分析，從岸邊排污口排出的污染物擴散時間越長，遷移距離越遠，擴散范圍不斷增大，大尺度渦旋體的擴散作用逐漸增強。考慮到大渦對“污染云”擴散的主導作用，因此有橫向擴散系數隨著污染云的擴散范圍增大而增大，即河流橫向擴散系數與遷移距離x成比例。另一方面，由于河岸地形對水流的摩擦阻力作用，河流近岸區域的流速一般低于中間區域，離岸距離越大，流速越大，橫向擴散系數也越大。Wu等［31］根據河流深度平均流速的橫向指數分布規律，提出橫向擴散系數的橫向分布同樣服從指數分布規律。綜合以上兩種點，假設橫向擴散系數既服從橫向指數分布規律，又隨縱向坐標x呈指數變化的關系式為:

式中:Ey為從排放口沿水流縱向坐標x、距離排放岸橫向坐標y點的橫向擴散系數；γ、α、n均為正常數。

2.2 岸邊排放源在非均勻流場中的擴散根據張書農［4］、Wu等［31］和Li［32］在穩態條件下，對河流二維移流擴散方程的簡化處理，在離開排放口一定距離后的遠區，即xu?Ex，縱向坐標x方向的擴散項與移流項相比，在縱向上的擴散作用微不足道，可以忽略不計；按照一般環境水力學概念，河流中的橫向流速可以略去，在橫向上的污染物主要表現為擴散與混合。因此，河流中的簡化二維移流擴散方程為:

式中:x為自排污口沿河流流向的縱向坐標；y為垂直于x軸從排污口指向河心的橫向坐標；u為深度平均流速；Ex和Ey分別是縱向和橫向擴散系數；C為污染物濃度。

將式（1）和式（2）代入式（3），整理得到變系數二維移流擴散方程為:

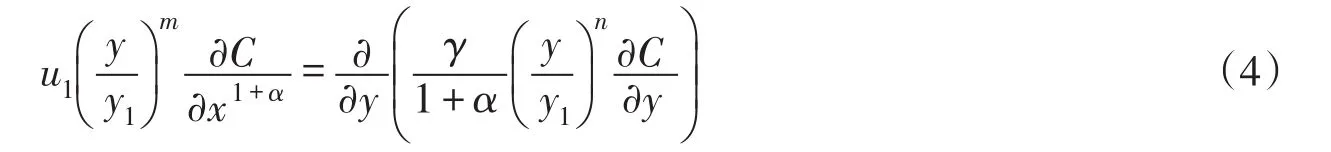
令X=x1+α，E=γ/( )1+α，式（4）變為:

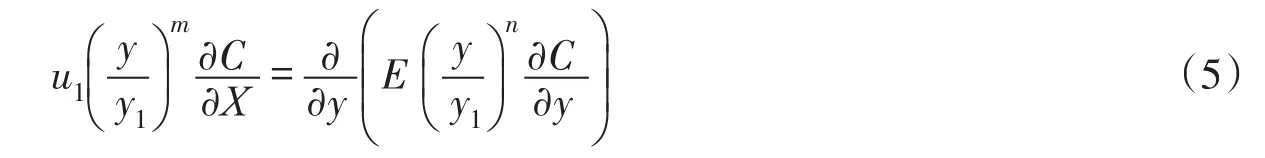
根據Wu等［31］在順直矩形河渠中，在岸邊穩定線源單位時間單位水深的排放質量m˙=M˙/H的條件下，對于保守物質，由式（5）給出深度平均流速和橫向擴散系數均服從指數分布規律決定的河流二維移流擴散污染物濃度分布為:

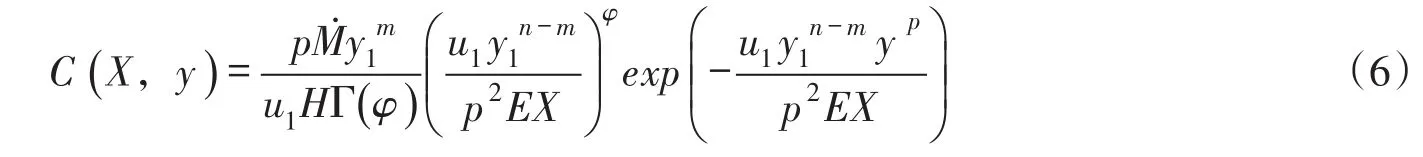
式中:p=2+m-n＞1；φ=（1+m）/p；Г（φ）為完全伽瑪函數；M˙為岸邊穩定點源單位時間的排放質量；H為平均水深。

將X和E代入式（6）整理得到，由深度平均流速的橫向指數分布式（1）和橫向擴散系數的二維變化關系式（2）確定的河流二維移流擴散污染物濃度分布為:

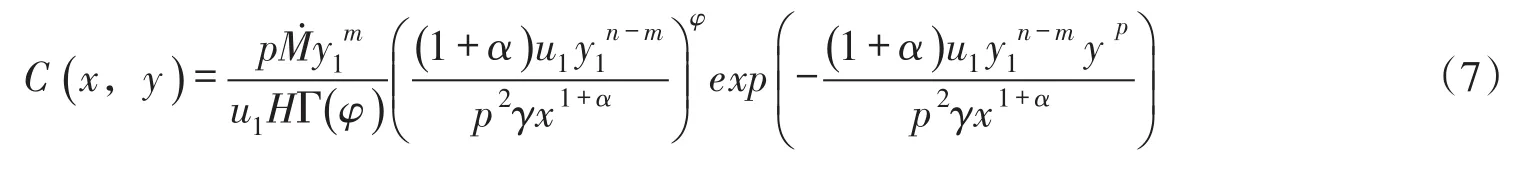
2.3 濃度分布特性分析由式（7）可以得到，對于縱向坐標的給定值（xi，i=1，2，3，…），河流岸邊排放二維移流擴散污染物濃度的橫向分布特征主要取決于exp（-yp）。即污染物濃度隨橫向坐標y的增大單調下降，橫向濃度分布曲線類似于半正態分布形式；當縱向坐標x增大時，橫截面上的最大濃度沿程逐漸減小，污染物濃度迅速在橫向上擴展，濃度梯度迅速減小，如圖2所示。

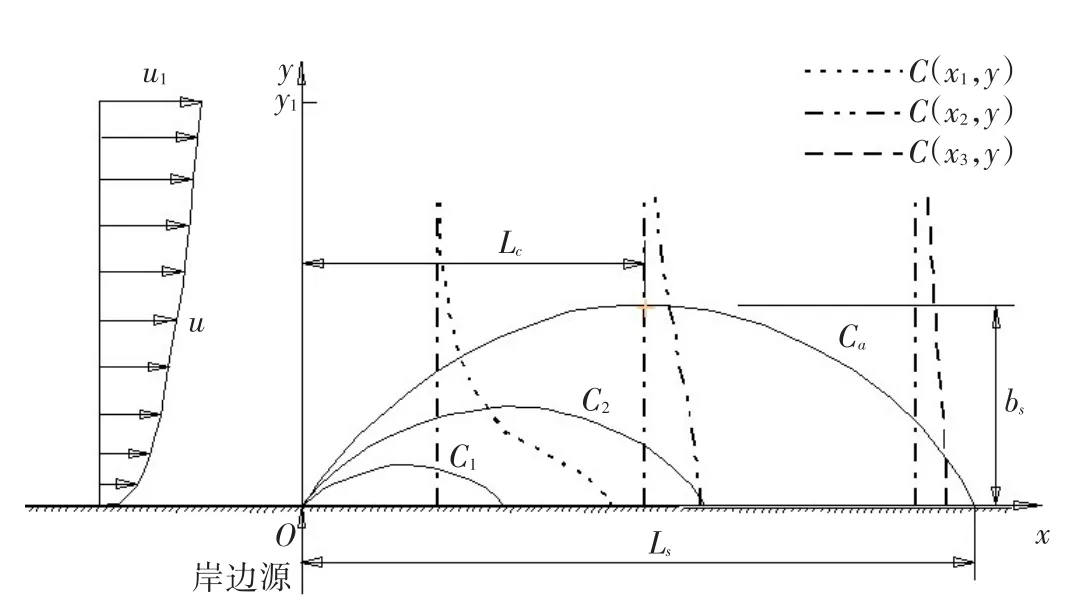
圖2 河流岸邊排放污染物濃度分布和等濃度線

令y=0，由式（7）可以得到橫截面上污染物最大濃度的沿程分布為:

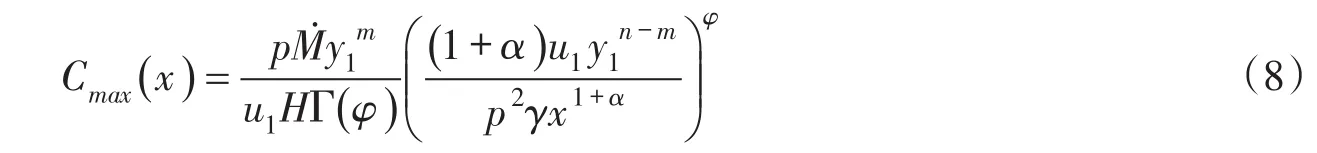
即橫截面上的最大濃度隨縱向坐標x的［-φ（1+α）］次方下降。

由于深度平均流速的橫向分布不是常數，因此，河流中污染物濃度的橫向分布不能代表污染物通量q（xi，y）=uC的橫向分布。對于保守物質，在縱向坐標取任意值（xi）時，則有河流各斷面的污染物總通量相等，即有:

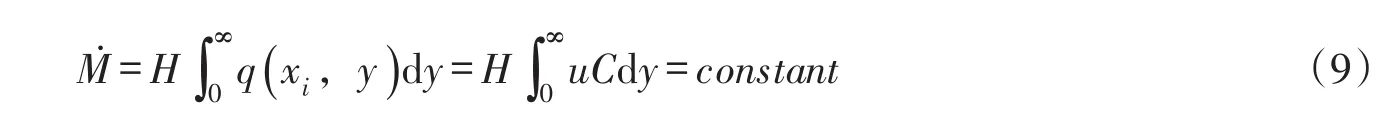
當α=0時，橫向擴散系數與縱向坐標x無關，橫向擴散系數和深度平均流速的橫向分布均服從指數規律，式（7）變為與相同條件下Wu等［31］給出的結果一致；當m=n=0時，橫向擴散系數和深度平均流速均在橫向上保持常數，橫向擴散系數僅隨縱向坐標x呈現指數變化規律，式（7）變為與相同條件下Wu等［29-30］給出的結果一致；當α=m=n=0時，橫向擴散系數和深度平均流速均取常數，式（7）變為與相同條件下Wu等［26-27］給出的結果一致。

3 污染混合區幾何特征

根據污染混合區的概念，河流背景污染物濃度Cb與排放產生的允許升高濃度Ca的總和應符合水環境功能區所執行的濃度標準值Cstd，即有Ca=Cstd-Cb，該等濃度線所包圍的區域稱為污染混合區。

由式（7）可知，河流岸邊排放的污染混合區邊界（等濃度）曲線方程為:

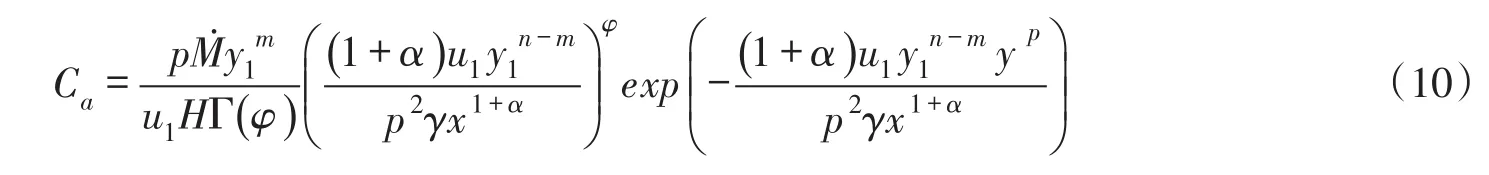
在圖2中，繪制了3個水平C1＞C2＞Ca的濃度等值線。在以下小節中，將由方程式（10）具體分析污染混合區邊界（等濃度）曲線幾何特征參數的理論公式。

3.1 最大長度在式（10）中，令y=0，可以得到河流岸邊排放污染混合區最大長度Ls的理論公式:

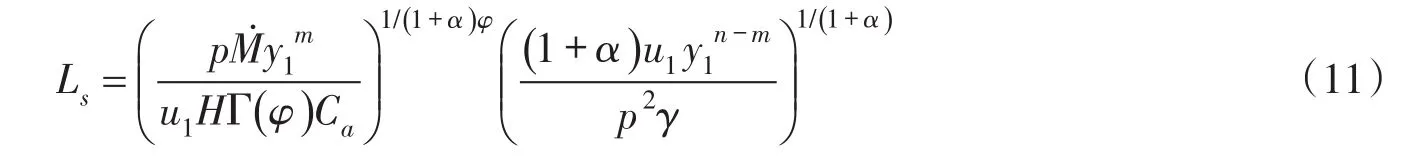
3.2 最大寬度和對應縱向坐標為了方便推導河流岸邊排放污染混合區最大寬度和最大寬度對應的縱向坐標位置，改寫式（10）為:

為了獲得等濃度線上橫向坐標y達到極大值點的坐標關系，給式（12）兩邊分別對x求導，并令dy/dx=0，整理得到:

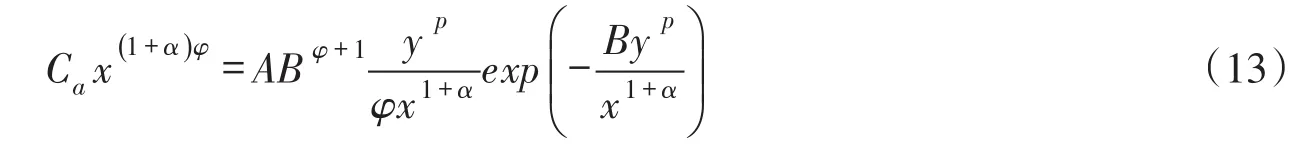
注意到，式（12）與式（13）的左邊相同，則右邊應該相等。據此，可以得到污染混合區最大寬度極值點的縱向坐標Lc和橫向坐標bs應滿足的關系式為:

將式（14）代入式（12），整理得到污染混合區最大寬度的理論公式為:

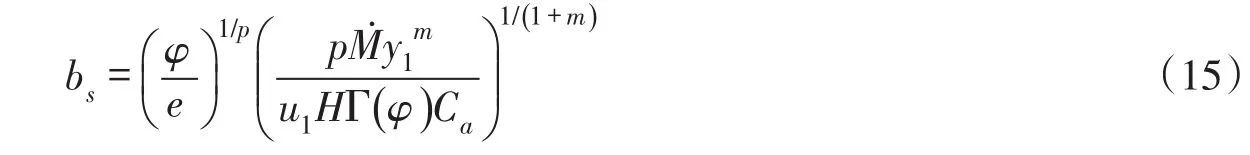
考慮到式（11），可以得到污染混合區最大寬度與最大長度的關系式為:

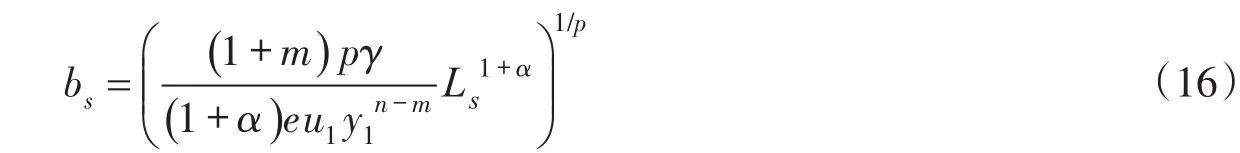
將式（16）代入式（14）化簡得到污染混合區最大寬度對應縱向坐標與最大長度的關系式為:

其中:q=1+α＞1。

3.3 邊界（等濃度）曲線方程在式（10）中，對坐標變量x除以Ls可以得到歸一化坐標（x/Ls），同時乘以式（11）右邊的最大長度表達式；對坐標變量y除以bs可以得到歸一化坐標（y/bs），同時乘以式（15）右邊的最大半寬度表達式，整理得到通用形式的河流岸邊排放污染混合區邊界曲線方程為:

或

值得注意的是，河流岸邊排放污染混合區歸一化坐標邊界的曲線方程僅是p（=2+m-n）和q的函數。其它參數（m，n，γ，α，y1，u1，H，Ca和˙）僅改變用于歸一化的兩個幾何特征參數Ls和bs。

3.4 面積和面積系數在縱向坐標x∈［0，Ls］上，對式（19）求定積分，可以推導河流岸邊排放的污染混合區面積S如下:

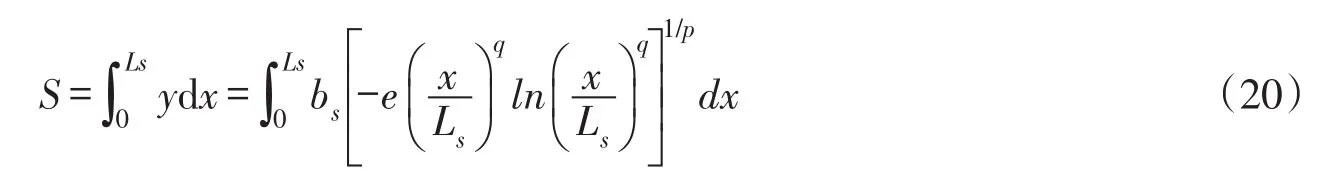
進行變量替換，令x/Ls=ζ，積分區間變為［0，1］，式（20）變為:

其中面積系數函數μ為:

（1）在特定條件下，面積系數的理論公式

當p=1時，式（22）改寫為:

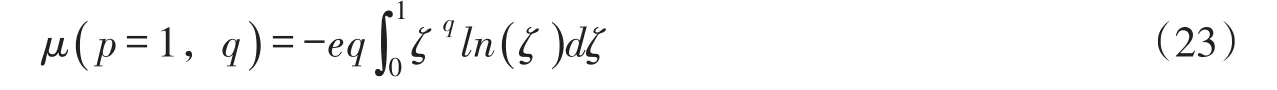
當p=2時，令η=ζ(2+q)/2，代入式（22）化簡得到:

（2）在其它條件下，面積系數的數值積分公式

除p=1和p=2以外，式（22）不存在直接積分公式。可以借助于梯形法求定積分的公式，由式（22）得到污染混合區面積系數的數值積分公式為:

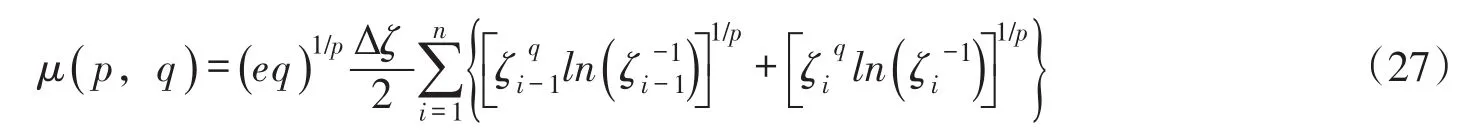
在式（27）中，將自變量ζ的積分區間［0，1］劃分為n（=1/Δζ）等分，每一等分的長度Δζ取1×10-4，一般就可以實現數值積分值與理論值的誤差絕對值小于1×10-4。若需進一步提高數值積分的精度，可以通過縮小等分長度或更換數值積分方法。

在河流流速和橫向擴散系數均為常數（p=2，q=1）、僅橫向擴散系數隨縱向坐標x呈指數變化（p=2，q=1+α）以及流速和橫向擴散系數為指數分布（p=2+m-n，q=1）條件下，式（24）或式（26）或式（27）可簡化為與相同條件下Wu等［27，29，31］給出的結果一致。

4 結果分析與討論

4.1 結果分析由式（18）和式（22）可以看出，河流岸邊排放污染混合區邊界歸一化曲線的形狀和面積系數，兩者都只是參數p（=2+m-n）和q（=1+α）的函數。下面分別繪制污染混合區邊界歸一化曲線分類圖譜和面積系數變化曲線族來做進一步分析。

首先，選擇參數p=2、p＜2（以p=1代表）、p＞2（以p=4代表）和q=1、q＞1（以q=3代表），針對（p，q）的6種組合情況，由式（18）分別繪制污染混合區邊界歸一化曲線，見圖3。圖中，標準型、Ⅰ型、Ⅱ型分別對應（p=2，q=1）、（p＜2，q=1）、（p＞2，q=1）情況，此時α=0，污染混合區最大寬度對應的歸一化縱向坐標Lc/Ls=1/e≈0.368；α-標準型、α-Ⅰ型、α-Ⅱ型分別對應（p=2，q＞1）、（p＜2，q＞1）、（p＞2，q＞1）情況，此時α＞0，污染混合區最大寬度對應的歸一化縱向坐標Lc/Ls＞0.368。

其次，選擇參數p=1.0，1.5，2.0，3.0，4.0和5.0，在參數q=1～5區間內取一系列值，采用式（24）或式（26）或式（27）分別計算污染混合區面積系數μ（p，q），給出以p為參數的面積系數μ（q）變化曲線族，見圖4。

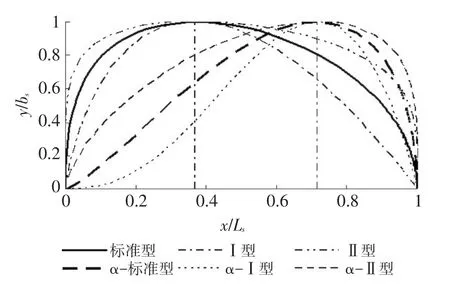
圖3 河流岸邊排放污染混合區邊界歸一化曲線分類圖譜

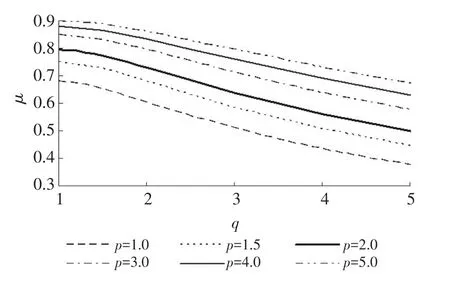
圖4 河流岸邊排放污染混合區面積系數變化曲線族

由圖3和繪制條件可知，當參數q不變，參數p變化時，污染混合區邊界歸一化曲線最大寬度對應的歸一化縱向坐標位置保持不變，只有污染混合區邊界歸一化曲線的形狀隨著參數p的增大，逐漸由尖瘦變為鈍肥；而當參數p不變，參數q變化時，污染混合區邊界歸一化曲線最大寬度對應的歸一化縱向坐標位置將隨著參數q的增大，沿著流向逐漸偏離原來位置，其形狀隨之發生變化。

由圖4可以看出，當參數p不變時，污染混合區的面積系數μ（q）為單調下降曲線，在q=1時的面積系數最大；當參數q不變時，污染混合區的面積系數隨著參數p的增大而增加，這一點與污染混合區邊界歸一化曲線形狀的分析結果一致。

通過以上分析，并注意到式（17）和式（18），可以得出的重要結論是:參數q值決定著污染混合區形狀最大寬度對應的歸一化縱向坐標位置，參數p值決定著污染混合區形狀的豐滿程度。

4.2 污染混合區的分類條件通過上述對河流岸邊排放污染混合區邊界歸一化曲線分類圖譜和面積系數變化曲線族的規律分析，發現:

當參數（p=2，q=1）時，對應河流流速和橫向擴散系數均為常數（m=n=0）以及流速和橫向擴散系數均服從橫向指數分布（滿足m=n）情況，這時的污染混合區形狀定義為標準型；當（p＜2，q=1）時，對應流速和橫向擴散系數橫向分布（滿足0＜m＜n）情況，定義為Ⅰ型；當（p＞2，q=1）時，對應流速和橫向擴散系數橫向分布（滿足m＞n＞0）情況，定義為Ⅱ型。

當（p=2，q＞1）時，對應流速為常數，橫向擴散系數僅隨縱向坐標x呈指數變化（滿足m=n=0、α＞0）以及流速和橫向擴散系數均服從橫向指數分布，同時橫向擴散系數又隨縱向坐標x呈指數變化（滿足m=n、α＞0）情況，定義為α-標準型；當（p＜2，q＞1）時，對應流速和橫向擴散系數分布（滿足0＜m＜n、α＞0）情況，定義為α-Ⅰ型；當（p＞2，q＞1）時，對應流速和橫向擴散系數分布（滿足m＞n＞0、α＞0）情況，定義為α-Ⅱ型。具體描述，詳見表1。

由表1可以看出，河流岸邊排放污染混合區的形狀與深度平均流速和橫向擴散系數變化的特性參數（p=2+m-n，q=1+α），具有一一對應的關系。在表1分類中，河流岸邊排放污染混合區的部分類型與已有研究特例的對應關系為:標準型與文獻［26-27］、α-標準型與文獻［29-30］、Ⅰ型和Ⅱ型與文獻［31］中的研究條件和結果分別對應一致。表1給出的河流岸邊排放污染混合區類別、形狀特征與分類條件是科學探究從特殊性到普遍性的系列研究成果。該成果全面科學系統地反映了用于表征河流深度平均流速和橫向擴散系數變化的特性參數（m，n和α）直接影響河流二維移流擴散污染物濃度分布規律和污染混合區幾何形狀特征的對應關系。

表1 河流岸邊排放污染混合區類別、形狀特征與分類條件

長期以來，尋找河流斷面平均橫向擴散系數（常數）的通常做法是根據橫向濃度分布與斷面平均水力學要素之間的關系，來建立基于常數的橫向擴散系數經驗公式。而忽視了對河流二維濃度分布和水力學要素的同步觀測與綜合分析，使得各自給出的橫向擴散系數經驗公式數量多，形式繁雜，各個公式的計算結果撲朔迷離［5］。其問題可能出在人們一直試圖采用常數橫向擴散系數來表征縱、橫向變化的河流橫向擴散系數。研究發現寬闊河流的中部深槽和遠岸地形變化，對排放岸附近污染混合區的污染物輸移擴散作用很小，因此在大江大河采用斷面平均橫向擴散系數是不合適的。

4.3 反問題：變橫向擴散系數的估算方法河流岸邊排放污染混合區邊界幾何特征尺度的理論公式和等濃度線方程，可以反向使用以便獲得變橫向擴散系數的具體表達式。該方法僅需要對岸邊污染混合區邊界曲線的宏觀幾何特征尺度和流速橫向分布進行測量，為從業者提供現場使用的有效方法，在大江大河中非常實用。

首先，在擬觀測的寬闊河流上，選擇一個穩定的岸邊排污口或排放點，在排水中以恒定速率均勻地投加無毒害有色熒光染料（如羅丹明B）溶液。岸邊污染混合區中的染料濃度與顏色的陰影成比例，即有同色度線表示等濃度線。需強調的是，當河岸傾角小于28°時，水面與深度平均濃度近似相等，水面濃度分布可作為污染混合區的確定依據［33］。這種要求通常在天然河流中很容易得到滿足。

其次，按照水文測量技術觀測河流中的流速橫向分布，采用式（1）擬合確定u1，y1和m的值。速度測量不需要覆蓋整個河流，只需要覆蓋形成污染混合區的近岸區域。

第三，采用無人機攝像裝置，從上空拍攝岸邊污染混合區的彩色圖像資料。經導入計算機、圖像篩選、坐標定位和圖像處理，初步讀取單條同色度線的最大長度Ls、最大寬度bs與對應的縱向坐標Lc。采用式（17）反推得到q的初值:

再對污染混合區邊界（等濃度）曲線的形狀，采用式（18）進行試錯法擬合比較，最終確定出一條與該單條同色度線吻合程度較高曲線的最大長度Ls、最大寬度bs和參數p、q值，從而可以求出正常數指數n=2+m-p和α=q-1。進而采用式（16）反推出正常數系數γ:

最后，將γ，α，y1和n代入式（2）得到變橫向擴散系數的具體表達式。

該方法的最大優點是無需測量排污量和濃度分布的具體數值，因為河流流速和橫向擴散系數變化形式決定了污染混合區的不同形狀，而排污量和濃度分布的具體數值主要是影響河流污染混合區的范圍大小。

5 實例

下面根據黃真理等［28］在長江三峽建水庫前庫區水環境現狀及水文水質污染負荷同步觀測中，給出的黃沙溪排污混合區平水期同步觀測資料，采用本文理論來估算該河段岸邊排放的變橫向擴散系數式（2）中的正常數參數和經驗公式。

黃沙溪排污混合區平水期CODCr現場觀測等值線與理論擬合曲線，參見圖5。圖中彩色渲染濃度部分摘自文獻［28］，3條濃度等值線均由式（18）擬合而得。表2給出了黃沙溪排污混合區平水期CODCr=9.85、10.00和10.81 mg/L相應的等值線最大長度、最大寬度和其對應縱向坐標的觀測值。經采用同一組參數（p，q）值和式（18）對圖5中的3條濃度等值線分別進行理論擬合。結果表明，當參數（p=1.50，q=1.65）時，對應表1中的α-Ⅰ型污染混合區，Lc/Ls=0.545，面積系數μ=0.713，3條濃度等值線的總體吻合程度最好，并給出了3條CODCr等值線的最大長度、最大寬度和其對應縱向坐標的理論擬合值，見表2。

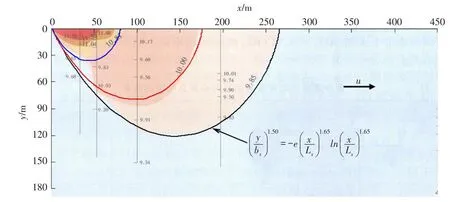
圖5 黃沙溪排污混合區平水期CODCr現場觀測等值線與理論擬合曲線

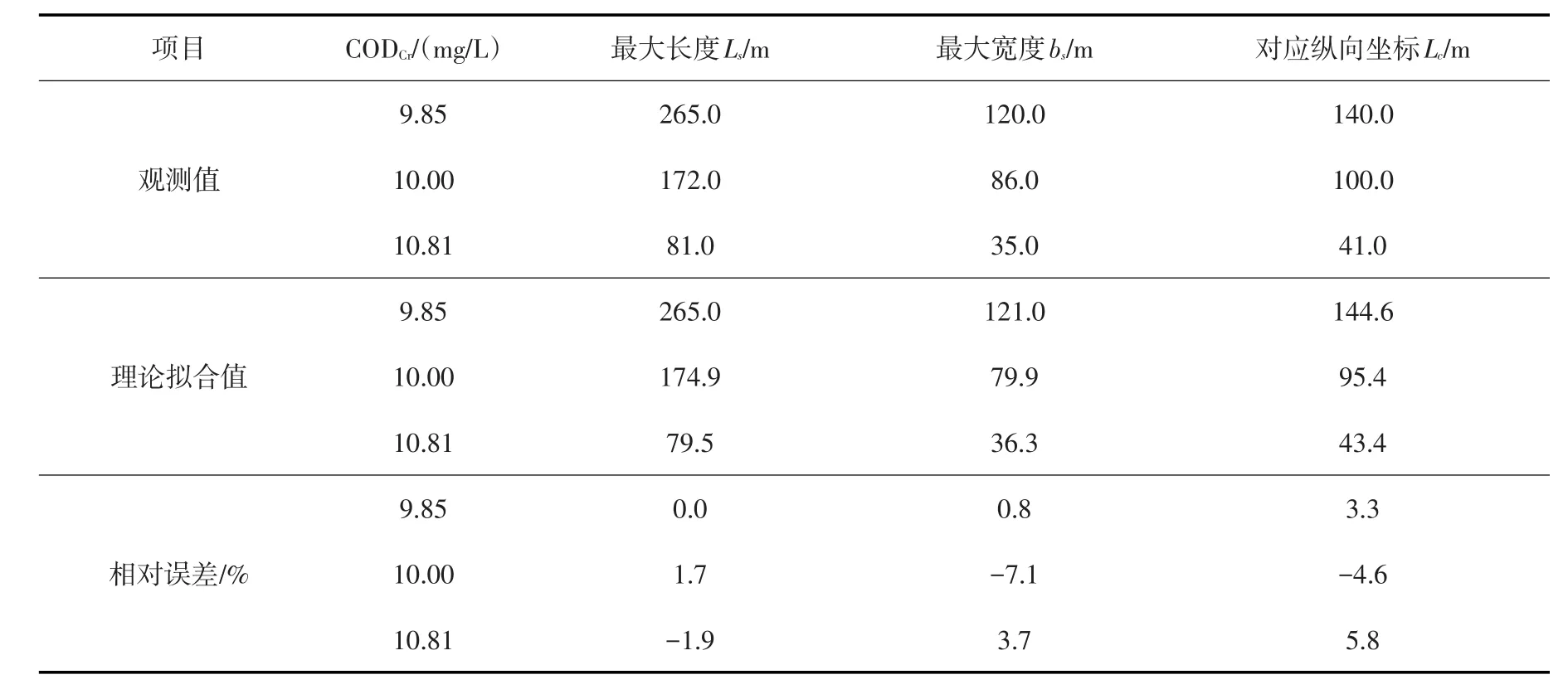
表2 黃沙溪排污混合區平水期CODCr等值線幾何特征參數

由表2可以看出，黃沙溪排污混合區平水期3條CODCr等值線最大長度、最大寬度和其對應縱向坐標的理論擬合值與觀測值的最大相對誤差絕對值分別為1.9%，7.1%和5.8%，結合圖5判斷兩者吻合良好。

基于2.1節中獲得的黃沙溪排污混合段平水期深度平均流速橫向分布式（1）中的有關參數:y1=150 m，u1=1.4 m/s，m=0.25，考慮到參數（p=1.50，q=1.65），求出正常數指數n=0.75和α=0.65。再根據黃沙溪排污混合區平水期3條CODCr等值線理論擬合的最大長度Ls、最大寬度bs和有關參數，采用式（29）分別計算出變橫向擴散系數中正常數系數，從而得到其平均值γ=5.96。最后，將γ，α，y1和n代入式（2）得到長江黃沙溪排污混合區平水期的變橫向擴散系數經驗公式為:

式中物理量采用國際單位制。

長江黃沙溪排污混合區平水期深度平均流速和橫向擴散系數的橫向分布指數m、n之和恰巧等于1，這與Li［32］在低層大氣擴散研究中，建議n值通常取為（1-m）一致。這是巧合還是有某種規律有待進一步深入研究。

需要說明的是:在野外水體中，雖然CODCr具有一定的降減能力，但根據文獻［26］給出的判別條件，當降解數De=KLs/U≤0.027時，可以忽略反應降解作用，按保守物質計算污染混合區范圍。如果取CODCr的較大降解系數K=0.4 d-1=4.63×10-6s-1，黃沙溪岸邊區域的平均流速U≈1.0 m/s，當CODCr=9.85 mg/L時的污染混合區最大長度Ls=265.0 m，由此計算得到降解數De=KLs/U=0.0012?0.027。所以，上述實例計算忽略反應降解作用是合理的。在文獻［28］中，對于黃沙溪排污混合區CODCr濃度場的驗證、污染混合區的模擬預測和實用化計算公式，同樣忽略了CODCr的降解作用。

6 結論

（1）這項研究在寬闊河流順直岸邊穩定點源條件下，考慮深度平均流速的橫向指數分布和橫向擴散系數的二維變化關系，基于變系數二維移流擴散方程，推導了污染物濃度分布解析解，提出了污染混合區最大長度、最大寬度和對應縱向坐標以及面積的理論公式。

（2）給出了污染混合區邊界歸一化曲線方程。表明河流岸邊排放污染混合區的形狀與深度平均流速和橫向擴散系數變化特性參數（p=2+m-n，q=1+α），具有一一對應的關系，提出了河流岸邊排放污染混合區的類別、形狀特征、分類條件和變橫向擴散系數的估算方法。

（3）實例表明，α-Ⅰ型污染混合區能夠較好地表征長江黃沙溪排污混合區平水期CODCr現場觀測等值線形狀。給出了黃沙溪深度平均流速和橫向擴散系數變化特性參數以及排污混合區平水期的變橫向擴散系數經驗公式。

（4）研究發現寬闊河流的中部深槽和遠岸地形變化，對排放岸附近污染混合區范圍的影響很小。因此，在大江大河考慮河流流速和橫向擴散系數的變化特性非常必要，應引起河流污染混合區幾何特征計算和水質建模工作者的高度重視。