擬合系數定常回歸法分析生物柴油運動黏度影響因素

隋 猛，李法社，申加旭

(1.冶金節能減排教育部工程研究中心，昆明 650093； 2.昆明理工大學冶金與能源工程學院，昆明 650093； 3.云南電力試驗研究院(集團)有限公司，昆明 650093)

隨著世界能源結構變化，為解決目前面臨的石油資源緊缺、環境污染和溫室效應三大難題以及資源的戰略儲備等原因，許多國家正積極開發可廣泛推廣應用、負作用小、污染少的綠色能源，其中生物柴油備受重視[1-2]。生物柴油是以植物油、微藻油、動物油脂及餐飲垃圾油等為原料油通過酯交換或熱化學工藝制備的可代替石化柴油的可再生液體燃料[3-4]。生物柴油具有可降解、無毒、燃燒低排放等優點。但生物柴油低溫流動性和氧化穩定性較差[5-6]。高黏度的生物柴油導致霧化效果差，燃燒效率低，發動機磨損等問題的出現。生物柴油在實際貯存運輸過程中，在氧、光、金屬離子等作用下，其中的不飽和酯類成分極易發生氧化反應生成醇、醛、有機酸、聚合物及沉淀物等[7]，導致生物柴油燃料的運動黏度增大。在低溫時，生物柴油易析出蠟狀晶體，堵塞發動機的管道和過濾器，影響發動機的正常啟動[8-9]。

影響生物柴油運動黏度的主要因素為溫度和組成成分，當生物柴油發生氧化時，會導致組成成分的變化而引起運動黏度發生改變。目前，國內外尚未有氧化程度與溫度對生物柴油運動黏度復合影響的相關報道和分析方法。本文以小桐子生物柴油為樣品進行了不同氧化程度和溫度對生物柴油運動黏度的影響研究，建立并利用擬合系數定常回歸法構建不同氧化程度和溫度雙因素對生物柴油運動黏度影響的數學模型，為優化生物柴油低溫流動性能提供理論支持。

1 材料與方法

1.1 試驗材料

小桐子生物柴油：采用循環氣相酯化-酯交換-甲醇蒸氣蒸餾精制工藝制備[10-11]，經去離子水多次洗滌，洗去甘油和堿性催化劑，再經真空旋轉蒸發器旋蒸、過濾得到的精制生物柴油，其理化性能指標見表1。

Classic威立雅生物試驗超純水儀，ELGA Labwater公司；Rancimat 873生物柴油氧化穩定性測定儀，瑞士萬通中國有限公司；SYD-265石油產品黏度試驗器；R-215真空旋轉蒸發器。

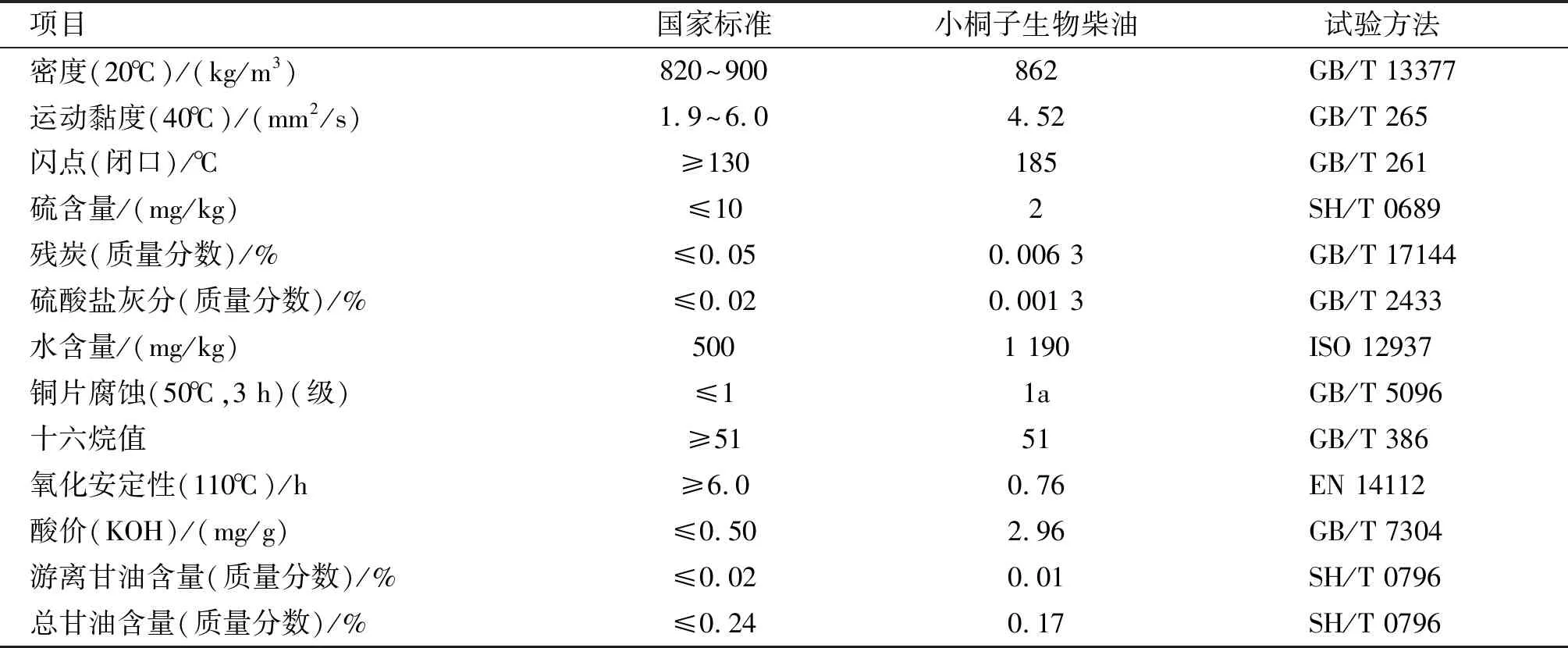
表1 生物柴油國家標準(GB/T 20828—2015)及小桐子生物柴油理化性能指標

1.2 試驗方法

本文旨在研究不同氧化程度和溫度對生物柴油運動黏度的影響，試驗采用加速氧化法制備不同氧化程度的小桐子生物柴油，并通過運動黏度試驗器測量不同溫度下的小桐子生物柴油運動黏度，試驗數據采用擬合系數定常回歸法進行處理及預測。

試驗利用Rancimat儀器測定生物柴油的氧化程度[12-15]。Rancimat測定法(EN 14112—2003)是將樣品在一定的溫度下連續通入空氣，不穩定的二次氧化產物就會被流動的空氣帶入另外1個裝有超純水的玻璃瓶內，使超純水的電導率隨之變化，用電極測定超純水電導率的變化，以電導率和時間作圖，得出電導率與時間的曲線。圖1為超純水電導率測試流程圖。在加速氧化過程中，隨著氧化時間延長，超純水電導率逐漸增加，圖2為電導率與氧化時間曲線。本文利用超純水電導率作為氧化程度指標。

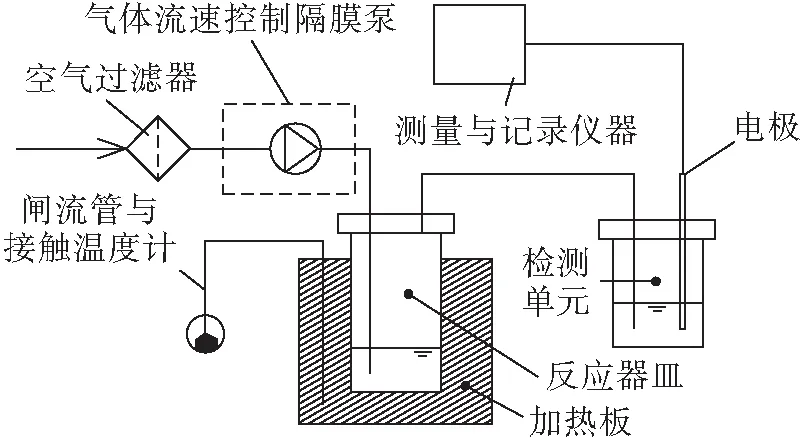
圖1 超純水電導率測試流程圖

生物柴油在氧化過程中溫度保持不變，待生物柴油氧化到一定電導率時，從氧化穩定性測定儀中取出氧化后的生物柴油，按GB/T 265—1988測試不同溫度下的運動黏度。

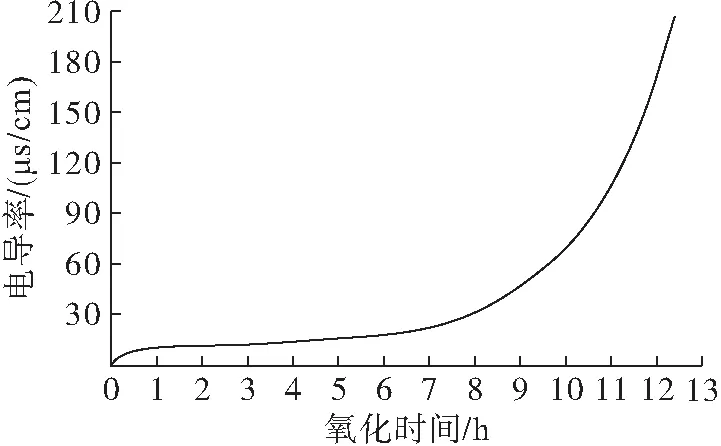
圖2 電導率與氧化時間曲線

1.3 擬合系數定常回歸法

1.3.1 擬合系數定常回歸法求解步驟

使用擬合系數定常回歸法求解曲面擬合方程時，先利用擬合系數定常法求解擬合函數形式，后利用散點圖與擬合函數，采用回歸法求出擬合曲面方程。求解過程主要分為以下幾步：第1步，畫出實驗數據三維散點圖。第2步，求解x/y為常數時，z=f(y)/z=f(x)的曲線函數形式。該步驟可查閱多種函數的曲線形狀確定或采用1stopt軟件計算。該步驟要求在x/y為任意常數時，z=f(y)/z=f(x)的函數形式不能發生改變，且不能出現因x/y取某一數值時y/x取任意值z都等于0的情況。第3步，構建擬合曲面方程形式z=f(x)+f(y)。第4步，利用origin/MATLAB進行數據擬合，求出擬合方程。

1.3.2 擬合系數定常回歸法求解曲面擬合方程

相對于平面擬合，工程試驗中獲得的雙因素試驗數據，在擬合后普遍為曲面方程。本小節舉例求解一階因變量的曲面方程。如表2所示，表中數據為z=x2+2x+2y2+1曲面方程中部分點。

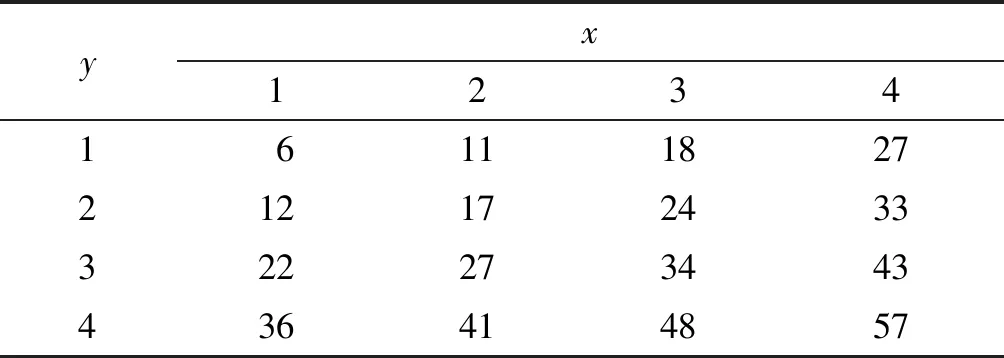
表2 方程z=x2+2x+2y2+1部分取值點

按照擬合系數定常回歸法求解步驟，首先畫出表2中數據的三維空間散點圖，如圖3所示。

圖3 三維散點圖

第2步，求解出當x/y為常數時，z=f(y)/z=f(x)經驗方程，如表3和表4所示。

表3 當x為常數時，z=f(y)經驗方程

表4 當y為常數時，z=f(x)經驗方程

根據擬合結果，得出x/y為常數時，z=f(y)/z=f(x)的曲線函數形式。根據表3，在x為常數時，曲面擬合方程在yoz面的投影函數形式為z=Ay2+B。根據表4，可以得出，在y為常數時，曲面擬合方程在xoz面的投影函數形式為z=Ax2+Bx+C。

第3步，求解曲面擬合方程形式為z=Ax2+Bx+Cy2+D。將表2數據帶入擬合方程，利用origin進行曲面擬合，求得曲面擬合方程為z=x2+2x+2y2+1，如圖4所示為origin擬合求解得到的曲面擬合結果空間圖形，擬合結果與原方程一致。結果顯示，建立的擬合系數定常法可以應用于求解曲面擬合方程。

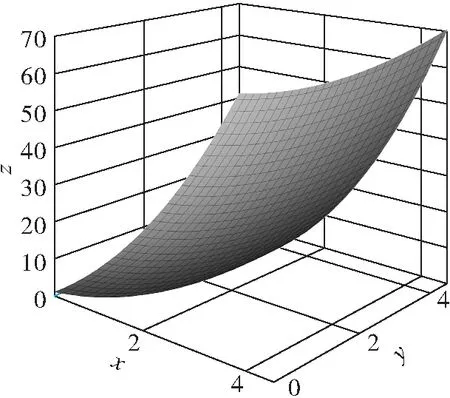
圖4 曲面擬合空間圖形

2 結果與分析

為了研究氧化程度和溫度對生物柴油運動黏度的復合作用，測量在不同氧化程度和溫度下的生物柴油運動黏度變化，求出擬合方程。采用擬合系數定常回歸法求解曲線擬合方程η=f(t)。利用方程η=eA+Bt+Ct2對生物柴油運動黏度優化，模型中η為運動黏度(mm2/s)，t為攝氏溫度(℃)。使用優化后的經驗公式處理不同氧化程度的小桐子生物柴油運動黏度，得到生物柴油的運動黏度與溫度的優化經驗方程如表5所示。

表5 小桐子生物柴油的運動黏度與溫度的經驗方程

根據表5可以得出，在電導率為常數時，η=f(t)函數形式確為η=eA+Bt+Ct2。結果顯示，在試驗溫度范圍內，生物柴油運動黏度隨溫度升高而逐漸降低。

采用線性擬合模型對試驗測量的不同電導率的小桐子生物柴油運動黏度進行線性擬合，求得經驗方程如表6所示。為了得出小桐子生物柴油運動黏度(η)與電導率(μ)的函數關系，分別對20、40、60、80℃時小桐子生物柴油運動黏度與電導率進行線性擬合。

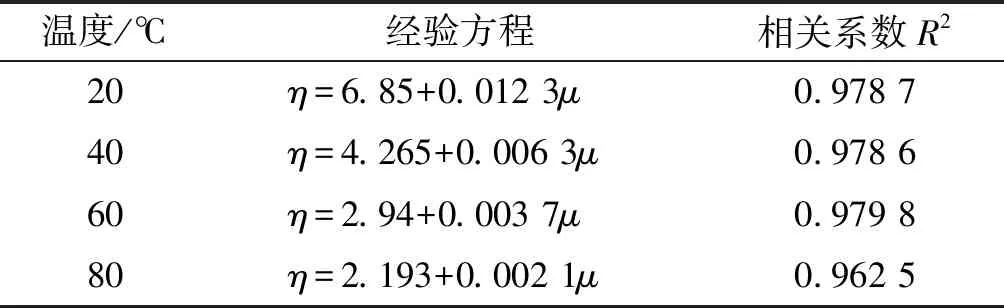
表6 生物柴油的運動黏度與電導率的經驗方程

根據表6可以得出,在溫度t為常數時，η=f(μ)的函數形式為η=A+Bμ。根據擬合系數定常回歸法曲面擬合方程函數形式求解方法z=f(x)+f(y)，得出不同氧化程度和溫度對生物柴油運動黏度的擬合方程形式z=A+Bx+eC+Dy+Ey2。求得經驗方程如表7所示。

表7 生物柴油運動黏度與氧化程度和溫度的經驗方程

作出小桐子生物柴油運動黏度三維散點圖如圖5所示，并和三維擬合曲面圖6進行對比分析。

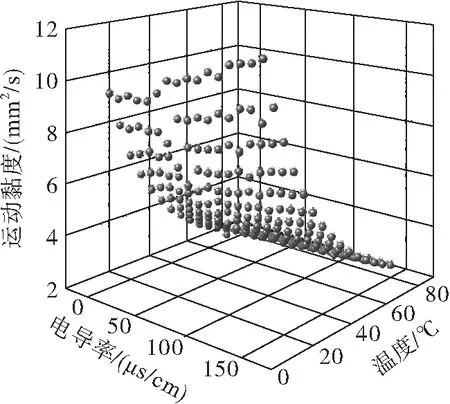
圖5 小桐子生物柴油運動黏度三維散點圖

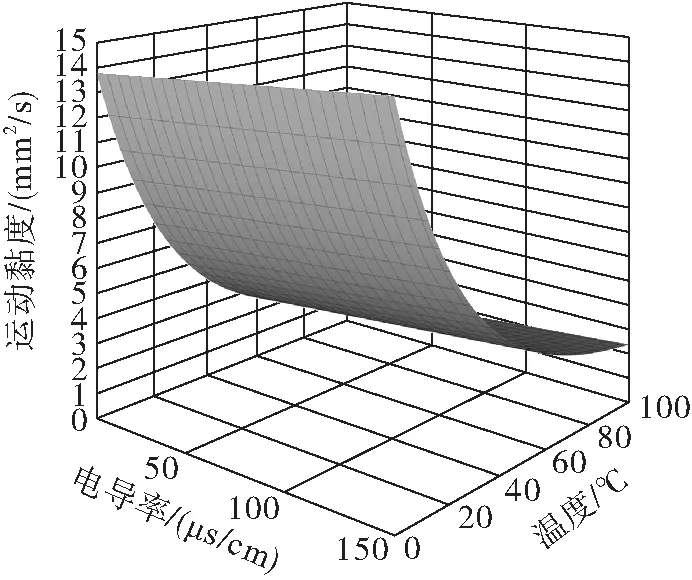
圖6 擬合曲面圖

經過圖5與圖6對比分析可知，通過擬合系數定常法構建不同氧化程度和溫度雙因素對生物柴油運動黏度影響的數學模型，相關系數較好，可以準確反映氧化程度和溫度對生物柴油運動黏度的復合影響關系，可以用于預測不同氧化程度和溫度下的生物柴油運動黏度。

3 結 論

(1)建立了擬合系數定常回歸法，經驗證分析證明，該方法利用試驗數據和三維散點圖可有效求解曲面擬合方程，求解的擬合方程在試驗區間內相關系數在0.99以上。可利用擬合系數定常回歸法求解部分實際問題中的雙因素復合影響試驗結果的擬合問題。

(2)在試驗溫度范圍內，生物柴油運動黏度隨溫度升高而逐漸降低。氧化前后的生物柴油運動黏度隨溫度的變化趨勢相同，用η=eA+Bt+Ct2回歸方程進行處理和數據預測，相關系數在0.99以上。

(3)小桐子生物柴油的運動黏度與電導率呈線性相關，用η=A+Bμ回歸方程進行數據處理。當溫度為20、40、60、80℃時，運動黏度與電導率的擬合直線相關系數R2分別為0.978 7、0.978 6、0.979 8、0.962 5。

(4)利用擬合系數定常回歸法構建不同氧化程度和溫度雙因素對生物柴油運動黏度影響的數學模型，得出生物柴油運動黏度與溫度和氧化程度的函數關系為η=0.194+0.007μ+e2.609-0.035t+0.000 1t2。