單噴頭水量分布函數擬合研究

仵 峰，徐 露，劉 煥，王富斌

(1.華北水利水電大學 水利學院，河南 鄭州 450046；2.河南省節水農業重點實驗室，河南 鄭州 450046)

噴灌均勻度是衡量噴頭水力性能和噴灌系統灌水質量的重要指標，通常采用噴灌均勻系數來表示，包括基于分布規律的均勻系數和基于空間水量分布函數的均勻系數兩種[1]。單噴頭的水量分布數據是計算組合噴灌均勻度的基礎[2-3]，通常采用量筒測量法獲取，再采用疊加法計算組合噴灌系統的均勻度。基于空間水量分布函數的均勻系數，將單噴頭水量分布看成一個具有特定形狀的連續系統，通過噴頭實測水量數據的變化趨勢和水量分布的連續性，利用已有降水深數據及其位置信息計算得出其他位置未知的降水深值，然后按照噴灌系統不同間距組合進行疊加，從而計算得出組合均勻度系數[4-5]。計算過程中水量與位置有關，目前表示單噴頭水量分布常用的方法包括插值函數和數學變換函數等。

函數法和插值法都是將噴頭的水量變化看成一個連續的整體，通過噴頭實測水量數據的變化趨勢，基于水量分布的連續性來描述兩個采樣點間的水量分布實際規律，繼而將實測的散點數據變成連續變化的曲線或曲面。插值法是根據已知的實測數據插出未測點位置的水深數據，得出網格型的水量分布矩陣便于計算均勻度。插值疊加法一直是研究的重點，常用的插值方法有平面插值法、距離插值法和兩次插值法等。韓文霆[6]研究的三次樣條兩次插值法是通過徑向和周向兩次插值得到水量分布平面上未知點的水深。函數法是對徑向實測水量散點數據分布的趨勢進行回歸分析，找到一個已知形式未知參數的連續曲線來最大限度地逼近這些點，從而將徑向噴灑水量與距離的關系表達出來，擬合后給出點的位置即可求出各個點的水深，從而計算得出均勻度。函數法研究的較少，朱旦生等[7]提出用傅里葉變換表示單噴頭水量分布，通過加權求和將射程內的函數擴展到射程外無限遠處，然后將所有噴頭水量分布函數疊加求和建立出任意點降水深的數學模型。但由于加權傅里葉函數太過復雜，一直以來并沒有推廣使用。

本文提出采用簡單函數對單噴頭水量分布進行擬合分析。實際上，噴頭水量分布中水量與位置兩個變量之間的關系大多為非線性的，這使得分析實際問題比較困難。故擬合時選擇非線性擬合模型，包括冪函數、指數函數和多項式函數等，其中多項式模型應用較多[8]。在實際應用中，數據點較多且變化復雜時，只采用一種多項式曲線函數擬合所有的數據點，可能難以取得較好的擬合效果，故本文嘗試根據噴頭水量分布形狀的不同采用連續多項式函數和分段函數方法進行擬合[9]，以便于更精準地描述水量分布趨勢，為均勻度計算提供更好的疊加基礎。

1 材料與方法

1.1 噴頭試驗裝置

單噴頭水量分布常采用量筒測量法獲取，量筒布置方法分為徑向布置和網格型布置[10-11]。試驗選用量筒徑向布置方式。單噴頭試驗在華北水利水電大學河南省節水農業重點實驗室進行，試驗場地地勢平整開闊，最大坡度小于2%。試驗選用噴頭為PY1-20、Nelson R33、FY RB-471、GJYA-2、ZY-1和中原12y。各噴頭試驗條件如表1所示。

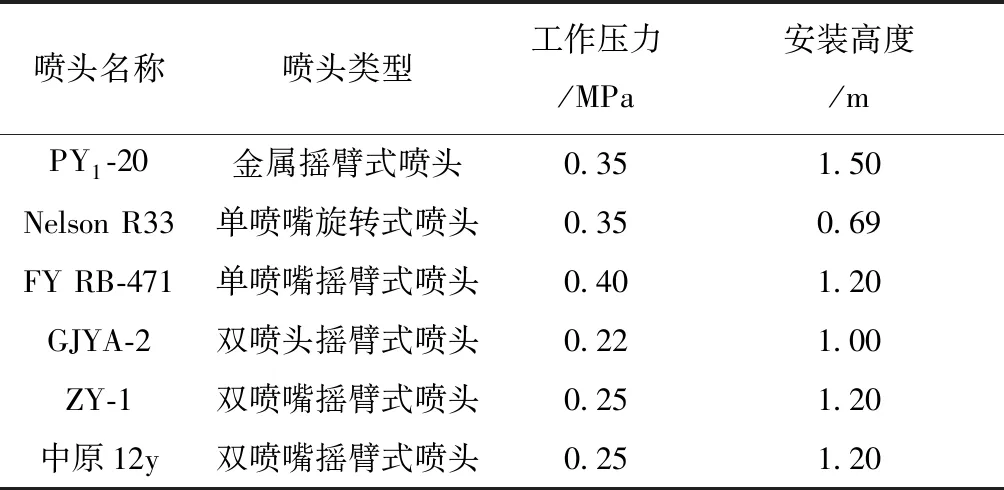
表1 噴頭試驗條件

試驗時將噴頭安裝在垂直固定的三腳支架上，噴頭壓力由壓力表讀出，流量通過流量計測出。試驗中量筒采用徑向布置方式，以噴頭為中心，沿噴頭噴灑方向量筒呈射線分布，每條射線之間的夾角均為90°，共4條，每條射線上間隔均勻地布置量筒，一直延續到噴射半徑之外。在噴頭達到穩定運行狀態后，每工作1 h進行水量分布試驗數據測量。試驗系統示意圖見圖1。

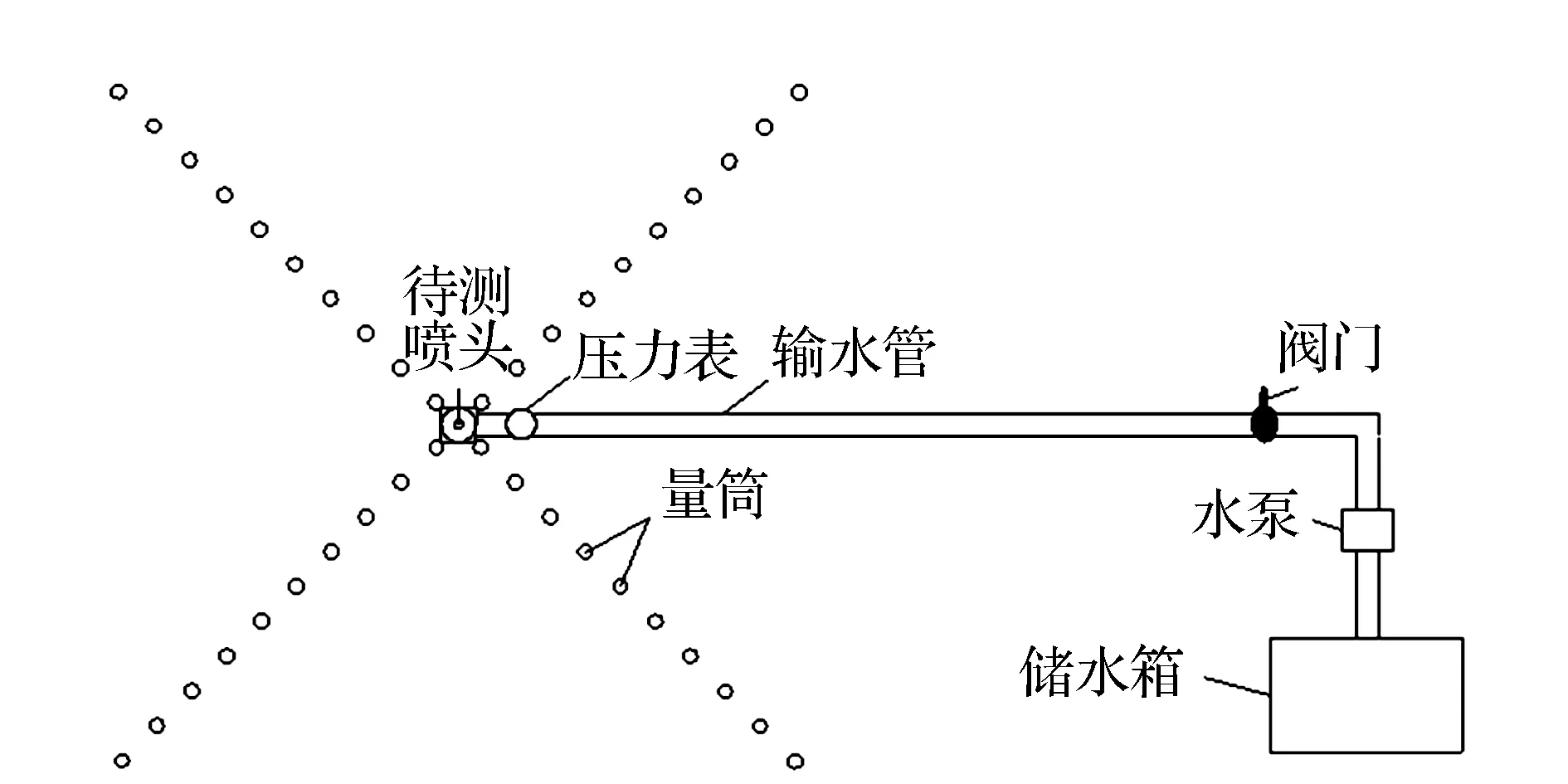
圖1 試驗系統示意

1.2 噴灌均勻系數計算

噴灌均勻系數采用克里斯琴森均勻系數Cu來表示[12]，其噴頭組合均勻度計算公式如式(1)所示。

(1)

在實際工作系統中噴頭總是以組合的形式進行噴灑運行的，目前測試噴頭組合均勻度最常用的方法是利用單噴頭水量分布數據，通過一定的計算方法轉化為多噴頭組合的數據，然后利用克里斯琴森均勻度計算公式進行計算。采用函數疊加法計算均勻度時，首先根據實測水深數據擬合出水量分布函數曲線，再由函數關系計算均勻度計算點處的未知水深，根據噴頭不同的組合方式和組合間距將水量進行疊加，繼而帶入公式計算求得組合均勻系數。所以在采用函數疊加法計算組合均勻度時，單噴頭水量函數擬合的準確度非常重要，擬合時需要根據不同噴頭水量分布的特點選擇適合的函數進行。

試驗測量得到的數據通過SPSS進行擬合分析。

2 結果與分析

2.1 單噴頭水量分布

以PY1-20型噴頭為例，表2為PY1-20型單噴頭在試驗工作壓力為350 kPa、風速0.3 m/s時，噴灑試驗中徑向布置的量筒的實測降水深數據。表2中第1列數據為距離噴頭1 m處的降水深，近似代替噴頭所在位置的降水深，其余量筒的間距均為2 m，一直延續到噴灑半徑外。

從表2可以看出，由于室外不是完全無風狀態，所以測得的4條射線數據有所差異，但差異較小，故取其水量數據的均值作為擬合依據[13]。圖2為根據實測數據做出的各類噴頭的徑向水量分布散點圖，噴頭測試時間均為1 h。

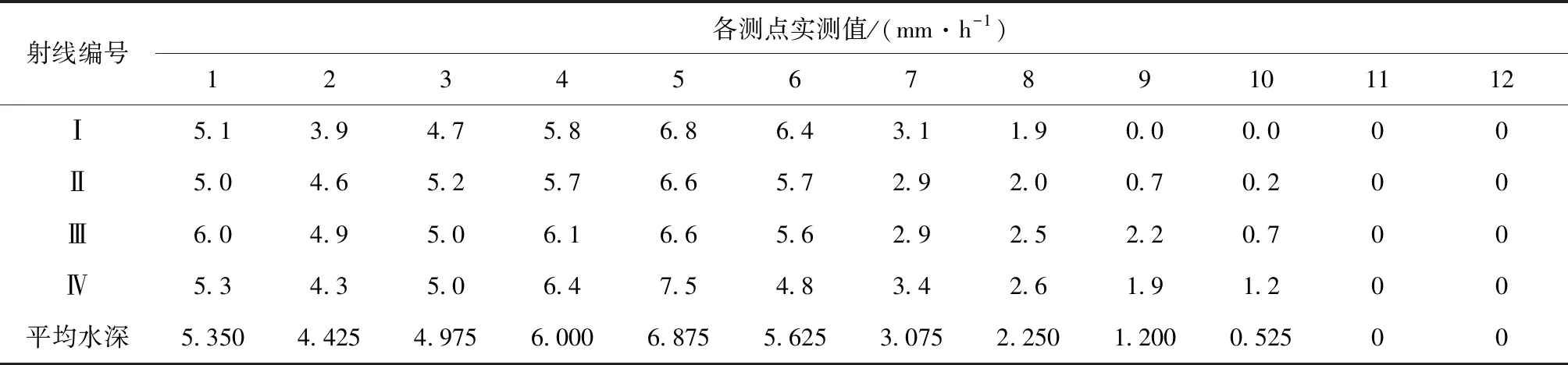
表2 單噴頭(PY1-20)水量分布實測數據

圖2 不同類型噴頭實測徑向水量分布散點圖

由圖2可以看出，單噴頭水量分布形態可分為單峰、雙峰、下降式和平緩式等。PY1-20型噴頭水量分布整體呈現單峰的形態，由噴頭往遠處呈現先減小再增大后減小的趨勢，徑向水量分布中存在1個低點1個高點。FY RB-471噴頭的徑向水量分布整體呈單峰式，其趨勢為先增大后減小，變化連續，且變化幅度大，變化區間內有1個高點。ZY-1噴頭的徑向水量分布整體呈下降的趨勢，噴頭遠處有一個小幅度的水量回升，整個噴灑區間內有1個拐點、1個低點和1個高點。中原12y徑向水量分布區間內有升有降，呈現雙峰的形態，區間內有2個高點和1個低點。GJYA-2噴頭的徑向水量分布整體呈一個先下降后平緩的趨勢，噴頭近處的降水量大，其余位置較為平均。Nelson R33噴頭的徑向水量分布特征整體趨勢為先減小后增大再減小，中間變化細微有增有減，變化略微復雜的單峰，區間內有1個低點和1個高點。

由圖2可知，噴頭水量分布中距離與水深之間不是簡單的線性關系，FY RB-471、ZY-1和GJYA-2噴頭，水量分布變化較為簡單，區間內只有1個高點或是連續下降的趨勢，采用連續多項式函數擬合即可達到較高精度。對于其余3種噴頭，其水量分布區間內有多個高點和低點，采用連續多項式函數擬合，可能造成精度較低或次數過高。為了得到更好的擬合效果，選用分段函數進行擬合。本文采用SPSS進行輔助擬合，以FY RB-471和中原12y為例，分別進行連續函數和分段函數的擬合。

2.2 單噴頭徑向水量分布回歸分析

2.2.1 FY RB-471噴頭水量分布擬合

以FY RB-471噴頭實測數據為基礎，采用SPSS軟件進行非線性回歸分析，令置信度為95%，擬合得到距離與水量之間的回歸曲線函數為：

y=-0.010x5+0.196x4-1.144x3+1.451x2+

3.319x+1.390

(2)

圖3為擬合后的水量分布曲線圖，由圖3可以看出該曲線對散點圖趨勢擬合較好。

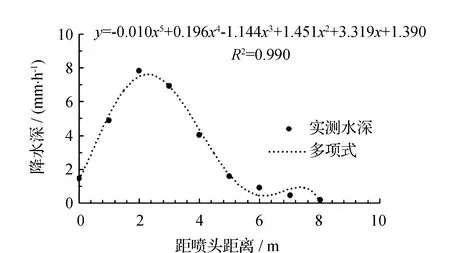
圖3 FY RB-471噴頭水量分布曲線

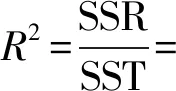
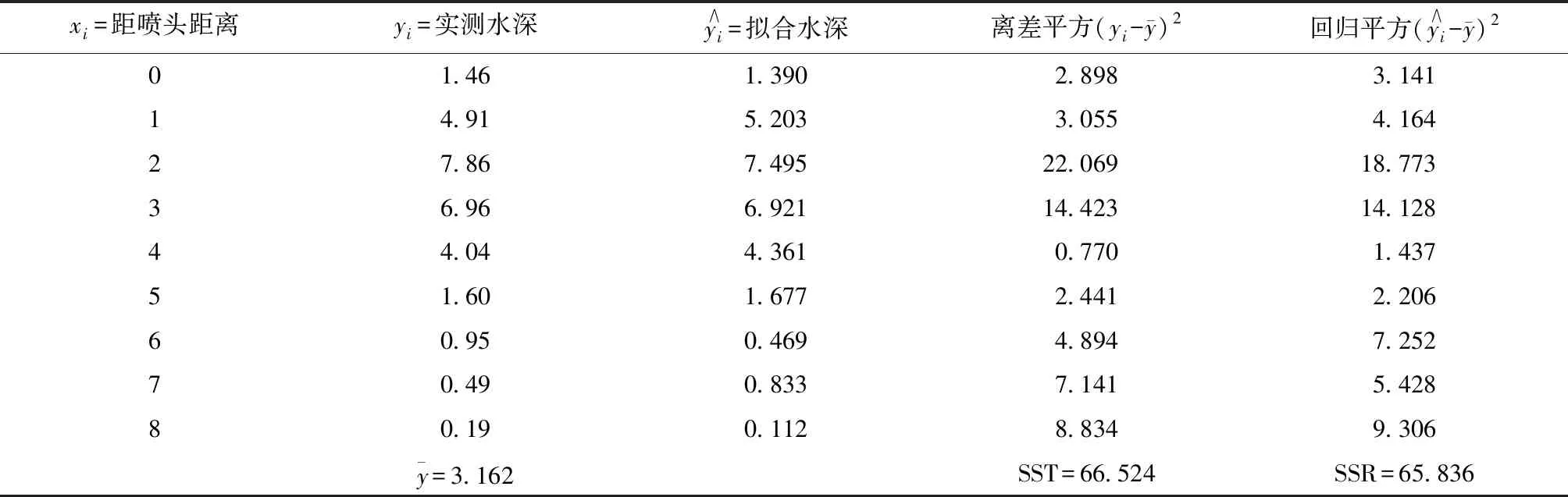
表3 FY RB-471噴頭水量分布SST和SSR的計算

2.2.2 中原12y噴頭水量分布擬合

先對其進行連續多項式函數的擬合，以中原12y噴頭實測數據為基礎，采用SPSS軟件進行非線性回歸分析，令置信度為95%，計算得到距離與水量之間的回歸曲線函數如下:

y=-3×10-5x5+0.001x4-0.014x3+

0.155x2-1.116x+5.995

(3)

計算得出其判定系數R2=0.776。擬合后的水量分布曲線見圖4。

由圖4(a)可以看出，采用連續多項式擬合得到的曲線與實際水深數據偏差較大，所以采用分段曲線擬合，以水量分布的轉折點為分界點，為了保證數據的連續性，以前一組數據的結尾數據為后一組數據的起始數據[15]。

經過對比，選擇中原12y噴頭的第7和第12個數據點為分界點，將其分為3段進行擬合。采用SPSS進行非線性回歸，擬合后第1段和第2段為3次曲線，表達式為：

y1=-0.044x3+0.6734x2-3.172x+7.924

(4)

y2=-0.005x3+0.388x2-5.828x+27.234

(5)

第3段數據經擬合后得到一個4次曲線，其表達式為：

y3=0.046x4-2.727x3+59.51x2-

571.46x+2043.2

(6)

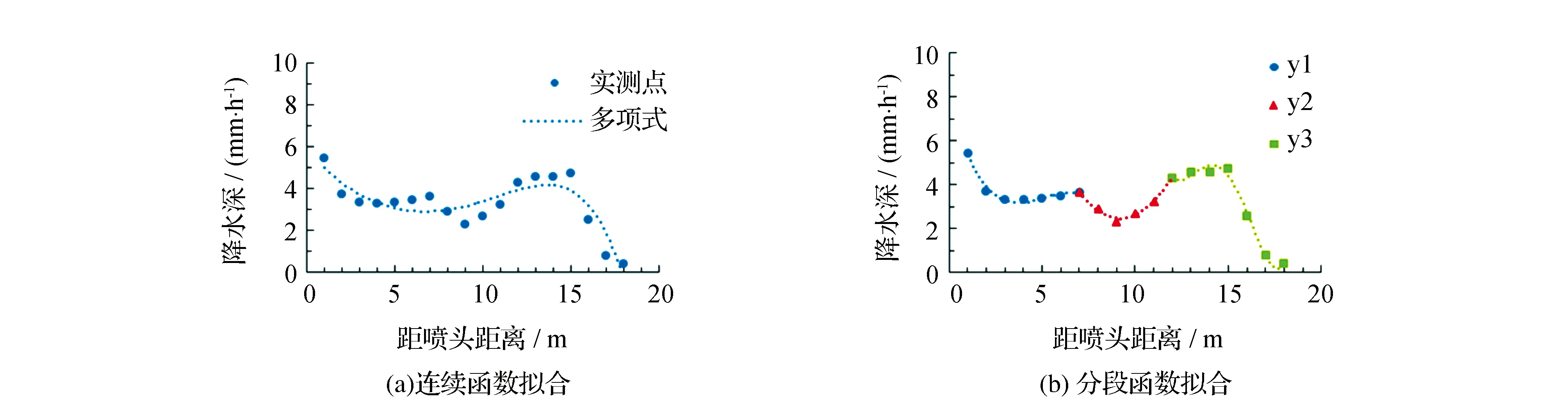
圖4 中原12y水量分布擬合曲線

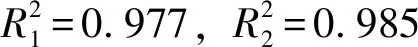
2.3 其他各個噴頭的水量分布曲線

同種方法對PY1-20等4種噴頭分別進行擬合。從PY1-20和Nelson R33噴頭的擬合結果可以看出，雖然分段函數擬合后次數降低，且精度提高了一些，但連續多項式函數擬合時曲線已經達到較好效果，且選用分段之后對于求均勻度的疊加計算也會相對復雜，所以擬合時二者精度相差不大的情況下，優先選擇連續多項式擬合。結果見圖5。

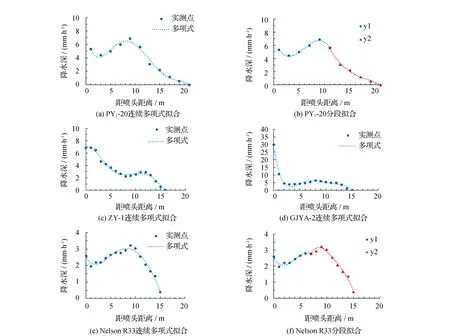
圖5 不同噴頭水量分布擬合曲線

ZY-1噴頭和GJYA-2噴頭的水量分布曲線均為五次多項式，判定系數R2分別為0.972和0.982。由判定系數和圖5可以看出，該曲線可以很好的表征水量分布趨勢，不需要再進行分段擬合。

由此可知，為了擬合精度的需要，進行擬合時不同類型噴頭根據水量分布的特點應選擇不同類型的曲線。如中原12y的散點圖比較復雜，從擬合結果看采用連續多項式曲線函數擬合后次數高且難以取得較好的擬合精度和效果，為了有效解決這個問題，選用分段曲線擬合。又如ZY-1和GJYA-2雖然數據較多，但其變化單一水量分布區間內沒有多個轉折點，采用連續多項式函數即可達到精度要求。

3 結 論

單噴頭水量分布是計算組合噴灌均勻度的基礎，實際求均勻度的疊加計算過程中需要先對單噴頭水量分布進行計算。本文通過單噴頭噴灑試驗測得6個不同型號噴頭的水量分布數據后，根據各個噴頭水量分布特點的不同進行曲線擬合，經對比得出以下結論。

(1)不同類型噴頭的水量分布形態不同，由試驗測得水量分布散點圖可以總結出，單噴頭水量分布根據總體形態可分為單峰、雙峰、下降式和平緩式等。

(2)對單噴頭水量分布擬合時采用非線性回歸分析，一般選用連續多項式函數和分段函數對噴頭進行擬合。通過對比6種不同類型噴頭擬合結果得出，進行擬合時要根據噴頭水量分布特點的不同選擇不同類型的曲線。對于類似GJYA-2和FY RB-471變化平緩單一的單峰或平緩下降式噴頭采用連續多項式函數擬合即可達到擬合效果。對中原12y等水量分布比較復雜的雙峰噴頭，進行水量分布擬合時，需采用分段擬合來提高擬合精度和效果。

(3)采用連續函數和分段函數擬合同一噴頭水量分布時，當二者得出結果精度相差不大的情況下優先選擇連續多項式擬合。采用分段函數擬合時函數式次數較低且精度更高，但分段函數用于組合均勻度疊加計算時比采用連續多項式函數疊加更為復雜。單個多項式函數擬合下精度比分段函數略低，但也足以較好地描述水量分布，且為組合噴灌均勻度的計算提供更為簡便的疊加基礎。