琢磨讀之，通融行之

許貽亮

“用教材教而不是教教材”是理性使用教材的一般性說法。但是，怎樣使用教材才算得上是用好教材呢？一線教師常存在著諸多困惑，也常見諸多不甚合理的做法。一方面是對于“教材”琢磨得不夠，折射出“讀”的問題;另一方面是對于“教學”思考得不深，折射出“行”的問題。筆者以為，“讀”可取的態度應該是“琢磨”，而“行”可取的策略可以是“通融”。其根本指向的目標是：關注學生的數學思維發展，讓學生“通過數學學會思考”。具體操作如何進行，本文結合課例具體展開探討。

一、琢磨教材，在“通透”中前行

要用好教材，首先就要琢磨教材，認真、仔細、深入地讀懂教材。這其中，包括表層內容，如課題、情境、問題串、旁白、習題等，也包括深層內容，如內涵、外延、邏輯、意圖等。既要讀出教材科學、合理的內容與形式，也要善于思考，提出教材因篇幅、地域、時間變遷等而產生的不適切內容。這樣讀，才能既走進教材又走出教材，也才能在教學實踐中“通透”地前行。

例如，教學北師大版四下“探索與發現：三角形邊的關系”。分析教材中的3個問題串：第一個問題引導學生通過操作，發現問題（有的能擺成，有的擺不成）;第二個問題是引導學生思考其中的道理，發現三邊之間的初步規律（較短的兩根小棒的長度之和大于長的那根小棒）;第三個問題則用一一列舉的方式，讓學生從不完善到完善、從特殊到一般地歸納出三邊間的關系。

教材的編排從操作入手，逐步過渡到觀察、分析、計算、歸納等環節，符合學生認知的一般規律。但反復琢磨，可讀出如下問題：其一，如果擺不成三角形，那么這3根小棒就不是三角形的邊，可以借用它們來探究三角形的三邊關系嗎？其二，兩根較短的小棒長度之和剛好等于較長小棒的長度，用于操作的話會很“順利”還是很“意外”？其三，三角形兩邊之和大于第三邊，是通過擺出來發現的嗎？其數學本質是“加法的不等式”嗎？

顯然，本課的教學內容涉及兩個方面：其一是，基于兩點之間直線段最短而發現“三角形任意兩邊之和大于第三邊”;其二是，基于關系，對所給3根小棒是否能圍成三角形做出判斷。一個是理解，一個是應用。兩個層次一先一后，相銜而行。而教材編排上，這個次序顯然是顛倒了，先“應用”后“關系”，邏輯上不通透、不合理。

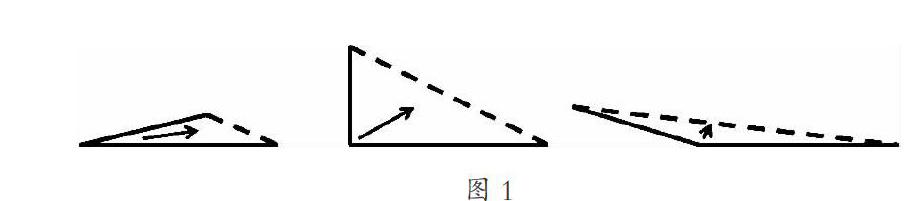
基于邏輯通透的思考，筆者對本節課進行如下設計：①出示小明家、公園、學校的路線圖（剛好圍成一個三角形）。以“可以怎么走”為核心問題，讓學生直觀地感知從小明家去公園或學校，或從學校去公園等，都是“直著走”比“繞著走”近。再用數學式子表示出來：A+B>C、A+C>B、B+C>A。從而發現三角形三邊的關系：“三角形的任意兩邊之和大于第三邊。”②要選3根小棒圍成一個三角形，你會怎么選？（提供：6厘米、8厘米、9厘米、11厘米、13厘米、15厘米的小棒各1根）讓學生先說出選擇的小棒，再進行實際操作驗證;學生應用規律實現應用的泛化，借助操作理解6+8<15圍不成三角形的道理，借助課件理解6+9=15也圍不成三角形的道理，再進行練習強化。③提供兩根小棒（9厘米和15厘米），讓學生思考第三根最長幾厘米？最短幾厘米？（取整厘米數）緊接著，讓學生透過現象看本質：兩根同樣的小棒，第三根小棒的長度為什么會不一樣呢？從而發現：小角對應著短邊，大角對應著長邊。（如圖1）讓學生不僅知道第三邊的結果，更知道第三邊長度變化的緣由，讓學生獲得頓悟的愉悅。

這樣教學，既基于教材，又不拘泥于教材。教師思考上的通透，決定著學生數學思維的通透，最終以“序”為線，促進學生數學思維發展。一方面，遵循認知邏輯上的序：先理解、再應用。另一方面，遵循學生認知特點的序：先整體、后微觀。同時，在教學中放大、突顯數形結合、猜測驗證、觀察明理等環節，使學生的歸納思維、求證思維、辯證思維等得到確實的發展。

二、琢磨學生，在“變通”中深刻

教學，教是起點端，學是終點端。教學出現問題，常常是教師對于學生琢磨得不夠、不透，不能走進學生的內心世界。要讀懂學生的現有起點、學習需求、內在心理等，不墨守成規，才能變通設計，從而讓學生感受數學的魅力，深化數學思維。

例如，教學北師大版五下“郵票的張數”一課。對課例情境“家中姐弟集郵”（姐弟共有180張郵票，姐姐的郵票張數是弟弟的3倍），以及4個問題串進行分析：前3個問題是可以歸為一組，從問題和方法指導入手，讓學生經歷分析數量關系到列方程解答的全過程。第4個問題其實是這一過程的拓展應用（從和倍問題到和差問題）。

從學生的起點來看，學生已學習過用字母表示數、等量關系、方程、解方程等初步的代數內容，并且也會用方程解決簡單的數學問題。本課中未知數從1個增加到2個，且指定用方程解答，是要讓學生體驗化逆為順的思維特點，增強用方程解決問題的意識和能力。但是，在不強求用方程解答的情況下，絕大多數的學生采用的是算術解還是方程解？甚至在強求用方程解答的情況下（如考試中），仍有部分學生采取算術解的方式，又是為什么？折射出來的學習心理、學習需求等需要我們琢磨。對于和倍問題、差倍問題等兩個未知數的數學問題，學生由于先前學習經驗影響（畫圖、平均分等），算術思維仍是潛意識的第一反應，代數思維仍是一種強制性的指令反應。同時，對于用方程解的過程的繁復（先解設，再解答等），學生常下意識地排斥。簡言之，學生并不像我們期待的那樣愛上方程解，教學目標談何達成？

基于對學生學情的琢磨，筆者對本節課進行如下設計：①出示主題圖，讓學生整理出其中的等量關系：姐姐的郵票張數+弟弟的郵票張數=180張。問：“那姐弟各有郵票多少張？”讓學生明白，答案不確定。②逐步出示中間的條件信息，讓學生用自己喜歡的方式列式解答（算術解、方程解都是可以的）。a.姐姐的郵票張數是弟弟的3倍;b.姐姐的郵票張數比弟弟多40張;c.姐姐的郵票張數比弟弟的3倍少20張。3個條件有序遞進，從和倍問題、和差問題發展到非整數倍的數學問題，在重復中讓學生經歷從不用方程到用方程也可以，再到方程很好用的過程，深刻感受方程的特點和價值，體會用方程解的結構統一性、思維簡明性。③讓學生梳理小結：方程，好嗎？強化學生對于方程的認知。④利用變式練習讓學生形成理性策略：什么時候用方程解，什么時候不用方程解？

善于變通的教學，培養善于變通的學生，使學生數學思維更為深刻：其一，強化列方程而弱化解方程。突出意識優先，讓學生先行確立“我想用方程解”“我會用方程解”的意識。課堂更聚焦，不陷入零散的求解計算中。其二，強化解法自由而弱化指定方程。變說教為自悟，“用方程解”不是教師單方面強求，而是學生在嘗試中不知不覺地自我確立。由此，學生的方程思維、優化思維、靈活思維等得到了確實的發展。

三、琢磨結構，在“融匯”中完善

教材和教學都是有結構的，起承轉合中自有內在的脈絡。這些結構，如果只讀一課教材而不放眼整套教材是難以琢磨出來的，如果只是讀教材的表面知識、技能而不是深究數學本質也是難以琢磨出來的。換句話說，要把知識的前世、今生、未來放在全局中來看，要把課堂教學的起與落、放與收等放在結構中考量，用“融匯”給學生以合力，推動學生數學思維的發展。

例如，教學北師大版四下“買文具”一課。分析教材中的3個問題串及生活情境“買文具”，問題1與2解決的是一位小數乘整數的算理和算法，突出學生利用原有知識經驗解決生活問題的策略，滲透轉化、數形結合等數學思想，發現整數乘法與今天所學內容之間的“結構一致性”。問題3，是知識的泛化應用，從0？郾2乘幾到0？郾4乘幾，從積為純小數到積為帶小數，從而讓學生在應用中進一步理解算法、熟練算法。

可以看出，本課教材內容安排已經具有一定的結構性。但是仔細琢磨，這一結構尚有一些欠缺：其一，小數乘整數的算理結構僅是轉化為小數加法，還不夠突顯，沒有和以往學習乘法的認知結構緊密地結合起來;其二，小數乘整數的應用結構僅是買文具，局限于購物，沒有更廣泛、更靈活地解決生活問題;其三，小數乘整數的承載結構僅是純小數乘整數，還比較單一，是否應該適當涉及帶小數乘整數的內容;其四，小數乘整數的算法結構僅靠學生感悟，還比較零散，沒有進行算法的歸納與整理，不利于學生熟練技能、形成能力、發展思維。

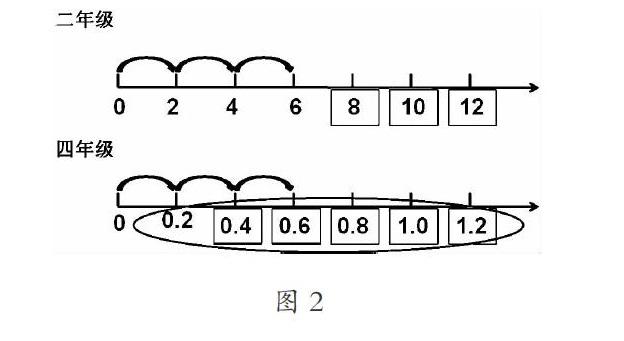
基于對結構的思考，筆者對本課進行如下設計：①回顧，喚醒經驗。用“你會計算嗎”直擊學生認知心理，把前面學習的相關計算內容進行一次簡要梳理，也為課末的拓展埋下伏筆，使學生在一開始就對小數乘法有一個全景式認知。②遷移，利用經驗。從買橡皮到買鉛筆和尺子，從純小數乘整數到帶小數乘整數，讓學生理解算法、熟悉算法。可以把二年級學習乘法時用的數線模型納入本課教學，讓學生在數一數中，進一步體會乘法的意義，形成一致性的認知結構。（如圖2）③應用，活用經驗。以0.5乘3為載體，從有單位的量到無單位的數，從一種列式到兩種列式（滲透乘法交換律），從買文具的生活場景到“還可以解決什么樣的生活問題”，從一位小數乘整數到兩位小數乘整數，從熟悉算法到概括算法，使學生感悟到小數乘整數結構應用的廣泛性及方法的可遷移性。④拓展、內化經驗。以0？郾3×0？郾2引發學生思考，并促進學生進一步拓展：后續還將學習什么？從而使今天的學習、未來的學習形成一個有機的、更完善的數學認知結構。

良性結構的教學，成就有張力結構的學生。把有聯系的內容聯通起來，把過去、現在和未來融合起來，從原有的教材出發，向四面八方展開搜索、鏈接、整合，體現教學的完整性、豐富性、層次性，使學生在化歸思維、求異思維、類比思維等方面獲得發展。

琢磨從教材、學生、結構入手，以通透、變通、融匯等通融策略為著力點，可以有力地推動學生多種數學思維的確實發展，也推動教師在教學研究、教學行動上的不斷深入，最終實現教學相長的和諧統一。

（作者單位：福建省晉江市第二實驗小學）