一種基于近似MMSE的迭代檢測算法

張榮升，許崇斌，王昕

(復旦大學 信息科學與工程學院，上海 200433)

0 引言

隨著信息技術的發展與應用，在我們的生活中產生的數據量也逐漸增多，同時對數據傳輸速率的要求也越來越高，所以發展第五代通信系統(5G)成為必然。而大規模輸入輸出(Massive MIMO)是5G的重要技術[1], 大規模MIMO中，一個基站(Base Station, BS)有很多天線并服務于很多單天線用戶。

在MIMO的符號檢測中，通常我們可以通過接收機(如MMSE)來獲得較好的性能，但是由于MMSE的求解中需要用到矩陣求逆，其復雜度較高。所以為了減少MMSE檢測的復雜度，在[2]-[5]參考文獻中提出了一種近似的MMSE(AMMSE)求解方法，主要原理是基于Neunann級數近似。但在大規模MIMO中用戶量很大，AMMSE的復雜度也較高。

在本文中我們結合AMMSE和符號迭代檢測的思想，提出了一種基于迭代的近似MMSE(I-AMMSE)方法。該方法主要是基于AMMSE的級數展開式，選擇合適的AMMSE的近似項數用于檢測，然后將解調器的信息反饋給檢測端迭代，迭代多次以獲得近似最優的性能。

該方法首先將接收信號經過合適項數的近似MMSE檢測器產生輸出，然后由K(用戶數)個解調器做后驗解調，然后根據解調后的結果和解調前的信息算出外信息反饋給近似MMSE端用于下一次迭代消除其他用戶的部分干擾，其中外信息以均值和方差的形式表現。然后重復上面的迭代步驟指導收斂。并且我們發現通過引入迭代，我們只需要取AMMSE的少數項就可以遠超過MMSE的性能，并達到接近最優的性能(無用戶干擾的性能)。

1 基本原理

1.1 信道模型

我們考慮如下上行信道：基站端有N個天線，服務于K個單天線用戶，則接收信號為式(1)。

(1)

r=Hx+z

(2)

其中假設矩陣H中的每個元素都是獨立同分布并具有0均值單位方差的復高斯隨機變量。

1.2 近似MMSE(AMMSE)檢測

MMSE可以由式(3)給出。

(3)

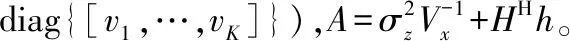
(4)

其中L是近似的項數。

2 迭代的近似MMSE(I-AMMSE)檢測

由上可知MMSE檢測需要求解矩陣逆運算，且AMMSE(4)中的L取值需較大才能獲得較好的檢測性能，這兩種方法復雜度都較高并且相比理想無用戶干擾性能相差較遠。通過引入信息反饋的思想，并基于AMMSE，我們提出了迭代的AMMSE(I-AMMSE)方法。

I-AMMSE的框圖，由修改的AMMSE(MAMMSE)和解調端DeMs組成。下面詳細介紹MAMMSE和DeMs兩部分，如圖1所示。

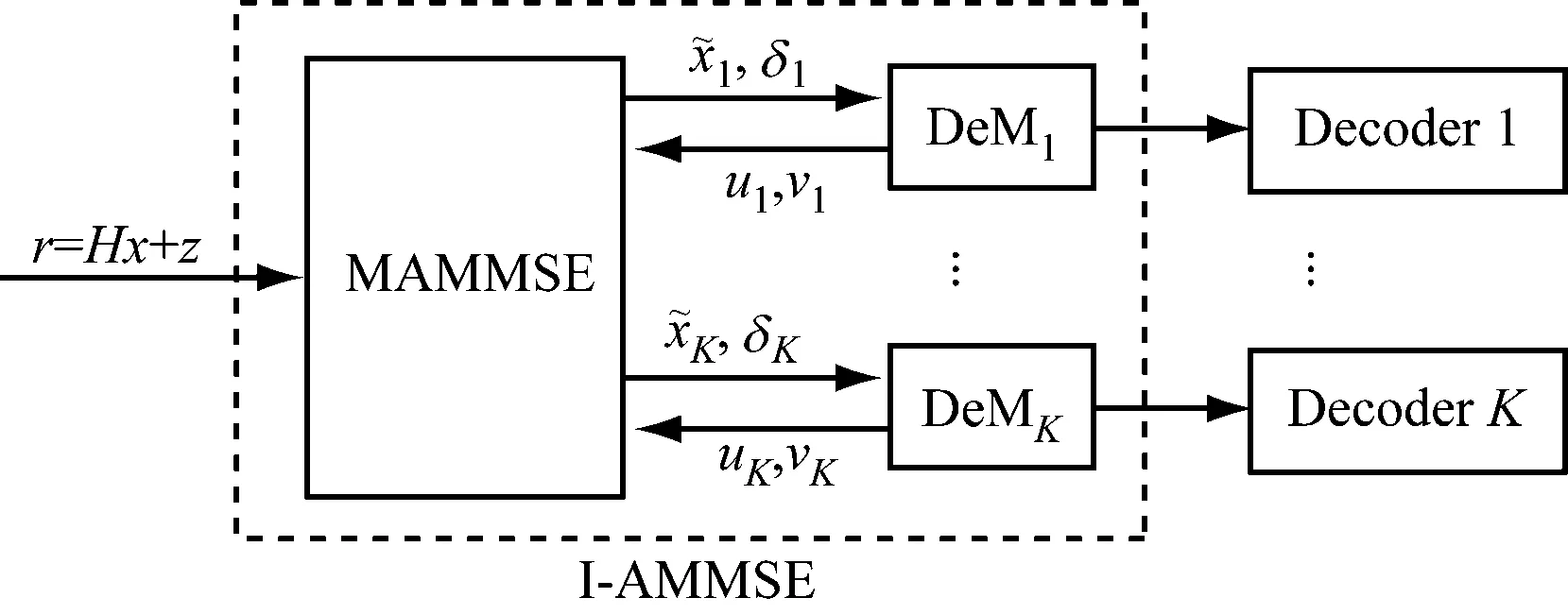
圖1 迭代AMMSE(I-AMMSE)接收機

框圖第一部分，MAMMSE基于接受的信號r和來自DeMs均值和方差信息的反饋，從而對x進行估計。用uk,vk表示xk的均值和方差，它們是DeM的反饋信息，注意在第一次迭代中因為沒有反饋信息，所以初始化uk=0,vk=1。為了估計xk，我們從(2)中減去其他用戶的干擾，則剩下的信號為式(5)。

(5)

(6)

則xk的估計為式(7)。

(7)

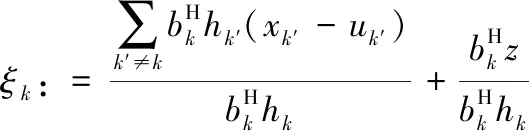
(8)

(9)

(10)

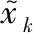
(11a)

(11b)

通過重復迭代的執行上面兩步，可以得到我們提出的I-AMMSE方法。算法的迭代過程如下，迭代次數Q可以根據性能和復雜度約束進行選擇。

算法： 迭代的AMMSE方法(I-AMMSE)

1: 初始化:迭代數Q，AMMSE近似項數L，所有用戶uk=0,vk=1；

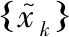
4: 循環: 重復步驟2和步驟3共Q次。

4 仿真結果

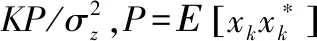
MF，MMSE，以及I-AMMSE算法在L=0和1的兩種情況下的性能比較曲線，如圖2所示。

圖2 16QAM下不同方法的性能

另外單用戶的線是最優的性能標準。由圖2我們可以看出，在L=0的情況下，I-AMMSE的性能在高信噪比時已經超過了MMSE的性能，并已達到近似最優的性能，但是在低信噪比時性能低于MMSE，這是因為低信噪比高階調制時，干擾和噪聲本身就較大，所以L=0項的AMMSE精度較差，多次迭代不會有所改善。但是在L=1時(也就是近似取兩項)，在低信噪比時，I-AMMSE的性能也有了很大改善，這相當于我們通過犧牲了部分可接受的復雜度獲得更好的性能，L值的選擇也即是復雜度和性能之間的權衡，可根據具體的應用場景而選擇合適的L值。

5 總結

針對大規模MIMO我們提出了一種的I-AMMSE檢測方法，該方法有效的利用迭代信息，以低復雜度達到近似無干擾的性能，并且其性能明顯超出MMSE方法。另外我們研究并仿真了通過選擇合適的AMMSE近似項數，可以獲得該檢測方法復雜度和性能之間的權衡，從而應用于不同需要的場景。