基于LSTM-RNN的質子交換膜燃料電池故障檢測方法

文/王森 雷衛軍 劉健 張伯林

1 引言

燃料電池是一種將燃料中的化學能轉化為電能的電化學設備。只要不斷的有氫氣和氧氣供應，燃料電池就可以源源不斷地輸出電能，并且反應產物中只有純凈的水，而不含其它污染物，是真正意義上的清潔能源。根據電解質和燃料的不同可以將燃料電池分為很多種，其中，質子交換膜燃料電池（PEMFC）是非常有前景的燃料電池之一，尤其適用于移動應用場景。有效的故障診斷策略可以幫助PEMFC電堆在相對最佳和有效的條件下運行，減緩燃料電池性能的下降，增加使用的可靠性和耐久性。因此，精準的故障檢測方法具有非常重要的實際意義。

目前，對于PEMFC故障檢測的方法主要包括兩大類：基于推理的方法和基于分類的方法。基于推理的方法主要通過已知或部分已知故障和現象之間的因果關系，運用邏輯推理進行故障排查，如故障樹、模糊關系和專家系統等。這類故障檢測方法的可釋性強，但是模型的準確度與先驗知識的正確性息息相關。同時，PEMFC電堆內部結構越復雜，模型的構建難度就越大，且模型的準確度也會隨之降低很多。

基于對數據進行分類的分類算法是近幾年來比較熱門的分類方法，以統計學為基礎，通過分析各種PEMFC相關的歷史數據或特征參數，對PEMFC電堆故障進行分類預測。這類方法不再依賴于先驗知識，而是根據實際采集的數據進行建模，屬于一種數據驅動的故障檢測方式。同時，這類故障檢測方法建模與電堆內部結構復雜程度無關，簡單快捷且成本低，因此，受到許多研究者的關注。常見的一些預測模型包括模糊聚類、支持向量機和神經網絡等。其中模糊聚類、支持向量機等傳統機器學習方法的一般建模流程為數據預處理、特征提取和選擇、模型訓練和驗證。其中特征提取和選擇是獲得高準確度模型非常關鍵的一步，提取和選擇的特征能否表征各類故障將直接影響分類超平面構建的正確性，通常特征提取和選擇過程相對復雜且需要一定的領域知識，難度比較大。相比傳統機器學習方法，神經網絡是一種仿生物神經網絡結構和功能的模型，可以自動學習到故障分類相關的特征，建立相應的預測模型，準確度得到一定的改善。因此，神經網絡在復雜的非線性系統的故障診斷領域得到了廣泛應用。

近年來，深度學習技術得到迅速地發展，驚人的非線性擬合能力和出色的抽象挖掘能力使得這項技術的應用領域不斷拓展。其中，循環神經網絡（RNN）將時序的概念引入到網絡結構設計中，隱藏層之間的互連結構反映出時間序列之間的相互影響關系，但是RNN存在著梯度消失、梯度爆炸和長期記憶能力不足等問題 。長短期記憶（LSTM）模型是RNN的一種變體，它通過在網絡中加入細胞結構（cell）彌補RNN的不足，從而對時序數據具有更強地適用性。LSTM模型已經被成功地應用到許多不同領域的時序數據處理當中。其中包括自然語言處理相關的語音識別、機器翻譯、情感分析等，醫學相關的時序 fMRI 數據分類、蛋白質二級結構序列預測等，媒體相關的視頻流數據分析，金融相關的股票指數預測，環境相關的空氣污染物預測等等。而在工業領域也有少量相關研究證明了LSTM的適用性，文獻[12]將LSTM模型應用于故障時間序列預測，并在民航飛機故障數據上實驗證明了LSTM預測模型的優越性能。文獻[21]將LSTM模型應用于鐵水硅含量預測，發現LSTM模型預測誤差穩定，比傳統的統計學及神經網絡方法具有更好的預測精度。

相比其他分類器，LSTM主要具有以下三點優勢：

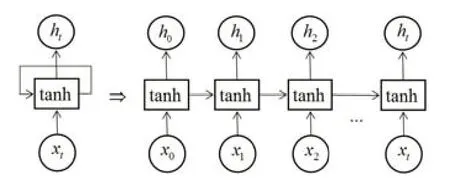
圖1：RNN網絡結構圖

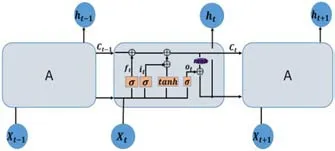
圖2：LSTM網絡結構圖

圖3：質子交換膜燃料電池故障檢測整體流程圖

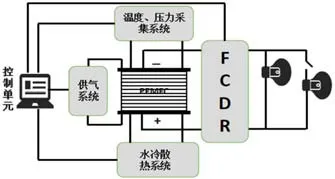
圖4：燃料電池系統結構圖

（1）相比傳統推理的方法，LSTM能夠更加準確且自動地從數據中提取特征，模型構建簡單高效、高準確度。同時，LSTM學習的是數據集的概率分布，所提取的特征比經驗更符合數據本身的概率分布。

（2）相比傳統機器學習方法，LSTM是一種深度學習的方法，可以自動學習到數據更深層次、更具體的特征，因而具有更好的非線性擬合能力和分類能力。

（3）相比于其它深度學習方法，屬于循環神經網絡的LSTM具有長久的時間記憶性，隱藏層的結構設計體現了時間序列之間的相互影響關系，具有更好的時序數據處理能力。

利用LSTM-RNN在分析時序數據方面的天然優勢，本文提出將該方法應用于質子交換膜燃料電池故障檢測，并進一步地運用貝葉斯優化方法選取最佳LSTM模型參數，以獲得簡單快捷且具有更高準確度的故障檢測方法。本文采集實際PEMFC電堆系統輸出的電壓、電流、母線電壓和母線電流四類數據展開實驗，無需嵌入其它復雜昂貴的傳感器監測，降低了故障檢測的成本。同時，本文將LSTM模型與RNN、SVM及神經網絡這三種常見的數據驅動模型進行實驗對比。實驗結果證明，LSTM 模型應用于質子交換膜燃料電池故障檢測的準確度得到提升。

2 基于LSTM-RNN的質子交換膜燃料電池故障檢測方法

本文將在這節內容中描述LSTM-RNN 神經網絡模型的結構、LSTM-RNN應用于質子交換膜燃料電池故障檢測的方法和模型參數的調優。

2.1 LSTM-RNN神經網絡模型

RNN最關鍵的網絡結構設計（如圖1所示）在于隱藏層的信息不僅傳遞到輸出層，還傳遞到下一時刻的隱藏層，從而允許信息的持久化。在訓練網絡時，每次誤差的反向傳遞不僅依賴于當前的網絡狀態，還依賴于之前的網絡狀態。這種互相影響的鏈式結構特征正好反映出時間序列之間的相互影響關系，進而表現出對時間序列很好的適用性。

但是由于梯度消失的問題，RNN未能真正表現出長久的時間記憶性，也就是在時間間隔增大時，RNN會失去學習久遠信息的能力。因此，有了LSTM模型的出現。

LSTM將簡單的RNN細胞替換成具有存儲功能的LSTM細胞，具體結構如圖2所示，由輸入門it，忘記門ft、輸出門ot和細胞狀態ct四部分組成。細胞狀態貫穿在整個鏈上，就像傳送帶一樣傳遞著信息流。三種門結構則選擇性地讓信息通過，對網絡中的信息流進行控制。其中，輸入門決定讓多少新信息加入到細胞狀態中；忘記門決定從細胞狀態中丟棄什么信息；輸出門基于細胞狀態決定最終輸出什么信息。各個部分的函數表達式如下：

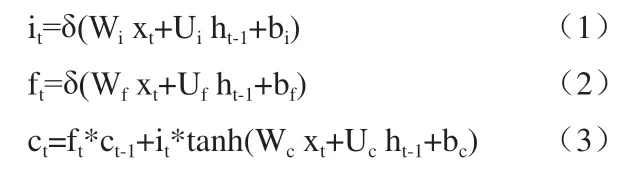
其中，it、ft、ot分別為輸入門、忘記門和輸出門；W為權值矩陣；U為隱藏層狀態權值矩陣；b為偏置項；ct為t時刻的細胞狀態；ht為t時刻的隱藏層狀態；δ是激活函sigmoid。

2.2 基于LSTM-RNN的質子交換膜燃料電池故障檢測方法

本文基于LSTM-RNN在分析時序數據方面的優勢，提出數據驅動的質子交換膜燃料電池故障檢測方法，以期獲得具有更高準確度的分類器，算法的整體流程如圖3所示。

傳感器采集的數據是一種持續的動態數據，本文按選定時間窗口長度L將所采集的數據分割成樣本序列。在t+1時刻，將傳感器采集到的數據進行歸一化處理，消除不同維度之間的量綱影響。然后將歸一化后的數據與t時刻LSTM的輸出一起輸入到LSTM，重復此操作直到長度為L的數據都輸入到模型中。最后通過輸出層得到最終的分類結果，輸出層為softmax層，輸出樣本屬于各個類別的概率。

2.2.1 數據集介紹

本文通過采集質子交換膜燃料電池電堆的輸出電壓、電流、母線電壓和母線電流四類數據。為了獲得質子交換膜燃料電池不同運行狀態的數據，本文通過改變操作條件手動引發電堆故障，例如，增加負載引發過載故障，設置電堆不同的工作溫度制造不同的溫度異常，改變電堆的工作壓力，制造不同的壓力異常。最終，根據電堆的不同運行狀態，將采集的數據分為正常、溫度異常、壓力異常、過載等，圖4為燃料電池電堆系統結構，圖5為燃料電池測試系統實物。

定義數據集格式為：[data,label]

其中，data為某種電堆運行狀態的采集數據；label為人工標注的data所屬狀態類別。

定義data的格式為：[time_step,sensor]

其中，time_step為觀測時間窗口內電堆運行狀態的采樣點數，維度為L；sensor為采集信息的種類，本系統由4種參數構成，維度為4。

2.2.2 網絡訓練

網絡訓練指的是通過學習訓練集中的數據分布獲取構建網絡所需的所有參數的過程。首先，將訓練集數據按式（6）進行最大最小歸一化處理，其中xt為t時刻傳感器所采樣的特征向量，min(x)為訓練集數據各維度最小值向量，max(x)為訓練集數據各維度最大值向量。

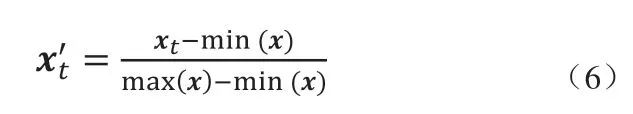
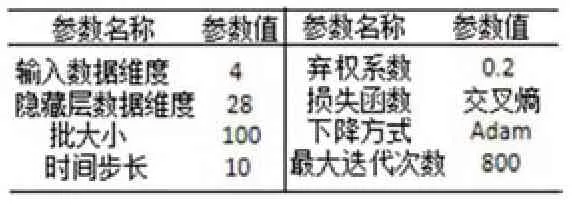
表1：LSTM參數設置表

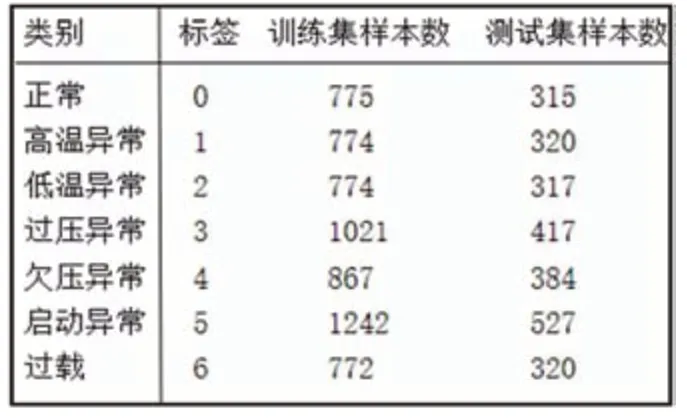
表2：數據集樣本類別分布情況表

表3：SVM參數設置表

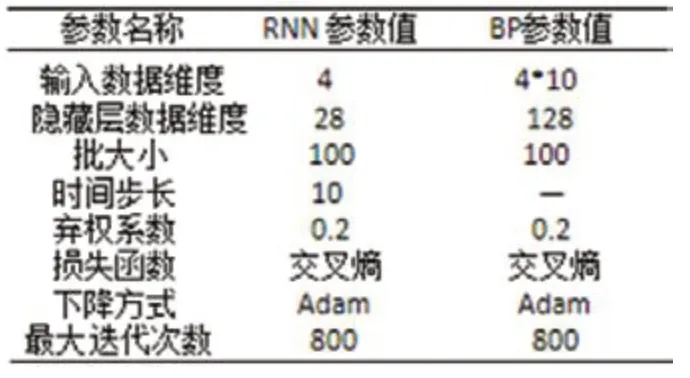
表4：RNN和BP神經網絡的參數設置表

圖5：燃料電池測試系統實物

為了適應LSTM隱藏層輸入的特點，應用數據分割的方法對訓練集數據進行處理，按時間窗口長度L將數據分割成data形式的樣本序列，取時間窗口最后一個時刻的電堆運行狀態為data對應的label。

然后逐步將一組樣本序列對應時刻的特征向量和上一時刻LSTM模型的輸出同時輸入到LSTM。在一組樣本序列輸入完畢后，由最終時刻的隱藏層輸出經過權值矩陣計算得到網絡輸出y。再經過softmax層將y映射成概率分布y'，即樣本序列屬于不同類別的概率。假設原始網絡輸出y=[y1, y2, …, ym]，m為樣本序列類別數，那么經過softmax處理后輸出y'=[y1', y2', …, ym']，計算公式如下：

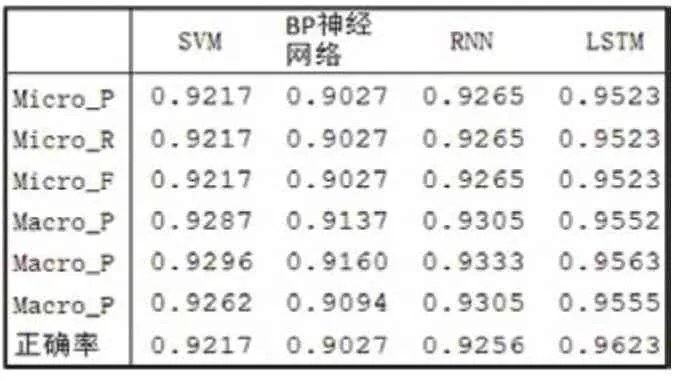
表5：不同算法的微平均、宏平均和正確率

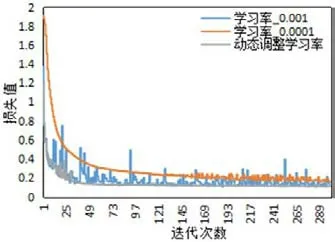
圖6：不同學習率的訓練損失

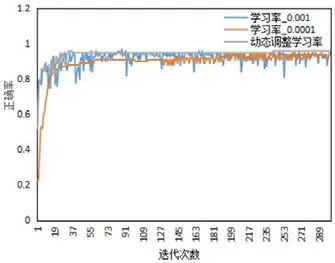
圖7：不同學習率的訓練正確率

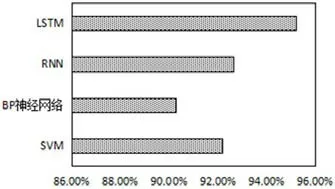
圖8：不同算法的模型正確率

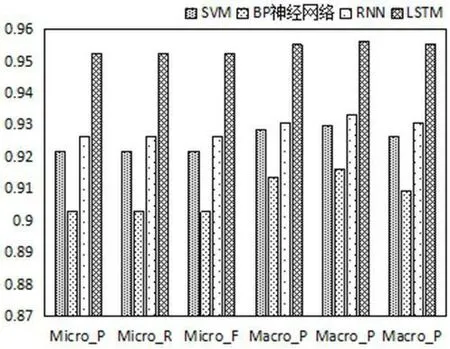
圖9：不同算法的宏平均和微平均

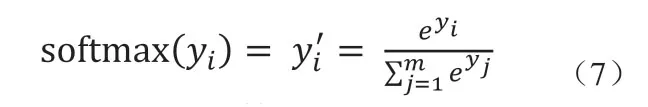
由于故障檢測屬于多分類問題，所以采用分類交叉熵函數（categorical crossentropy）作為誤差計算公式，表達式如下：

給定網絡隨機初始化種子seed、學習率learning_rate、隱藏層特征維度hidden_size、整體樣本迭代次數epoch和每次迭代批大小batch_size，以最小化損失函數為目標，計算誤差函數對權值矩陣的梯度，應用Adam優化算法不斷迭代更新權值矩陣，進而得到最終的網絡模型。

2.3 模型參數調優

超參數的設置是否合理極大地影響了模型的最終效果，包括對訓練集數據概率分布的擬合程度和對未知數據預測的泛化能力。超參數調優可以看作是以超參數為自變量的性能函數f(x)最優化問題。

其中，x為某一超參數組合；A為超參數組合取值空間。

對于超參數調優而言，目標函數f(x)是未知的且為非凸函數，因此，它又被認為是一個黑盒優化問題，即優化的目標函數通常不滿足凸優化條件，無法通過求導或凸優化方法求得最優解。目前，在眾多機器學習超參數優化方法中應用較為廣泛的分別是網格搜索、隨機搜索和貝葉斯優化。網格搜索的核心是通過遍歷搜索范圍內所有的超參數組合確定最優值。這樣的搜索方案雖然簡單，但隨著超參數個數的增加，超參數的組合近似爆炸性增長，十分消耗計算資源和時間，所以不適用于超參數較多的情況。隨機搜索認為在樣本集合足夠大的條件下，隨機采樣也可以找到目標函數的全局最優解或最優解的近似。因此，隨機搜索不再遍歷所有超參數組合，而是以隨機選取的方式選擇超參數組合，并從選擇的組合中返回最優結果。由于隨機因素的存在，隨機搜索的結果不太穩定，可能出現效果特別好，也可能出現效果特別差。貝葉斯優化算法的基本思想是基于數據使用貝葉斯定理估計目標函數的后驗分布，然后再根據分布選擇下一個采樣的超參數組合。相比于前兩個方法搜索的盲目性，貝葉斯優化充分利用已知點的信息學習目標函數后驗分布，再基于超參數每個取值點的均值和方差，有目的的搜索下一個采樣點。如此不僅大大減少了采樣次數和尋優時間，而且結果更易接近全局最優。

在LSTM模型構建時涉及眾多的超參數，因此，本文采用貝葉斯優化算法對模型的多個關鍵超參數進行調整：以參數為自變量，最小化負的測試集正確率為目標函數，即最大化測試集正確率，選擇最佳結果作為參數設置，具體如表1所示。

學習率也是LSTM的關鍵超參數之一，它的設置極大地影響了網絡的收斂效果。如果學習率太小，網絡的收斂速度就非常慢；反之，如果學習率太大，網絡容易在局部最優點附近來回跳動，導致不收斂。在網絡訓練初期，損失函數下降得快，應該設置大的學習率，而隨著網絡訓練次數增加，損失函數下降的速度逐漸減緩，則應該調整成小的學習率。因此，本文初始設置學習率為0.001，隨著訓練迭代次數的增加，逐步降低學習率。

3 實驗與結果分析

本節將使用實驗采集到的數據驗證質子交換膜燃料電池電堆故障檢測網絡的性能，并把SVM、RNN和BP神經網絡設為對照組，通過對比實驗證明LSTM網絡應用于電堆故障檢測的優勢。

3.1 數據集準備和評估指標

3.1.1 數據集準備

本文采集了約9萬個數據，每個數據都包含電堆的電壓、電流、母線電壓和母線電流4個維度的值。根據電堆的運行狀態對這些數據進行人工標注，包括正常、高溫異常、低溫異常、過壓異常、欠壓異常、過載和啟動異常，共7種標簽。綜合考慮故障檢測的及時性、穩定性和時間消耗，本文將時間窗口長度L設置成10，并按2.2.1節數據集格式存儲。數據集以7:3的比例隨機分成訓練集和測試集，用訓練集訓練網絡模型，測試集測試訓練好的模型性能，各個類別樣本分布情況如表2所示。

3.1.2 評估指標

常見的二分類器評估指標有準確率（Precision，P）、召回率（Recall，R）以及這兩個指標的調和函數F值（F-measure），計算公式為（10）～（12）。

其中，TP為正確預測為正樣本的個數，TN為正確預測為負樣本的個數，FP為錯誤預測為正樣本的個數，FN為錯誤預測為負樣本的個數。

類似地，在多分類問題中則用這三個指標的平均值做為分類器的評估指標。根據平均值的計算方式不同，可以分為宏平均（Macroaverage）和微平均（Micro-averaging）。宏平均先計算每一個類別i對應的準確率Pi，召回率Ri和Fi值，然后求所有指標的算術平均值Macro_P、Macro_R和Macro_F，計算公式為（13）～（15）；微平均則先計算所有類別總的Micro_P和Micro_R，然后再計算Micro_F，計算公式為（16）～（18）。 電堆故障檢測屬于多分類問題，所以本文使用宏平均和微平均做為評估指標。

其中m為類別數，Pi、Ri和Fi的計算公式如（10）～（12）。

此外，本文還計算了模型的正確率（Accuracy），作為模型整體準確度的一個評價標準，計算公式為（19）。

3.2 對照實驗設置

SVM是故障檢測領域常見的機器學習算法之一，以最大化支持向量到分類平面的距離為核心。為了解決數據非線性可分問題，SVM一方面引入懲罰因子和松弛項，降低部分支持向量到分類平面距離要求；另一方面引入核函數，隱性地將低維非線性可分特征映射到更高維線性可分特征空間中。RNN和BP神經網絡均屬于深度學習領域的方法，其中RNN和LSTM一樣也是循環神經網絡，而BP神經網絡是目前使用最廣泛的神經網絡之一，能夠學習和存儲大量的輸入輸出映射關系，具有很好的非線性擬合能力。學習過程主要是通過反向傳播來不斷調整網絡的權值和閾值，使網絡的誤差平方和最小。

為了對比各方法在空間燃料電池故障分類方面的性能，SVM的參數設置也采用貝葉斯優化方法進行調整，將RNN和BP神經網絡的關鍵參數設置與LSTM一樣。本文SVM參數設置如表3所示，RNN和BP神經網絡參數設置如表4所示，其中BP神經網絡使用sigmoid激活函數。

3.3 結果分析

本文測試了不同學習率對網絡收斂效果的影響，包括減少損失函數和提高模型正確率兩個方面。測試結果如圖6和圖7所示，從中可以看出學習率設置成過大的固定值0.001時，網絡在局部最優點來回跳動，損失函數和模型正確率都出現明顯的震蕩現象，網絡不收斂。相反，學習率設置成固定值0.0001時，網絡收斂的速度明顯變慢且收斂效果不佳，損失值和正確率都不如動態調整學習率的好。顯然，動態調整學習率的效果最佳，初始學習率大，損失函數下降得快，正確率提升快，迭代一定次數后，調整成小學習率，網絡收斂更穩定，且收斂結果更優。

為了證明LSTM模型對空間燃料電池故障序列的分類性能，本文依據3.1的評估指標和3.2的對照實驗設置，進行10次重復實驗，取測試集的平均值作為最終結果，記錄在表5中，對比結果如圖8和圖9所示。

從表5、圖8和圖9可以看出，LSTM的模型性能最佳，正確率達95%以上，比正確率第二的RNN高出近3%，宏平均和微平均也都在0.95以上，高于其它對比算法。同時，可以看出RNN和SVM模型分類效果相近，BP神經網絡的分類效果稍差些。結果證明，LSTM模型能夠充分挖掘空間燃料電池故障序列的特性，具有很強的時間序列適用性。

為了進一步分析LSTM模型對不同故障的分類效果，本文測試了LSTM模型的混淆矩陣，橫軸為樣本的真實標簽，縱軸對應預測標簽，結果如表6所示。

從表6可以看出，LSTM模型對故障1和6的分類正確率達100%，故障2的達99%以上，故障5的97%以上。相比于其它類別，標簽值為3和4的分類正確率稍差，說明模型對過壓異常和欠壓異常數據特征挖掘不夠，區分能力稍弱。

進一步地，本文測試了同為深度學習方法的LSTM、RNN和BP神經網絡的模型訓練情況，結果如圖10和圖11所示。

從圖10和圖11可以看出，針對訓練集LSTM和RNN的訓練效果相近，BP神經網絡的效果較差。而測試集中，LSTM模型的正確率高出RNN近3%，宏平均和微平均也明顯高于RNN。由此，證明了本文的LSTM模型泛化能力比RNN強，對數據特征表征更準確，更真實地擬合了數據的分布情況。

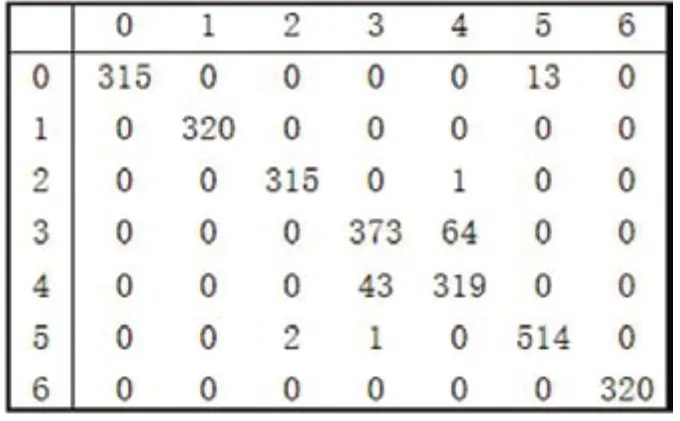
表6：LSTM模型混淆矩陣

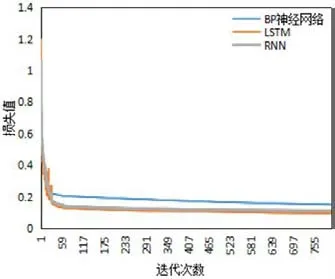
圖10：不同算法的訓練損失

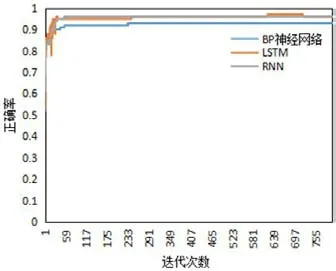
圖11：不同算法的訓練正確率

4 結語

本文針對空間燃料電池故障序列的時間特性，利用LSTM模型對故障序列進行分類檢測。實驗證明，LSTM模型具有很好的時間記憶性，能夠充分挖掘故障序列時間特性。對比LSTM和其它算法的分類結果，可以看出LSTM的分類正確率、宏平均和微平均都是最優的，并且LSTM比RNN具有更好的泛化能力，對數據集的分布擬合得更準確。由此，說明了本文所提方法的可行性和優越性。

另外，本文還證明了不同學習率對LSTM模型訓練效果的影響，動態調整學習率不僅可以加快模型的收斂速度，提高模型的穩定性，而且可以使模型收斂到更優的結果。同時，本文還具體分析了LSTM模型對不同故障分類的效果，發現模型對過壓故障和欠壓故障的分類效果稍差，需要在后續工作中改進。