基于協同過濾的多維度電影推薦方法研究

張家鑫，劉志勇，2，張琳，張倩，莎仁

（1.東北師范大學 信息科學與技術學院，長春 130117；2.東北師范大學 教育部數字化學習支撐技術工程研究中心，長春 130117；3.吉林大學 軟件學院，長春 130012）

隨著互聯網基礎設施建設的不斷優化升級，移動端智能設備的不斷普及，用戶瀏覽互聯網的體驗有了巨大的提升，人們對互聯網的需求日益增多，互聯網已經完全融入了人們的生活，成為了與之密不可分的重要組成部分［1］。用戶如何從大量數據中快速便捷選擇出有效信息的需求日益增加，搜索引擎的出現初步解決了這一問題。但是，隨著信息的爆發式增長，用戶的需求往往較為模糊［2］，所以如何通過用戶的個人信息、瀏覽記錄等為用戶進行信息推送，減少因用戶的模糊需求影響信息獲取的效率，推薦系統的出現較好的解決了這一問題［3］。

推薦系統在1997年由Resnick和Varian提出，其中協同過濾推薦方法出現較早并且應用廣泛，是推薦系統中最重要的推薦方法之一［4］。推薦系統廣泛應用電子商務、電影和視頻、音樂、社交網絡、個性化閱讀、個性化郵件、基于位置的服等領域，其中較為典型的包括Amazon、Netflix等。據Amazon統計，推薦系統的應用使平臺的銷量增加35%。Netflix公司曾在2006年舉辦Netflix Prize大賽，該大賽為了獎勵可以提升Netflix平臺的影片推薦效率［5］。推薦系統發展至今，由于用戶的個人狀態以及所處環境的差異，使得進行推薦的情景也不斷增加，在視頻和音樂推薦領域顯得較為突出。以電影推薦為例，傳統的協同過濾推薦方法在進行推薦時，只考慮了用戶和項目的二維關系，忽略了包括環境因素、影片信息、觀影感受等多維度影響因素，這會導致與用戶的實際傾向存在一定的偏差［6］，針對這種情況，本文提出了基于協同過濾的多維度電影推薦方法，主要改進如下：以電影推薦為例，首先通過回歸模型確定有效的多維度因素以及維度內的屬性，接下來通過進一步確定各維度屬性對于預測評分的影響程度和權重，獲得多維度預測模型，最后將多維度評分模型與傳統協同過濾推薦模型結合，通過實驗的方法，確定結合后的模型，驗證模型推薦準確率。

1 相關研究

為提升協同過濾推薦方法的推薦效率，許多研究者在傳統協同過濾推薦方法的基礎上進行了改進，例如：牛常勇等［7］通過SVD方法緩解數據集的稀疏與冷啟動問題。王茜等［8］通過引入時間遺忘函數、拈度函數、用戶特征向量，對協同過濾算法尋找用戶的最近部居集合過程進行了改進，提高推薦的準確度。王曉軍［9］構建基于分布式的混合協同過濾方法，緩解稀疏矩陣問題，改善推薦精度。邢哲等［10］提出了多維度自適應協同過濾推薦方法，該方法融合了基于項目、用戶、評論的協同過濾模型，實現精準預測。張世顯［11］等提出了引入時間維模型作為評分權重，解決了興趣遷移的問題。

本文提出的改進方法與上述方法不同，通過引入對推薦結果可能有影響的多維度因素，利用回歸分析的手段進行多維屬性因素選取并構建多維度評分模型，最終與基于用戶的協同過濾模型有機結合，構建基于協同過濾的多維度推薦模型。

1.1 協同過濾推薦方法

協同過濾推薦方法的主要思想是利用他人的歷史記錄或項目評分為目標用戶進行產品推薦或項目評分［12］。協同過濾推薦方法由以下三個步驟組成，包括構建用戶-項目評分矩陣、尋找相似目標、預測評分進行推薦。

其中尋找向目標的方法為計算用戶相似度計算，根據計算用戶-項目評分矩陣（表1所示）尋找當前與用戶Ui的最近鄰相似用戶。

表1 用戶-項目評分矩陣

用戶相似度的計算方式主要包括余弦相似度計算（Cosine-Based Similarity）、皮爾森相關系數（Pearson-Correlation Coefficient）、杰拉德系數（Jaccard），本文采用皮爾森相關系數。

設Iuv為用戶u和用戶v共同評分過的項目集合，則用戶u和用戶v的相似度度量方法如式1所示：

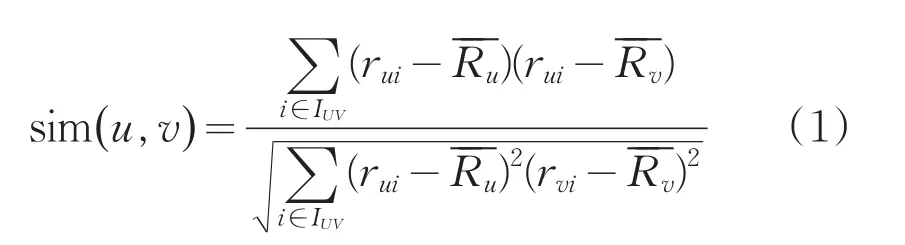
基于目標用戶u與其他用戶v的相似度，對其他用戶相似度進行排序，取前k個為當前用戶u的最近鄰集合KNN-u，根據該集合預測用戶u對項目i的評分，計算方式如式2所式：

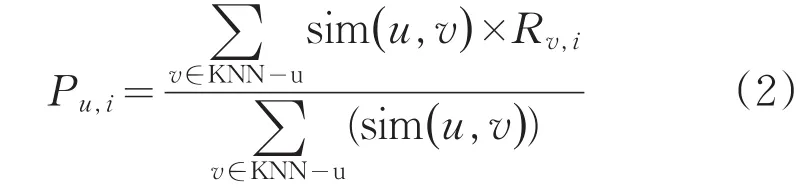
式中，Ru.i和Rv.i分別表示用戶u對項目i的評分和用戶v對項目i的評分，分別表示用戶u和用戶v的平均評分，KNN-u代表目標用戶u的最近鄰集合。

1.2 線性回歸

線性利用數理統計中的回歸分析來確定兩種或兩種以上變量之間相互依賴的關系，運用廣泛［13］。本文選取多元回歸模型進行維度確定，多元回歸模型的一般形式如3所式：

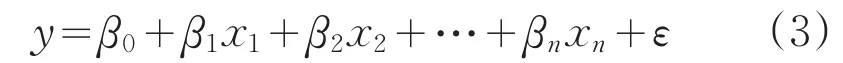
式中，ε為隨機誤差，E(ε)=0。β0,β1,β2,…,βn為回歸系數，若回歸系數為正數，則表示y隨著x的增大而增大，且x對y的影響程度與|β|成正比。

1.3 多維度推薦

傳統的推薦系統是基于用戶-項目二維度量空間，未考慮情感信息、環境信息等相關信息，忽略了隱式反饋信息對預測評分的重要性，然而用戶對項目的評分是由多個因素共同決定的，所以多維度推薦方法對推薦準確率能有一定的提高。

可以認為多維度推薦預測評分由用戶與多維因素共同決定，故定義用戶-多維度評分矩陣如式4所示：

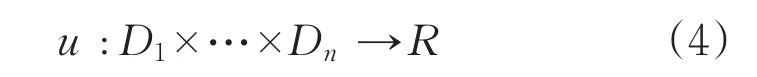
定義d為多維度內的因素屬性，dnm為維度Dn中的屬性m，(dn1,dn2…dnm)∈Dn。

2 多維因素分析與選取

本文進行的多維因素分析是以視頻推薦為背景，通過用戶觀看電影的多維信息因素進行數學模型的建立，最終確定哪些因素會影響用戶對電影的評分。其中，多維度影響因素周邊環境、觀影時的心情、觀影時的身體狀況等相關信息組成。

2.1 構建回歸模型

對數據中可能影響評分的多維屬性構建回歸模型，將選取線性回歸（Linear Regression）方式進行函數擬合，最終獲得對評分影響較大的屬性因素。線性回歸模型通過RapidMiner工具進行模型構建，步驟如下：

（1）數據預處理，在讀取數據后，利用Shuffle算子將樣本隨機打亂，并將原始數據分為兩份，訓練集用于建模，測試集用于模型評估。

（2）進行建模，將預測評分屬性設為標簽屬性，利用Linear Regression、Apply model算子進行模型構建，Performance算子進行模型評價。

（3）獲取線性回歸模型結果，利用評價指標對模型表現進行評估，抽取對預測結果影響較大的屬性。

2.2 多維評分模型構建

通過初步回歸分析，獲得了有效的多維影響因素，接下來對已抽取的影響因素進一步回歸分析，進而確定多維因素屬性的權重。

假設獲取有效的屬性因素k個，記錄各影響因素屬性相關系數為β1,β2,…,βn，定義各屬性因素權重為β1,β2,…,βn，因此定義各屬性維度評分模型如式5所示：

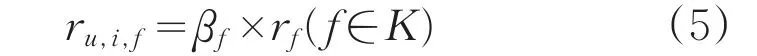
式中，K為屬性集合，rf表示屬性因素f的屬性值，βf為屬性f的權重，ru,i,f為用戶u對于項目i在屬性f在下的預測評分。

定義多維度評分模型如式6所示：

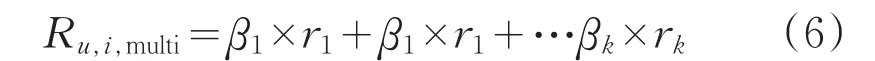
可化簡為式7：

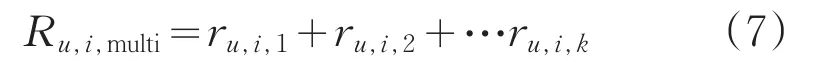
式中，Ru,i,multi為用戶u對于項目i的多維度預測評分。

3 多維度協同過濾評分模型提出

個性化推薦中最為關鍵的環節是通過推薦模型計算出用戶對未評分的項目進行評分預測。傳統的協同過濾方法在進行評分預測時，僅僅考慮了用戶和項目兩個維度。為了將多維度影響因素添加到評分預測中，本文在原有協同過濾推薦方法的基礎上提出了基于協同過濾的多維度推薦方法。

3.1 傳統協同過濾評分模型

本文選取基于用戶的協同過濾推薦方法進行實驗比較，具體步驟如下：

（1）數據輸入，獲取用戶評分矩陣M（u，i），根據矩陣計算用戶相似度，得到與用戶u相似的用戶集合U。

（2）對于?u∈U，找到與用戶u相似的最高的k個最近鄰v，最近鄰用戶集合為KNN（u，v，k）。

（3）選擇出KNN集合中的商品，除去用戶u已評分的商品，通過評分模型進行分數預測。

（4）數據輸出，獲取用戶u對商品i的預測評分，按照預測值降序進行TOP-N推薦。

3.2 多維度協同過濾評分模型

在傳統的協同過推薦中，只考慮了相似用戶對項目的評分從而計算目標用戶的預測評分，該方法存在著預測評分獲取單一、易受主觀因素影響等問題，因此提出多維度協同過評分模型，在傳統協同過濾方法的基礎上添加多維度信息，充分考慮主客觀因素，涵蓋顯式反饋信息與隱式反饋信息，使預測評分變得更加合理。舉個簡單的例子，假設用戶u對影片a、b、c均進行了評分，其中對影片a、b評分略高于影片c，考慮到用戶在觀看影片c時的環境因素不同于觀看影片a、b時，所以簡單的認為用戶u對影片a、b的喜好程度大于影片c的觀點是片面的，不同用戶的評分依據除了對影片本身的喜好程度之外也包含著用戶的觀影環境、觀影心情等種因素影響，為解決這一問題，故提出了基于協同過濾的多維度電影推薦方法，在已知用戶對影片評分的基礎上進一步考慮多維度因素對于用戶評分的重要程度。

通過將2.2中定義的多維度評分模型與基于用戶的協同過濾評分模型進行擬合，構建基于協同過濾的多維度評分模型，定義模型如式8所示：

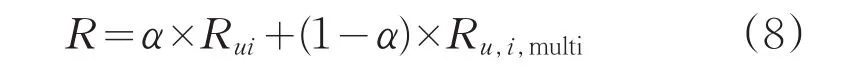
式中，R代表多維度協同過濾評分模型的預測評分，α為模型擬合系數，α∈(0,1)。

構建該評分模型的流程圖如圖1所示：

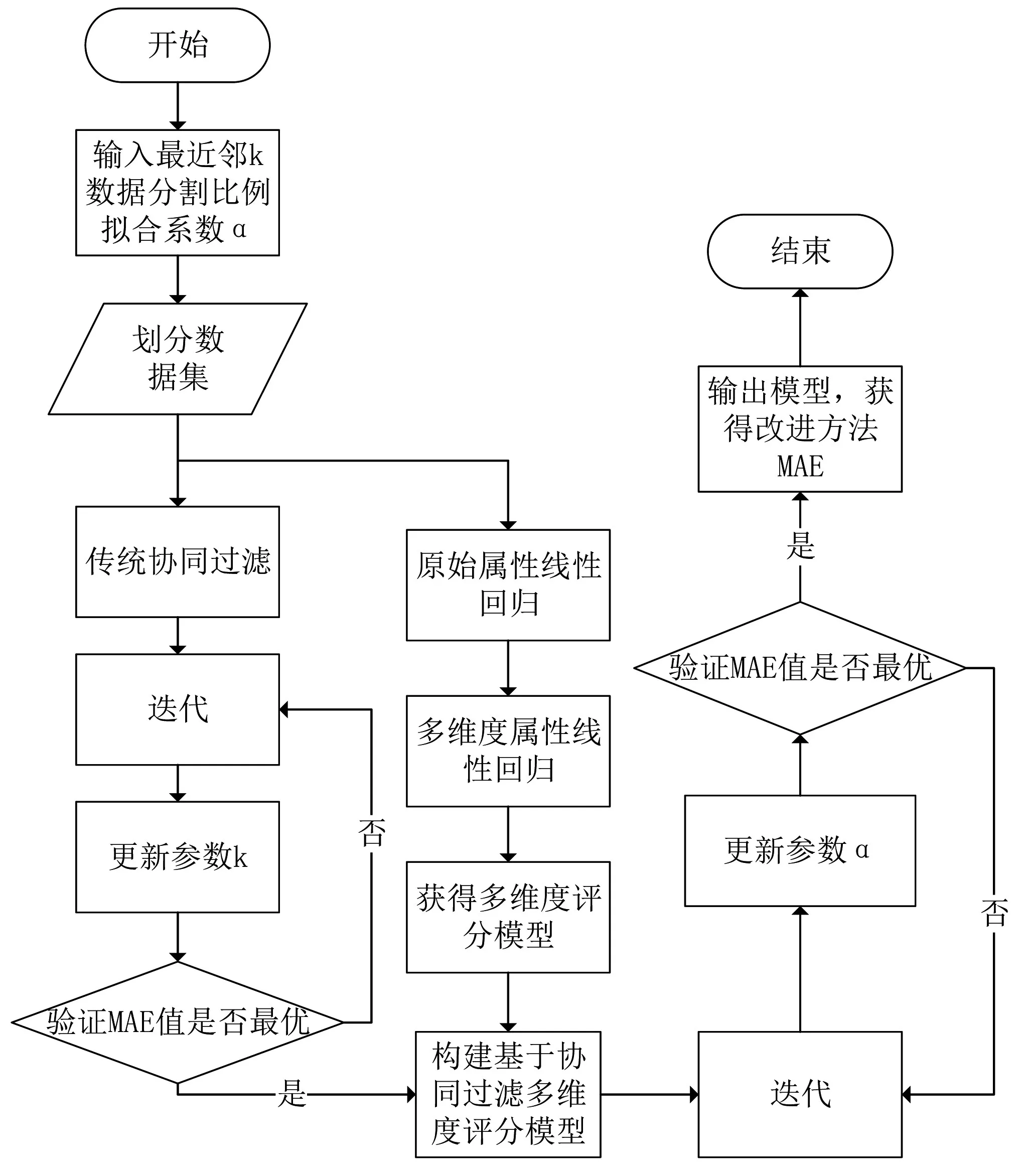
圖1 基于協同過濾的多維度推薦方法流程圖

4 實驗數據與結果分析

本節主要是將本文提出的基于協同過濾的多維度推薦方法與傳統的協同過濾推薦方法進行實驗對比分析，以驗證多維度推薦方法的有效性。分別通過數據集中的實驗集和測試集來計算出兩種推薦方法的推薦準確率，通過比較準確率驗證改進方法的適用性。

4.1 數據集及實驗環境

本文選取的數據集為LDOS-CoMoDa，其中包含了121個用戶對1232部電影的2296條評分記錄。LDOS-CoMoDa數據包含了用戶信息、影片信息、環境信息、評分信息等30個屬性因素，通過回歸分析后，最終選擇出對預測評分影響較大的7個有效屬性因素，并且根據有效屬性定義了5個不同維度。具體定義維度-屬性表如表2所示。

實驗環境為：Windows 7操作系統，8GB內存，Intel（R） Core（TM） i7-6700HQ CPU 2.60GHz，實驗程序使用Rapid Miner Studio 9.0開發。

4.2 評價標準

推薦系統評價是驗證推薦系統是否合格的重要環節之一，常用指標包括準確度與決策支持精度［14］，本文主要使用統計精度度量中的平均絕對誤差（Mean Absolute Error）來進行模型評價。

平均絕對誤差（MAE）的評價方式為計算預測評分與實際評分二者的絕對平均誤差，MAE越小，代表預測結果更趨近于真實值，即推薦結果較優。MAE評價公式如式9所示：

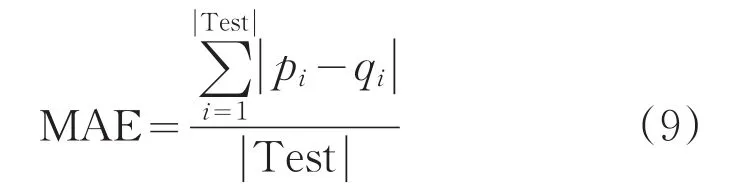
式中，| Test|為測試集合，pi表示用戶對集合中各項目的實際評分，qi表示預測得分。

4.3 實驗設計與結果

表2 多維度數據集維度-屬性表

為了使測試結果更加準確，在進行基于用戶的協同過濾方法與基于協同過濾的多維度推薦方法實驗時，將數據集隨機分為10份，輪流將其中9份作為訓練集，1份作為測試集進行實驗。

4.3.1 傳統協同過濾實驗

本文選取基于用戶的協同過濾方法進行實驗，實驗中設定近鄰數量k的取值范圍為［5，100］，采用區間漸進的方法，間隔為5，通過調整k值來觀察實驗結果。由圖1可以看出，傳統協同過濾推薦方法的MAE值在（0.92，0.99）范圍內波動，當k=50時，MAE取最小值，MAE=0.921，此時該方法推薦效率最高。

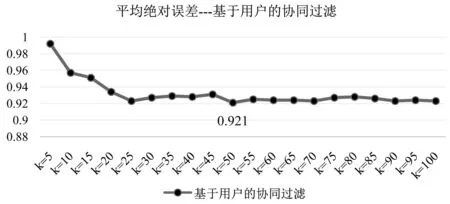
圖2 基于用戶的協同過濾方法MAE

4.3.2 多維度協同過濾推薦實驗

通過回歸分析，首先選擇出對預測評分影響較大的7個有效屬性因素及屬性權重（詳見表2），進一步基于已選擇的影響因素構建多維度評分模型，再通過式8，可構建基于協同過濾的多維度推薦模型。由于式8中的α未知，下面將通過實驗的方法選取較優的α值使改進方法的MAE取值降至最低。

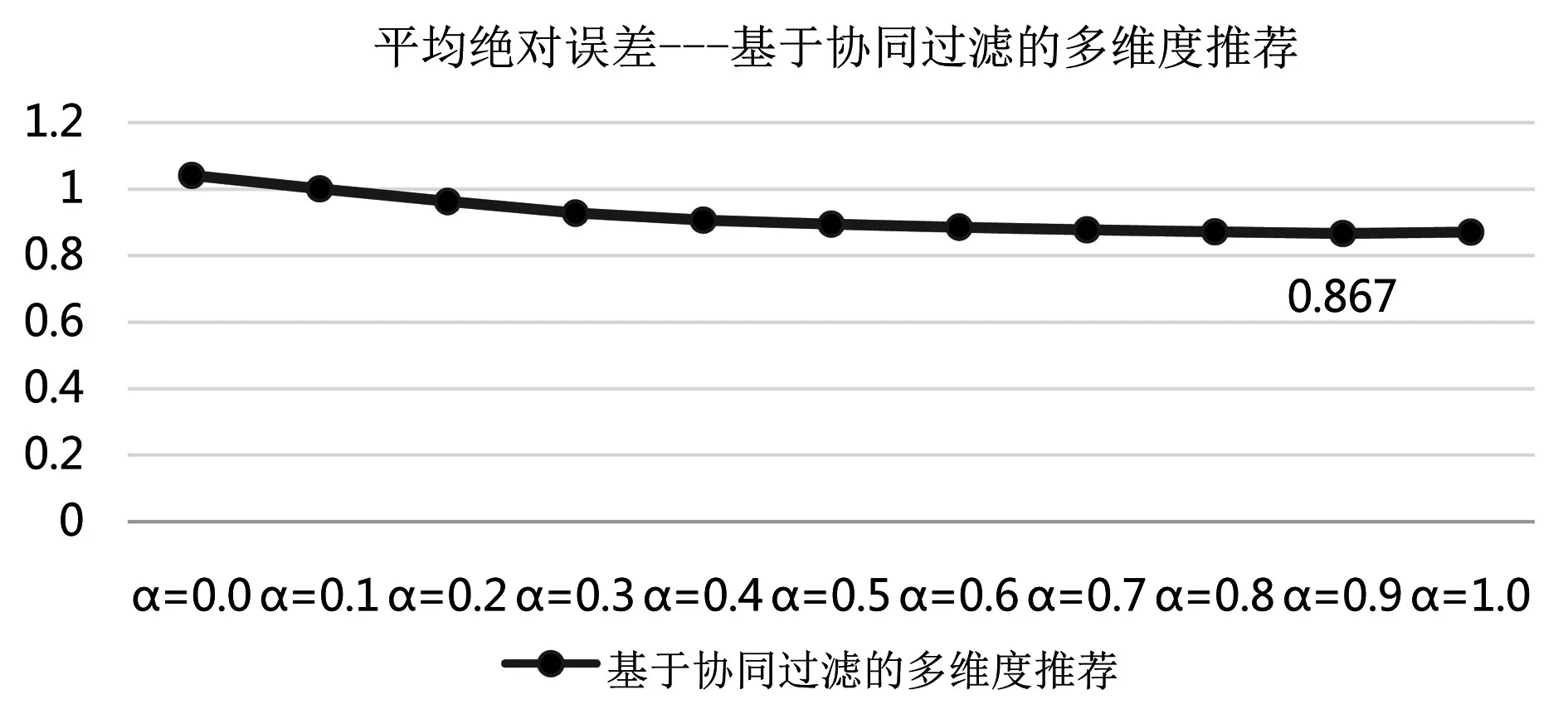
圖3 基于協同過濾的多維度推薦方法MAE

通過圖2所示，傳統協同過濾方法在k=50時，MAE取值降至最低，故默認改進方法中協同過濾算法的k值保持不變。

實驗中，設定改進的推薦方法中α取值范圍為［0，1］，采用區間漸進法，間隔為0.1，通過調整α取值，獲得不同的改進方法MAE取值，實驗結果如圖3所示。可以看出，基于協同過濾的多維度推薦方法的MAE取值范圍在（0.86，1.04）波動，當α取值為0.9時，MAE獲得最小值，此時MAE=0.867，推薦效果最優。

推薦模型可以定義為如式10所示：

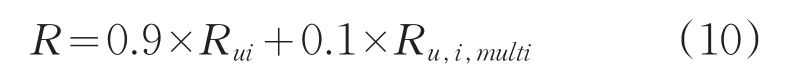
4.3.3 結果對比分析

通過上述實驗，獲得了傳統協同過濾推薦方法與基于協同過濾的多維度推薦方法的實驗結果，將實驗結果匯總到圖4中。選取實驗結果中的MAE最優值和MAE平均值進行兩種推薦方法的比較。在傳統協同過濾推薦方法中，當最近鄰k=50時，MAE值為0.921，此時該推薦效果最優。在基于協同過濾的多位推薦方法中，當擬合系數α=0.9時，MAE值為0.867，此時該推薦方法效果最優。

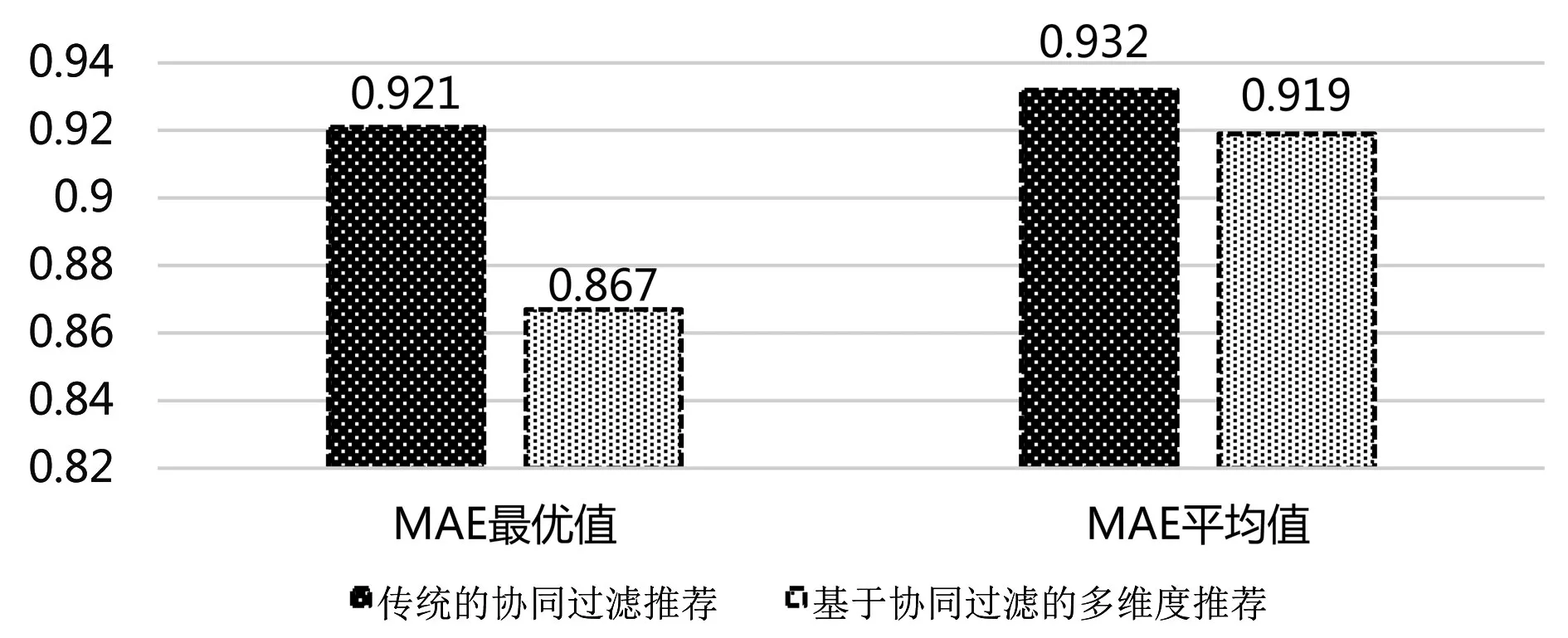
圖4 平均絕對誤差對比

在MAE均值方面，傳統的協同過濾推薦方法中，最近鄰k的取值范圍為［5，100］，在取不同k值情況下，該方法的MAE均值為0.932。基于協同過濾的多維推薦方法中，擬合系數α的取值范圍［0，1］，在取不同α值的情況下，該方法的MAE均值為0.919。

對比上述兩種推薦方法，基于協同過濾的多維度推薦方法相比傳統協同過濾推薦方法的推薦效果有一定的提升，其中最優MAE取值下降了約6%，MAE均值下降了約2%。

5 結論

本文在傳統協同過濾推薦方法的基礎上通過線性回歸確定了多維度影響因素及權重，并將多維度評分模型與傳統協同過濾推薦方法相結合，提出了基于協同過濾的多維度電影推薦模型，最后通過LDOS-CoMoDa數據集進行驗證。實驗結果表明，本文提出的基于協同過濾的多維度電影推薦方法優于傳統的協同過濾推薦，其中基于協同過濾的多維度電影推薦方法的最優MAE取值相比于傳統方法下降了6%，MAE均值下降了約2%，說明合理引入多維影響因素會對推薦效果有一定的提高，從而側面反應了影響用戶的預測評分是受多種因素影響的，單一維度的預測方式不足以應對復雜的推薦場景。但是，本文提出的基于協同過濾的多維度電影推薦方法也存在著不足之處，回歸分析采用的方法為線性回歸，在應對離散數據時擬合效果較差，其次是場景選擇是針對視頻的推薦，在面對其他應用場景進行推薦時有一定的局限性。下一步將對以上問題進行總結，在未來的研究中將重點改善回歸分析模型的選擇適用性以及應用場景的豐富性。