自由空間中集群式有源噪聲控制系統布放對穩定性的影響分析

玉昊昕，陳克安

(西北工業大學 航海學院 環境工程系，西安710072)

一般來說，集中式多通道有源噪聲控制系統在計算饋給次級源的控制信號時，需要使用所有次級通路傳遞函數的信息和所有誤差傳感器的信號[1]。集中式多通道有源降噪系統有利于提高降噪量和擴展降噪區域，目前已經廣泛運用在各種有源降噪工程中[2]。然而隨著次級源和誤差傳感器數量的增多，實現集中式系統所需要的計算量和成本隨之成指數級增長。在實際工程中，可以采用分散式控制策略來降低大規模有源噪聲系統的實現難度和成本，分散式系統將集中式系統拆分為多個獨立的單通道子系統，每個子系統只有一個次級源和誤差傳感器，各個子系統獨立運行，而不考慮各個子系統之間的聲耦合[3]。然而忽略子系統之間聲耦合作用將導致系統整體性能的下降并可能導致系統不穩定[4–5]。

集群式系統是一種新的系統實現策略，它介于集中式系統和分散式系統之間，如圖1所示。

圖1 集群式系統示意圖

集群式系統包含多個規模不一的子系統，各個子系統之間雖然互相獨立，但子系統本身是一個小規模的集中式系統。

類似的系統在振動或振聲控制中也稱為分布式（distributed）控制系統。在振聲控制的研究中發現某些代價函數下，分散式系統性能顯著差于集中式系統，而當使用模塊優化和局部代價函數時，分布式系統性能與集中系統一致[6]。而在平板結構的振動控制中，分散式控制雖然能達到與集中式控制相近的性能，但是并不能保證收斂[7]。

與分散式系統相比，集群式系統由于各個子系統更多地考慮了自身次級源和誤差傳感器之間的聲耦合，因此有更好的穩定性[6]；與集中式系統相比，由于子系統規模減小，又大大降低了系統實現難度和成本，是介于集中式和分散式系統之間的折衷形式。

由于常見的噪聲可以在頻域分解為各個頻率，因此本文通過建立集群式系統在單個頻率噪聲下的理論模型，并將控制迭代公式轉換為線性時不變系統傳遞函數[8]，分析系統布放對傳遞函數零極點的影響，得出使集群式系統在自由空間中保持穩定的系統布放原則。

1 理論分析

1.1 控制算法

考慮有I個子系統的集群式系統，每個子系統包含的次級源和誤差傳感器數均為N，使用多通道FxLMS 算法。顯然當I=1 時，集群式系統等效為集中式系統，當N=1 時等效為分散式系統。為了簡化分析，假設每個誤差傳感器處的初級噪聲均為由一個正弦信號經過初級通路模型產生的單頻信號。所有子系統均使用該正弦信號作為參考輸入，如式(1)所示，式中ω為信號的數字頻率，n采樣時間。

這樣，整個系統的次級源和誤差傳感器總數均為NI，從第j個次級源到第k個誤差傳感器的次級通路傳遞函數在頻率ω處的響應為

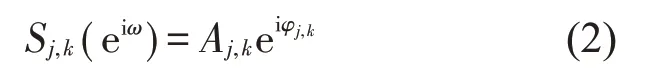
因此相應的濾波x信號為

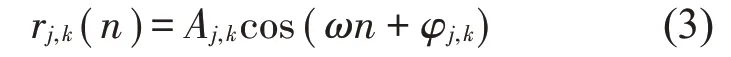
假設所有的子系統有相同的控制濾波器長度L與迭代系數μ，并在同一時刻開始控制，則誤差信號和控制器系數迭代公式分別為

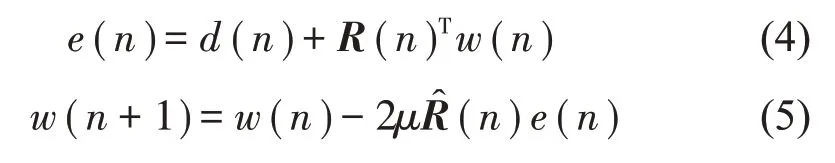
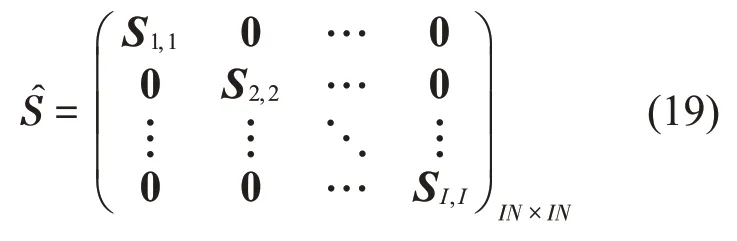
式中：e(n)為各個誤差傳感器接收到的誤差信號矢量，d(n)為各個誤差傳感器處的初級噪聲信號矢量，R(n)和為如式(6)和式(7)所示的濾波x 信號矩陣。由于子系統之間在物理上的互相影響是實際存在的，因此R(n)是所有元素均不為0的方塊矩陣；而子系統之間互相獨立，每個子系統只有自身的次級通路和誤差信號信息，在進行系數迭代時無法考慮其它子系統的影響，因此是對角方塊矩陣。

式(6)和式(7)中的Rp,q(n)表示第p 個子系統的傳感器到第q個子系統的次級源之間的次級通路脈沖響應，如式(8)所示。

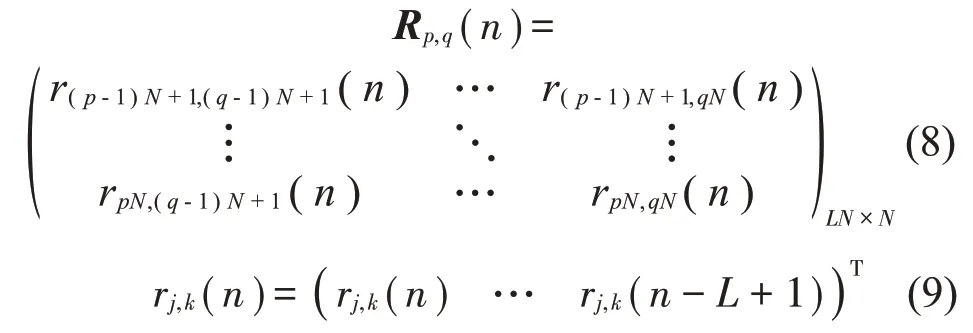
式中：w(n)為自適應濾波器控制系數矢量，如式(10)到式(12)所示。

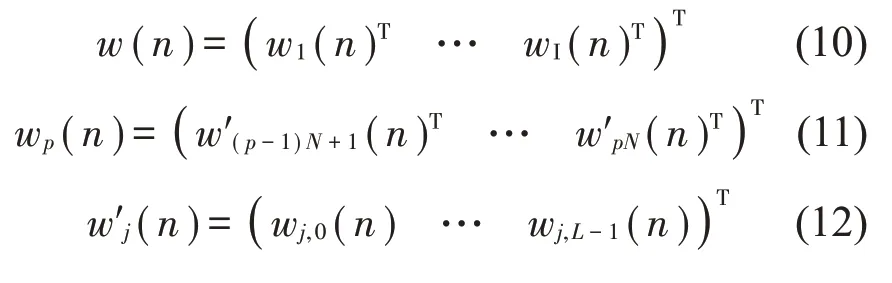
式(12)中：wj,l(n)表示與第j 個次級源相關的自適應濾波器的第l個系數。如果用w(p-1)N+j,l(n)來表示第p 個子系統中第j 個濾波器的第l 個系數，則式(5)中單個系數的迭代公式如式(13)所示。

1.2 等效傳遞函數

對式(4)等號兩側做Z變換，整理得式(14)，在此式中，上標H 表示厄米特共軛，S 為如式(15)所示的次級通路響應矩陣。

式(15)中：Sp,q表示第p個子系統的次級源到第q個子系統的誤差傳感器之間的次級通路響應矩陣，如式(16)所示。

對式(13)做Z 變換，并代入式(14)中的Wl(z)可得

式中

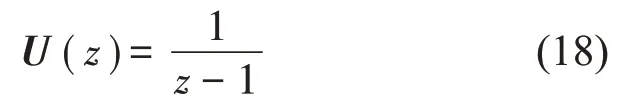
將式(17)代入式(14)，即可得到整個系統Z 變換后的方程，如式(20)所示。

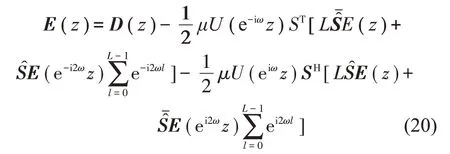
式(20)中的求和部分包含的E(e±i2ωz)部分導致整個系統的傳遞函數無法直接得出。因此這里可以進一步假設參考信號為同步采樣信號，且每L 個采樣點對應參考信號整數個信號周期[9]。在這一前提下，Lω就等于π的整數倍，因此有

這樣就去掉了式(21)中包含E(e±i2ωz)的部分，系統方程就化為

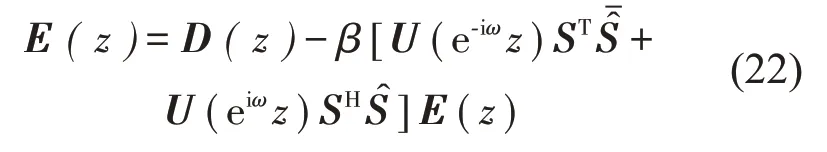
式中β稱為歸一化迭代系數，有

將式(18)代入式(22)，得到系統傳遞函數為

H(z)為NI×NI 傳遞函數矩陣，表示了每個誤差傳感器信號與所有初級噪聲之間的關系。式(24)表示集群式系統的收斂過程等價于一個反饋系統，G(z)為開環傳遞函數矩陣，β為反饋增益。

2 算例

2.1 單個子系統

首先考慮單個子系統在自由空間中的情況，假設子系統本身為一個小型的集中式系統，有2 個次級源、2 個誤差傳感器，其空間位置如圖2 所示。圖中尺寸為與波數k 相關的歸一化尺寸，即kd=1，即次級源和誤差傳感器分布在大小為1的正方形的四個頂角上。如果聲速為344 m/s，對于頻率100 Hz的信號，圖中距離1實際表示約548 mm。

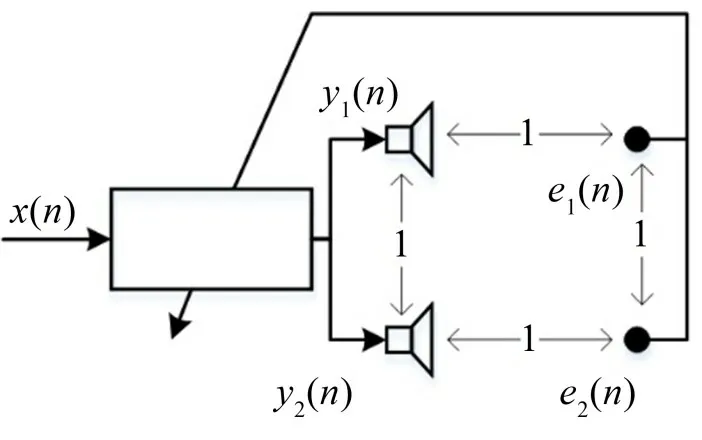
圖2 集群式系統2通道子系統

自由空間中距離為l 的2 點之間的聲耦合系數為

如果進一步假設揚聲器和傳感器電路的傳遞函數為1，則自由場中的次級通路響應矩陣為

此時傳遞函數矩陣H(z)為2×2矩陣，包含了4個傳遞函數。β 從0 變化到0.1 時，H(z)零點的變化軌跡如圖3所示，根軌跡如圖4所示，圖中“○”表示β=0時的位置，“+”表示β=0.1時的位置。

注意到，在零點圖中，隨著β的變化有共軛零點始終保持在角度±ω處的單位圓上，說明H(e-iω)=0，也就是誤差傳感器處的信號為0，這與自適應系統的穩態性能一致。

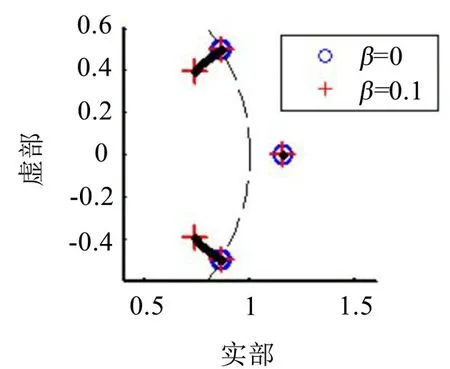
圖3 單個子系統的零點軌跡

在根軌跡圖中，隨著β的變化，極點從角度±ω處的單位圓上向圓內移動，根軌跡落在單位圓內。

說明當β=0時，極點與零點重合，H(e-iω)=1，也即誤差傳感器處的信號等于初級噪聲，系統不起控制作用，對應μ=0時自適應系統不進行迭代。當β>0時，系統極點落在單位圓內，系統處于穩定狀態。

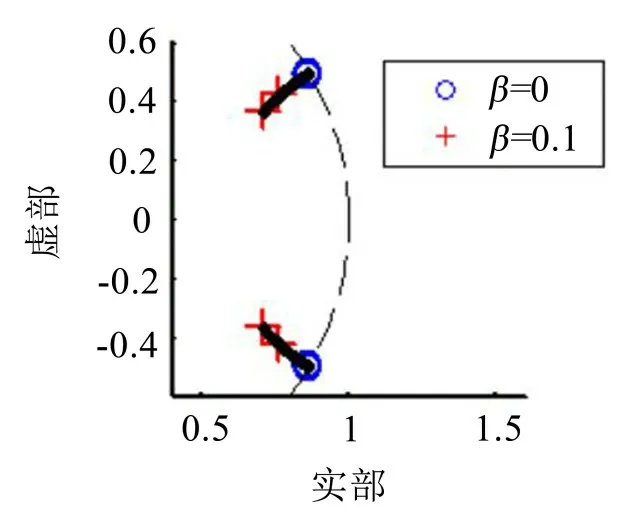
圖4 單個子系統的根軌跡

2.2 兩個子系統

假設集群式系統包含2 個2.1 小節所述的子系統，子系統在自由空間中對稱布置，子系統之間的距離為d1，如圖5所示。

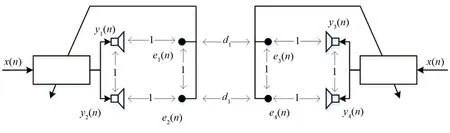
圖5 對稱布置的集群式系統

系統在不同d1下的穩定性如表1 所示，d1分別為-0.1、0、0.1和1時的誤差迭代曲線如圖6所示。

表1 集群式系統在d1不同時的穩定性

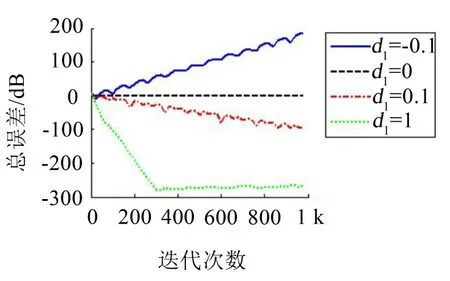
圖6 d1不同時的收斂曲線

可以看到，當d1=-0.1時兩個子系統的空間區域互相重疊，此時系統處于不穩定狀態，這種情況下系統根軌跡如圖7所示。

可以看到當β>0時，有根軌跡落在單位圓外，這解釋了在這種情況下系統不穩定的原因。

圖7 d1=-0.1時系統根軌跡分布

當d1=0時，系統處于臨界穩定狀態，此時系統傳遞函數H(z)在ω 處的響應如式(28)所示。可以看到式中矩陣每行有2個傳遞函數的幅度響應為0.5，這使得每個誤差傳感器的總響應均為1，即系統既不收斂，也不發散，處于臨界穩定狀態。

如圖8 所示，在d1>0 時隨著β 從0 改變到0.1，d1取值0.1和1時系統的根軌跡均落在單位圓內，因此此時系統均是穩定的，且圖8(a)所示d1=0.1的根軌跡比圖8(b)d1=1的根軌跡更靠近單位圓，這解釋了d1=1時系統誤差收斂的速度快于d1=0.1時的原因。

不同d1取值對收斂速度的影響如圖9所示。結合圖6 來看，隨著d1從0 開始增加，系統誤差的收斂速度不斷增加，同時收斂速度的增加速度不斷降低，當d1>0.5時，收斂速度的增加已經可以忽略了。

當d1很大時（如100），整個系統的零極點已經和第2.1小節的單個子系統保持一致，也就是說由于子系統之間距離很大，子系統之間的相互影響與自身次級源對誤差傳感器的影響相比已經可以忽略不計。

圖8 d1>0時系統的根軌跡分布

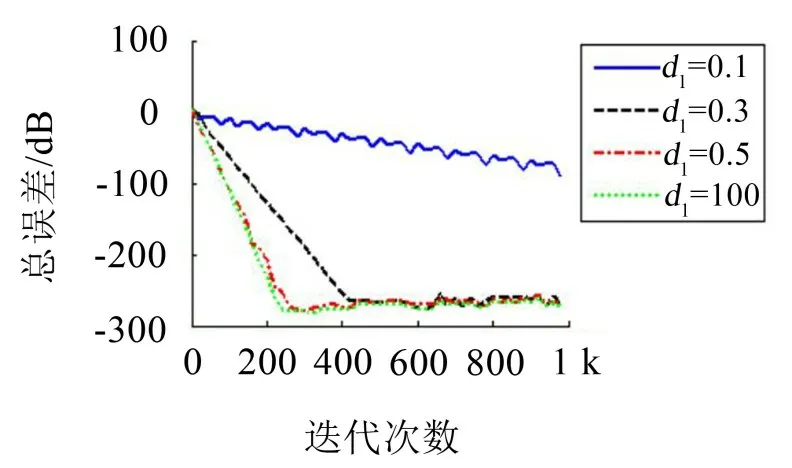
圖9 隨著d1增大系統收斂曲線的變化

3 結語

本文對集群式有源噪聲控制系統在控制單頻噪聲時的迭代公式進行Z 變換，推導得到等效傳遞函數。對系統等效傳遞函數的零極點圖進行分析能預測系統穩定性和穩態誤差，后續對單個子系統的仿真驗證了理論推導的正確性。

考慮最簡單的情況，假設集群式系統包含2 個對稱放置的子系統。仿真結果表明，當2 個子系統的空間區域互相重疊，也就是距離小于0時，由于根軌跡分布在單位圓外，系統處于不穩定狀態；當距離0時，系統處于臨界穩定狀態，此時等效傳遞函數中每個誤差傳感器的幅度響應為1，也就是說系統無效。如果要集群式系統有效，兩個子系統之間的距離應至少大于0.5。因為如果距離小于0.5，此時系統雖然仍能保持穩定，但子系統之間的互相影響將強到導致誤差收斂速度顯著減慢，而相反地，如果距離大于0.5，子系統之間的互相影響就減弱到可以接受的程度，此時系統必定處于穩定狀態，且有最佳的誤差收斂速度。

由上述分析可以得出結論，集群式系統子系統的空間布放對系統穩定性有重要影響，子系統之間的互相影響越大，系統越接近不穩定狀態，誤差收斂速度越慢，反之亦然。總的來說，集群式系統的空間布放應滿足以下兩個原則：

(1)子系統的次級源和誤差傳感器應緊密布放，增大自身次級源對自身誤差傳感器的影響能力；

(2)盡可能減少子系統之間的互相影響，至少應使其至少小于子系統自身次級源對誤差傳感器的影響。