基于TS-MMPF的機動弱目標TBD算法*

譚順成，于洪波

（海軍航空大學信息融合研究所，山東 煙臺 264001）

0 引言

檢測前跟蹤（Track-Before-Detect，TBD）算法[1-12]是一種低信噪比情況下對目標進行檢測和跟蹤的有效方法。目前，典型的TBD算法主要包括Hough變換[2-3]、最大似然[4]和動態規劃[5-6]以及粒子濾波（Particle Filter，PF）[7-12]等方法。其中，基于 PF 的TBD算法因對非線性非高斯系統具有較好的適應性，是目前研究的熱點，基于多模粒子濾波（Multiple Model Particle Filter，MMPF）[7]的 TBD 的算法就是檢測機動弱目標的典型代表。然而基于MMPF的方法，一方面只是在每個時刻給出了目標狀態的估計值，不能給出目標的航跡信息；另一方面，當粒子出現嚴重退化時，粒子的多樣性急劇減少，粒子集比較單一，容易造成存在卻檢測到目標不存在的問題，即目標漏檢。

本文立足于解決此類問題，在基于MMPF的TBD方法基礎上，提出一種基于航跡平滑（Track Smoothing，TS）的MMPF（TS-MMPF）機動弱目標TBD算法，該方法對MMPF的輸出結果進行航跡起始、關聯及濾波，當檢測目標不存在時利用航跡預測值代替估計值，對目標航跡進行平滑形成暫定航跡，最后借助后續時刻的估計值判斷是否維持或撤銷暫定航跡，有效克服因粒子退化造成的目標漏檢問題，提高了目標航跡的穩健性。

1 系統模型

1.1 狀態模型

考慮單目標在x-y二維平面機動運動的場景，并假設在任意觀測時間內目標的運動模式服從勻速直線運動、順時針坐標轉動以及逆時針坐標轉動3種模式中的一種，以表示3種運動模式集合，其中，1代表勻速直線運動，2代表順時針坐標轉動，3代表逆時針坐標轉動。以表示目標狀態，其中，和Ik分別表示目標位置、速度和強度狀態，目標狀態轉移方程為

式（3）對應于坐標轉動模式

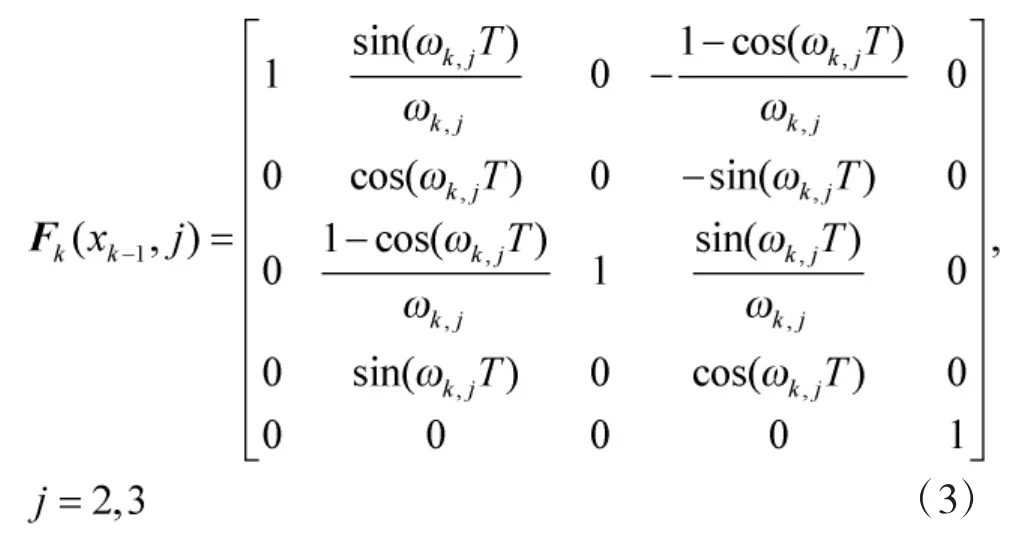
式中，T為傳感器掃描周期，另外

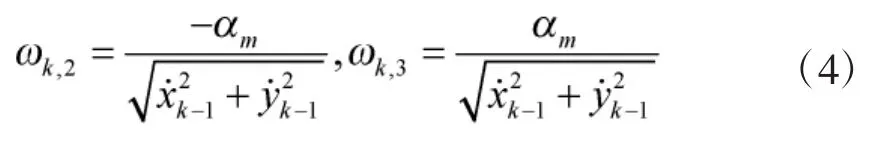
分別對應于順時針坐標轉動和逆時針坐標轉動，αm＞0是一個典型的機動加速度。

假設mk作用于時間段，目標某一時刻只遵循一種運動模式，整個運動過程中，各種運動模式之間的轉換可描述為3態的1階Markov鏈。模式轉移概率矩陣∏m，其各元素

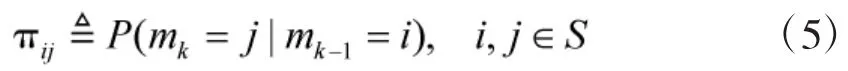
k時刻目標可能存在于傳感器警戒區域內，也可能不存在，以變量Ek對此建模。描述為2態的1階Markov鏈，即。0表示目標不存在，1表示目標存在。并定義目標“新生”概率Pb和“死亡”概率Pd為

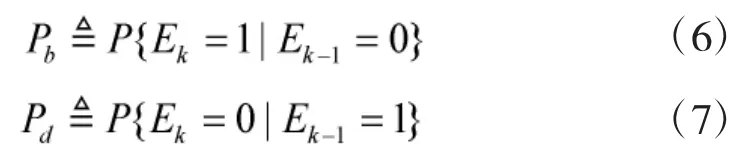
其轉換概率矩陣為

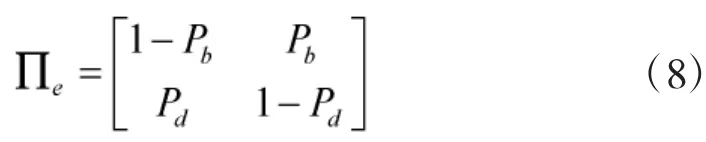
1.2 量測模型

假設傳感器提供的監控區域內的二維圖像，每張圖像包含m×n個分辨單元。每個分辨單元對應于一個的區域，第（i，j）個單元的中心定義為。以表示時刻k

分辨單元（i，j）的觀測數據

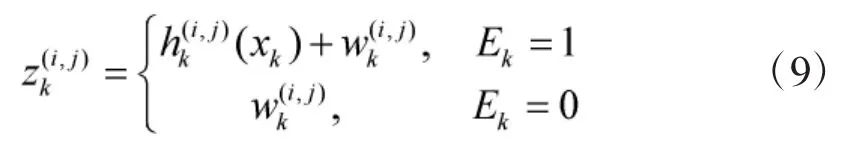
其中

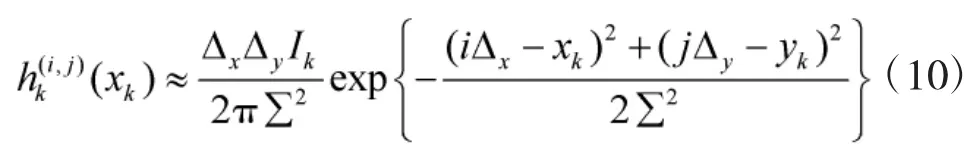
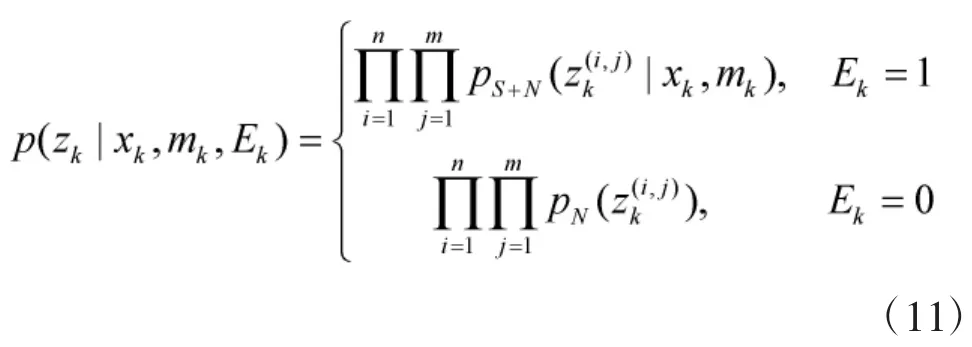
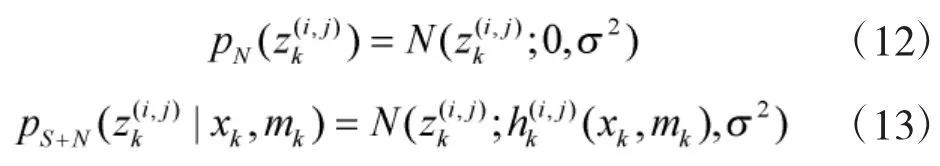
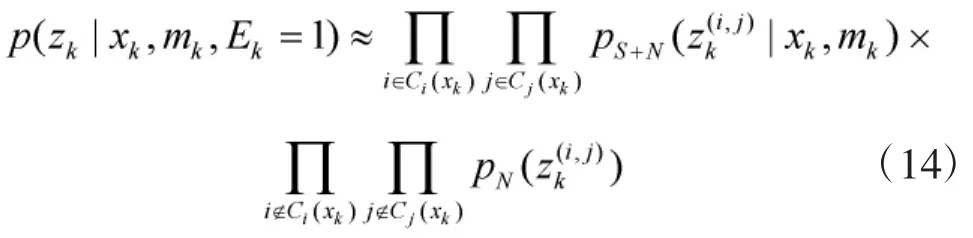
2 算法實現

2.1 濾波器初始化

5）根據目標初始運動模式概率φ0初始化目標運動模式變量；

2.2 粒子集預測

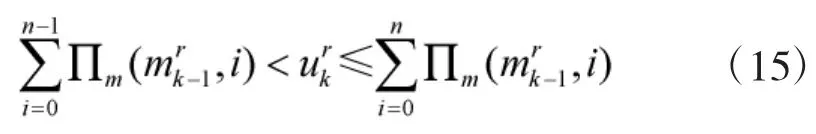
② 根據目標初始運動模式概率φ0生成預測的目標運動模式變量；

3）將對“持續存在”粒子進行預測得到的粒子集和“新生”粒子集進行合并，得到總的預測粒子集。

2.3 粒子權重更新和重采樣

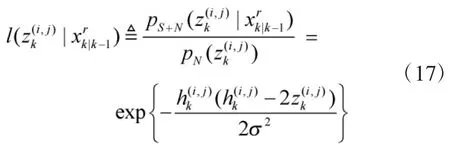
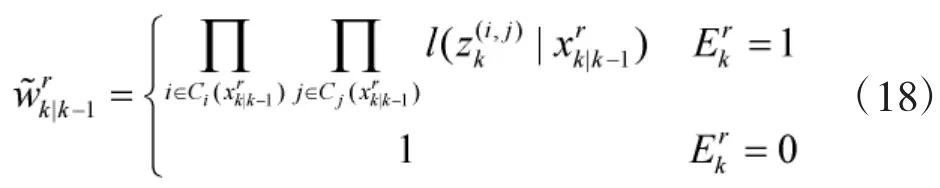
2）歸一化粒子權重

2.4 目標狀態估計和航跡平滑

計算目標存在概率

① 設置目標存在標志flag=2；

② 估計目標狀態

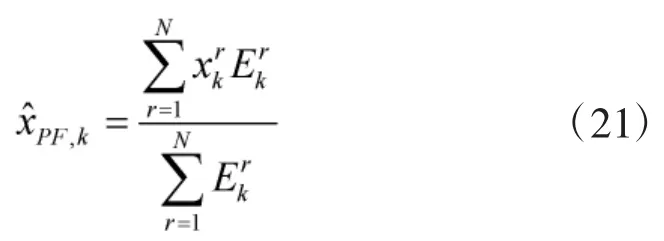
及狀態協方差

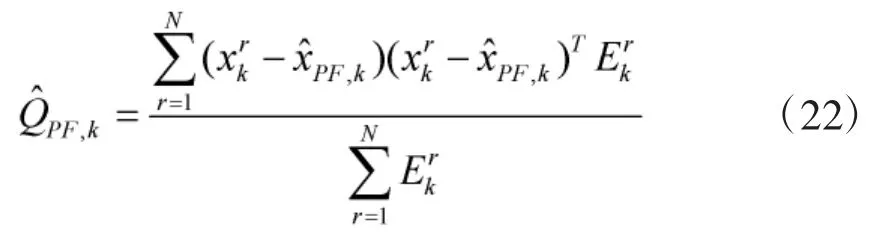
③ 估計目標按各模式運動的概率

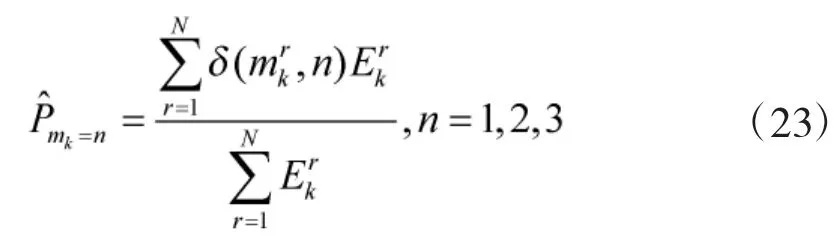
及當前時刻目標的運動模式

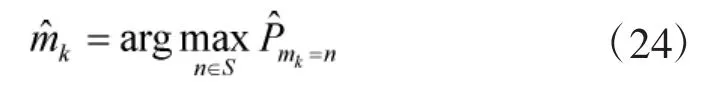
其中

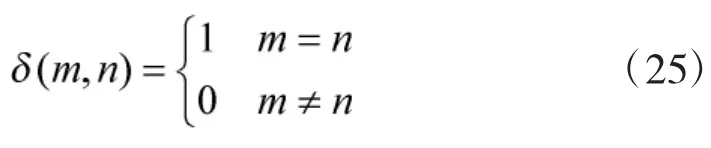
③若flag＜0，當前時刻沒有目標航跡，令flag=0。

基于TS-MMPF機動弱目標TBD算法的基本流程如下頁圖1所示。

3 實驗仿真

設置一個與文獻[8]相同的仿真場景，進行實驗仿真，仿真總時間為45 s，其中目標從第7 s開始出現，首先沿x軸方向作10 s勻速直線運動，接著作5 s逆時針轉彎運動，此后進入10 s的勻速直線運動，最后作5 s的順時針機動轉彎，直到37 s消失，一共存在30 s。假設過程噪聲w為零均值高斯白噪聲，其協方差矩陣為

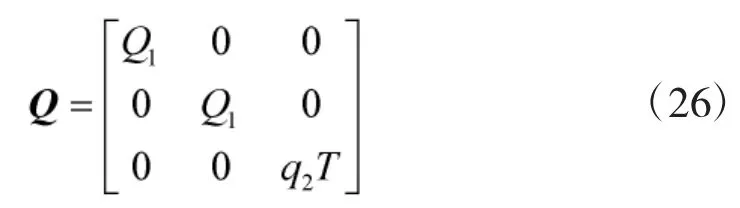
其中

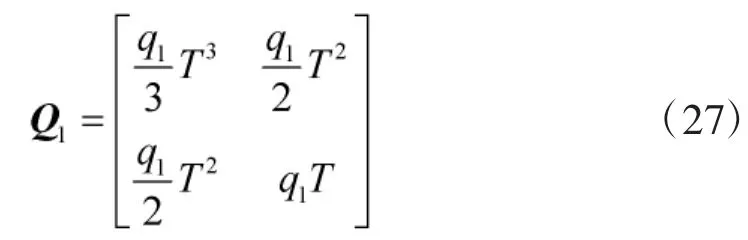
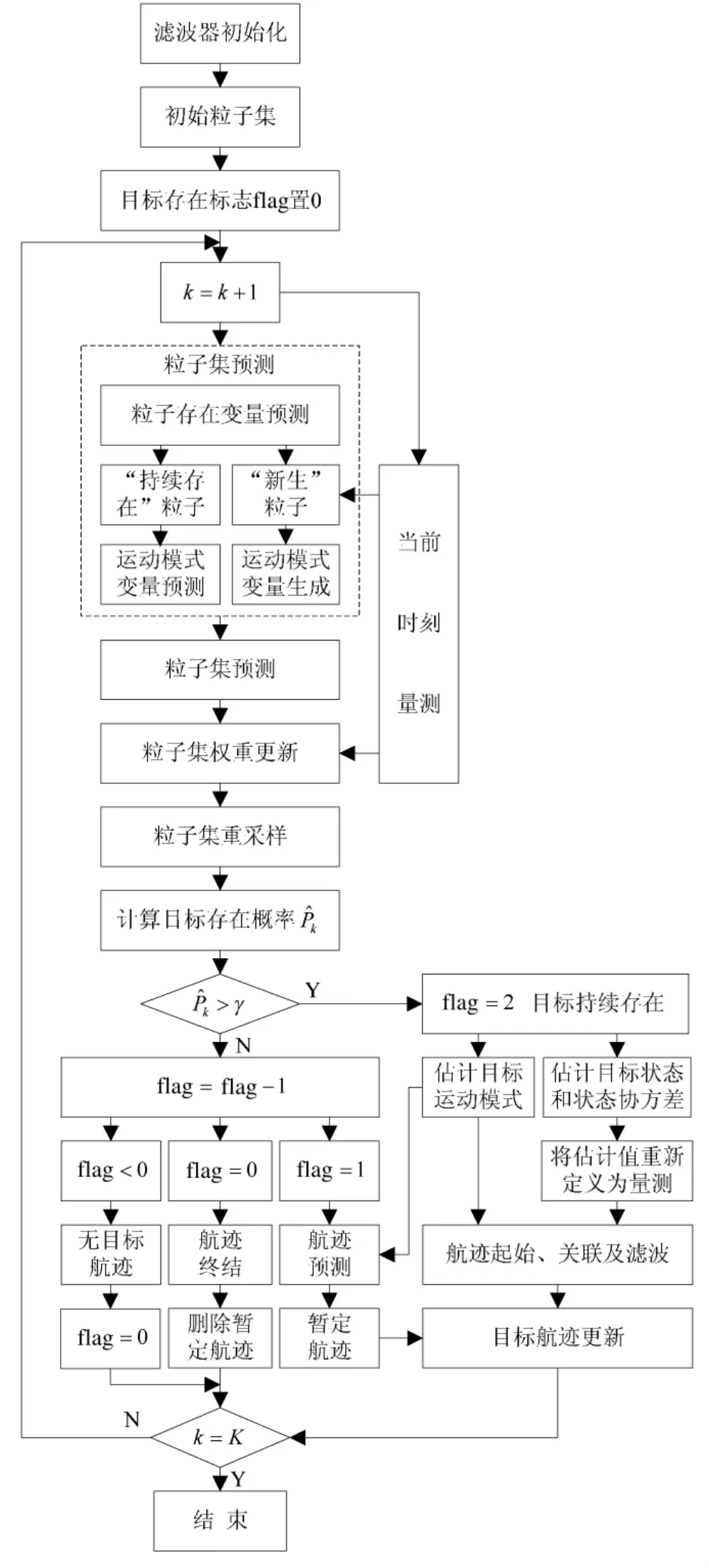
圖1 算法流程圖

q1和q2分別表示目標運動狀態和目標強度的過程噪聲。仿真中設置為q1=0.001，q2=0.01，機動加速度αm=1.08，傳感器采樣間隔T=1 s，每一秒產生一幀觀測圖像。觀測區域m×n為60×60，每一個分辨單元的尺度設置為 Δx=Δy=1。目標初始位置為（20，20），速度為（2，0）分辨單元每秒。目標初始存在概率，“新生”粒子3種運動模式概率分別為 φ1=0.9，φ2=0.05，φ3=0.05，持續存在粒子的運動模式轉移概率矩陣[8]為

圖2為信噪比為6 dB時傳感器得到的4幀（第1幀、7幀、20幀和38幀）量測數據的灰度圖，由仿真場景設置可知，第1幀和38幀目標實際不存在，第7幀和第20幀目標實際存在，但是由于信噪比較低，目標回波信號湮沒在噪聲信號里，并不能從這些量測數據直接判斷出目標是否存在，更不能直接獲得目標的位置信息。

圖2 SNR=6 dB時的4幀量測數據灰度圖

圖3～圖6分別給出了目標信噪比為6 dB時基于MMPF和本文TS-MMPF的TBD算法的仿真結果，其中圖3和圖4分別為基于MMPF估計目標存在概率（底部的“*”號表示當前時刻目標實際存在于監控區域內）和估計的目標點跡與真實的目標航跡對比，圖5和圖6分別為TS-MMPF估計的目標存在概率和目標航跡與真實的目標航跡對比。

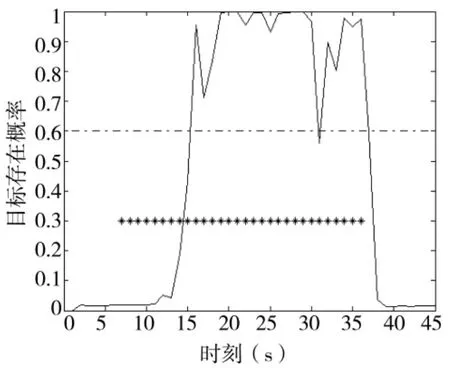
圖3 MMPF估計的目標存在概率

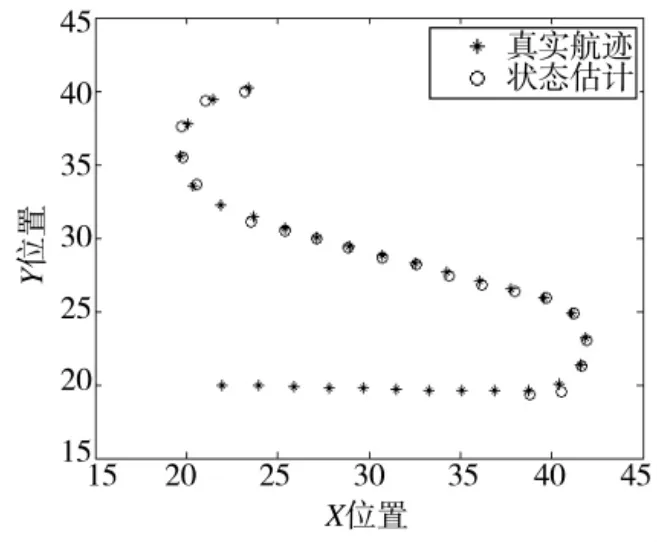
圖4 MMPF估計的目標點跡和真實目標航跡對比

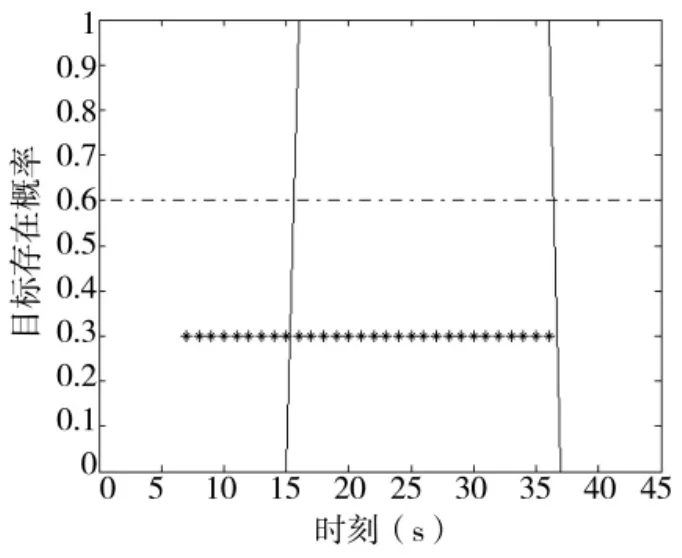
圖5 TS-MMPF算法估計目標存在概率

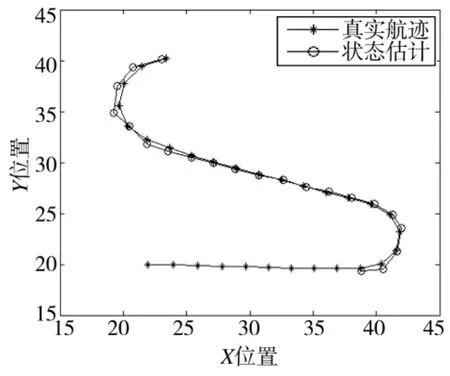
圖6 TS-MMPF算法估計的目標航跡與真實航跡對比

由圖4和圖5比較可以看出，經過一段時間的積累后，MMPF僅給出了估計的目標點跡，不能給出目標的航跡信息，而本文的TS-MMPF算法可以直接給出目標航跡。圖3 MMPF估計的目標存在概率存在一定的起伏，如果設置判斷目標是否存在的檢測門限為0.6，從圖3可以看出，MMPF算法在第7 s～第16 s以及第31 s出現了目標漏檢（同時體現圖4的相應時刻不能給出目標狀態估計值），其中第7 s～第16 s因為目標信噪比較低，算法積累不夠而未檢測到目標，而第31 s卻是因為粒子退化而出現的目標漏檢；圖5 TS-MMPF算法給出的估計目標存在概率不存在起伏，同時有效修補了第31 s出現的目標漏檢，并給出了該時刻的目標狀態估計，因此，本文算法可以有效地提供目標航跡信息，提高目標航跡的穩健性。

4 結論

為解決基于MMPF的TBD方法存在不能直接給出目標航跡，以及粒子嚴重退化時容易出現目標漏檢等問題，提出一種基于TS-MMPF機動弱目標TBD算法。在對多目標進行檢測跟蹤時，往往需要知道各目標的航跡信息，即各時刻各狀態估計值與前后時刻各狀態估計值之間的關系，也就是狀態值之間的關聯問題，本文為基于PF類的TBD算法只能給出目標狀態而不能給出目標航跡信息的問題提供了一種可行解決思路，下一步將針對該算法推廣應用于多微弱目標的檢測與跟蹤情況，進一步增強算法的適應性。此外，如何有效縮短算法的積累時間，減小目標檢測延滯也將是需要研究的難點問題。