Galerkin法求解彈性邊界條件下圓板的流-固耦合振動特性

陳美霞， 姚仕輝， 謝 坤

(華中科技大學 船舶與海洋工程學院，武漢 430074)

圓板作為常見的結構單元，在工程上有著廣泛的應用。在很多情況下，圓板是與流體接觸的，如微量泵、蝶閥的圓盤、整體式核反應堆的冷卻劑等。流體的存在會顯著降低圓板的固有頻率，從而改變結構的動力響應特性，因此對圓板和流體的流-固耦合問題進行研究具有重要意義。

Kwak[1]研究了漂浮在無限流域上圓板的振動特性，通過引入無量綱附加質量因子(NAVMI)來評價流體對于圓板的作用，近似求解了圓板的固有頻率。后來，Kwak[2]應用Hankel變換計算了嵌在剛性障板中圓板的水動力特性，通過與文獻[1]進行比較，發現嵌在剛性障板中的圓板所受到的流體附加質量作用比漂浮在自由液面上的圓板更大。Kwak等[3]求解了漂浮在深度有限的流體上圓板的振動特性，并分析了深度改變對于圓板固有頻率的影響。Kwak等通過NAVMI法求解圓板的固有頻率時，忽略了流體對圓板振型的影響，因此計算結果有一定誤差。Amabili等[4]在考慮流體對結構振型影響的基礎上，通過Rayleigh-Ritz法建立控制方程，更精確地求解了結構的固有頻率，并與NAVMI法進行對比，結果表明，采用NAVMI法求解低階頻率時誤差較小。Bauer[5]研究了彈性薄膜封蓋或彈性薄板封蓋與容器內流體的耦合振動，結果表明，封蓋與流體耦合振動的固有頻率會大于沒有封蓋時流體的晃動頻率。Bauer等[6]在Bauer的研究基礎上，考慮了流體粘性的影響。Amabili[7]研究了漂浮在容器內流體表面的圓板的振動特性，分析了自由液面表面波對于圓板振動的影響。在文獻[7]的基礎上，Yousefzadeh等[8]分析了漂浮在自由液面上的功能梯度圓板的振動特性。Cheung等[9]研究了作為開口容器底部結構的彈性圓板的水動力特性，利用疊加原理將自由液面邊界條件分離出來，分析了流體自由表面波對圓板振動的影響。Jeong等[10]研究了充滿可壓縮流體的封閉容器中圓形隔板的振動特性，分析了流體壓縮性對于圓板振動特性的影響。Askari等[11]對浸沒在開口容器中的圓板的振動特性進行分析，并考慮了液體晃動的影響。Eftekhari[12]引入微分求積法(DQM)求解了圓板的流-固耦合振動問題。Tariverdilo等[13]分別用Fourier-Bessel級數法和變分法分析了圓板的流-固耦合問題，并對比了不同方法的計算結果，但未涉及軸對稱模態的計算。Jeong[14]計算了完全相同的兩塊圓板與流體的耦合振動，分別求解了耦合系統的同相和反相模態。在求解軸對稱模態時，Jeong對附加質量矩陣的元素進行了修正，但反相軸對稱模態結果的誤差仍相對較大。

基于文獻[13-14]，本文結合Fourier-Bessel級數展開法和Galerkin法建立控制方程，對與流體接觸的邊界彈性約束圓板的固有振動特性進行了研究。利用0階貝塞爾函數的性質，添加附加約束方程，對軸對稱模態進行求解。在此基礎上分析了彈簧剛度和流體深度對于圓板自由振動的影響。

1 理論分析

1.1 圓板位移的級數表達

如圖1所示，圓柱形容器內充滿不可壓縮的無黏性流體，容器底面和柱面為剛性壁面，頂面覆有彈性圓板。流體密度為ρ0，深度為d；圓板半徑為a，板厚為h，圓板邊緣設有均勻分布的位移彈簧和轉角彈簧，彈簧的分布剛度分別為K和Kφ。

假設圓板滿足基爾霍夫薄板理論，則系統的動力平衡方程可表示為

(1)

式中：w，D，ρ分別為板的撓度、彎曲剛度和密度，P為流體壓力，▽4為柱坐標系下的雙調和算子，其表達式為

(2)

根據模態正交性理論，圓板位移可以展開為真空中振型的級數：

(3)

圖1 與流體接觸的邊界彈性約束圓板Fig.1 Elastically restrained circular plate in contact with fluid

式中：Wnm為圓板在真空中的振型，qnm為廣義坐標，n和m分別為節徑數和節圓數。Wnm滿足式(1)對應的齊次微分方程：

(4)

根據文獻[15]可知，圓板在真空中的振型為：

Wnm(r,θ)=[Jn(λnmr)+

CnmIn(λnmr)]cos(nθ)

(5)

式中：Jn和In分別為n階第一類貝塞爾函數和第一類修正貝塞爾函數。Cnm為與振型有關的系數，λnm為頻率系數，滿足

(6)

式中：ωnm表示真空中圓板的固有頻率。

當圓板材料和尺寸一定時，振型系數Cnm和頻率系數λnm取決于彈簧剛度K和Kφ，系數的求解步驟見附錄A。由此可知，當圓板邊界條件確定時，真空中的振型Wnm為已知函數，只要求解出廣義坐標qnm，即可根據式(3)得到圓板在流體中的振型。

1.2 流體速度勢函數

假設流體作無旋運動，則可用速度勢函數Φ(r,θ,x,t)描述流體運動。結合1.1節中流體不可壓縮且無粘性的假設，Φ(r,θ,x,t)滿足拉普拉斯方程：

▽2Φ=0

(7)

將速度勢函數的時間項和空間項分離，可得[14]

Φ(r,θ,x,t)=iωφ(r,θ,x)eiωt

(8)

式中：φ為空間速度勢函數，且同樣滿足拉普拉斯方程。應用分離變量法可得，對于某一個確定的節徑數n，φ的一般解為(參考附錄B)：

φ(r,θ,x)=(anx+bn)δn0cosnθ+

Fnscosh(βnsx)]cosnθ

(9)

式中：δn0是Kronecker delta函數，an、bn、Ens、Fns、βns為待求系數，且βns>0。

由于容器柱面和底面為剛性壁面，φ需要滿足如下邊界條件：

(10)

(11)

將式(9)代入(10)，可以得到關于βns的方程：

(12)

同理，將式(9)代入(11)，可得

a0=0

(13)

Ens=0

(14)

因此，式(9)可以簡化為

φ(r,θ,x)=cosnθ[b0δn0+

(15)

1.3 流-固耦合面處的連續性條件

在流-固耦合面，需要滿足圓板和流體的速度連續性條件：

(16)

將式(3)、(8)和(15)代入式(16)可得

(17)

其中Rnm(r)=Jn(λnmr)+CnmIn(λnmr)為干圓板振型的徑向分量。根據貝塞爾方程本征函數的正交性[16]，在方程(17)左右兩邊乘以rJn(βnsr)，并在[0,a]積分可得

(18)

當n=0時，常數函數也是貝塞爾方程的本征函數，且對于?β0s>0，常數函數與J0(β0sr)在[0,a]帶權r正交。在方程(17)兩邊同時乘以r并在[0,a]積分，可得n=0時還需要滿足的附加約束方程：

(19)

將式(18)代入(15)，速度勢函數φ可以進一步表示為

φ(r,θ,x)=cosnθ[b0δn0+

(20)

其中

(21)

1.4 控制方程求解

假設圓板作小振幅振動，應用線性伯努利方程可得作用于圓板的流體壓力：

(22)

此時對于確定的n，平衡方程可以表示為

(23)

應用Galerkin法，在方程(23)兩邊乘以Wnk(r,θ)并在圓板范圍積分，結合真空中振型的正交性[15]可得代數方程：

(24)

分別取m和s的截斷數為M和S，可以將式(24)寫成矩陣形式。當n>0時，式(24)可表示為

[ρhPn-ω2(ρhZn+ρ0Gn)]qn=0

(25)

其中qn={qn0,qn1,…,qnM}T為系數向量，Pn,Zn,Gn為M+1階矩陣，各矩陣元素分別為

(26)

(27)

k,m=0,1,2,…,M

(28)

當n=0時，除系數向量q0外b0也是未知量，為求得b0和q0，代數方程組(24)需要和附加約束方程(19)聯立求解，表示成矩陣形式分別為

[ρhP0-ω2(ρhZ0+ρ0G0)]q0-ρ0ω2c0b0=0

(29)

l0q0=0

(30)

式中：P0,Z0,G0和q0與n>0的情況有著相同的表達式。c0和l0分別為M+1維的列向量和行向量，其元素分別為

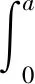
(31)

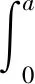
(32)

此時n=0時的控制方程可以表示為如下矩陣形式：

(33)

式(25)和(33)給出了矩陣形式的控制方程。要使方程存在非平凡解，必須讓系數矩陣的行列式為零，由此求解出的ω即為與流體接觸的圓板的固有頻率；求出對應的非零解即可得廣義坐標qnm，代入式(3)可得圓板在流體中的振型。

2 數值計算與結果分析

2.1 方法驗證

為驗證本文解析方法的正確性，將基于本文解析方法的計算結果與基于有限元法的數值結果進行對比。計算時采用如下參數：圓板半徑a=0.2 m，板厚h=0.002 m，密度ρ=2 700 kg/m3，楊氏模量E=69 GPa，泊松比ν=0.3；流體密度ρ0=1 000 kg/m3，深度d=0.02 m；位移彈簧的分布剛度K=103N/m2，轉角彈簧的分布剛度Kφ=103N/rad。本文方法采用Matlab實現，截斷數M和S均取40。數值結果采用有限元軟件Ansys得到，其中圓板采用Shell63單元，流體采用Fluid30單元，網格尺寸取Δ=0.004 m。

對截斷數M和S的收斂性分析如表1所示。由表1可知，在保留兩位小數時，截斷數取40和50的計算結果是一致的，而截斷數取30時部分高階頻率尚未收斂，故取截斷數M=S=40是合理的。

表1選取不同截斷數M和S求得的圓板固有頻率

Tab.1Naturalfrequenciesofthecircularplateobtainedbyusingdifferenttruncationnumber

nm固有頻率/HzM=S=30M=S=40M=S=5001118.63118.63118.632646.26646.26646.2631 697.141 697.141 697.141011.6111.6011.601305.95305.94305.9421 085.351 085.351 085.3532 409.992 409.992 409.992058.1958.1958.191577.72577.72577.7221 618.651 618.651 618.6533 220.713 220.703 220.7030153.58153.58153.581932.13932.13932.1322 242.582 242.572 242.5734 126.834 126.824 126.82

為驗證有限元網格的收斂性，分別對Δ1=0.008 m，Δ2=0.004 m，Δ3=0.002 m三種網格尺寸的有限元模型進行分析，計算結果如表2所示。表中f1、f2、f3為不同模型的固有頻率，e1、e2為相對誤差，滿足e1=(f1-f2)/f2，e2=(f2-f3)/f3。由于有限元網格收斂較慢，在綜合考慮計算速度和精度的條件下，本文以相對誤差<1%作為有限元網格收斂的評判標準，結合表2的結果，取網格尺寸Δ=Δ2=0.004 m是合理的。

表2采用不同網格尺寸的有限元模型得到的圓板固有頻率

Tab.2NaturalfrequenciesofthecircularplateobtainedbyFEMusingdifferentmeshsize

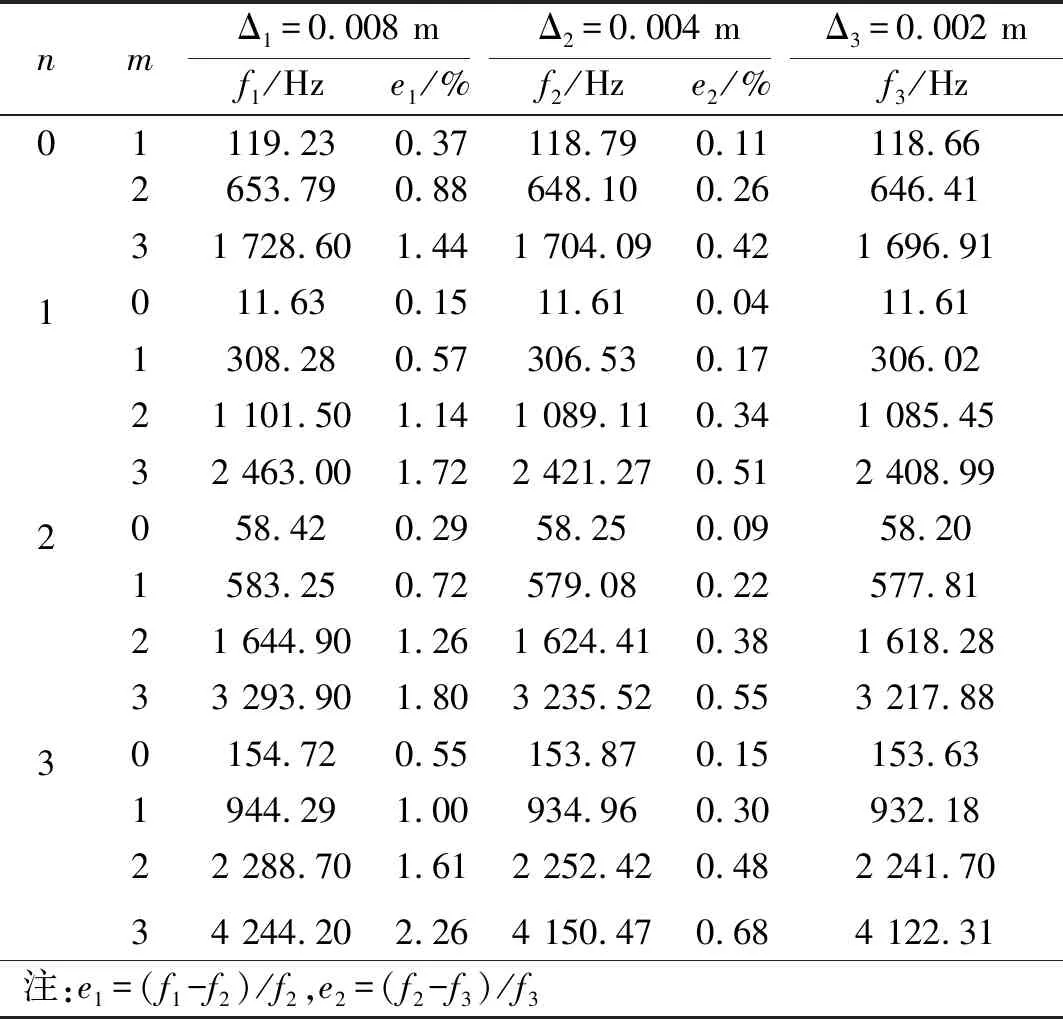
nmΔ1=0.008 mΔ2=0.004 mΔ3=0.002 mf1/Hze1/%f2/Hze2/%f3/Hz01119.230.37118.790.11118.662653.790.88648.100.26646.4131 728.601.441 704.090.421 696.911011.630.1511.610.0411.611308.280.57306.530.17306.0221 101.501.141 089.110.341 085.4532 463.001.722 421.270.512 408.992058.420.2958.250.0958.201583.250.72579.080.22577.8121 644.901.261 624.410.381 618.2833 293.901.803 235.520.553 217.8830154.720.55153.870.15153.631944.291.00934.960.30932.1822 288.701.612 252.420.482 241.7034 244.202.264 150.470.684 122.31注:e1=(f1-f2)/f2,e2=(f2-f3)/f3

分別采用本文方法和有限元法求得的圓板固有頻率結果如表3所示。從表中可知，對于n,m=0,1,2,3的模態，本文方法與有限元法計算結果相對誤差在1%

表3本文方法與有限元法求得的固有頻率結果對比

Tab.3ComparisonofthenaturalfrequenciesobtainedbypresentmethodandFEM

nm有限元法/Hz本文方法/Hz相對誤差/%01118.79118.63-0.132648.10646.26-0.2831 704.091 697.14-0.411011.6111.60-0.051306.53305.94-0.1921 089.111 085.35-0.3532 421.272 409.99-0.472058.2558.19-0.111579.08577.72-0.2421 624.411 618.65-0.3533 235.523 220.70-0.4630153.87153.58-0.191934.96932.13-0.3022 252.422 242.57-0.4434 150.474 126.82-0.57

以內，驗證了本文方法的正確性。此外，由表3還可以看出隨著節徑數n和節圓數m的增加，圓板的固有頻率變大。需要注意的是，本文假定流體不可壓縮，因此流體體積保持不變，故不存在n=m=0的模態。

2.2 圓板與流體的耦合振動特性分析

2.2.1 彈簧剛度對圓板自由振動特性的影響

(a) 自由(K=0, Kφ=0)

(c) 導向(K=0, Kφ=∞)

(d) 固支(K=∞, Kφ=∞)圖2 不同邊界條件下圓板的無量綱頻率Fig.2 Nondimentional frequencies of circular plates with different boundary conditions

流體不僅會降低圓板的固有頻率還會改變圓板的振型，圖3給出了圓板在真空中和流體中的歸一化振型的對比。由圖3看出，簡支和固支圓板的振型受到流體的影響相對較大，自由邊界圓板的振型受到流體影響很小，導向邊界圓板在真空中和流體中的振型幾乎完全一致。

(a) n=0,m=2自由

(b) n=1,m=2自由

(c) n=0,m=2簡支

(d) n=1,m=2簡支

(e) n=0,m=2導向

(f) n=1,m=2導向

(g) n=0,m=2固支

(h) n=1,m=2固支圖3 圓板在真空中和流體中的歸一化振型Fig.3 Normalized mode shapes of the circular plate in vacuo and in fluid

在求解固有頻率時，若忽略流體對振型的影響，采用圓板在真空中的振型代替圓板在流體中的振型進行求解，即假定w(r,θ)=Wnm(r,θ)，式(23)可簡化為

(34)

當n>0時，式(34)兩邊乘以Wnm在[0,a]積分可以直接求出固有頻率ω，相對于求解矩陣方程(25)的廣義特征值問題，將大為減少計算時間。

而對于n=0，式(19)簡化為

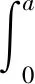
(35)

此式無法成立，因此在求解軸對稱模態(n=0的模態)時，這種簡化方法是不適用的。

利用式(34)解出的圓板固有頻率如表4所示，表中括號中結果為通過求解式(25)的廣義特征值問題得到的固有頻率。由表4可知，對于自由和導向邊界圓板，忽略流體對振型的影響對圓板固有頻率的計算結果影響較小，誤差在5%以內；而對于簡支和固支圓板，則會產生較大的誤差。由圖3的結果可知，這是因為自由和導向邊界圓板振型受到流體影響更小，采用近似方法計算時假定振型(真空中的振型)與真實振型(流體中的振型)很接近，因此誤差較小。從表4還可以看出，對于以上四種邊界條件，當周向波數n增加時，近似解法的誤差會降低。由此可知，當邊界條件為自由、導向或者當所求模態周向波數n較大時，可以忽略流體對振型的影響。

表4 忽略流體對振型影響求得的圓板固有頻率Tab.4 Natural frequencies of the circular plate obtained by neglecting the fluid influences on mode shapes

2.2.2 流體深度對圓板自由振動特性的影響

出現上述結果是由于底部剛性壁面會限制流體的垂向運動，且距離剛性底面越近，流體作垂向運動越困難。而圓板受到流體的附加質量取決于流-固耦合層附近流體的運動情況，深度d越小，流-固耦合層附近的流體距離剛性底面越接近，運動越困難，流體隨圓板振動時需要圓板提供更大的作用力，反過來說圓板受到流體的作用力也就越大，附加質量也就越大。

(a) n=0

(b) n=1

(c) n=2

(d) n=3圖4 流體深度對無量綱頻率的影響Fig.4 The influence of fluid depth on nondimentional frequencies

3 總 結

(1) 本文采用Fourier-Bessel級數法和Galerkin法，研究了與流體接觸的邊界彈性約束圓板的自由振動特性。針對軸對稱模態，利用0階貝塞爾函數的性質，添加附加約束方程進行求解。本文方法與數值法結果吻合良好，驗證了本文計算方法的正確性。

(2) 通過改變彈簧剛度研究了幾種常見邊界條件下圓板的流-固耦合振動特性。結果表明，流體作用會降低圓板的固有頻率，且對低階模態影響更大，此結論對于不同邊界條件的圓板均成立。此外，流體還會影響圓板的振型，其中簡支和固支邊界圓板的振型受流體影響較大，而自由及導向邊界圓板的振型受到流體影響較小，針對后兩種邊界條件，可以用圓板在真空中的振型代替圓板在流體中的振型簡化計算，且這種簡化具有較高的精度。

(3) 在較低的深度范圍內，增大流體深度會顯著降低流體對于圓板的附加質量作用；當深度大于1.5倍圓板半徑時，流體深度的改變對于圓板自由振動的影響可以忽略。

(36)

(37)

式中：Mr、Nr和Mrθ分別代表單位長度的彎矩、剪力和扭矩，這三種分布內力的表達式為：

(38)

(39)

(40)

式中：ν為圓板的泊松比。將式(38)～(40)和圓板位移表達式(3)代入式(36)和(37)可得：

h1(λnm)+Cnmh2(λnm)=0

(41)

y1(λnm)+Cnmy2(λnm)=0

(42)

式中：h1(λnm),h2(λnm),y1(λnm)和y2(λnm)為關于λnm的函數，其表達式為：

(43)

(44)

(45)

(46)

聯立式(41)和(42)并消去Cnm，可得真空中圓板的頻率方程：

h1(λnm)y2(λnm)-h2(λnm)y1(λnm)=0

(47)

由式(47)可解得頻率系數λnm, 將λnm代入式(41)即可得到振型系數Cnm：

(48)

附錄B流場拉普拉斯方程求解

對空間速度勢函數φ(r,θ,x)采用分離變量法：

φ(r,θ,x)=R(r)Θ(θ)X(x)

(49)

將式(49)代入拉普拉斯方程，并在方程兩邊同時除以R(r)×Θ(θ)X(x)，可得

(50)

由于r,θ,x為相互獨立的變量，式(50)成立的條件為方程兩邊等于常數：

(51)

其中μ為常數。可得X(x)滿足微分方程：

X″+μX=0

(52)

同時，由式(51)可得

(53)

其中λ為常數。考慮到φ(r,θ,x)在周向以2π為周期，Θ(θ)滿足定解條件：

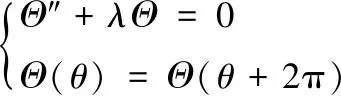
(54)

由方程(54)可求得常數λ和函數Θ(θ)分別為

(55)

在求解自由振動特性時，不妨以振型對稱軸作為r軸，則A2=0，可得

Θ(θ)=A1cosnθ

(56)

將式(56)代入式(53)可知R(r)需要滿足微分方程：

r2R″+rR′-(μr2+n2)R=0

(57)

針對μ的取值，對以下幾種情況進行分類討論：

1)μ<0，方程(52)的通解為

(58)

此時方程(57)為n階貝塞爾方程，通解為

(59)

φ(r,θ,x)=Jn(βnsr)cosnθ[Enssinh(βnsx)+

Fnscosh(βnsx)]

(60)

式中：βns>0。

2)μ>0，方程(57)為n階虛宗量貝塞爾方程，通解為

(61)

由R(0)為有限值知D2=0，同時考慮到柱面剛性壁面條件R′(a)=0得D1=0。因此在μ>0時，φ(r,θ,x)不存在非零解。

3)μ=0，方程(52)的通解為

X(x)=E1x+E2

(62)

此時方程(57)為歐拉型常微分方程，其通解為

(63)

由R(0)為有限值知F2=G2=0，同時考慮到R′(a)=0可得F1=0。因此式μ=0時，速度勢函數通解為

φ(r,θ,x)=cosnθ(anx+bn)δn0

(64)

綜上可知，對于確定的n，速度勢函數的一般解為

φ(r,θ,x)=cosnθ{(anx+bn)δn0+

(65)