基于電子隧道效應的納米梁非線性振動控制

姜瑞瑞， 劉燦昌， 李 磊， 秦志昌， 萬 磊， 孔維旭， 周長城

(山東理工大學 交通與車輛工程學院， 山東 淄博 255049)

隨著微納米技術的快速發展，納機電系統(Nano-Electromechanical Systems，NEMS)的振動控制成為研究熱點問題之一。納米梁具有高固有頻率、高承載能力、高靈敏度和低功耗等特點，常用來制作高頻諧振器。但是，隨著納米梁尺寸的進一步減小，在大振幅振動中容易出現多值、分岔等非線性現象，導致諧振器出現不穩定振動，甚至產生吸合現象，影響NEMS器件的工作穩定性。因而，納米梁的非線性振動控制成為微機電系統的一個重要研究方向。由于NEMS器件處于納米尺寸，常用的振動信號傳感器尺寸接近甚至大于控制器件的尺寸，難以應用于納米梁振動控制，振動信號傳感成為納米梁振動控制的一個難題。

隨著傳感器技術的迅速發展，基于隧道效應的信號傳感研究正逐步引起科研工作者的注意。Rockstad等[1]利用電子隧道效應原理制作了檢測小位移的高性能加速度傳感器。李夢超等[2-3]對基于隧道效應的納米振動傳感器的理論、技術及實現方法進行了初步的研究和探索，并進行了振動檢測試驗，得出基于隧道效應的測振傳感器具有很高的靈敏度、良好的頻率特性。夏一等[4]對隧道傳感系統微位移機構的主從關聯優化進行了研究，建立了物理模型并進行了優化計算和分析。陳帆等[5]基于隧道效應的原理搭建了閉環控制系統，利用仿真現象和實驗結果進行控制特性和動態響應的分析。Opacak等[6-7]研究了電子在復勢壘中的隧穿現象，并給出了共振頻率表達式。

近年來，對于納機電系統的非線性振動分析與控制研究取得較大的進展。張文明等[8-9]研究了參數激勵作用下梁式微結構共振傳感器的非線性響應。宋震煜等[10]利用連續體彈性理論建立了物理模型，并分析了納米梁的幅頻特性和納米梁非線性產生的物理機制。Zhao等[11]研究了納米梁的非線性自由振動，得到了非線性方程的近似解析解。Liu等[12]采用時滯反饋控制方法，研究得到了納米梁諧波激勵主共振的最優控制。Gong等[13]應用多尺度法求得系統超諧共振的幅頻響應方程，分析了振動方程解的穩定性。Dumitru等[14]研究了靜電驅動懸臂梁微諧振器的非線性響應。Rhoads等[15]通過提出一種新型的納米梁結構裝置，研究了受交流激勵電壓幅值控制的響應特性。Shaat等[16]研究了納米材料的靜電驅動梁梁結構和尺寸大小對靜電驅動納米梁固有頻率、非線性動力學的影響。Najar等[17]在考慮了小尺度效應下，研究了在非線性力和直流電壓作用下納米梁的動態響應。Bornassi等[18]利用Euler-Bernoulli梁建立了納米器件在靜電力和分子間力作用下的運動方程，利用微分求積法求解非線性動力學方程。

利用時滯反饋對非線性振動進行控制成為非線性系統振動的重要研究方向。張舒等[19]介紹了時滯耦合系統中新的定量分析方法、具有耦合時滯的非線性系統中耦合時滯和非線性參數的辨識方法與實驗實現等問題的研究進展。Sun等[20]提出了一種具有時滯耦合主動控制的非線性組合結構并建立了數學模型，對不同的結構參數和時間延遲進行了穩定性分析。Liu等[21]提出了一種優化的延遲反饋控制方法，以非線性振動穩定條件和最優時滯為約束條件，利用最優化方法計算獲得最佳反饋控制參數。孫清等[22]采用增量諧波平衡法求得了含雙時滯振動主動控制系統的周期解，得到當時滯量和反饋控制增益匹配適當時，可以使系統保持穩定狀態。

本文研究了基于隧道效應信號提取的納米梁非線性振動控制，將隧道效應理論應用于納米梁非線性振動的信號提取中，提高了信號提取的靈敏性與精確性。以Euler-Bernoulli梁作為振動的物理模型，考慮時滯的影響，對靜電激勵下的納米梁非線性振動控制進行了分析研究，得到基于隧道效應的納米梁非線性振動方程，利用多尺度法得到納米梁主共振的幅頻響應方程。研究了直流和交流激勵電壓、阻尼、控制參數、時滯等與納米梁振動穩定性和振幅之間的關系，分析了減弱系統非線性、增強系統穩定性的影響因素。

1 隧道效應傳感原理

電子隧道效應是能量低于所面對勢壘的電子貫穿通過該勢壘的量子效應，可以用于電流信號檢測，具有指數靈敏性[23]，如圖1所示。由隧道效應產生的作用于振動控制信號電壓為

(1)

式中:κ為比例系數；V為偏置電壓；β為轉換因子；φ是勢壘高度；d為納米梁與極板間的初始距離；w為納米梁振動時的撓度；R為控制電路中的采樣電阻。

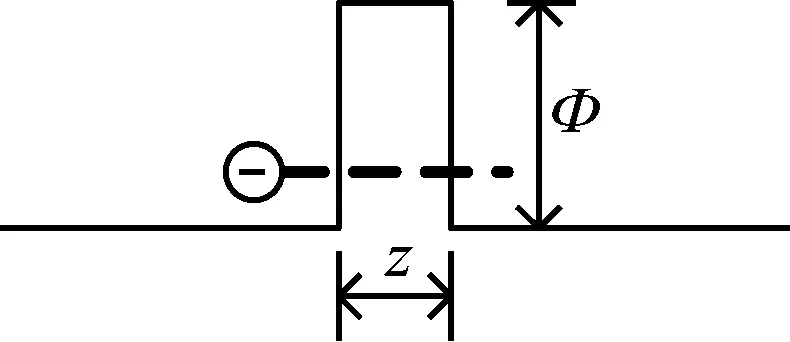
圖1 電子隧道效應現象示意圖Fig.1 Schematic diagram of electron tunneling effect

2 基于隧道效應納米梁靜電激勵振動控制模型

以一端固定、一端自由的懸臂納米梁為動力學模型，如圖2所示。AB和CD為兩個控制極板，分別對位移和速度進行控制，EF為靜電驅動極板，其中，控制極板或驅動極板邊界點A、B、C、D、E、F分別對應的參數坐標值為x1、x2、x3、x4、x5、x6，xi為點到懸臂梁固定端的坐標值，納米梁與極板間的初始距離為d。在納米梁左側底部有一探測針，采集納米梁振動信號。

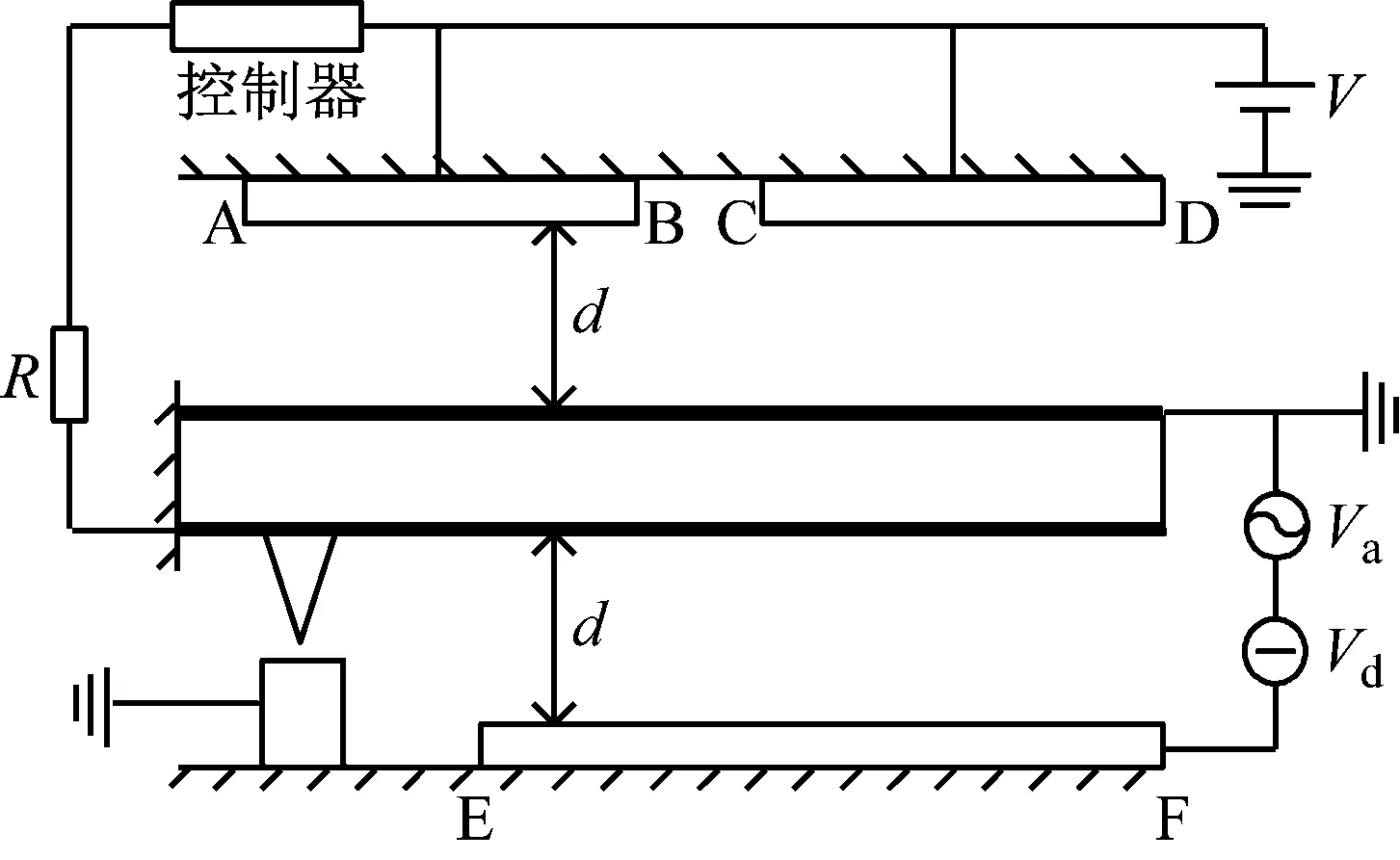
圖2 納米梁振動模型Fig.2 Vibration model of nanobeam

作用于納米梁與靜電驅動極板間的控制電壓為

Ucd=Vc+Vckw(xi,t)

(2)

(3)

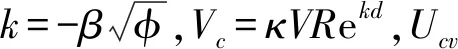
考慮時滯控制，則作用于納米梁與靜電控制極板間的控制電壓的平方可用以下公式表示

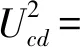
(4)

(5)

式中：g1為控制參數。

靜電控制力可表示為

(6)

式中：ε0是真空介電常數；W是納米梁的寬度；Hij=[H(x-xi)-H(x-xj)],H(x-xi)為階躍函數。

作用于納米梁與靜電驅動極板間的靜電驅動力可表示為

(7)

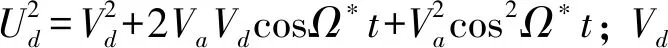
在靜電控制力作用下，基于隧道效應的納米梁非線性振動微分方程可表示為

(8)

式中：()(4)=?4/?x4，(·)=?/?t，(··)=?2/?t2。E，I，ρ分別表示楊氏模量、截面慣性矩和納米梁密度，c*是阻尼系數。

引入無量綱量

(9)

式中：l表示納米梁的長度。將式(4)～(7)和(9)代入式(8)中，考慮時滯作用，得到在控制力作用下基于隧道效應的納米梁無量綱非線性振動微分方程為

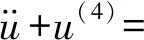
(10)

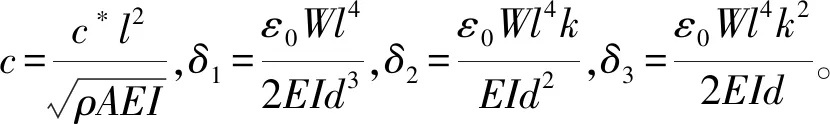
對式(10)中的1/(1-u)2、1/(1+u)2進行泰勒級數展開，本文不考慮激勵電壓兩階諧波對納米梁振動的影響，假設振動系統是弱非線性系統，用小變量ε表示系統參數，得到納米梁非線性彎曲振動方程為

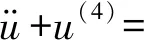
2εδ1(1+2u+3u2+4u3)H56VaVdcosΩt-

εδ1(1-2u(t-τ)+3u2(t-τ)-

(11)

3 基于隧道效應的納米梁非線性振動控制

應用多尺度法將方程(11)的近似解用以下形式進行表示[24]

u(x,t,ε)=u0(x,T0,T1)+εu1(x,T0,T1)+…

(12)

式中：ε是無量綱參數；T0=t表示快變時間尺度；T1=εt表示慢變時間尺度。

將式(12)與其對時間的導數代入式(11)，令公式左右兩邊ε同次冪的系數相等，得到一組線性偏微分方程，即

(13)

(14)

考慮納米梁主共振的情況，取外激勵頻率近似等于固有頻率，則激勵頻率為

Ω*=ωk+εσ

(15)

式中：σ是激勵頻率調諧參數。

在時滯作用下，將式(13)的近似解表示成如下形式

(16)

(17)

將式(16)、(17)代入式(14)，經模態正交化處理后，為避免出現久期項，要求函數A應滿足

(18)

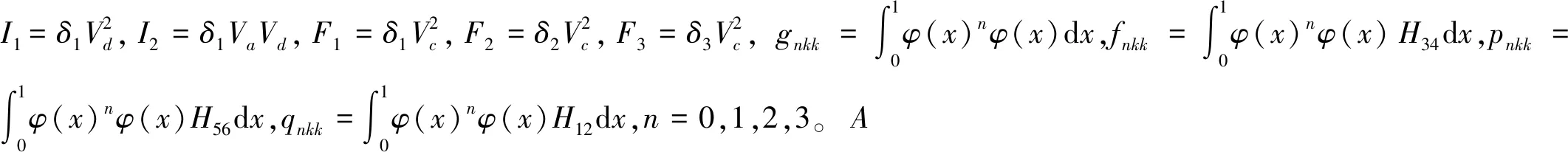
(19)

將復函數(19)及其共軛函數代入式(18)，分離方程的實部與虛部，得到在時滯作用下，一次近似解的振幅ak和相位角γk滿足的一階常微分方程為

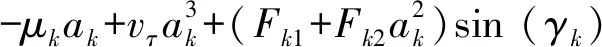
(20)

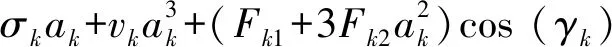
(21)

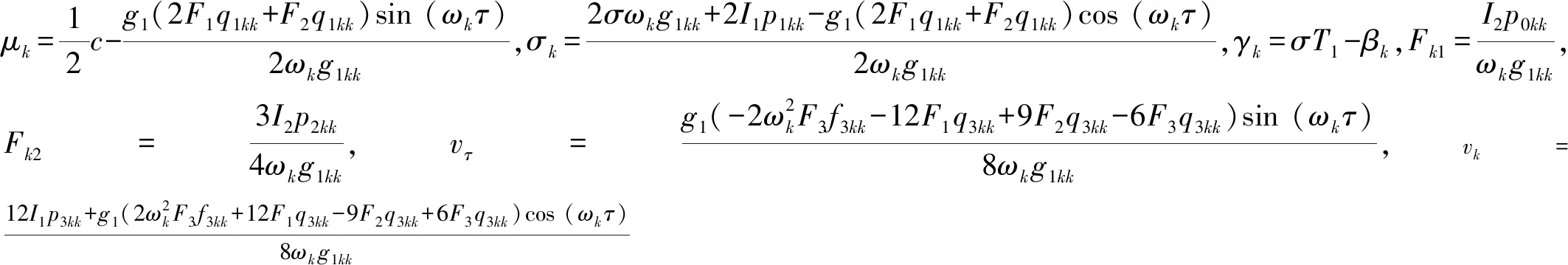
為確定納米梁穩態振動時對應的振幅ak和相位γk，令D1ak=D1γk=0，得到振幅和相位滿足的代數方程為

(22)

(23)

求得系統主共振的幅頻響應方程和相頻響應方程為

(24)

(25)

分析式(24)得，幅頻響應方程振幅值與調諧參數、控制參數、時滯參數、激勵電壓和納米梁參數等有關。

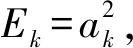
(26)

式(26)對σ求導，令?Ek/?σ=0，在共振頻率點處下式成立

vkEk+σk=0

(27)

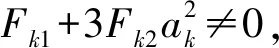
(28)

求得主共振的最大振幅akmax的兩個解為

(29)

分析式(29)可得，主共振的峰值大小與非線性因素無關。

4 數值模擬及分析

本文以Euler Bernoulli梁一階振動模態為例進行分析[13]，納米梁的參數值如表1所示，仿真得到系統非線性振動分析與控制的幅頻響應曲線圖。

圖3是振動阻尼項隨時滯和反饋控制增益變化曲線。由圖可知，當反饋控制增益一定時，阻尼項隨時滯參數呈周期性變化；當時滯參數一定時，反饋控制增益也能改變阻尼項的數值。由此可得，通過改變反饋控制增益和時滯可以改變振動阻尼項數值，擴大了振動控制的控制參數取值范圍。

表1 納米梁參數值Tab.1 Parameters of nanobeam

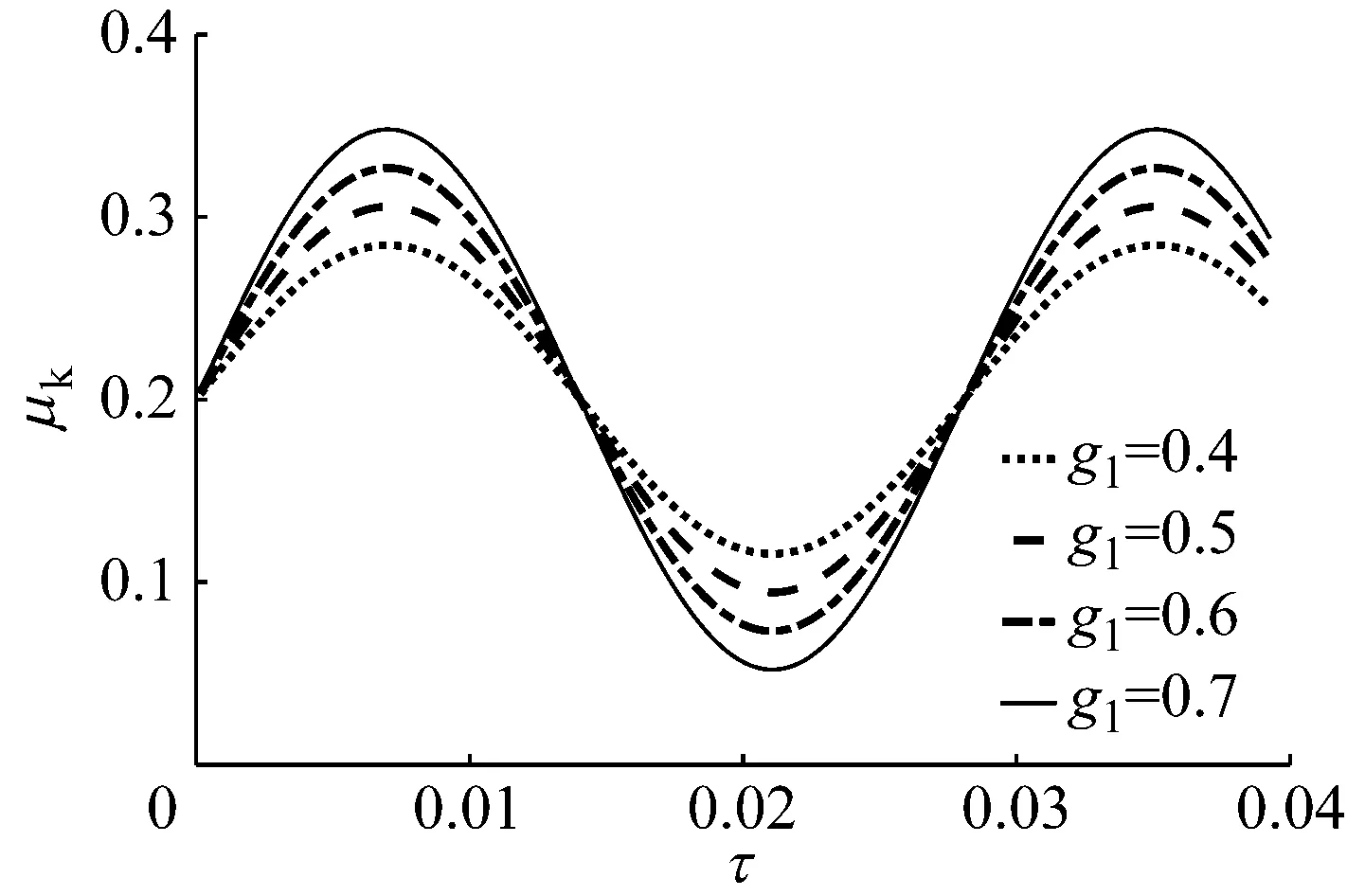
圖3 控制參數不同時，振動阻尼項隨時滯參數變化曲線

Fig.3 Curves of the vibration damping term varying with time-delay parameters for different control parameters

圖4是時滯參數不同時，振動阻尼項隨控制參數變化曲線。分析圖4得，在所選取范圍內，當控制參數保持一定時，時滯參數與振動阻尼項之間呈線性變化，隨著控制參數的增加，振動阻尼項隨之增大，保持控制參數不變，振動阻尼項幅值大小隨時滯參數的增加而增大，這與圖3所得結論相一致。

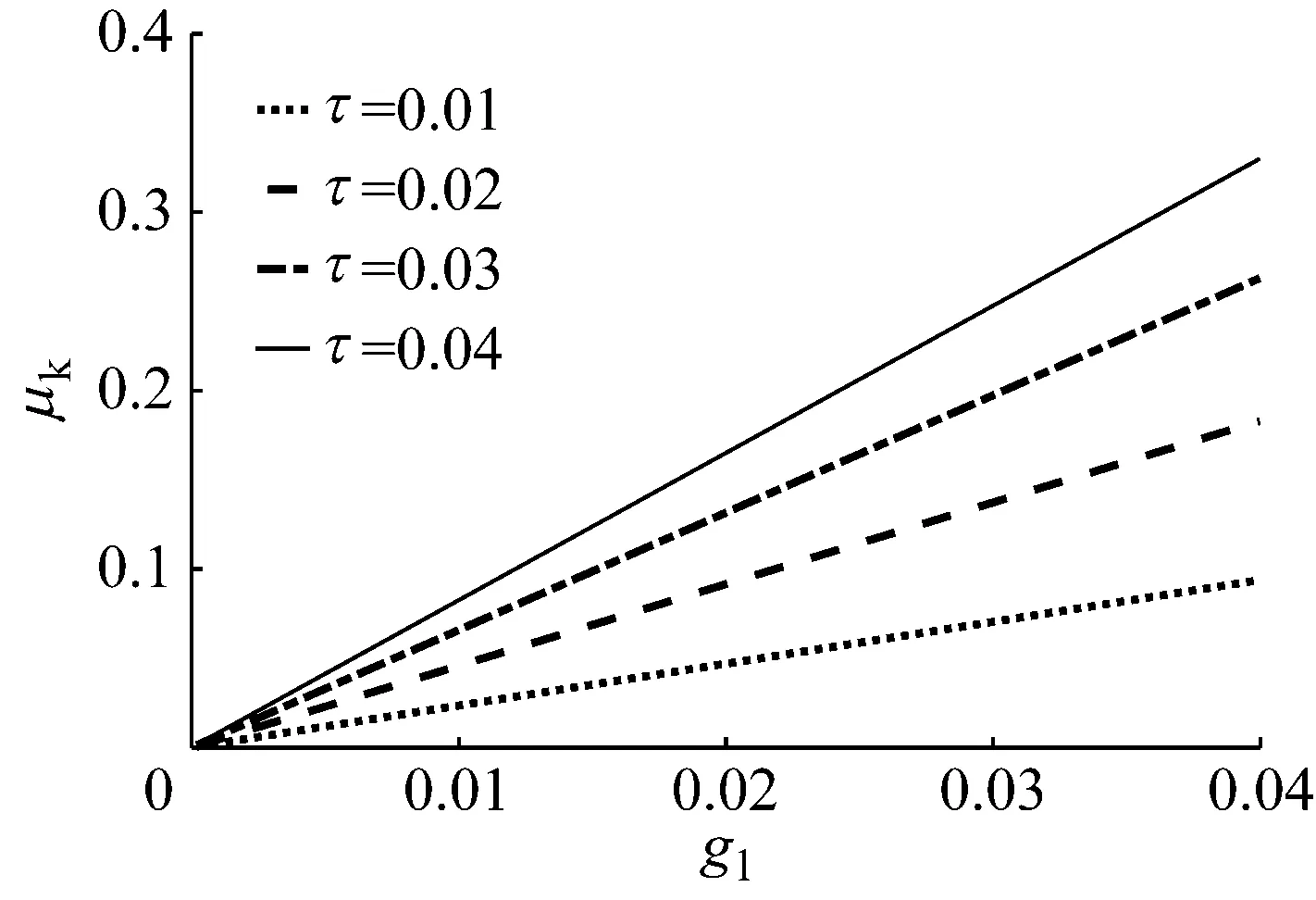
圖4 時滯參數不同時，振動阻尼項隨控制參數變化曲線Fig.4 Curves of the vibration damping term varying with control parameters for different time-delay parameters

圖5是系統振動控制參數不同時的幅頻響應曲線。分析圖5可得，在時滯參數保持不變的情況下，改變系統的控制參數對振幅的大小產生一定的影響，隨著控制參數的增大，系統的振幅逐漸減小。當控制參數g1的取值為0時，在共振頻率點的左側，振幅隨著頻率的增大而增大，在共振頻率點的右側，出現非線性區間，系統振動不穩定。當控制參數g1為0.6時，振幅峰值減小至0.30，振幅峰值點偏離共振頻率點的距離減小。當控制參數g1的數值由0增加到0.6時，系統的最大振幅逐漸減小，系統振動由不穩定狀態趨于穩定狀態。隨著控制參數幅值的增加，系統的振幅峰值點偏離共振頻率點的距離逐漸減小，系統的振動逐漸趨于穩定狀態。由此可得，增大系統振動時的控制參數可以減弱系統振動的非線性。

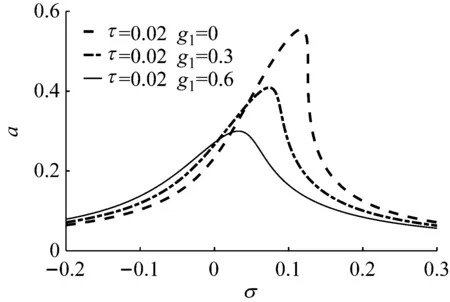
圖5 控制參數不同時的幅頻響應曲線Fig.5 Amplitude-frequency curves with different control parameters

圖6是系統時滯參數不同時的幅頻響應曲線。分析圖6可得，在系統振動控制參數保持一定時，改變時滯反饋參數可以改變系統振幅的大小，振幅幅值隨時滯反饋參數的增大而減小。當時滯反饋參數τ為0時，振幅峰值點向右偏離共振頻率點，系統表現為非線性振動，當時滯增益參數τ由0增加到0.02時，系統的振幅峰值點向右偏離共振頻率點的距離逐漸減小，系統振動的非線性明顯減弱，逐漸趨于穩定狀態。由此可得，選擇合適的時滯參數可以明顯降低系統振動的非線性。

圖7是控制參數不同時，最大振幅隨時滯參數變化曲線。由圖7分析得，當時滯參數保持不變時，隨著控制參數的增加，系統的最大振幅akmax隨之減小，當控制參數保持一定時，最大振幅akmax隨時滯參數的改變呈周期性變化，這與公式(29)所得結論一致。

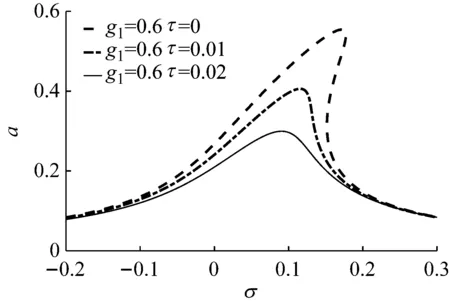
圖6 時滯參數不同時的幅頻響應曲線Fig.6 Amplitude-frequency curves with different time-delay parameters

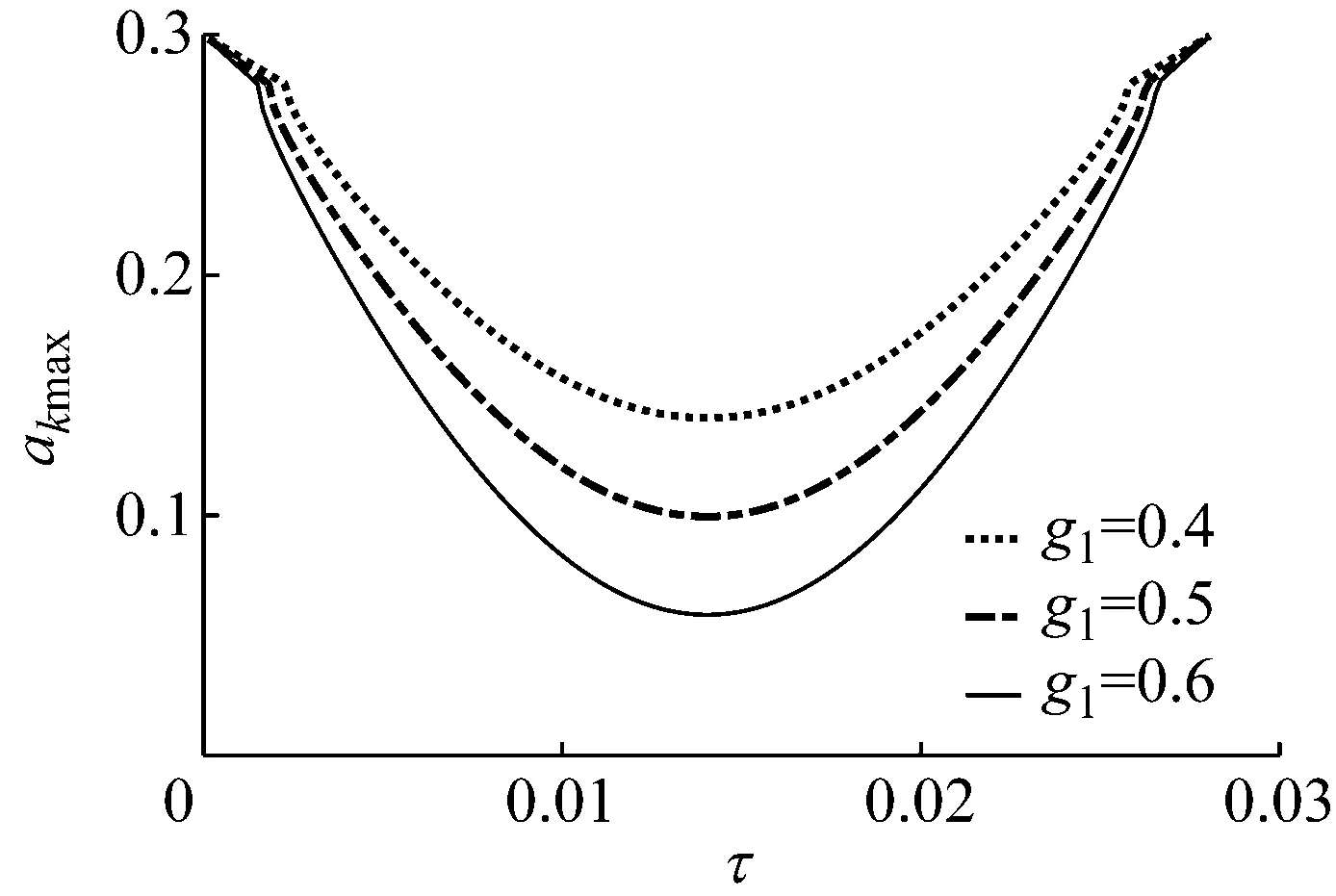
圖7 控制參數不同時，最大振幅隨時滯參數變化曲線Fig.7 Curves of the peak amplitude varying with time-delay parameters for different control parameters

圖8是時滯參數不同時，最大振幅隨控制參數變化曲線。分析圖8得，當時滯參數一定時，最大振幅akmax隨控制參數的增加而線性減小，當保持控制參數不變時，時滯參數越大，最大振幅akmax越小，這與公式(29)結論一致，也與圖7所得結論相對應。

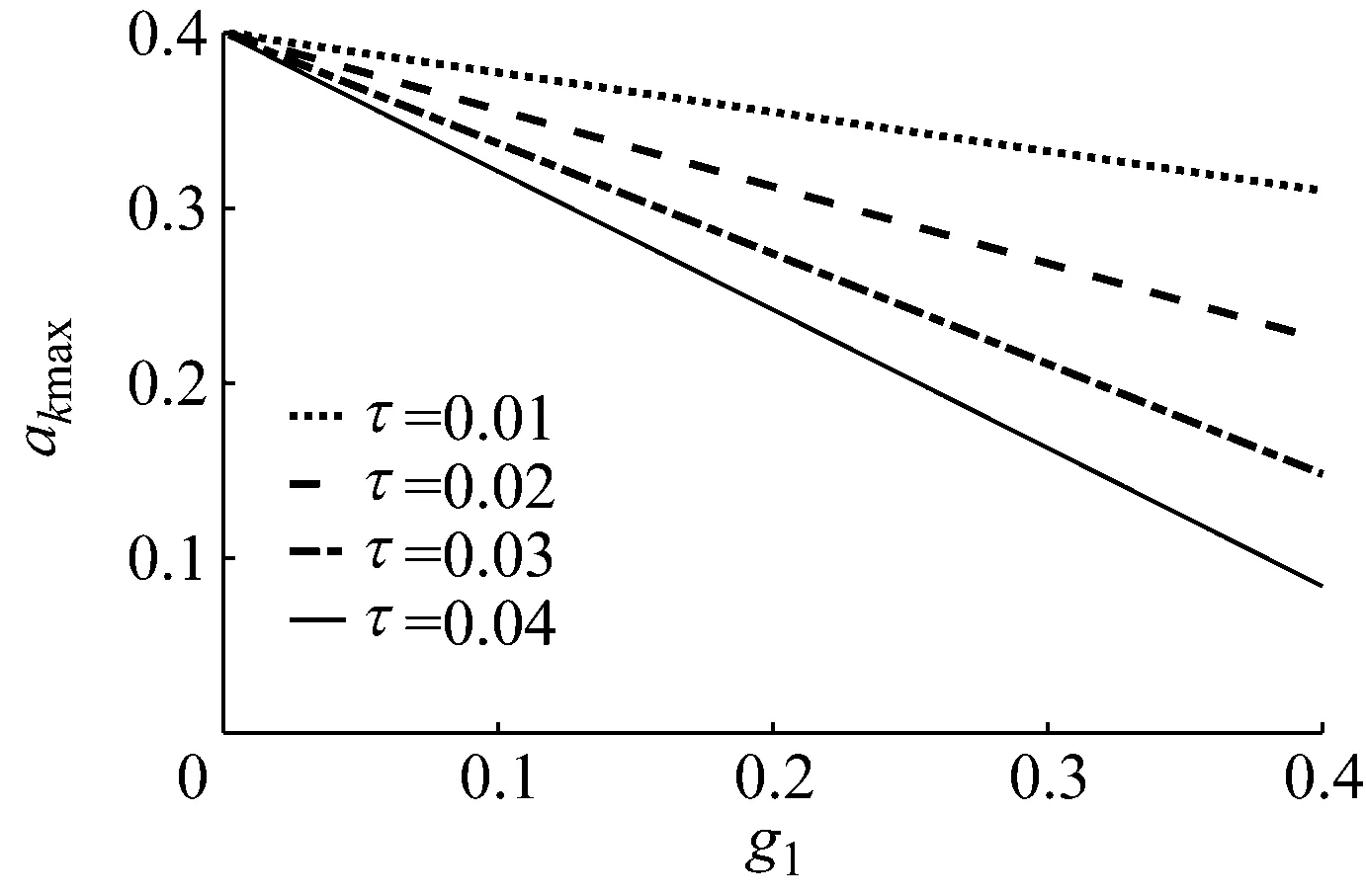
圖8 時滯參數不同時，最大振幅隨控制參數變化曲線Fig.8 Curves of the peak amplitude varying with control parameters for different time-delay parameters

圖9是時滯參數不同時，非線性項隨納米梁長度變化曲線。非線性項是決定系統振動是否穩定的主要因素，將非線性項控制在合理的范圍內有助于保證系統振動的穩定性。分析圖9可得，當時滯參數一定時，非線性項νk隨納米梁長度的增加而減小，當納米梁的長度保持一定時，時滯參數越大，非線性項νk隨之增大。由此可得，通過改變納米梁的時滯參數可以使系統振動的非線性項控制在合理范圍內，從而增加系統的穩定性。

圖9 時滯參數不同時，非線性項隨納米梁長度變化曲線Fig.9 Curves of the nonlinear term varying with nanobeam length for different time-delay parameters

圖10是時滯參數不同時，時滯非線性項隨納米梁長度變化曲線。由圖10可得，當時滯反饋參數一定時，時滯非線性項隨納米梁長度的增加而增大，當納米梁的長度一定時，時滯非線性項ντ隨時滯反饋參數的增大而增大。由此可得，選取合適的時滯參數可以實現對納米梁非線性振動的控制。

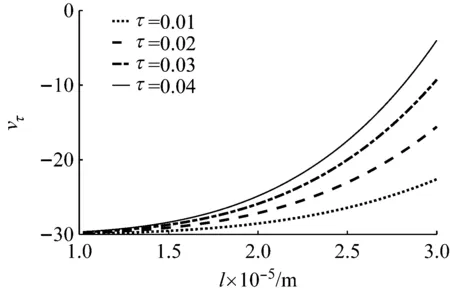
圖10 時滯參數不同時，時滯非線性項隨納米梁長度變化曲線Fig.10 Curves of the time-delay nonlinear term varying with nanobeam length for different time-delay parameters

圖11和圖12分別是直流激勵電壓幅值和交流激勵電壓幅值不同時的幅頻響應曲線。由圖可知，隨著直流或交流電壓幅值的減小，系統振動的振幅峰值隨之減小，系統的非線性減弱。當直流或交流激勵電壓幅值相對較大時，振幅隨頻率的變化呈非線性變化趨勢，振動不穩定；當直流或交流電壓幅值逐漸減小時，系統非線性減弱。當振動頻率一定時，隨著直流或交流激勵電壓幅值的減小，系統的振動幅度逐漸減小，衰減幅度分別為52%和48%，振幅峰值點處頻率逐漸趨于共振頻率，且系統振動由非線性振動趨于線性振動。由此可得，降低直流或交流激勵電壓幅值可以減弱甚至消除系統的非線性。

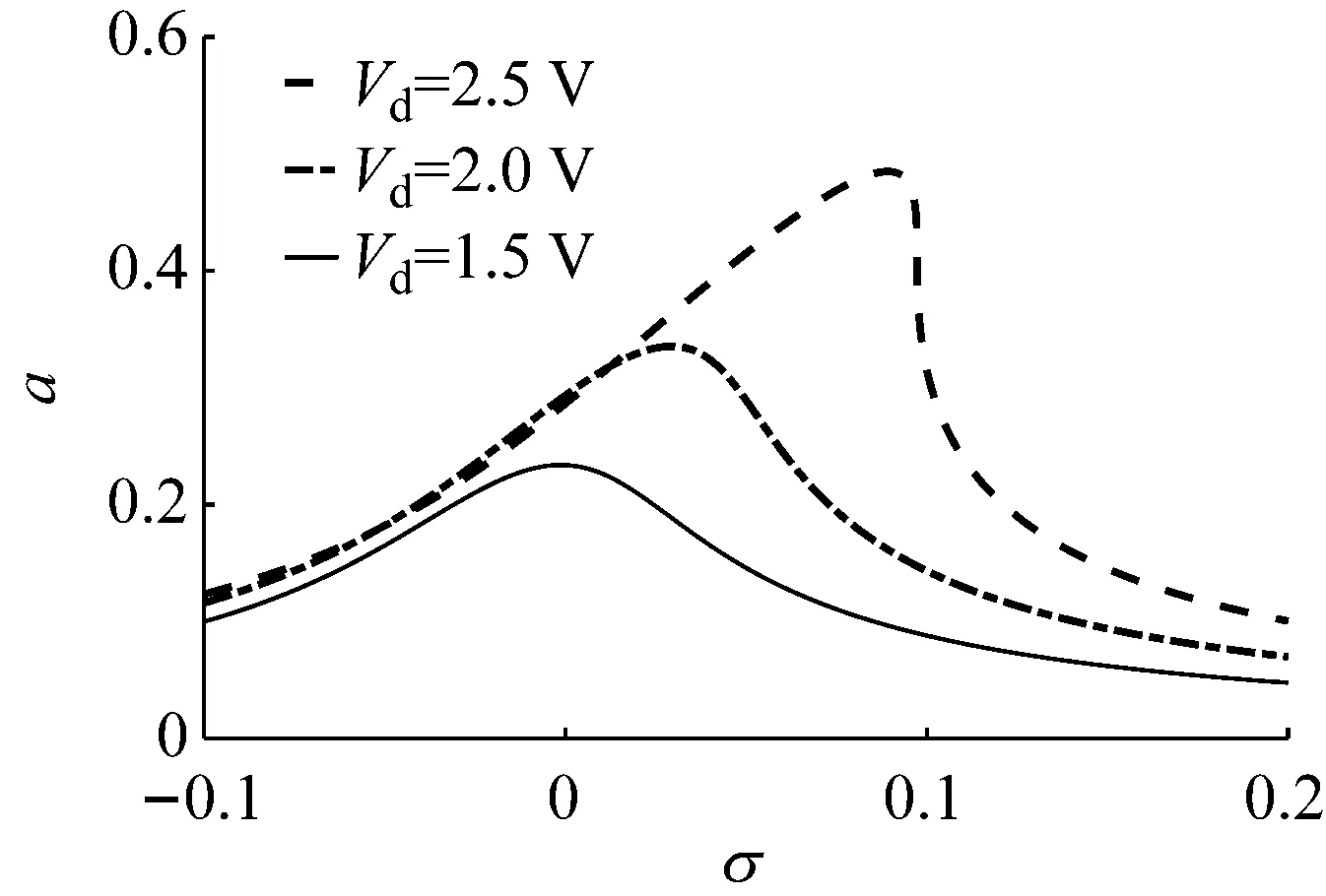
圖11 直流激勵電壓幅值不同時的幅頻響應曲線Fig.11 Amplitude-frequency curves for different amplitude of direct current excitation voltage

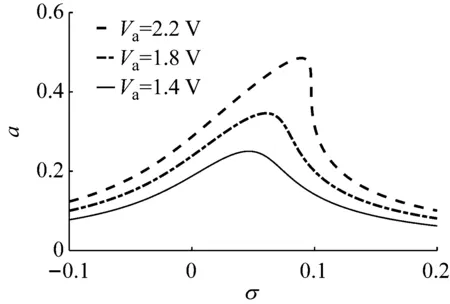
圖12 交流激勵電壓幅值不同時的幅頻響應曲線Fig.12 Amplitude-frequency curves for different amplitude of alternating current excitation voltage

為了證明本文理論分析的正確性，對本文多尺度近似解析方法和數值方法的計算結果進行對比分析。數值方法(Long Time Integration，LTI)計算結果在圖中表示為不連續的離散點，多尺度方法(Method of Multiple Scales，MMS)計算結果用實線表示。時滯參數分別取τ=0和τ=0.02。由圖13可知，理論分析結果與數值計算結果符合較好，兩種計算結果的一致性表明本文的理論公式分析方法具有一定的合理性。

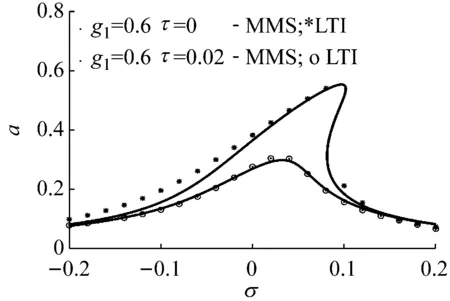
圖13 多尺度方法與數值運算結果比較Fig.13 Comparison of calculation results between the method of multiple scales and the numerical integration

5 結 論

(1) 直流和交流激勵電壓幅值、系統振動時的控制參數都是影響系統振幅的因素，改變其中任何一個參數均對系統振動時的振幅產生較大的影響。通過適當減小直流或交流激勵電壓幅值、選擇適當的控制參數可以減小系統的振動幅值。

(2) 選取合適的控制參數和時滯參數可以減小系統振動時的振幅，同時對振動阻尼項產生一定的影響，可以有效的對系統振動時的非線性進行控制與調節，提高系統的穩定性。

(3) 分析幅頻響應曲線可得，當納米梁各參數值保持一定時，通過適當減小直流或交流激勵電壓幅值、選取合適的時滯參數和控制增益可以減弱系統振動的非線性。