打磨課堂，追尋數學教學本質
——兩次教學《小數加減法》的體會與思考

林 君

一、解讀教材——錯估了學情

《小數加減法》是人教版四年級下冊第六單元的教學內容，該內容是在學生已經掌握了整數加減法的豎式計算方法、一位小數的加減法、整數的四則運算、整數加法的運算定律和減法的性質及其簡便運算、小數的意義和性質等知識的基礎上進行教學的，又是今后學習小數加減混合運算、小數乘除法豎式計算、小數四則混合運算等知識的重要基礎。

本節課的教學重點是掌握小數加減法的計算方法，難點是理解相同計數單位才能直接相加減的算理。教材對此也做了精心編排，教材分兩個例題逐層展開對算理的探究：例1以本單元主題圖的買書情境為線索展開教學，以圖文結合的形式給出了小麗所買的兩本書的價格，并分別提出了用加法和減法解決的數學問題，自然地引入小數加、減法的學習，雖以解決問題的方式呈現，但這里重點不是解決問題，而是如何計算小數加減法，教材通過簡單的提示語，突出了豎式計算小數點對齊的重要性。例2教學數位不同的小數加、減法豎式計算，從小數加法到小數減法，由數位相同到數位不同，教材在編排上既體現了由淺入深、由易到難的特點，又有目的地分散了小數加、減法筆算的難點，符合學生的認知規律，小數減法是教學的難點，因而教材通過小精靈的提問來促進學生思考，突出小數點對齊的必要性。但我有個疑惑：究竟是僅以例1為一例進行教學，還是例1與例2兩個例題一起教學，因為在我備課的過程中也去了解了其他教師同樣上《小數加減法》一課的案例，發現有的是僅教學例1，也有的是兩個例題一起教學，最后自己斟酌后選擇保守的僅教學例1，想著把數位相同的小數加、減法的重難點教透了，便于例2的自然而然地順學。

欣欣然付諸實踐，但實際的課堂教學卻讓我出乎意料。

二、實踐課堂——然“裹足前行”

1.觀察發現，提出問題。

師：從圖中你獲得了哪些信息？這里是兩本書的價錢，誰來讀一讀？根據你們讀到的信息，能提出什么數學問題呢？

2.遷移經驗，探究小數加法算法。

師：根據你們提出的這兩個問題，該怎么列式？（6.45+4.29和6.45-4.29）

師：先來看6.45+4.29，大家先估算一下，買這兩本書一共花了多少錢？

師：這是兩位小數的加法，用豎式該怎樣計算呢？根據你的經驗，想一想，當我們遇到新知識時通常會怎么做？四人小組合作探究6.45+4.29的豎式計算方法。

3.交流匯報，說清算理。

師：老師挑選了幾個具有代表性的作品，看一看，你的方法跟哪個一樣？這些方法都正確嗎？說說你的想法。

預設：我認為①是正確的。和整數加減法一樣，一位對著一位加。

師：一位對著一位是什么意思？怎樣就一位對著一位了呢？有什么方法能快速將相同數位對齊？（小數加法中，只要小數點對齊，才能做到相同數位對齊）

疑惑：為什么一定要相同數位對齊？末位對齊不可以嗎？

（百分位的計數單位是0.01，十分位的計數單位是0.1）

預設：我認為②是正確的。先把6.45元和4.29元換算成以“分”為單位的整數，根據整數加法的筆算方法算出和是1074，再把1074分換算成10.74元。

預設：我認為③、④是錯誤的。對于③，百分位上的數相加滿十，卻沒有向十分位進1；對于④，結果忘記點上小數點了。

4.討論比較，優化算法。

師：比較①和②兩種方法，它們有什么區別和聯系？你更喜歡哪種方法？為什么？

5.練習一。

師：大家討論一下，在計算12.53+4.67時，得數末尾是“0”，這個“0”該怎么辦？6.07+4.89這道算式，整數部分相加后是10，整數部分個位上也是“0”，這個“0”可以省略嗎？

小結：小數加法計算結果的小數部分末尾出現了0，我們要對結果進行化簡，在橫式上寫答案時就寫最簡結果，這就是數學上簡潔美的體現。

6.自主遷移，探究小數減法的算法。

師：看來小數加法同學們都會算了，那6.45-4.29這道小數減法，你們會計算嗎？試一試。

師：聽了他們的介紹后，你有什么想說的嗎？在計算小數減法時，你有什么要提醒大家注意的？

預設：小數點要對齊；從末位算起，哪一位不夠減要從前一位退一，最后的得數別忘了添上小數點；計算結果的小數部分末尾出現了0，一般要去掉。

7.引導比較，深化算理。

師：回顧剛才我們研究小數加減法的過程，誰來說說我們是怎樣解決問題的？

師：是的，我們將小數加法轉化為整數加法，并借助整數加法計算的經驗來探究小數加法的計算方法，然后借助小數加法與整數減法的經驗來探究小數減法的計算方法。看來，小數加減法和整數加減法之間有著密切的聯系，它們的計算方法都是要相同數位對齊，而內在的大道理都是計數單位相同。對于小數加減法，要想相同數位對齊，只要小數點對齊即可。

40分鐘的一節課，僅用20分鐘就將例1的內容全部完整消化，學生間的交流反饋是如此的精準，幾乎不需要教師的提示就能解釋為什么，且能在教師的追問下將本節課的教學難點分析透徹，接下來的時間就開始了漫長的練習環節。是的，這節課的教學目標我設定的太有問題了，自己沒有很好地前測了解學生已有的生活經驗和知識基礎，就想當然地設定了教學目標，對于這節課的例1，學生能根據三年級下學期一位小數的加減法知識，很好地順利完成。

三、問題剖析——方深悟“規律”

上述課堂實踐無疑暴露了兩個問題：一是對學生的認知起點把握失當，過低估計了學生；二是沒能更好地解讀教材，對例1與例2之間的前后聯系沒有把握到位。對于這單元的例1，學生能根據一位小數加減法的知識，很好地完成，而對于例2，學生同樣能借助例1所學的新知及整數加減法的知識，很好地理解并掌握，那么當學生已經都會了，教師沒東西可教的時候，接下去怎么教？相信熟悉教材后，會發現兩個例題的教學重點應是例2的添“0”，應該刻意留一題讓學生思考：出現新問題，與原問題相比，新問題的問題在哪？（小數位數不同）怎么解決？即使最后學生呈現的結果一直都對，也沒關系，至少在計算的過程中也存在著差異，也可以讓學生詳細地來說一說，如，當一名學生說道添“0”，教師可以問：他寫“0”了，對嗎？可以嗎？為什么題目中沒寫“0”，你卻要寫“0”？在多次的追問下，讓學生明白，數位對齊，才不容易出錯。

四、再次實踐——知“順木之天”

依據上述的思路，我重新設計教學，再次在實踐中檢驗。

1.別有用心的課前談話。

師：同學們，你們知道有哪些節日嗎？其實，在我們生活中有很多有意義的日子。你們知道世界讀書日嗎？這是去年讀書日的時候在寧波開展的一些活動，咱們學校有沒有開展過類似的活動呢？你能給今天來的老師們做一下介紹嗎？

2.獨具匠心的情境引入。

師：世界讀書日馬上就到了，老師班里的同學都在挑選圖書，現在有這樣四種書，想要買兩種，你打算怎樣買？

預設：我想買《笑貓日記》和《馬小跳》。

追問：一共要多少錢呢？算式怎么列？（9.42+10.47）

學生表達不同的買書情況。（將所有的可能都羅列出來）

師：要求兩本書一共要多少錢，可以用加法進行計算。觀察一下這些算式，有什么特點呢？

3.洋溢真我的新知探究。

（1）探究小數加法。

①嘗試計算。

師：如果我想要買這樣兩本（《笑貓日記》和《馬小跳》），你能算出一共要花多少錢嗎？如果是這兩本書（《笑貓日記》和《西游記》）又要花多少錢呢？你會算嗎？請你用豎式計算。

②理解算理。

師：9.42+10.47的得數是19.89，對嗎？再來看他的豎式，他是怎樣算的呢？誰看明白了？

預設1：小數點對齊。

預設 2：2+7=9，4+4=8……

預設3：相同數位上的數相加。

師：（9.42+11.7） 那這一題呢？誰再來介紹一下。這里的4為什么和7相加而不和2相加呢？

預設1∶4表示4角，7表示7角，2表示2分，角和角相加。

預設2∶4在十分位上，表示4個十分之一……

師：通過計算這兩道題目，你認為小數加法應該怎么計算呢？有什么好的辦法能幫助我們快速地做到相同數位對齊？

（2）探究小數減法。

師：同學們，通過計算兩本書一共要多少錢，我們知道了計算小數加法要先把小數點對齊，再把相同數位上的數相加。現在老師帶來了50元錢，想買這兩本書（《笑貓日記》和《馬小跳》），能找回多少錢呢？

（3）探究算理算法。

師：算式對嗎？得數正不正確？你是怎么想的？我們看他的豎式，對不對？他是怎么想的和怎么算的呢？

預設：把50看成50.00。

追問：為什么要添上兩個0呢？

預設：小數部分沒有，所以要添上兩個0。

師：誰也是這樣想的？原來你們看到整數減小數，整數的小數部分沒寫出來，所以在整數后面點上小數點，添上0，再相減。那50為什么要寫在這里呢？

（4）小結。

師：剛才我們一起走進世界讀書日，通過購買圖書解決了小數加法和小數減法的問題，你有什么收獲呢？

小結：通過剛才的學習，我們知道了在計算小數加減法的時候，先把小數點對齊，也就是相同數位上的數對齊，再將相同數位上的數相加、減。

4.激蕩思維的課堂練習。

（1）筆算。（從以下題目中選擇四題筆算，并任選其中一題進行驗算）

①12.53+4.47＝

②0.63+1.5＝

③12+3.56＝

④7.33-6.7＝

⑤15.3-2.24＝

⑥10-5.6＝

得出：數學講究簡約之美，豎式中得數小數末尾的0可以省略不寫，橫式得數只要寫17就可以了。

（2）改錯。

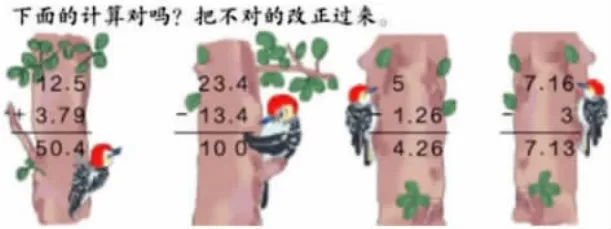
（3）解決問題。

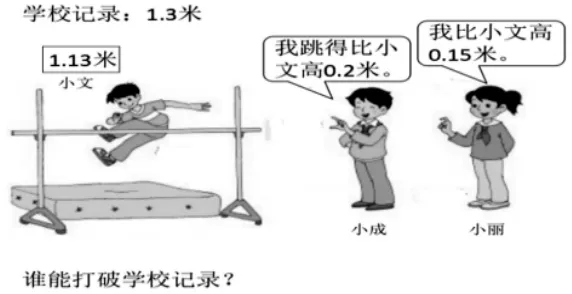
5.清新自然的課堂小結。

師：今天這節課我們一起再次研究了小數的加法和減法，你有什么新的收獲嗎？

五、課后感悟——覓“教學規律”

“順木之天，以致其性焉爾”出自柳宗元的《種樹郭橐駝傳》，說的是要想讓樹木活得長久，長得茂盛，就必須注意樹木的自然屬性。教學更需要我們既知學生之性，亦應知知識之性，方能悟其神，終使學生順利成長，其關鍵要抓好以下兩點。

1.前測學情，順學生之性。

在第一次教學中，我想當然地以為學生不會順利地探索數位相同的小數加減法的算理，再加以練習鞏固理解后才能真正掌握，由此來完成教學例1的一整節課，低估了學情，以致課堂教學內容不夠。“要帶學生到哪里去，首先要知道學生在哪里。”背離了學生的需求，教學只會浮于學生認知起點之上或低于學生認知起點，使知識失去了生長之根基，學生求知的火花也只能黯然而逝。可見，前測學情是上好課的基礎，依據學情施教是教學的根本。所以，把握學生的認知起點，順應學生的發展規律，才能教得踏實、學得有效，知識之花才能最終得到綻放。

2.參悟教材，順知識之性。

深入參悟教材，明其精髓，是教學的根本。在此基礎上再“跳”出教材，靈活運用，使教材為我所用，此為“入乎其內，又出乎其外”。而“入乎其內”是根基所在，“出乎其外”是拓展提升。那么，如何“入乎其內”呢？分析知識間的前后聯系和地位作用是深入參悟教材的關鍵所在，但這關鍵的一步卻往往流于形式。我們知道，教材編寫的依據主要有二：一是學生的年齡特點與認知規律；二是關注知識的發展體系。教材依據學生的認知規律，知識脈絡的呈現層層遞進。因此，參悟教材要先明晰各知識點在整個小學數學教材中的地位，在各年段、各冊、各單元中是如何生根發芽的。上述教材從整體上把握了小數加減法在小學階段的前后聯系，再對例1與例2展開研究，從知識內在聯系上鉆研教材，方可“出乎其外”。

打磨課堂，在看似熟悉而又與眾不同的細節上，關注數學的本質，關注學生的數學素養，使課堂教學更高效。