基于規則的最短路徑查詢算法?

李忠飛,楊雅君,王 鑫

1(天津大學 智能與計算學部,天津 300354)

2(數字出版技術國家重點實驗室,北京 100871)

3(天津市認知計算與應用重點實驗室,天津 300354)

近年來,隨著信息技術和互聯網的飛速發展,圖數據作為一種重要的數據模型變得愈加重要.在很多領域,圖數據刻畫了不同實體之間的相互關系,例如社交網絡[1,2]、道路交通網[3]、生物信息網[4]、計算機網絡[5]和Web 網絡[6]等.

其中,最短路徑查詢是圖數據管理中的一類非常重要的研究問題.在社交網絡中,每個人都構成了圖中的一個頂點,人與人之間的聯系則形成了邊.社交網絡中的最短路徑是網絡頂點影響力評判的重要因素,小世界網絡中,直徑的計算一般也是通過計算最長最短路徑得到的[7];在Web網絡中,數據轉發時每個路由器使用路由協議和鏈路狀態信息來識別從自己到其他路由器的最短路徑,網絡拓撲通常隨時間而變化,因此,一個高效的最短路徑算法在路由計算中顯得尤為重要[8];在道路交通網中,經常需要計算兩個地點之間的最短路徑,有時因為一些特殊的需求還要計算最小的前k條最短路徑[9-11].

在實際應用中,用戶往往需要查詢帶有約束條件的最短路徑.例如,某游客去一座城市旅行,他計劃首先前往某餐館就餐,然后分別參觀景點A～景點C,最后返回酒店.特別地,該游客計劃在參觀景點B之前先參觀景點A.因此,如何設計一條滿足用戶約束且代價最小的觀光路徑成為一個重要的問題.在該例中,道路交通網被建模為一張圖G(V,E),則上述問題可形式化描述為:給定起點vs和終點ve,尋找一條從vs到ve的最短路徑,使得此路徑經過用戶指定點集Vs?V中的所有點,且某些點的訪問要滿足一定的先后順序.在本文中,該問題被稱為基于規則的最短路徑查詢問題.

目前,存在少量工作研究了最優路徑查詢問題optimal route queries(ORQ).ORQ將圖G中全部頂點劃分為多個不同的類別,用戶查詢時,給出起點vs和一個訪問順序圖GQ.這里,GQ是一個有向無環圖,GQ中的每個點都對應于G中的一個類別信息,GQ中每條有向邊(c,c′)表示G中類別c優先于類別c′訪問.查詢結果是一條以vs為起點且滿足GQ的最優路徑.例如,某游客計劃去餐館、酒吧和電影院,每個類別都有多個具體的地點可供選擇,而且游客希望在去酒吧之前要先去餐館吃飯,因此,他需要制定一條路線使得在滿足約束條件的前提下路線的總距離最短.目前,解決ORQ問題的精確算法的基本思想是:首先計算GQ中所有類別的全排列(每個類別在排列中的順序代表此類的訪問順序),并刪除訪問順序不滿足約束條件的排列;然后對于每一個排列,依次從排列的每個類中選擇一個點構成一條路徑;最終枚舉出滿足約束條件的所有路徑,并返回具有最短距離的路徑.然而這些方法在面對基于規則的最短路徑問題時,主要存在以下兩個缺點:(1) 針對基于規則的路徑查詢問題,對圖G進行劃分所得的每個類僅包含一個頂點,即任意兩點對應的類都不相同,已有的算法求解此類問題相當于枚舉出所有滿足約束條件的排列,然而大部分排列對于求解最短路徑來說是冗余的;(2) 目前已有的解決ORQ問題的算法面向的是空間數據庫,這些算法均通過計算兩點之間的歐氏距離加速查詢,然而本文所解決的問題是基于普通的圖模型,兩點間的最短距離即為最短路徑的長度,而存儲全部頂點對之間的最短距離空間開銷過高.因此,本文設計了一種前向擴展算法來快速求解基于規則的最短路徑問題,其主要思想是,盡可能早地過濾掉不能構成最短路徑的子路徑.真實數據集上的實驗結果證明了本文提出的算法的效率遠遠優于傳統ORQ算法.

本文的主要貢獻如下:

(1) 提出了廣義規則樹的概念,設計了生成廣義規則樹的算法,并利用廣義規則樹來判斷算法是否找到一條基于規則的最短路徑;

(2) 設計了基于最優子路徑的前向擴展算法,該算法可以快速求解基于規則的最短路徑問題,并設計了前向擴展算法的改進算法——基于最短優先策略的前向擴展算法;

(3) 在真實的數據集上設計了大量的實驗,并與已有的性能最好的算法比較,實驗結果驗證了本文算法的有效性.

本文第1節給出基于規則的最短路徑查詢問題的形式化定義,并證明此類問題是NP-hard問題.第2節介紹廣義規則樹的概念,并設計生成廣義規則樹的算法.第 3節介紹一種圖數據的預處理技術,可以用來快速求解兩點之間的最短路徑.第 4節和第 5節分別介紹前向擴展算法以及基于最短優先策略的前向擴展算法,并分別對它們的算法復雜度進行分析.第6節在真實的數據集上驗證本文算法的高效性.第7節介紹相關工作.最后一節對全文進行總結.

1 問題定義

有向加權圖可以表示為G(V,E,w)(簡稱G),V表示圖G中全部頂點的集合,E表示全部邊的集合.任意一條有向邊e∈E可以表示為e=(vi,vj),其中,vi,vj∈V,e稱為vi的出邊或者vj的入邊,vj(vi)被稱為vi(vj)的出邊(入邊)鄰居.w是一個權重函數,并且對圖G中的每條邊都賦予一個非負的權重,本文使用wi,j來表示有向邊(vi,vj)∈E的權重,即wi,j=w(vi,vj).圖G中的路徑p是一個頂點序列,即p=(v1,v2,…vk),其中,(vi,vi+1)(1≤i≤k-1)是圖G中的一條有向邊,路徑p的權重用w(p)表示,表示p中全部有向邊的權重之和,即.路徑p是一條簡單路徑當且僅當p中沒有重復的頂點.對于無向圖,一條無向邊(vi,vj)等價于兩條有向邊(vi,vj)和(vj,vi),因此,本文提出的方法也可應用到無向圖上的同類問題.

本文主要研究基于規則的最短路徑查詢問題,首先介紹什么是路徑查詢規則,然后給出基于規則的路徑定義.本文中,路徑規則用R表示,被定義為二元組R=(I,R),包含兩個元素.

(i)I是V的一個頂點子集,即I?V;

(ii)R是一組偏序關系〈vi,vj〉的集合,其中,vi,vj∈I.〈vi,vj〉表示vi?vj.

需要注意的是:偏序關系集R中不存在環,即R中不存在一個偏序關系子集{〈v1,v2〉,…,〈vk-1,vk〉,〈vk,v1〉},其中,頂點v1,v2,…,vk∈I.下面給出基于規則的路徑定義.

定義1.1(基于規則的路徑).給定圖G(V,E,w),起點為vs,終點為ve,規則R=(I,R),如果路徑p滿足以下兩個條件,則被稱為由vs到ve的基于規則R的路徑.

(1) 對每一個頂點vi∈I,都有vi∈p;

(2) 對每一個偏序關系〈vi,vj〉∈R(或者vi?vj),路徑p中都存在一個從vi到vj的子路徑vi?vj.

在定義1.1中,條件(1)是指:若路徑p基于規則R=(I,R),則p需要包含I中的所有點;條件(2)是指:對R中的任意偏序關系vi?vj,在路徑p中都存在一條從頂點vi到頂點vj的子路徑.

給定圖G中的兩個頂點vs,ve以及規則R,從vs到ve的基于規則R的最短路徑表示為,是指從vs到ve的基于規則R的所有路徑中權重w(p)最小的路徑.表1列出了本文常用的符號.

Table 1 List of notations表1 符號列表

例 1.1:給定有向圖G(V,E,w),如圖1(a)所示,已知規則R=(I,R),I={v2,v4,v5,v6},R={v2?v4,v2?v5},其中,起點為v1,終點為v3,可得此圖基于規則R的最短路徑為,如圖1(b)中的虛線箭頭所示.

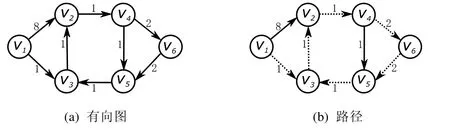
Fig.1 Rule-based shortest path圖1 基于規則的最短路徑

定理1.1.基于規則的最短路徑查詢問題是一個NP-hard問題.

證明:本文通過將其歸約到哈密爾頓路問題(NPC問題)證明.給定一個有向圖G,令vs和ve分別表示起點和終點.G中每條邊的權重都設為1,規則R=(I,R)被設置為I=V-{vs,ve},R=?.顯然,圖G中存在一條從vs到ve的哈密爾頓路當且僅當從vs到ve的基于規則R的最短路徑的長度為|V|-1(|V|表示V中頂點的個數),而且對于一條給定的路徑,不能在多項式時間驗證它是否是基于規則的最短路徑,因此,基于規則的最短路徑問題是一個NP-hard問題.證畢. □

2 廣義規則樹

若p為一條基于規則R的路徑,由第1節可知:在規則R中,偏序關系集R中的偏序關系vi?vj(vi,vj∈I)表示在路徑p中存在一條從vi到vj的子路徑.顯然,對I中的任意一點vi,p中存在一條從起點vs到vi的子路徑,也存在一條vi到終點ve子路徑.由于vs和ve分別為p的起點和終點,因此集合IR=I∪{vs,ve}中的任意點都在基于規則R的路徑p中,稱集合IR為規則點集,IR中的點稱為規則點.本節提出了廣義規則樹的概念,廣義規則樹并非真正的樹,其將規則點集IR中的全部頂點組織成類似樹的結構,并通過樹中的祖先后代關系來表示兩個規則點之間的偏序關系,即:若vi?vj,則在廣義規則樹中,結點vi是結點vj的祖先結點.與普通樹區別在于,廣義規則樹中的結點可能具有多個父親結點.利用廣義規則樹,本文提出的算法可以高效判斷搜索到的路徑p是否是一條滿足規則的路徑.下面首先給出廣義規則樹的定義,然后給出廣義規則樹的生成算法.

定義2.1(廣義規則樹).滿足規則R的廣義規則樹是一棵由規則點集IR中全部頂點構成的廣義樹,記為TR,其滿足以下兩個條件.

(1) 起點vs為根結點、終點ve為唯一葉結點;

(2) 對TR中除根結點和葉結點外的任意兩個結點vi,vj,若vi是vj的一個父親結點,當且僅當vi?vj;且不存在另外一個頂點vk∈I,使得vi?vk和vk?vj同時成立.

廣義規則樹滿足以下兩個性質.

性質2.1.給定起點vs、終點ve和規則R,廣義規則樹TR存在且唯一.

證明:當給定起點vs和終點ve,TR的根和唯一葉結點即已確定.給定規則R,TR中結點的父親-孩子關系也已確定,故TR存在且唯一.證畢. □

性質2.2.R中蘊含的任意一個偏序關系都對應廣義規則樹中的一對祖先后代結點.證明:若R中蘊含vi?vj,由廣義規則樹定義中的條件(2)可知:在TR中,vi是vj的祖先結點.證畢. □顯然,在廣義規則樹中,起點是所有其他點的祖先結點,終點是所有其他點的后代結點.規則點vi∈IR的全部父結點集合表示為,子結點集合表示為,祖先結點集合表示為,后代結點集合表示為.例 2.1給出了廣義規則樹的示例.

例 2.1:給定有向

圖G,如圖1(a)所示,其中,起點為v1,終點為v3,規則R=(I,R),I={v2,v4,v5,v6},若R=?,則基于規則R的廣義規則樹如圖2(a)所示;若R={v2?v4,v2?v5},此基于規則R的廣義規則樹如圖2(b)所示.

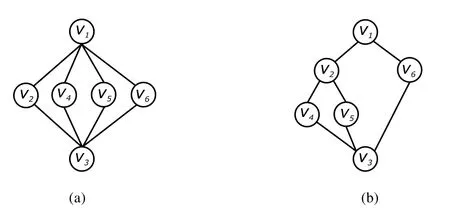
Fig.2 Generalized rule tree圖2 廣義規則樹

下文中,規則點vi∈IR的父結點、子結點、祖先結點和后代結點均指廣義規則樹中對應樹結點vi的父結點、子結點、祖先結點和后代結點.例如在圖2(b)中,規則點v2的父結點集合、子結點集合、祖先結點集合、后代結點集合.

算法1展示了構造廣義規則樹的偽代碼.初始階段,算法將所有的規則點初始化一棵廣義樹(第1行),廣義樹的根設為起點vs,唯一葉結點設為終點ve,I中的所有頂點都互為兄弟結點,且它們的父結點和祖先結點都設為vs,子結點和后代結點都設為ve,因此,vs的子結點集合和ve的父結點集合均為I.算法1的主要思想是:依次處理R中的每一對偏序關系,并逐步構造廣義規則樹.在每次迭代中,對每個〈vi,vj〉∈R,算法判斷在TR中vi是否是vj的祖先:若是,則忽略〈vi,vj〉并跳出本輪迭代(第 3行～第 3行);否則,根據〈vi,vj〉更新廣義規則樹TR.更新過程如下.

· 首先,對TR中vi的每個子結點,若vk是vj的后代結點,則將vk從中刪除(第6行～第10行);對TR中vj的每個父結點,若vk是vi的祖先結點,則將vk從中刪除(第11行～第15行);

· 然后,將vi加入vj的父結點集合,將vj加入vi的子結點集合(第16行);

· 最后,對vj的每個祖先結點vk,將vk的后代結點集合更新為(第 17行～第 19行);對vi的每個祖先結點vk,將vk的祖先結點集合更新為(第 20行～第22行).當R中的全部偏序關系處理完畢,算法結束并返回TR.

算法1.GeneralizedRuleTree(G,vs,ve,R).

輸入:圖G,起點vs,終點ve,規則R=(I,R);

輸出:廣義規則樹TR.

例2.2:接例1.1,利用算法1構造其對應的廣義規則樹.首先,初始化廣義規則樹,結果如圖3(a)所示;當偏序關系v2?v4插入到廣義樹中后,結點v2的子結點集合修改為{v4},結點v4的父結點集合修改為{v2},結點v1的子結點集合修改為{v2,v5,v6},結點v3的父結點集合修改為{v4,v5,v6},結果如圖3(b)所示;當偏序關系v2?v5插入到廣義樹中后,結點v2的子結點集合修改為{v4,v5},結點v5的父結點集合修改為{v2},結點v1的子結點集合修改為{v2,v6},結果如圖3(c)所示.

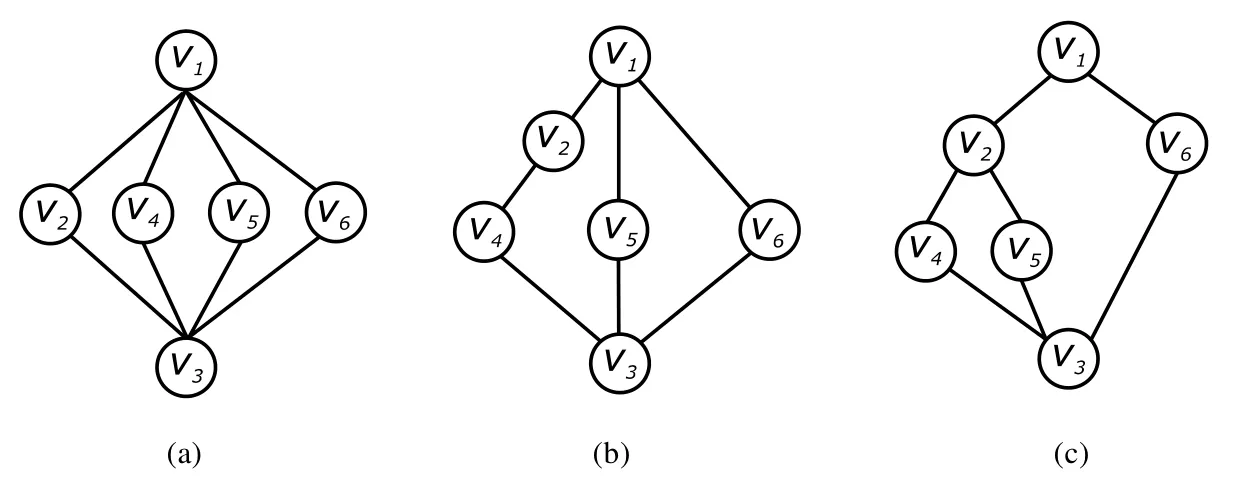
Fig.3 Construction of generalized rule tree圖3 廣義規則樹的構造過程

廣義規則樹TR中,結點vi被某路徑p合法訪問是指:若vi為根結點,則p包含vi;否則,p包含vi且vi在TR中的所有父結點都已被p中從起點vs到vi的子路徑合法訪問.定理2.1給出了路徑p是否滿足規則R的判斷條件.

定理2.1.路徑p為一條從起點vs到終點ve的路徑,若終點ve被路徑p合法訪問,則路徑p為一條基于規則R的路徑.

證明:由規則點被路徑合法訪問的定義可知,集合I中的點都在路徑p中.下面證明偏序關系集R中的所有偏序關系均已滿足.假設存在一個偏序關系〈vi,vj〉∈R,使得p不滿足此偏序關系,即p中不存在一條從vi到vj的子路徑,因此,規則點vj沒有被合法訪問且vj的所有子結點也沒有被合法訪問.由于終點ve是所有規則點的后代結點,可得終點ve沒有被路徑p合法訪問.這與已知條件矛盾.因此,所有的偏序關系均已滿足.綜上可得,路徑p為一條基于規則R的路徑.證畢. □

由定理2.1可知:可以依據一個查詢的終點是否被一條路徑合法訪問,來判斷此路徑是否為基于規則的路徑.在下文介紹的前向擴展算法中,本文依據定理2.1來判斷是否已找到一條基于規則的路徑.

3 分層收縮技術

分層收縮(contraction hierarchies,簡稱 CH)[12]是一種簡單有效的圖數據預處理技術,它可以提高最短路徑的查詢效率.CH本質上是預先存儲一些最短路徑信息,從而實現加速最短路徑查找的目的.本文采用CH技術進行預處理,以使算法能更高效地計算兩點之間的最短路徑.給定圖G(V,E,w),CH首先給V中所有頂點分配一個序號,任意兩個頂點的序號都不相同;然后依據序號的大小,按照從小到大的順序對點進行收縮.頂點vi被收縮是指:把vi以及與vi相連的邊從G中刪除,并且添加一些新的邊到G中.具體地,對每一對vi的入邊(vj,vi)和出邊(vi,vk),如果路徑(vj,vi,vk)是連接vj和vk的唯一的最短路徑,則往G中添加邊(vj,vk),并且將邊(vj,vk)的權重設為(vj,vi)和(vi,vk)的權重之和.所有頂點收縮完成之后,CH將原圖G分為兩個新圖,分別為前向圖Gu和后向圖Gd;然后,CH利用Gu和Gd計算最短路徑.CH技術的具體細節見文獻[12].

4 FE算法

本節提出前向擴展算法(forward expanding,簡稱 FE)來求解基于規則R的最短路徑.接下來,首先介紹最優子排列,然后詳細介紹FE算法,最后分析了算法的時間和空間復雜度.

4.1 最優子排列

給定有向圖G(V,E,w)、規則R=(I,R)以及起點vs和終點ve,可得規則點集IR,令r表示IR中點的個數,即r=|IR|.IR的一個排列π是一個點序列v1v2…vr,對任意點vi(1≤i≤r)都有vi∈IR,且排列π中不包含重復的點.顯然,一個規則點集IR總共有r!個排列.對于一個排列π,本文用規則點在π中的次序來表示此規則點在路徑p中的合法訪問順序,即:若vi∈IR在π中處于第i個位置,則在p中,vi是第i個被合法訪問的.給定排列π=v1v2…vr,如果路徑p滿足下面3個條件,稱p為一條對應于π的路徑,記為p|π.

(1) 對π中任意點vi,p中都包含點vi;

(2) 若π中點vi的位置在vj之前,則p中包含一條從vi到vj的子路徑;

(3) 路徑p的起點和終點分別為v1和vr.

給定路徑p|π,它可以被π中的所有點劃分為r-1條子路徑.每條子路徑都被稱為p|π的一個路徑片段.本文使用Sp|π來表示p|π的所有路徑片段.

定義4.1(基于規則的排列).給定圖G(V,E,w),起點為vs,終點為ve,規則R=(I,R),π是規則點集IR的一個排列.已知條件:(1)π起始位置和末尾位置的頂點分別為vs和ve;(2) 對每一個偏序關系〈vi,vj〉∈R(或者vi?vj),π中vi的位置都在vj之前.若排列π滿足上述兩個條件,則稱π為從vs到ve的基于規則R的排列.所有基于規則R的排列構成的集合記為,即,中所有排列都以vs為起始位置頂點、ve為末尾位置頂點且滿足規則R.

由定義4.1可知:若π為一個基于規則R的排列,則p|π為一個基于規則R的路徑.如果路徑p是對應于排列π的路徑,且p中的所有路徑片段均為最短路徑,本文稱p為對應于排列π的最短路徑,記為p*|π.由此可以得到下面的定理:

定理4.1.給定圖G(V,E,w),起點為vs,終點為ve,規則R=(I,R),若p*是IR的所有基于規則的排列所對應的p*|π中權重最小的一條路徑,則p*即為基于規則R的最短路徑.

證明:給定IR的一個基于規則R的排列π,因為p*|π中的所有路徑片段都是最短路徑,因此p*|π的權重不大于π所對應的每一條路徑p|π的權重;又因為p*是所有基于規則的排列所對應的p*|π中權重最小的一條路徑,而且所有的p*|π都是基于規則R的路徑,因此,p*為基于規則R的最短路徑.證畢. □

由定理4.1可知:對于一個基于規則的排列π,只有當π所對應的路徑p|π中的所有路徑片段都為最短路徑時,即p|π為p*|π,此路徑才有可能成為基于規則的最短路徑.因此,本文后續部分所提到的任意排列π所對應的路徑都特指p*|π,即所有的路徑片段都為最短路徑.

對于點集Vs?V,可以逐步擴展點序列的長度來得到Vs的排列,其中,點序列中的每個點都屬于Vs,且點序列中不包含重復的頂點.如果點序列中包含l個頂點,本文稱此點序列為Vs的l-子排列(特別地,本文規定:規則點集IR的所有子排列均以起點vs作為起始位置的頂點),記為πl,其中,1≤l≤r(r=|Vs|).包含πl中l個頂點的點集合稱為子排列πl對應的點集,記為Vπl.給定一個排列π,π⊕v表示π擴展一個頂點后形成的新排列,這稱為排列的擴展操作,其中,⊕是一個連接符,即,把點v添加到π的末尾.若πl1和πl2分別為Vs的l1-子排列和l2-子排列,已知條件:(1)l1≤l2;(2)πl2經由πl1擴展 0個或多個頂點得到.如果πl1和πl2滿足條件(1)和條件(2),則稱πl1為πl2的前綴.例如,v1v2是v1v2v3v4的前綴.下面本文給出子排列滿足的規則的定義.

定義4.2(子排列滿足的規則R′=(I′,R′)).給定圖G(V,E,w),起點為vs,終點為ve,規則R=(I,R),πl為IR的l-子排列(1≤l≤|IR|)且πl起始位置的頂點為vs.R′=(I′,R′),其中,I′?I,R′?R,已知條件:(1)πl是I′的一個排列;(2) 對任意偏序關系〈vi,vj〉∈R′,都有vi,vj∈I′且πl中vi的位置在vj之前;(3) 不存在偏序關系〈vi,vj〉∈R-R′,使得vi,vj∈I′.若規則R′滿足上述3個條件,則稱R′為子排列πl滿足的規則.

利用定義4.2,可以很容易地給出最優子排列定理.

定理4.2.給定圖G(V,E,w),起點為vs,終點為ve,規則R=(I,R),若IR的排列π對應的路徑p|π為基于規則R的最短路徑,πl為π的包含l(1≤l≤|IR|)個頂點的前綴,πl滿足的規則為R′=(I′,R′),v*是πl末尾位置的頂點,對任意排列,都有,本文稱πl為IR的一個最優子排列.

給定有向圖G(V,E,w)如圖1(a)所示,已知規則,起點為v1,終點為v3,可得排列對應的路徑為基于規則R的最短路徑,為π的包含4個頂點的前綴,v6是π4末尾位置的頂點,π4滿足的規則為R′=(I′,R′),其中,,π4和π4′分別對應的路徑為.顯然,

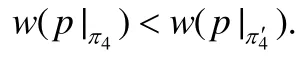
推論4.1.給定圖G(V,E,w),起點為vs,終點為ve,規則R=(I,R),已知IR的長度為l(1≤l≤|IR|)的一個子排列πl,πl起始位置的頂點為vs、末尾位置的頂點為v*,πl滿足的規則為R′=(I′,R′),則擴展操作得到的子排列集合中,存在一個子排列′,使得對任意的,都有,IR的排列π對應的路徑p|π為基于規則R的最短路徑,若π的長度為l的前綴屬于,將π的長度為l的前綴替換為′得到新的排列π′,則w(p|π′)=w(p|π),本文稱πl′為IR的一個最優子排列.

4.2 前向擴展算法

本節提出求解基于規則R的最短路徑的前向擴展算法,算法的主要思想是:從規則點集IR的 1-子排列逐步進行擴展操作直至IR的r-子排列(r=|IR|),并利用最優子排列對生成的子排列進行過濾,最終返回IR的r-子排列對應的路徑中權重最小的那條路徑.

前向擴展算法的偽代碼見算法2.

算法2.FE(G,vs,ve,R).

輸入:圖G,起點vs,終點ve,規則R=(I,R);

給定圖G(V,E,w),起點為vs,終點為ve,規則R=(I,R),FE首先調用算法 1得到廣義規則樹TR(第 1行);然后,利用下文相關工作部分介紹的啟發式算法NN求解得到基于規則R的路徑pg,令θ等于pg的權重(第2行、第2行);第4行～第 24行,FE逐步擴展規則點集IR的 1-子排列直至IR的r-子排列(r=|IR|).在構建IR的 1-子排列時,因為只有π1=vs這一個1子排列滿足規則,因此,FE將R1初始化為{vs}(第4行、第5行);第6行～第24行,FE循環得到IR的2-子排列至r-子排列.下面將詳細介紹FE求解IR的l-子排列的過程,其中,2≤l≤r.

FE用Rl來存儲IR的l子排列所對應的路徑:首先,將Rl初始化為空集(第7行);然后,FE對長度為l-1的子排列進行擴展操作,并利用最優子排列理論過濾不可能成為基于規則的最短路徑所對應排列的前綴.依據子排列πl-1對應的點集Vπl-1,FE將Rl-1劃分為不同的集合,即屬于同一集合里的路徑擁有相同的點集Vπl-1,屬于不同集合的路徑擁有不同的點集Vπl-1(第8行).接下來,FE依次遍歷規則點集IR中除vs之外的其他所有點(第9行),并對每一個v∈IR-{vs}做如下操作:遍歷劃分Rl-1得到的每一個集合中的每一條路徑都與一個長度為l-1的子排列所對應,對于Rl′-1中的每一條路徑p|πl-1及相應的πl-1,如果πl-1中不包含點v且v的所有父結點均已被p|πl-1合法訪問,那么將v添加到πl-1的末尾構成長度為l的子排列πl并且生成相應的路徑p|πl,若中的每一條路徑均已完成上述操作,則從新生成的路徑中選擇一條權重最小的路徑,記為即為一個最優子排列,如果p*|πl的權重不大于θ,則將p*|πl添加到Rl中(第10行～第22行).

FE求得IR的r-子排列所對應的路徑之后,由于IR的r子排列所對應的路徑的最后一個頂點為終點ve,由定理2.1可知,IR的r子排列所對應的路徑都為基于規則R的路徑,顯然,基于規則R的最短路徑即為IR的r子排列所對應的路徑中權重最小的一條.第25行、第26行,FE首先遍歷Rr得到具有最小權重的路徑,然后返回此路徑作為基于規則R的最短路徑.

例4.1:接例 1.1,利用 FE算法求解基于規則R的最短路徑的過程見表2,其中,πl表示一個子排列,|πl|表示子排列中包含頂點的個數,Vπl表示πl對應的點集,v*表示πl的最后一個頂點,p|πl表示πl所對應的路徑.用貪心算法求解得到基于規則R的路徑pg=(v1,v3,v2,v4,v5,v3,v2,v4,v6,v5,v3),θ=w(pg)=12.加刪除線的子排列表示被最優子排列過濾掉的子排列,從表2的結果可得,最優子排列可以減少算法在求解過程中生成的子排列個數,從而降低算法的求解時間.FE算法最終得到的排列為π=v1v2v4v6v5v3,所對應的路徑為p|π=(v1,v3,v2,v4,v6,v5,v3),w(p|π)=8,因此,p|π即為基于規則R的最短路徑.

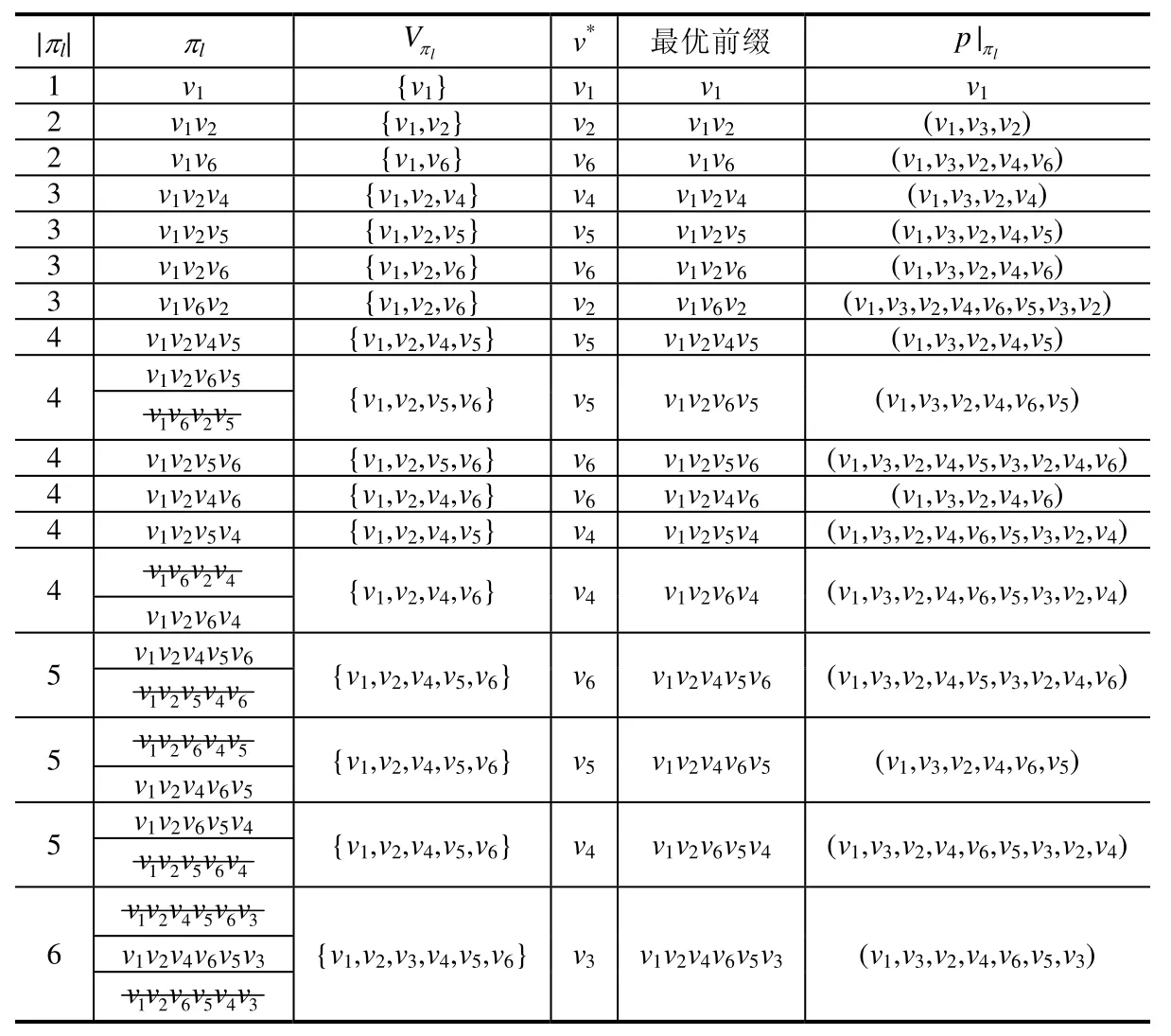
Table 2 Solving process of FE algorithm表2 FE算法的求解過程

4.3 復雜度分析

4.3.1 時間復雜度.

FE的時間復雜度主要集中在計算IR的長度為1至r(r=|IR|)的子排列上,對于長度為l(1≤l≤r)的子排列,由最優子排列可知,FE至多生成個,其中,表示IR中頂點的組合數.因此,FE至多生成個子排列.本文采用 CH技術求解兩點之間的最短路徑,它的時間復雜度為O(nlogn+m)(n=|V|,m=|E|),因此,FE的時間復雜度為O((nlogn+m)·(r·2r)).

4.3.2 空間復雜度.

FE需要利用長度為l-1的子排列來求解長度為l的子排列,因為FE至多生成個長度為l(2≤l≤r)的子排列,因此在求解長度為l的子排列時,內存的總消耗為;一旦求得長度為l的子排列之后,即可將存儲長度為l-1的子排列的內存釋放.因此,FE所消耗的內存最大為,即,FE 的空間復雜度為O(n·r·2r).

5 FEBF算法

本節提出 FE算法的改進算法——基于最短優先策略的前向擴展算法(forward expanding based on best-first searching,簡稱 FEBF).接下來,本文首先分析如何對 FE算法進行改進;然后給出基于最短優先策略的前向擴展算法,并對算法做出詳細的介紹;接著,對FEBF算法提出了幾個優化技術;最后,分析了FEBF算法的時間和空間復雜度.

5.1 基于最短優先策略的前向擴展算法

從第4.2節可知,FE算法依次擴展規則點集IR的長度為1至長度為r(r=|IR|)的子排列,最后從長度為r的子排列對應的路徑中選擇權重最小的路徑作為問題的解.在求解長度為l的子排列時,FE必須先求得長度為l-1的所有子排列.事實上,某些長度為l-1的子排列所對應路徑的權重已大于基于規則R的最短路徑的權重,因此沒有必要對這部分子排列進行擴展操作.在例4.1中長度為3的子排列v1v6v2對應路徑為(v1,v3,v2,v4,v6,v5,v3,v2),其權重為9,而基于規則R的最短路徑權重為8,因此,沒有必要再對子排列v1v6v2進行擴展操作.基于此,本文提出基于最短優先策略來逐步擴展路徑的算法,算法的主要思想是:在對子排列進行擴展操作時, FEBF首先從已有的子排列中選擇一個對應路徑的權重最小的一個子排列,然后對它進行擴展操作,并得到對應的路徑,所有規則點擴展結束之后,FEBF刪除這個子排列,然后重復上述操作,直至找到一個基于規則R的排列,它所對應的路徑即為基于規則R的最短路徑.

FEBF算法本質上也是逐步擴展IR的長度為1的子排列到長度為r的子排列,它采用最短優先的策略盡可能少地計算IR的子排列,從而可以盡快找到問題的解.FEBF算法的偽代碼見算法3.

算法3.FEBF(G,vs,ve,R).

輸入:圖G,起點vs,終點ve,規則R=(I,R);

給定圖G(V,E,w),起點為vs,終點為ve,規則R=(I,R),FEBF利用優先級隊列實現從已有子排列中選出具有最小權值的路徑及其相應的子排列.算法首先定義優先級隊列Q,Q中存儲的元素為二元組,記為〈π,w(p|π)〉,其中,π為IR的子排列,并用w(p|π)的值進行優先級比較,以實現對Q中的元素從小到大進行排序(第1行).接下來調用算法1得到廣義規則樹TR(第2行),然后用NN算法求解得到基于規則R的路徑pg,令θ等于pg的權重(第3行、第4行).為了利用最優子排列過濾子排列,FEBF逐步構建最優子排列表(記為Ω)來存儲已得到的最優子排列.當擴展得到子排列πl時,FEBF首先查找最優子排列表中對應位置的元素(記為,其中,v*為πl末尾位置的頂點,Vπl為子排列πl對應的點集),然后對和w(p|πl)進行比較:若,則將的值設為w(p|πl) 且保留子排列πl并對其進行后續操作;否則,刪除子排列πl.FEBF將最優子排列表中每一個元素的值都初始化為∞(第 5行).接下來,FEBF將逐步擴展子排列直至找到基于規則R的排列(第6行～第20行).

在構建IR的1-子排列時,因為只有π1=vs這一個1子排列滿足規則,因此,FEBF將 〈π1,w(p|π1)〉插入到優先級隊列Q中(第 6 行、第 7 行),然后彈出Q的隊首元素〈π′,w(p|π′)〉,令v*為π′末尾位置的點(第 8 行).如果v*=ve(第 9行),則表示π′是一個基于規則R的排列(由定理2.1可得),又因為Q每次彈出的位于隊首的元素都具有最小的路徑權重,因此,p|π′即為基于規則R的最短路徑,FEBF返回此路徑作為問題的解(第 21行、第 22行);否則(v*≠ve),執行以下循環操作(第10行～第19行).首先,FEBF依次遍歷規則點集IR中除vs之外的其他所有點(第10行),然后對每一個v∈IR-{vs}做如下操作:如果π′中不包含點v且v的所有父結點均已被p|π′合法訪問,那么將v添加到π′的末尾構成新的子排列π,若Ωv,Vπ＞w(p|π),則將Ωv,Vπ的值設為w(p|π),并將〈π,w(p|π)〉插入到Q中(第11行～第17行).若IR-{vs}中的每個點均已完成上述操作,則 FEBF 彈出Q的隊首元素〈π′,w(p|π′)〉,令v*為π′末尾位置的點(第19行),然后開始下一輪循環.

例5.1:接例1.1,利用FEBF算法求解基于規則R的最短路徑.

FEBF首先生成〈v1,0〉并把它插入到優先級隊列Q中,接下來的操作是:從Q中彈出〈v1,0〉,利用它擴展得到〈v1v2,2〉,〈v1v6,5〉并分別插入到Q中;

從Q中彈出〈v1v2,2〉,利用它擴展得到〈v1v2v4,3〉,〈v1v2v5,4〉,〈v1v2v6,5〉并分別插入到Q中;從Q中彈出〈v1v2v4,3〉,利用它擴展得到〈v1v2v4v5,4〉,〈v1v2v4v6,5〉并分別插入到Q中;從Q中彈出〈v1v2v5,4〉,利用它擴展得到〈v1v2v5v4,7〉,〈v1v2v5v6,9〉并分別插入到Q中;從Q中彈出〈v1v2v4v5,4〉,利用它擴展得到〈v1v2v4v5v6,9〉并插入到Q中;從Q中彈出〈v1v6,5〉,利用它擴展得到〈v1v6v2,9〉并插入到Q中;

從Q中彈出〈v1v2v6,5〉,利用它擴展得到〈v1v2v6v4,10〉, 〈v1v2v6v5,7〉并分別插入到Q中;

從Q中彈出〈v1v2v4v6,5〉,利用它擴展得到〈v1v2v4v6v5,7〉并插入到Q中;

從Q中彈出〈v1v2v5v4,7〉,利用它擴展得到〈v1v2v5v4v6,9〉并插入到Q中;

從Q中彈出〈v1v2v6v5,7〉,利用它擴展得到〈v1v2v6v5v4,10〉并插入到Q中;

從Q中彈出〈v1v2v4v6v5,7〉,利用它擴展得到〈v1v2v4v6v5v3,8〉并插入到Q中;

從Q中彈出〈v1v2v4v6v5v3,8〉且滿足路徑搜索終止條件,此時算法終止,FEBF返回(v1,v3,v2,v4,v6,v5,v3)作為問題的解.

在例4.1中,FE算法總共生成24個子排列;而在例5.1中,FEBF總共生成18個子排列.顯然,FEBF能有效減少算法生成的子排列個數.

5.2 優化技術

本節提出3個優化技術來提高FEBF算法的效率.

· 緩存機制

給定IR的基于規則R的兩個不同排列π和π′,這兩個排列對應的路徑p*|π′和p|π′可能包含一些相同的路徑片段,因此這些相同的路徑片段本質上只需要計算一次.本文可以采用緩存機制,將計算過的路徑片段存儲在內存中,這樣就可以避免大量重復的計算,從而提高算法的效率.比如在例 4.1中,長度為 6的排列v1v2v4v6v5v3和v1v2v4v6v5v3所對應的路徑包含相同的路徑片段v1?v2和v2?v4,因此當采用緩存機制后,這兩個路徑片段僅僅只需要計算一次,當再次需要計算這兩個路徑片段時,可以直接從緩存中讀取出來.實驗結果驗證了緩存機制可以有效避免大量的冗余計算.

· 排列過濾

當 FE對長度為l-1的子排列πl-1進行擴展操作時,它首先判斷規則點v∈IR是否已在πl-1中,然后再判斷v的所有父結點是否已被路徑合法訪問,若上述兩個條件都滿足,則將v添加到πl-1的末尾構成長度為l的子排列πl.上述兩個條件本質上是從規則點v是否應該被合法訪問這個角度判斷v是否應該添加到πl-1的末尾,本文也可以從路徑權重的角度來進一步過濾生成的排列,即:已知vi,vj∈IR且vj已被添加到πl-1的末尾構成πl-1⊕vj,v*是πl-1末尾位置的頂點,如果v*到vj的最短路徑是v*到vi最短路徑的子路徑,則vi不應被添加到πl-1的末尾構成πl-1⊕vi.下面的定理保證了排列過濾的正確性.

定理5.1.給定長度為l-1 的子排列πl-1,v*是πl-1末尾位置的頂點,已知vi,vj∈IR,πl-1⊕vj和πl-1⊕vi分別為 FE用vj和vi對πl-1進行擴展操作得到的長度為l的子排列,如果v*到vj的最短路徑是v*到vi最短路徑的子路徑,則IR的所有基于規則R且以πl-1⊕vi為前綴的排列π都對應一個IR基于規則R且以πl-1⊕vj為前綴的排列π′,且w(p|π′)≤w(p|π).

證明:不失一般性,設πl-1=v1v2…v*是IR的長度為l-1 的子排列,πl-1⊕vj和πl-1⊕vi分別為 FE 用vj和vi對πl-1進行擴展操作得到的長度為l的子排列,已知v*到vj的最短路徑是v*到vi最短路徑的子路徑.

綜上可得w(p|π′)≤w(p|π).證畢.□

在例4.1中,對于長度為2的子排列v1v2,可以分別用點v4,v5,v6對v1v2進行擴展操作,從而得到v1v2v4,v1v2v5,v1v2v6.因為從v2到v4的最短路徑(v2,v4)是從v2到v5最短路徑(v2,v4,v5)的子路徑,也是從v2到v6最短路徑(v2,v4,v6)的子路徑,因此可以過濾掉子排列v1v2v5和v1v2v6.

· 權重預估

當 FE擴展長度為l-1的子排列得到長度為l的子排列πl時,v*是πl末尾位置的頂點.對于IR的所有基于規則R且以πl為前綴的排列π,可以估計w(p|π)的下限,從而使得FE可以盡量早的過濾掉一些排列,提高算法的效率.具體的做法是:當得到πl后,首先計算w(p|πl) ,然后計算從v*到終點ve的最短路徑的權重,然后得到這兩個路徑的權重之和w*,若w*>θ,則舍棄子排列πl;否則保留πl.

5.3 復雜度分析

本文首先分析FEBF的時間復雜度,對于長度為l(1≤l≤|IR|)的子排列,FEBF至多生成個,因為本文采用CH技術求解兩點之間的最短路徑,因此,FEBF的時間復雜度為O((nlogn+m)·(r·2r))(n=|V|,m=|E|);接下來分析算法的空間復雜度,FEBF的優先級隊列Q中至多存儲O(r·2r)個元素,每個元組至多消耗的內存為O(n),除此之外,最優子排列表Ω消耗的內存至多為O(r·2r),因此,FEBF 的空間復雜度為O(n·r·2r+r·2r)=O(n·r·2r).

6 實驗分析

本節使用不同規模的真實數據集來驗證算法的有效性,并與解決同類問題中已有的最好算法作對比.第6.1節介紹了實驗的基本設置,第6.2節對實驗的結果進行分析.

6.1 實驗設置

本文的所有算法都使用 C++語言實現,并在 Linux操作系統環境下進行測試,硬件的信息為:Intel(R)Core(TM) i7-4770K,32GB RAM.本文對每組實驗重復100次,并把平均值作為此組實驗的結果.如果一個算法在某個數據集上的運行時間超過24h或者超過32GB RAM,則忽略此算法在這個數據集上的運行結果.

· 數據集

本文使用8個真實數據集來驗證本文提出的算法,其中4個為道路交通網數據集(http://www.dis.uniroma1.it/challenge9/index.shtml),另外 4個為非道路交通網數據集(http://snap.stanford.edu/data/),數據集的詳細信息見表3,d表示頂點的平均度的大小.對于道路交通網數據集,本文將兩點之間的距離作為邊的權重;對于非道路交通網數據集,本文給每一條邊隨機生成一個1～100之間的值作為此邊的權重值.

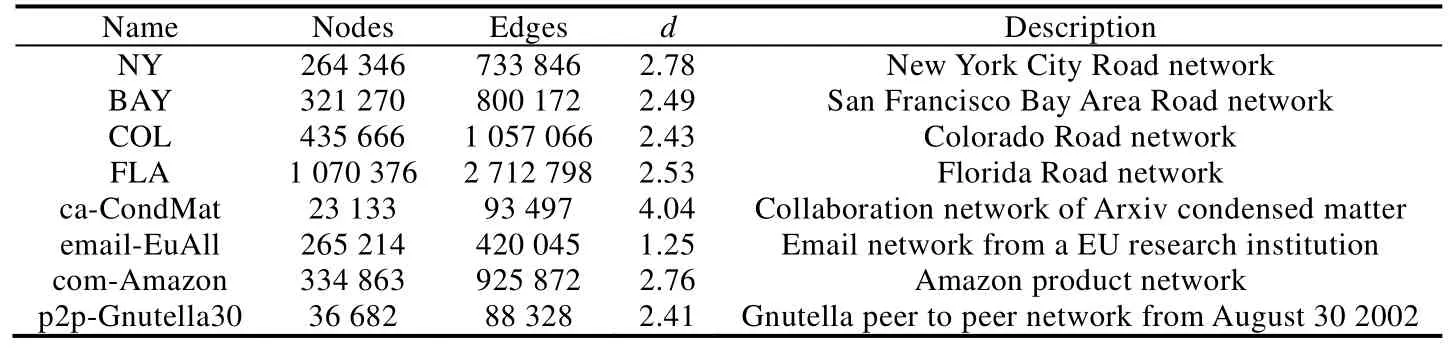
Table 3 Datasets表3 數據集

· 查詢集

對于每個數據集,本文生成25個查詢集 Q1～Q25,它們分別對應不同規模的規則R.在現實生活中,I的規模一般不超過10,本文從實際應用的角度設計了以下的查詢集.對于Q1～Q5,|R|=5,I中頂點的個數依次為6～10;對于 Q6～Q10,|I|=8,R中偏序關系個數依次為 4,6,8,10,12;對于 Q11～Q15,R=?,I中頂點的個數依次為 6～10;對于Q16～Q20,I中頂點的個數依次為6～10,對應的R中偏序關系個數依次為15,21,28,36,45;對于Q21～Q25,|R|=10,I中頂點的個數依次為 16～20.注意到:查詢集 Q11～Q15中偏序集個數為 0,此問題退化為廣義旅行商問題;Q16～Q20中的偏序集可以構成一個全序集,即I中頂點的合法訪問順序已確定,此問題退化為最優序列路徑查詢問題.Q21～Q25中規則R的規模較大,是用來驗證算法能否應用于輸入規模較大的情形.對于上述所有的查詢集,I中所有的頂點以及起點vs和終點ve都是采用隨機數的方式隨機生成,R中偏序關系也是隨機從對應的I中選擇兩個點構成且保證R中不存在兩個相同的偏序關系.

· 對比算法

對每一組實驗,本文將算法FE、FEBF與算法SBS和SFS作對比,SBS[13]和SFS[13]是同類問題的已有算法中性能最好的精確算法.本文不與其他的算法對比的原因是:(1) BBS[13]和BFS[13]分別為SBS和SFS的優化算法,主要是解決當I中包含的不是點而是類別信息時,隨著每個類中包含頂點的個數增多,導致搜索空間增大的問題,當每個類中只包含一個頂點時,優化前后的算法性能相同;(2) NN[14]是一個啟發式算法,它最終返回的路徑是一條接近最優的路徑,而本文的算法返回的是一條最優的路徑.

· 其他

由于SBS和SFS都為應用于空間數據集上的算法,在空間數據集上可以直接利用經緯度坐標求得兩點之間的歐氏距離,而本文所設計的算法均應用于普通的圖數據,即,由點和邊構成的數據,考慮到對比的公平性,本文對所有的算法均利用CH技術來求解兩點之間的最短距離.

6.2 結果分析

· 查詢效率

在查詢集Q1～Q5上算法的運行結果如圖4所示.可以看出:對于每一個數據集,SFS的查詢時間都大于其他算法的查詢時間,FE算法的查詢時間明顯小于SBS和SFS的查詢時間,FEBF算法的查詢時間小于其他所有算法,即使在具有百萬個頂點的數據集(FLA)上,FEBF也能在 1s左右得到查詢的結果.因為查詢集 Q1～Q5具有相同個數的偏序關系,隨著規則點集的規模逐漸增大,規則點集的基于規則R的排列也逐漸增多,因此算法的查詢時間也逐漸增多,圖中的結果驗證了這一點,即:從 Q1～Q5,所有算法的查詢時間都逐漸增多.顯然,改進后的FEBF算法比原始的FE算法性能有較大的提高.

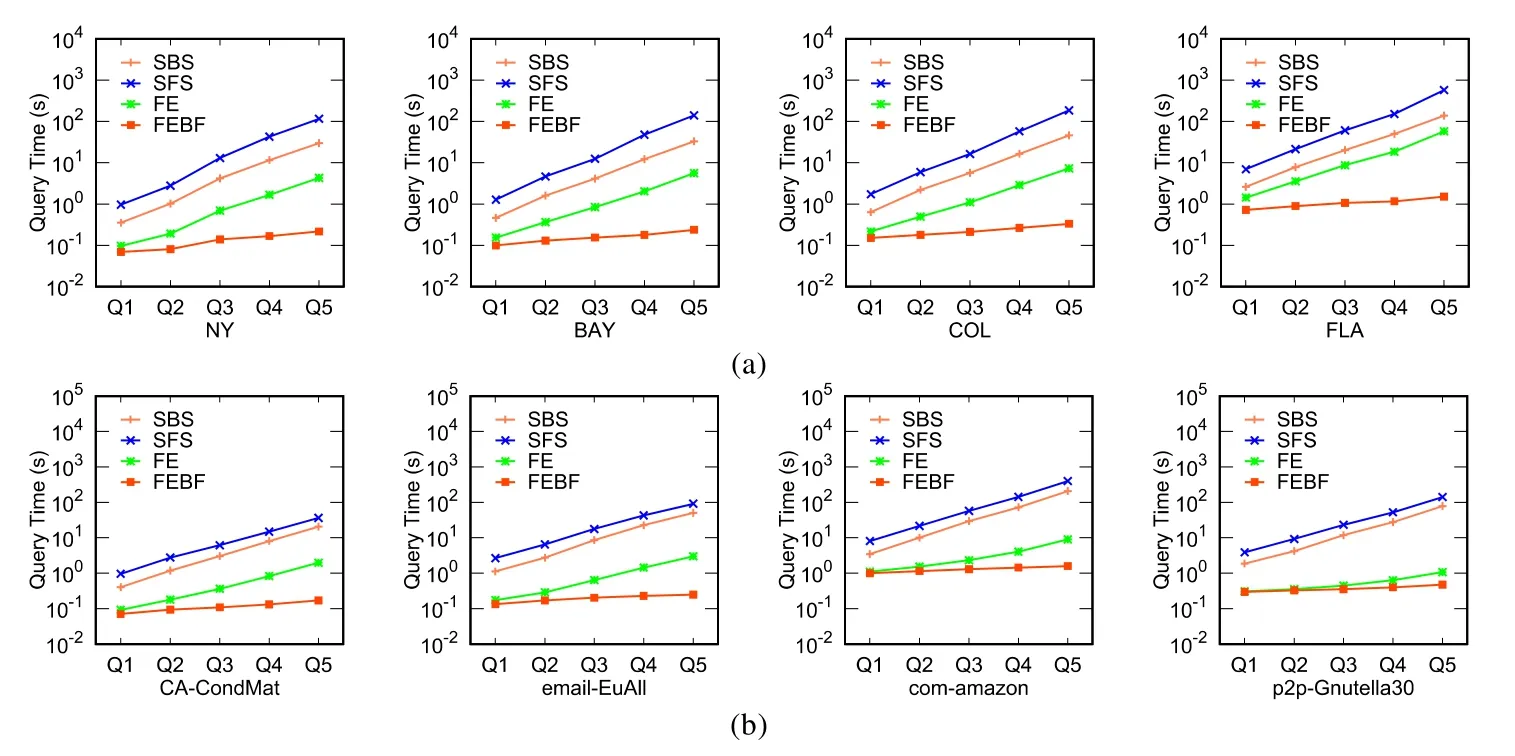
Fig.4 Query efficiency on Q1～Q5圖4 在Q1～Q5上的查詢效率

圖5展示了算法在查詢集Q6～Q10上的查詢結果.對于所有的數據集,SFS具有最大的查詢時間,FEBF算法的查詢時間小于其他所有算法.因為查詢集Q6～Q10具有相同個數的規則點,隨著R中偏序關系的逐漸增多,規則點集的基于規則R的排列將逐漸減少.可以看出對于所有算法,Q6～Q10的查詢時間都逐漸減小.

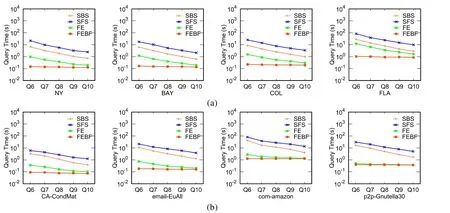
Fig.5 Query efficiency on Q6～Q10圖5 在Q6～Q10上的查詢效率

查詢集Q11～Q15中包含的偏序關系個數為0,此問題退化為廣義旅行商問題,算法的查詢結果如圖6所示.因為 Q11～Q15的偏序關系個數為 0,則規則點集的任意排列都為基于規則R的排列,算法的查詢時間顯然大于在Q1～Q5上的查詢時間.對于每一個數據集,FEBF的查詢時間都小于其他算法的查詢時間.

Fig.6 Query efficiency on Q11～Q15圖6 在Q11～Q15上的查詢效率

查詢集Q16～Q20的偏序集可以構成一個全序集,即I中頂點的合法訪問順序已確定,此問題退化為最優序列路徑查詢問題,算法的查詢結果如圖7所示.由于每個類中僅包含一個頂點,因此,Q16～Q20本質上為計算|I|+1個最短路徑.從圖中可知:對于每一個數據集,SBS算法的查詢時間都是最短的.這是因為SBS沒有利用其他的優化策略來過濾子排列,而對于Q16～Q20來說,基于規則R的子排列只有一個,因此,SBS可以快速地求解得到問題的解.FE和FEBF算法由于利用了一些過濾子排列的優化技術(Q16～Q20并不需要對子排列進行過濾),從而增加了算法的運行時間.然而在現實生活中,這種查詢幾乎不存在(退化為普通的最短路徑問題).

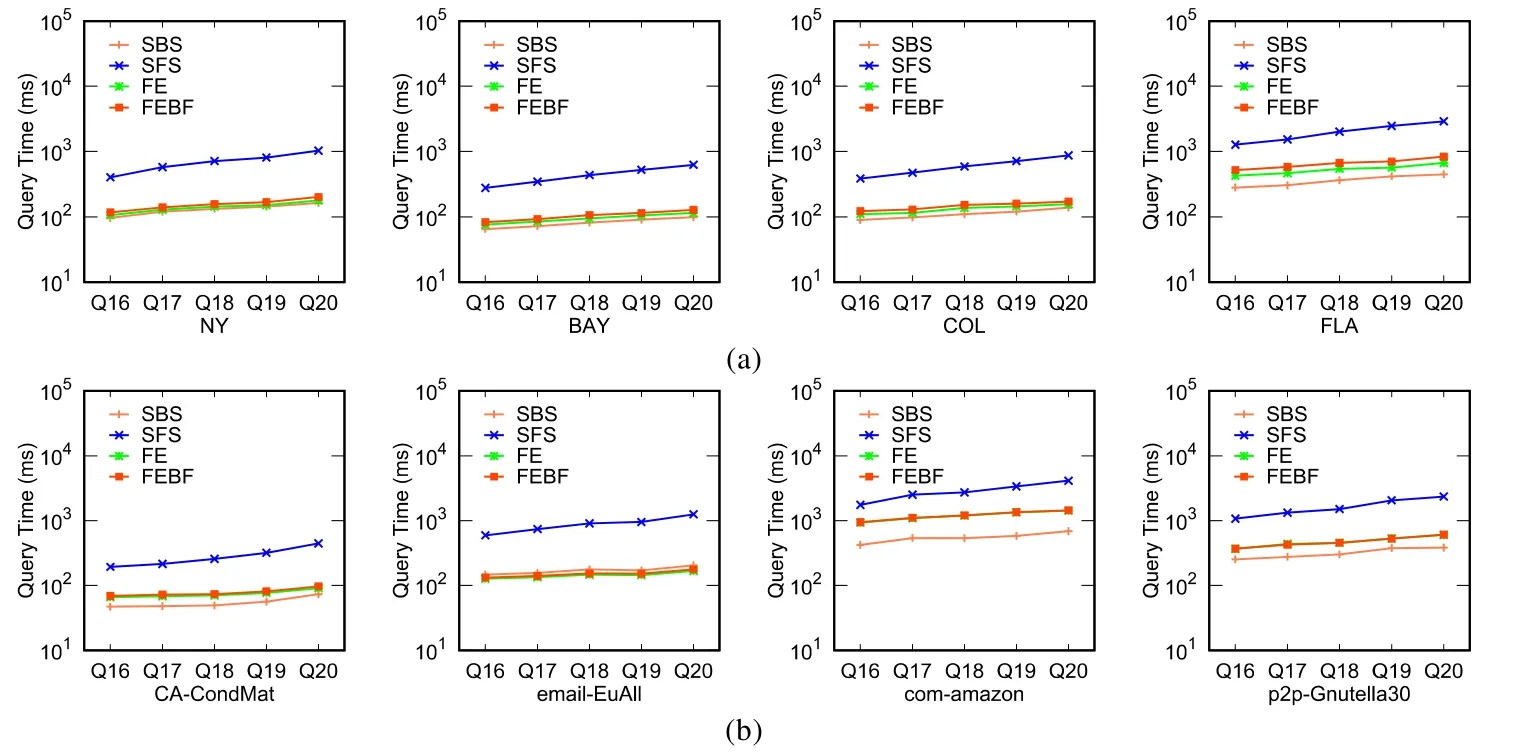
Fig.7 Query efficiency on Q16～Q20圖7 在Q16～Q20上的查詢效率

查詢集Q21～Q25對應的規則R規模較大,因此算法的運行時間較長.在此,本文僅給出算法FEBF的查詢時間.從圖8的結果來看:即使在規則R的規模較大時,本文的FEBF算法也可以在一定時間內給出問題的解.

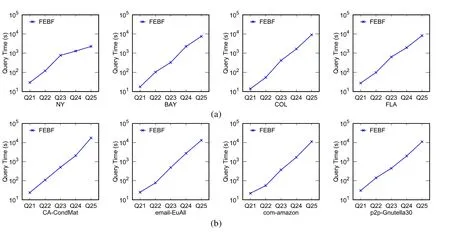
Fig.8 Query efficiency on Q21～Q25圖8 在Q21～Q25上的查詢效率

· 改進后的算法有效性

FEBF算法是FE算法的改進算法,圖9展示了FE和FEBF算法在查詢集Q11～Q15上的加速比(加速比是指FE算法的查詢時間與FEBF算法的查詢時間的比值),結果表明:在每個數據集上,隨著規則點個數的增多,加速比越來越大.顯然,改進后的FEBF算法的運行效率極大地優于FE算法的運行效率.

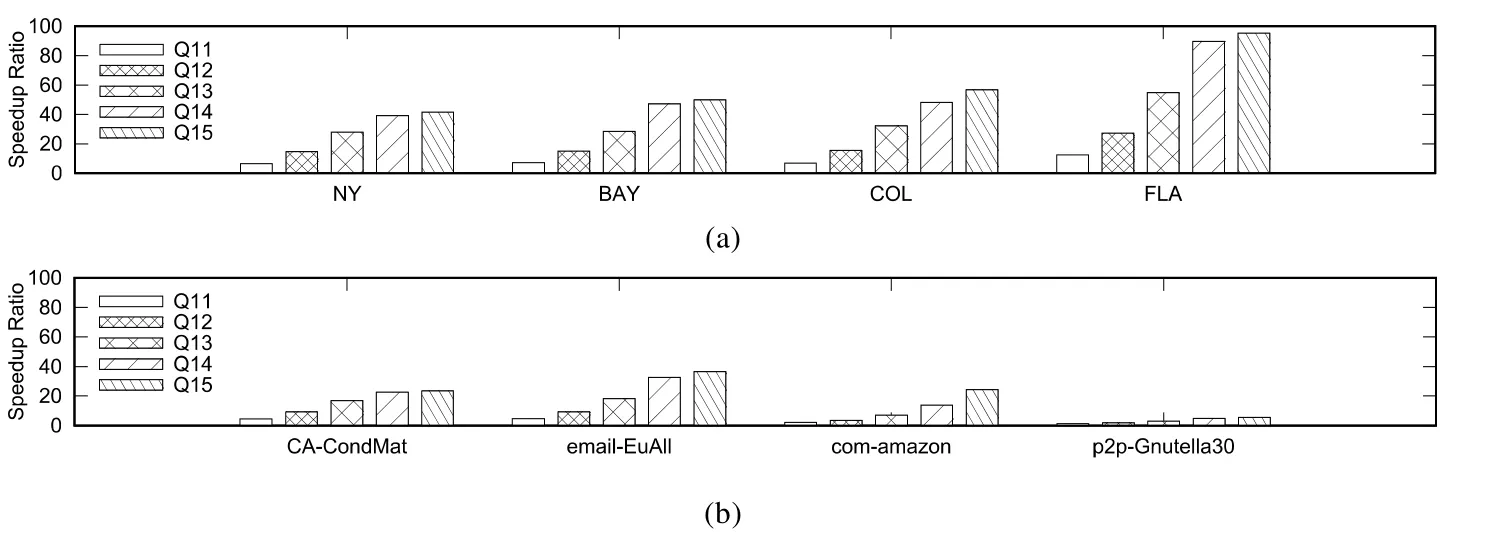
Fig.9 Speedup ratio of improved algorithm圖9 改進后算法的加速比

FE和FEBF算法的查詢時間主要與生成的子排列個數有關:生成的子排列越多,查詢時間則越長;反之,查詢時間則越短.因此,本文用子排列的減少比(NFE表示FE算法生成的子排列個數,NFEBF表示FEBF算法生成的子排列個數)來反映FE和FEBF算法的性能優劣,結果如圖10所示.對于道路交通網數據集,FEBF算法生成的子排列個數比FE算法生成的子排列個數降低了至少20%;對于非道路交通網數據集,FEBF算法生成的子排列個數相比于FE算法生成的子排列個數也有所降低.

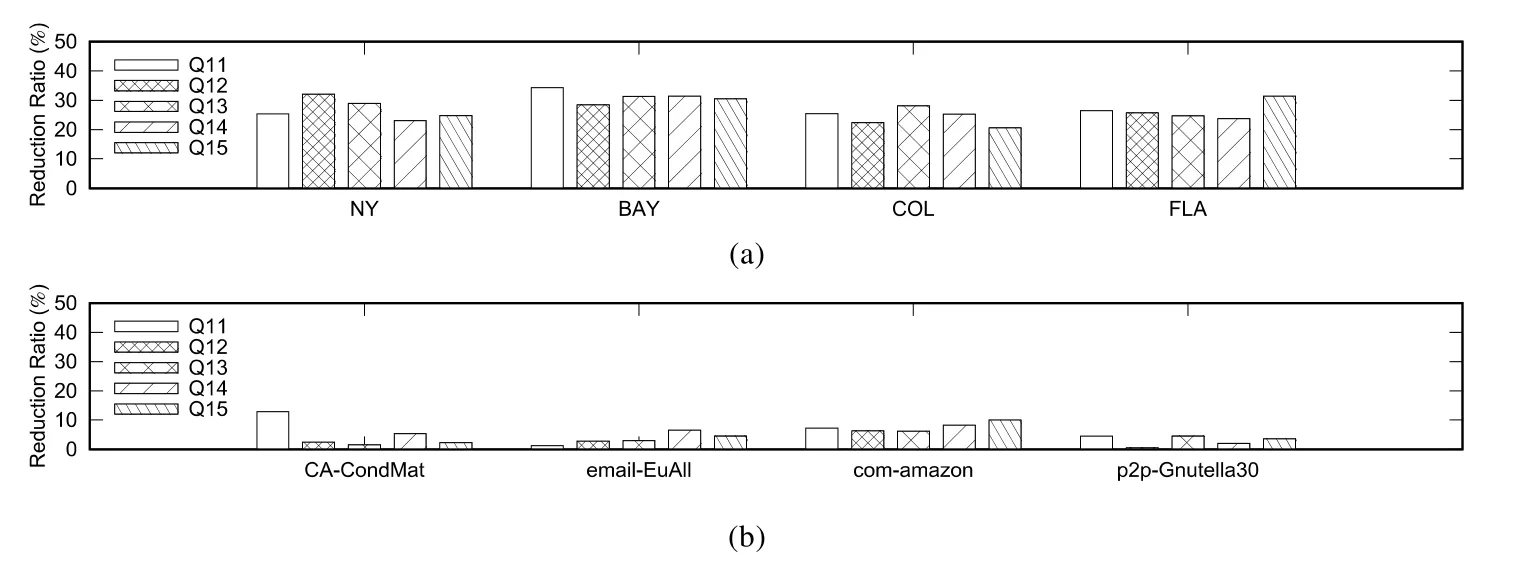
Fig.10 Reduction ratio of sub-permutation圖10 子排列的減少比

· 優化技術的有效性

對于FEBF算法,本文提出了3個優化技術.圖11展示了在查詢集Q11～Q15上,FEBF算法在未使用優化技術與使用優化技術兩種情況下的加速比(即未使用優化技術的FEBF算法的查詢時間與使用優化技術的FEBF算法的查詢時間的比值),結果表明:在每個數據集上,相對于未使用優化技術的 FEBF算法,使用優化技術的FEBF算法能夠有效降低算法的查詢時間.

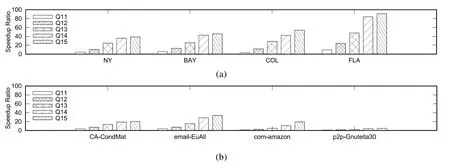
Fig.11 Effectiveness of optimizing techniques圖11 優化技術的有效性

7 相關工作

本節介紹相關的工作,并把最短路徑問題分為傳統的最短路徑問題和 ORQ問題.ORQ問題又細分為如下幾類:已指定必須經過類別的訪問順序、未指定必須經過類別的訪問順序、部分指定必須經過類別的訪問順序.下面分類依次介紹相關的工作.

· 傳統的最短路徑問題

傳統的最短路徑問題具有不同的應用場景.稠密距離圖(dense distance graph,簡稱 DDG)是平面圖的分解圖,即:將一個平面圖分解為幾個區域,每個區域所包含的頂點個數最多為r,其中,r

· 已指定必須經過類別的訪問順序

已知必須經過的類別集合,若已規定所有類別的訪問順序,則 ORQ問題稱為類別全序的最優路徑查詢問題.R-LORD[23]是一個精確算法,用來求解空間數據集上類別全序的最優路徑查詢問題,假設p*=(vs,v1,v2,…,vr,ve)是上述問題的一個最優路徑,則p*的任意一個后綴p在p中都是最短的,P是滿足下面兩個條件的路徑集合:(1) 以p的起點作為起點;(2) 與p相同的順序訪問p中的所有類.基于此,R-LORD采用動態規劃的方式逐步構建最優后綴表.在構建最優后綴表之前,R-LORD利用貪心算法得到一條滿足類別訪問順序的路徑,并用此路徑的權重作為閾值來過濾不可能成為最優路徑的后綴.在構建最優后綴表時,R-LORD利用橢圓剪枝技術來排除無法構成最優路徑的子路徑.Michael等人提出了基于動態規劃的算法求解類別全序的最優路徑查詢問題[24],此算法主要是逐步構建一個實值矩陣X,X是一個r行g列的矩陣,其中,r表示必須經過的類別個數,g表示規模最大的類中包含的頂點個數.矩陣的每個元素X[i,j]是一個最優子路徑的長度,此路徑表示從起點到訪問順序為i的類別中的第j個頂點的最優子路徑.此外,Michael還設計了兩個優化技術,分別為圖結構優化和問題結構優化,并通過剪枝策略來解決由于類別規模過大導致算法運行時間過長的問題.由于本文所研究的問題對類別的訪問順序只做了部分的限制,即,并未完全指定每個類別的訪問順序,因此,上述兩個算法都無法用來求解本文所研究的問題.

· 未指定必須經過類別的訪問順序

已知必須經過的類別集合,若沒有規定任何類別的訪問順序,則ORQ問題稱為類別無序的最優路徑查詢問題.對于空間數據集,Li等人提出了幾個近似算法來求解類別無序的最優路徑查詢問題[25].ANN[25]是一個近似算法,其主要思想是:從單個起點構成的路徑p′開始,反復地從G中選擇一個離p′末尾頂點最近的點(記為vc),且vc對應的類別c尚未被p′訪問,然后將vc添加到p′的末尾構成新的p′.重復上述操作,直至所有的類別都已被p′訪問,最后將終點添加到p′的末尾,從而構成一條包含指定所有類別的路徑.AMD[25]也是一個近似算法,它的主要思想是:對于每一個必須訪問的類c,從類c中選擇一個頂點vc,使得vc離起點和終點的距離之和小于其他任意點離起點和終點的距離之和,從每個類中選擇得到的點構成集合VC,然后調用ANN算法(此處在調用ANN算法時,將G中的點替換為VC中的點),從而得到一條包含指定所有類別的路徑.LESS[26]是一個求解此類問題的精確算法,它的本質是將指定的所有類別進行全排列,每個類別在排列中的位置表示此類別在路徑中被訪問時所處的位置.對于每一個排列,按順序依次從排列的類別中選擇一個頂點,最終構成一條包含指定所有類別的路徑.LESS枚舉出所有排列對應的所有路徑,然后選擇一條長度最小的路徑作為問題的最優解.由于本文所研究的問題對類別的訪問順序做了部分的限制,而上述算法只能解決訪問順序沒有限制的情況,因此,上述兩個算法都無法用來求解本文所研究的問題.

· 部分指定必須經過類別的訪問順序

已知必須經過的類別集合,若已規定部分類別的訪問順序,則 ORQ問題稱為類別偏序的最優路徑查詢問題.NN[14]是求解類別偏序的最優路徑查詢問題的啟發式算法,它最終返回一條接近最優的路線,算法的具體流程為:從單個起點構成的路徑p′開始,反復地從G中選擇一個離p′末尾頂點最近的點(記為vc),且vc對應的類別c在圖GQ(GQ是查詢圖且是一個有向無環圖,GQ中的每個點都對應于G中的一個類別信息,GQ中每條有向邊(c,c′)表示G中類別c的點先于類別c′的點訪問)中且入度為0,然后,從GQ中刪除類別c以及與它相連的邊,接著將vc添加到p′的末尾構成新的p′.重復上述操作,直至GQ中不包含任何點,最終找到一條滿足約束條件的路線.Li等人提出了4個精確算法來求解在空間數據集上的此類問題[13],它們分別為SBS,BBS,SFS和BFS. SBS利用R-LORD[23]中提出的后綴最優定理,逐步求解1后綴到r后綴(r為必須經過的類別的個數),然后,從r后綴中選擇一個路徑長度最小的路徑作為此問題的最優解.BBS是 SBS的優化算法,對于每一個必須經過的類別,BBS首先將具有相同類別的點進行聚類,即,把彼此距離較近的一些點歸為同一組,然后,BBS以每一個組的點為單位,執行與SBS相同的操作,當每個類中包含的點的個數較多時,BBS可以很大程度地提高算法的運行效率.SFS本質上是采用分層回溯的方式求解問題的解,算法運行時所處的層數表示此時已得到的子路徑所包含的類別個數.SFS采用 NN[14]添加頂點的方式,每次選擇離當前路徑末尾頂點最近的一個點,每往路徑中添加一個新的頂點,則意味著SFS進入到當前層的下一層,然后再執行相同的添加頂點的操作.當算法到達第r層后,則表明此算法已找到一條滿足約束的路徑,然后算法回溯到r-1層,將離當前路徑末尾頂點次近的點添加到路徑的末尾.重復上述回溯操作,直至得到所有滿足約束的路徑,最后返回一條最優的路徑.BFS是 SFS的優化算法,與BBS類似,BFS首先將具有相同類別的點進行聚類,即,把彼此距離較近的一些點歸為同一組,然后,BFS以每一個組的點為單位,執行與SFS相同的操作,最終得到問題的最優解.由于本文所研究的問題是基于普通的圖數據而非空間數據,因此上述 4個算法無法直接應用于本文所研究的問題,而且這些算法較少過濾掉不可能成為最優路徑的子路徑,使得算法的運行時間較長.

廣義旅行商問題是傳統旅行商問題的變種,帶優先級約束的旅行商問題屬于廣義旅行商問題的一種,它可以描述為:已知n個城市之間的相互距離,現有一旅行商計劃全部訪問這n個城市,并且每個城市只能訪問一次,在訪問這些城市時必須滿足一定的約束條件(例如,必須先訪問城市1和城市2,然后才能訪問城市3),最后,旅行商返回到出發的城市,目的是尋找一條旅行商行走的路線,使得此路線滿足上述約束條件且具有最小的距離.Ascheuer等人[27]提出了基于分支切割的算法來解決不對稱的有約束條件的旅行商問題.Moon等人[28]和Wang等人[29]分別采用遺傳算法和整數規劃的方式解決帶有約束條件的旅行商問題;有優先約束的哈密頓路徑問題(Hamiltonian path problems with precedence constraints)又稱為順序排序問題(sequential ordering problem),可描述為尋找由指定的起點前往指定的終點的最短路徑查詢問題,途中經過其他所有頂點有且只有一次,而且頂點之間存在先后順序約束,Karan等人[30]提出了一個基于分支界限法的算法來解決順序排序問題.已有的解決廣義旅行商問題的精確算法本質上為枚舉出每一種可能的路徑,因此這些算法不適用于大規模圖上問題的求解,而本文所提的算法可以很好地應用于大規模圖上的查詢.

8 總 結

本文設計了一個基于最優子路徑的前向擴展算法,該算法可以快速求解基于規則的最短路徑查詢問題,并設計了前向擴展算法的改進算法——基于最短優先策略的前向擴展算法.從實驗的結果來看,基于最短優先策略的前向擴展算法對原始算法的查詢效率有很大程度的提高.本文在真實的數據集上設計了大量的實驗,并與已有的性能最好的算法作比較,實驗結果表明,本文的算法大幅度優于已有的算法.