改進的ABE在公有云存儲訪問控制中的研究*

許 萌，鮑安平，呂湛山

1.南京信息職業技術學院，南京 210023

2.山西晉煤華昱煤化工有限責任公司，山西 晉城 048000

1 引言

隨著計算機網絡以及軟硬件技術的蓬勃發展，云存儲技術以及相關應用正處于快速成長的階段[1]。這使得數字資源的在線傳播變得愈加便捷，人們只要通過手機等無線設備就可以輕松地獲取各類數字資源。然而考慮到云端設備是大多為第三方擁有，通過云端來分享數字資源有可能會威脅到數據擁有者的隱私。因此針對云存儲建立敏感數據隱私保護機制就變得至關重要。不僅如此，任何云存儲平臺涉及到海量用戶的活躍參與，因此急需一套細粒度的訪問控制機制來設置海量用戶的訪問權限。

屬性基加密算法[2-3]（attribute-based encryption，ABE）是一種具有相當應用前景的技術，它不僅能夠保證數據存儲的安全性，還能夠實現靈活的訪問權限設置。基于屬性的密碼體制目前包含兩大類經典的算法，一類是基于密文策略的屬性加密算法[4-5]（ciphertext-policy ABE，CP-ABE），該算法將訪問策略嵌入到密文當中，而用戶的私鑰則綁定了一個用來表示用戶身份的屬性集合。另一類是基于密鑰策略的屬性加密算法[6-7]（key-policy ABE，KP-ABE），該算法將訪問策略嵌入至用戶的私鑰，而密文則與一個屬性集合相關。當屬性集合與訪問策略足夠接近并完成匹配的話，用戶就能夠成功獲取數據的明文。相比傳統公鑰加密算法，ABE最大的特點在于它具有一種模糊性質，即能夠實現加密數據的多對多分享。因此以上性質使得ABE能夠為公有云上的數據存儲與分享提供既安全又靈活的訪問控制。

1.1 相關研究

Sahai和Waters[3]首次提出了一種模糊的基于身份加密算法（fuzzy identity-based encryption，FIBE）。FIBE采用一種描述性的屬性集合來定義身份，該算法為ABE算法的提出開創了先河。Goyal等人[6]在FIBE的基礎上首次提出了一種KP-ABE算法，將訪問策略嵌入到密鑰當中，而屬性集合則嵌入到密文當中，該算法結構簡單但是功能有限，并不適合在公有云環境中應用。Bethencourt等人[4]受到啟發，有針對性地提出了一種CP-ABE算法，使得加密者能夠自由制定訪問策略，為ABE算法在數據存儲與訪問控制領域的應用奠定了基礎。文獻[8]提出了一種基于多鑒權中心的ABE算法，每個健全獨立擁有各自的主密鑰并且管理不同的屬性，這使得單個健全中心不再具有獨立獲取明文的能力。Hur[9]指出多個鑒權中心共同產生非常龐大的互動開銷，提出由健全中心和數據存儲中心協作產生主密鑰，并提出了一種間接撤銷方式，在提高了計算效率的同時也豐富了ABE的功能。文獻[7]提出了一種在標準模型下實現完全安全性的KP-ABE方案，同時計算效率與選擇性安全模型下的方案相當。文獻[10]采用零知識證明使兩個鑒權中心互動產生主密鑰從而有效防止密鑰托管問題的產生，同時支持密鑰追責，用戶不可以輕易地將自己的私鑰交由他人使用。文獻[5]提出了一種支持直接撤銷的CP-ABE方案，鑒權中心通過維護一個撤銷列表實現細粒度的快速撤銷，同時其密文、私鑰和公鑰的長度都有所優化，整體效率在一定程度上有所提高。Karati等人[11]考慮到雙線性配對是影響ABE計算效率的主要因素，提出了一種不需要雙線性配對的ABE算法，但是該算法采用閾值門作為訪問策略，因此算法在整體顯得不夠靈活。文獻[12]針對托管、濫用等密鑰管理難題，提出了一種分布式的密鑰管理協議，同時采用一種外包解密的思想使得解密者不需進行任何雙線性配對就可以獲取明文，但是算法整體的計算負載仍然非常大。

1.2 研究動機

盡管國內外學者對ABE算法進行了眾多的研究，但是在公有云的數據存儲與訪問控制領域，ABE距離實際應用還存在兩個亟待解決的問題：

（1）從安全角度考慮，最主要的問題在于現有方案當中的鑒權中心必須是完全可信的機構，因為鑒權中心負責生成全部的公鑰和私鑰。這就意味著鑒權中心可以在用戶不知情的情況下，可以利用主密鑰獨立自主地生成私鑰，進而嘗試解密截取的密文。這個 問題 被稱 為密 鑰托 管 問題[8-10，13]（key escrow problem），是ABE與生俱來的安全性難題。

（2）從計算復雜度考慮，ABE在加解密計算過程中涉及大量的雙線性配對，而雙線性配對本身就需要消耗很大的計算資源[11,14]。在個人電腦乃至大型服務器端，這樣的計算消耗尚可以接受。但在移動云計算逐漸普及的今天，即使軟硬件技術得到極大的發展，移動端的電力和計算資源仍然是非常珍貴的[15]。因此在這樣的情況下，如果將現有的方案直接應用于移動端，那么對優化用戶使用體驗來說將是一次巨大的考驗。

針對以上問題，本文基于KP-ABE改進了ABE算法，改進如下：一方面在鑒權中心無法獨立生成私鑰，即使其安全等級下降為半可信，算法仍然能夠提供安全的密鑰管理；另一方面，改進的算法在加解密過程中不需要進行任何的雙線性配對，相比現有的ABE算法具備更高的計算效率，更適合在移動端構建輕量級的加密與訪問控制方案。最后的規約證明表明，本文方案在隨機預言機模型下能夠抵抗選擇密文攻擊。

2 模型架構

本文算法應用在云存儲訪問控制當中的模型架構如圖1所示。模型當中包含四類主要角色：

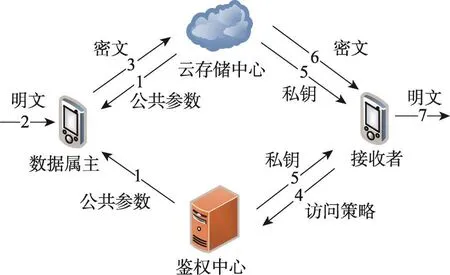
Fig.1 Architecture of model圖1 模型架構

（1）數據屬主：該角色擁有對數據的所有權，并試圖通過移動設備將數據上傳至云平臺，并向指定的群體分享該數據，同時不希望被該群體之外的人獲取該數據。

（2）鑒權中心：該角色在框架內是唯一的，負責密鑰的生成與發布并使之用于訪問權限的控制。

（3）云存儲中心：該角色負責存儲和管理經過加密的數據，同時在本文算法當中也將承擔一部分的密鑰生成與發布工作。

（4）接收者：該角色試圖通過移動設備訪問云存儲中心，并獲取云存儲中心當中的數據。

本文算法將通過以上四類角色的互動來實現云存儲平臺上數字資源的訪問控制。在平臺啟動時，鑒權中心以及云存儲中心基于密碼學原理并結合系統中的全局屬性生成一套公共參數，并向全網的數據屬主廣播該公共參數。每個接收者在平臺中注冊時將獲得自己的訪問策略，由鑒權中心和云存儲中心經過協商分布式地生成接收者的私鑰。數據屬主通過云存儲平臺分享數字資源之前，首先根據自己的屬性集合并結合公共參數對數據進行加密操作，然后將密文上傳至云存儲中心。當某個接收者嘗試下載數字資源時，他將利用自己的私鑰試圖解密密文，若其訪問策略與密文中的屬性集合相匹配，那么則可以順利解密得到數字資源的明文，反之則無法解密從而獲取不到關于數字資源的任何信息。

3 算法設計

本文算法通過四個子算法實現數據屬主、鑒權中心、云存儲中心以及接收者之間的互動，最終實現云存儲的安全訪問控制，具體如下：

3.1 初始化算法

受文獻[12]啟發，在本文提出的改進方案中，初始化算法由密鑰中心和云存儲中心共同執行。首先定義全局屬性空間為 Ω={θ1,θ2,…,θn}。設G 和GT是兩個階為大素數q的加法循環群，P為群G的一個生成元。定義一個哈希函數為H:G→Zq。算法首先輸入一個安全參數k，然后由密鑰中心生成一組唯一的、與全局屬性空間相對應的整數參數{t1,t2,…,tn}∈Zq。對于全局屬性空間中的任意一個屬性θx∈Ω，計算Tx=txP。同時，云服務中心選擇一個唯一的元素y∈Zq并計算Y=yP。最終，初始化算法輸出基本公共參數：

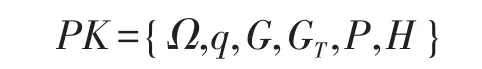
密鑰中心保留自己的主密鑰：

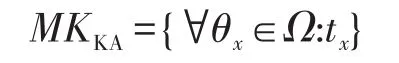
然后輸出自己的公共參數：

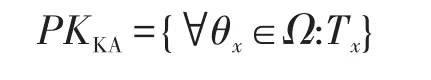
與此同時，與服務中心保留自己的主密鑰：

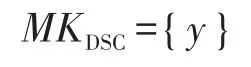
然后輸出自己的公開鑰：

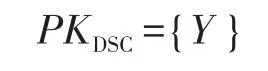
最終初始化算法輸出公共參數為：

3.2 密鑰生成算法

為了防止密鑰托管，有些學者提出了多鑒權中心的方案[16-17]。本文算法不打算增加任何實體，而是利用鑒權中心和云存儲中心的協作共同生成密鑰。算法輸入為鑒權中心和云存儲中心的主密鑰MKKA和MKDSC以及公共參數params。當接收者發出私鑰生成請求時，他需要提交一個訪問策略T。對于訪問策略T，其中任意一個葉節點均表示某一個屬性，而其余所有的非葉節點均為閾值門。對于任意一個節點x，均有一個索引值index(x)與之相對應，如果該節點是非葉節點，如果它的子節點個數是mx，那么該節點的閾值為kx(1≤kx≤mx)，相應的閾值門為(kx,mx)；如果該節點是葉節點，則該節點的閾值門為(1,1)。隨后鑒權中心與云存儲中心通過以下步驟共同生成數據訪問者的私鑰：

（1）云存儲中心生成一個隨機數r∈Z*q，計算A=ry并將其發送給鑒權中心。

（2）為了不失一般性，假設訪問策略T的根節點為root，其閾值為kroot。當鑒權中心獲得參數A后，為訪問策略的根節點生成一個隨機多項式qroot(X)，該多項式滿足以下兩個條件:

①多項式的次數為droot=kroot-1；

②多項式常數項等于參數A，即qroot(0)=A。

（3）對于任意節點的子節點x，設其閾值為kx，鑒權中心同樣生成一個對應的隨機多項式，該多項式滿足以下兩個條件：

①多項式的次數為dx=kx-1；

②多項式常數項為qx(0)=qparent(x)(index(x))，其中函數parent(x)返回x的父節點。

（4）對于訪問策略中的任意屬性θx，鑒權中心發送Dx=qx(0)+tx給接收者。

（5）云存儲中心發送D=r給接收者。

最終，數據訪問者獲得關于訪問策略T的私鑰為：

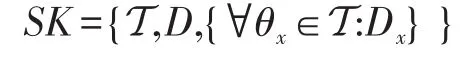
3.3 加密算法

該算法由數據屬主執行，算法輸入為公共參數params、數據屬主的屬性集合S和待分享數據的明文m。首先選擇一個秘密參數s∈Zq，然后執行如下計算：

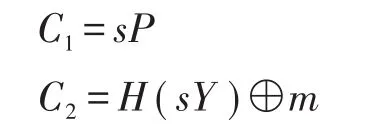
對于屬性集合中的任意屬性θx∈S，計算：

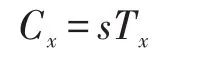
最終算法輸出密文：

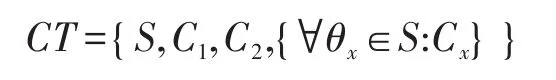
3.4 解密算法

該算法由接收者執行，算法輸入為公共參數params、待分享數據的密文CT和接收者的私鑰SK。在說明算法執行步驟前首先引入關于拉格朗日插值的概念，假設對于一個元素有限的數值集合S={a1,a2,…}，關于其中任意一個元素i的拉格朗日插值表示為：

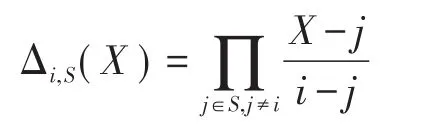
其次定義兩個函數：

Λ(x)：對于訪問策略中的任意一個節點x，返回x所擁有的全部子節點。

Λ′(x)：對于訪問策略中的任意一個節點x，返回x所擁有的全部子節點的索引值。

對于訪問策略中的任意節點x，解密算法將執行一個函數DecryptNode(x)，該函數的執行過程如下：

若x是葉節點，則計算：

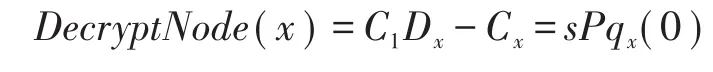
若x是非葉節點，記x的任意子節點z經過該函數計算過后得到的結果為Fz，那么該函數對于x的計算為：

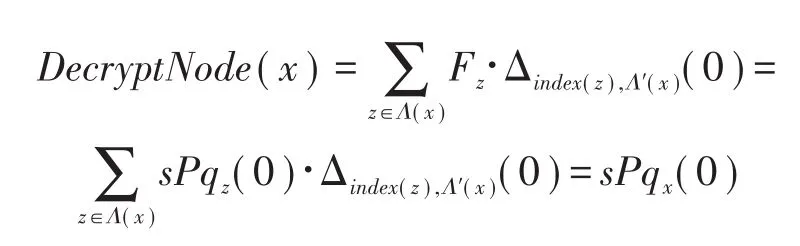
經過以上函數的迭代計算得到：

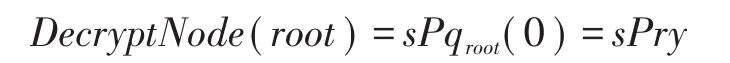
最終通過以下計算得到明文：

4 算法分析

4.1 機密性

算法將因子H(sY)嵌入到了密文當中，該秘密隱藏了云存儲中心的主密鑰MKDSC=。如果接收者私鑰的訪問策略與密文的屬性集合不相匹配的話，接收者永遠不可能恢復出云存儲中心的主密鑰。反之接收者則可以很快恢復出云存儲中心的主密鑰，進而得到因子H(sY)并抽取出正確的明文。

在任意不同的兩種明文的加密過程中，由于加密算法在因子H(sY)中還嵌入了不同的秘密隨機數s，即使接收者每次都能正確執行解密操作，他也只能獲得與當前密文相關的秘密。也就是說，每一個因子H(sY)只與當前的密文相關，接收者無法通過之前獲得的因子去解密其他的密文，因此保證了密文與密文之間的安全隔離，彼此不互相干涉機密性。

4.2 抗合謀攻擊

合謀攻擊是一種針對密碼系統的經典攻擊方式。合謀攻擊指的是若干個攻擊者通過溝通協商，將各自持有的私鑰組件進行拼接組合，非法地生成一個全新的私鑰。這個全新的私鑰擁有更強大的解密能力，能夠解密那些利用私鑰組件無法單獨解密的密文。

在私鑰生成階段，云存儲中心每生成一個全新的私鑰之前都會產生一個獨特的隨機數r。云存儲中心將這個隨機數與其主密鑰MKDSC=相乘得到因子ry，并通過訪問樹將因子ry分享給訪問策略中的各個屬性。由于不同接收者的訪問策略里包含了不同的秘密，因此接收者彼此之間即使通過溝通協商將各自的私鑰組合起來獲得一個全新的私鑰，這個看似能夠與更多屬性集合匹配的全新私鑰仍然無法恢復出一個正確的因子ry。因此本文算法在云存儲訪問控制模型當中能夠很好地規避合謀攻擊帶來的潛在隱患。

4.3 抗密鑰托管

本文算法利用鑒權中心與云存儲中心的協作實現私鑰的分布式生成。在私鑰生成階段，云存儲中心產生一個隨機數r并與其主密鑰相乘獲得待分享的因子ry，緊接著將因子ry發送給鑒權中心。隨后鑒權中心負責生成相應的接收者私鑰。

對于云存儲中心來說，它不能知道鑒權中心的主密鑰MKKA={?θx∈Ω:tx}，從而無法恢復出私鑰當中的組件{?θx∈T:Dx}。而對于鑒權中心來說，它不知道云存儲中心的主密鑰MKDSC=以及云存儲中心產生的隨機數r，從而無法恢復出私鑰當中的組件D=r。也就是說，鑒權中心根本不能從已知的因子ry里獲得關于因子H(sY)的任何信息。綜上所述，盡管鑒權中心和云存儲中心共同參與了接收者私鑰的生成，但是都無法獲取私鑰的完整組件。因此，本文算法展現出來的分布式密鑰生成機制足以克服密鑰托管問題。

為了說明本文方案在抗密鑰托管方面進行改進的效果，將本文算法與其他類似的抗托管算法進行了對比，對比結果如表1所示。在這里定義一方將一組數據發送給另一方為1次交互。在表1當中列出了現有的克服密鑰托管的方案，在生成私鑰時所需的交互次數總數。改進的ABE算法具備分布式的密鑰生成機制，其所需的交互次數為1次。文獻[8]為了克服密鑰托管問題，采用了多鑒權中心的方法，每個鑒權中心負責生成關于一部分屬性的密鑰組件。在生成私鑰的過程中由于每兩個鑒權中心之間需要完成一些交互，因此當鑒權中心個數為n，總體上生成私鑰所需的交互次數復雜度為O(n2)。文獻[13]為了克服這種復雜度攀升的問題只采用了兩個鑒權中心，而兩個鑒權中心只需要進行一次交互即可實現私鑰的發布。文獻[9]進一步將鑒權中心的部分功能轉移至云存儲中心上去，在不需要增加任何實體的情況下需要3次交互就可以有效克服密鑰托管問題。文獻[12]在此基礎上通過更多的交互實現了私鑰的分布式管理，每次生成私鑰需要進行8次交互。因此本文方案在抗密鑰托管的同時，將生成私鑰所需的交互次數降低到僅1次，相比表1中其他方案是最高效的。另外，本文方案所采用的模型只需要一個鑒權中心，利用該鑒權中心與云存儲中心進行交互即可，不需要增加額外的鑒權中心來承擔密鑰管理工作，因此在模型復雜度上盡可能做到了簡潔。綜上所述，本文方案的抗密鑰托管功能是比較高效、簡潔的。

Table 1 Comparison of different escrow-free mechanisms表1 不同抗托管機制的對比

4.4 計算效率

為了分析本文算法經過改進后的計算性能，將本文算法與文獻[4-7,18]中的算法進行了對比。為便于分析比較，如表2所示，首先定義了若干變量。

Table 2 Definitions of some variables表2 若干變量的定義

其次，從密鑰尺寸、密文尺寸以及加解密過程中所需的雙線性配對次數三方面對本文算法以及其他類似算法進行了分析。結果如表3所示，文獻[4]設計了一種基于密文策略的屬性加密方案，由于支持數據屬主直接定義訪問策略，導致接收者私鑰尺寸過大，同時接收者必須執行大量的雙線性配對才能獲取消息明文。文獻[5]提出了一種支持用戶直接撤銷的ABE方案，將接收者的身份信息植入到其私鑰當中，同時由鑒權中心維護一個撤銷用戶的列表，在執行加密算法時將列表植入到密文當中。可以看出，文獻[5]的方案相比其余方案并不算大，但是在密文當中植入了撤銷列表，并為每個撤銷用戶配置了1個位于循環群G上的唯一元素，而且在解密時需要額外執行2Nr次雙線性配對。文獻[6]最早提出了KPABE算法，其密鑰尺寸、密文尺寸以及雙線性配對次數都非常小，計算效率高，但是考慮到只實現了KPABE算法的核心功能，其計算和存儲代價仍然不理想。文獻[7]提出的是一種在標準模型下完全安全的ABE算法，該算法建立在合數循環群上，而其他方案都是建立在素數群上，但是可以看出該方案在提高了系統的安全性的同時保持了與文獻[4]方案相當的計算效率，無論是密鑰尺寸、密文長度還是解密時需要執行的雙線性配對數量，都與文獻[4]方案基本相當。文獻[18]為了增強訪問策略的表達性，采用了屬性矩陣來構成屬性之間的等級關系，其中屬性矩陣的行數L代表了等級總數，但是這也導致了接收者不得不執行大量的雙線性配對來獲取消息明文。

Table 3 Performance comparison表3 性能對比

在本文所提出的改進ABE方案中，密鑰尺寸與文獻[6]方案相比只多出一個，在假設訪問策略與屬性集合所包含屬性的平均數目相當的情況下，本文所提出的方案在密鑰尺寸上幾乎是文獻[4]和文獻[7]方案的50%。同時，本文改進的ABE算法在密文尺寸上與文獻[4]和文獻[18]所提方案相同，都是(2Nas+2)幾乎是文獻[6]和文獻[7]方案的2倍。然而，本文方案在加解密過程中不需要執行任何的雙線性配對，極大地降低了計算開銷，這是其他方案都不具備的性質。因此，文本改進的方案在效果上對于移動端的數據屬主和接收者更為友好，更適合于在移動云計算環境下部署的相關應用，例如通過手機端進行私人健康數據、企業內部文件以及社交媒體數據的安全存儲與分享。總之，不論是數據屬主還是接收者，只需要在移動端執行少量的加解密計算即可以實現數據在公有云上的存儲、分享等操作。

5 安全性證明

5.1 困難假設

對于本文所設計的方案，其安全性是構建在計算性Diffie-Hellman問題[19]（computational Diffie-Hellman problem，CDH）的困難性基礎之上的。

定義（計算性Diffie-Hellman困難假設）已知一個階為素數q的加法循環群G，設P是群G的一個生成元。那么，已知群G中的兩個元素P1=aP和P2=bP，其中a,b∈Zq，不存在一個概率性的算法能夠在多項式時間內計算出P3=abP。

5.2 證明過程

基于給出的困難假設，給出如下的定理：

定理如果計算性Diffie-Hellman問題是困難的，那么本文設計的方案在隨機預言機模型下能夠抵抗選擇明文攻擊。

證明為了給出定理證明，沿用了文獻[20]中的證明思路設計了如下的挑戰游戲：

（1）初始化階段

定義一個階為素數q的加法循環群G，P為群G的一個生成元。挑戰者C選擇兩個隨機數a,b∈Zq，然后將P、P1=aP和P2=bP發送給模擬器B。

（2）詢問階段

本階段敵手將向模擬器發起以下三種詢問并試圖從中獲取信息：

①公共參數詢問：模擬器B定義一個隨機預言機H:G→Zq，將參數發送給敵手A，同時生成一個列表List1={θx,tx,c,Tx}。當A發送關于屬性θx的公共參數詢問時，B開始掃描整個列表。如果θx存在于列表當中，那么返回該屬性對應的Tx；如果θx不存在，那么B選擇一個比特參數c∈{0,1}，使其取值的概率分布滿足Pr[c=0]=δ，Pr[c=1]=1-δ，其中θ是介于0到1之間的隨機數。當c=0時返回Tx=txP，否則Tx=txP1，最終模擬器B把該屬性的參數添加到List1里。

②私鑰詢問：模擬器生成第二個列表List2={T,D,{Dx}}。當A發送關于訪問策略T的私鑰詢問時，B開始掃描整個列表。如果T中包含列表List1當中的屬性，那么告知A游戲結束并顯示錯誤代碼ERROR1；如果T不包含List1當中任意屬性的話，選擇兩個隨機數r,R∈Z*q并為T的根節點root分配一個隨密結果m=CT⊕H(X)，并將新的{S,CT,X,H(Xm)},添加進List3里。

（3）挑戰階段

敵手A向模擬器B提交兩段長度相同的明文m0和m1，以及一個挑戰屬性集合S*。模擬器隨后檢查挑戰屬性集合中的所有屬性是否都在List1當中。如果存在屬性不在List1中，那么告知A挑戰結束并返回錯誤代碼ERROR4；如果所有屬性都在List1中，那么檢查所有屬性在List1里對應的元素c。若存在c=0，那么告知A挑戰失敗并返回錯誤代碼ERROR5，否則從List3中隨機抽取元素H(X)，選擇一個隨機的比特β∈{0,1}以 及 一 個 隨 機 數 s∈Z*q，隨后開始計算。最終模擬器機多項式qroot，使得droot=kroot-1，同時使得qroot(0)=R。

③解密詢問：模擬器生成第三個列表List3={S,CT,X,H(X),m}。當A發送一個關于屬性集合S的密文并請求解密時，B開始檢查S當中的屬性是否出現在List1中。如果S當中存在屬性不在List1里，那么告知A游戲結束并顯示錯誤代碼ERROR2；否則進一步檢查S當中的屬性在List1當中對應的元素c。如果存在屬性對應的元素c=1，那么告知A游戲結束并顯示錯誤代碼ERROR3；否則生成一個S可滿足的訪問策略T，并生成對應的私鑰。模擬器通過該私鑰計算 X=D-1DecryptNode(root)和H(X)。最終B返回加B返回挑戰密文。敵手A通過密文輸出β′作為對β的猜測。如果β′=β，那么敵手取勝，同時模擬器輸出P′3=s-1X給挑戰者C作為CDH問題的解。

由以上游戲流程可知，當ERROR1、ERROR2、ERROR3不發生時，模擬器返回的所有結果都是有效的，而且與本文的方案在真實環境中的計算結果無法區分。同時當ERROR4和ERROR5不發生時，模擬器才有可能借助敵手的結果給出CDH難題的正確解。記以上游戲過程中公共參數詢問的次數為q1，私鑰詢問的次數為q2，解密詢問的次數為q3。設全局屬性空間大小為每一個訪問策略里包含的屬性平均個數為u。根據以上參數可以得到ERROR1到ER ROR5不發生的概率。這些事件的概率如表4所示。

Table 4 Occurrence probabilities of all events in challenge game表4 挑戰游戲中所有事件發生的概率

根據表4中各個事件的概率可得，模擬器給出CDH問題正確解的優勢ε′為：

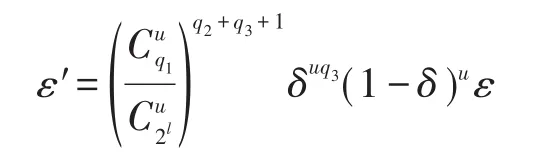
因此若存在多項式時間的算法能夠以不可忽略的優勢給出CDH問題的正確解，那么一定存在多項式時間的敵手能夠以不可忽略的優勢破解本文的方案。而正因為CDH問題是難解的，那么可以證明，本文方案是安全的。

6 結束語

針對現有ABE方案的不足，基于KP-ABE改進了現有的ABE算法，設計了一種高效的抗托管云存儲訪問控制模型，該模型在不增加任何實體的情況下能夠分布式地生成接收者私鑰，解決了ABE算法中的密鑰托管問題。由于加解密過程中不需要進行任何雙線性配對，該模型能夠保證較高的計算效率。最后通過規約證明本文方案在隨機預言機模型下能夠抵抗選擇密文攻擊。提出的算法在安全性以及算法效率兩方面對現有的ABE算法進行了改進，適合個人醫療電子數據管理系統、大型企業信息管理系統、網絡云盤等基于公有云的應用場景。相比現有的ABE算法，更適合在移動端構建輕量級的加密與訪問控制方案。

此外，提出的算法在密文長度上仍然保持著較長的尺寸，某種程度上可以認為是以存儲為代價換取了計算效率的提升。同時算法僅僅在普適的公有云環境下構建，尚未針對具體的應用采取優化措施。因此實現進一步縮短密文的尺寸，同時在真實應用場景下進行實際的部署，將是下一步工作考慮的重點。