軟決策分析方法及其在智能推薦中的應用*

陸汝華，張家錄，鐘嘉鳴

1.湘南學院 軟件與通信工程學院，湖南 郴州 423000

2.湘南學院 數學與金融學院，湖南 郴州 423000

3.湘南學院 經濟與管理學院，湖南 郴州 423000

1 引言

軟集理論是Molodtsov教授建立的一種描述和處理不確定性的數學理論。軟集是由參數集及其到論域的冪集上的一個集值映射構成的二元組，或者說軟集就是論域上由某些參數組織起來的一些子集構成的整體。軟集中每個參數對應的子集稱為近似集，軟集理論中對近似集不做任何限定，近似集可以是空集，而且不同參數對應的近似集的交集可能非空。這使得軟集概念涵蓋的范圍非常廣泛，且具有靈活多變、適于應用的特點[1-2]。基于軟集的決策研究吸引了國內外眾多學者的注意，軟集理論研究也得到快速發展，軟集理論在不確定決策方面的應用也是其最為活躍的研究方向之一。如，Maji教授等人使用軟集描述各個對象關于決策屬性的滿足情況，通過軟集計算來決定決策對象的選擇值，以描述對象的優劣程度，并基于選擇值的大小確定最優決策對象或方案[3-5]。Roy和Maji教授等人研究了模糊軟集，給出了一種通過模糊選擇值排序的決策方法[6-7]。馮等人給出了軟集、粗集和模糊集進行比較，結合定義軟粗集、粗軟集和模糊粗軟集等的相關概念，指出粗集是軟集的一種特殊情況[8-9]，并給出軟集及模糊軟集等在決策、屬性約簡等方面的應用[10-11]。到目前為止，軟集理論已經在分類、預測和模擬等方面得到了一些成功的應用[12-14]，但軟集理論在諸如聚類分析、關聯關系分析、模式識別和近似推理等方面的應用研究，還少有相關文獻報道。

商務推薦是不確定性決策理論應用的方向之一。目前主流的推薦方法包括基于內容的推薦、協同過濾推薦、基于知識推薦和組合推薦四種。各種推薦方法研究的重點主要集中在對象之間的相似性，協同過濾推薦考慮的是用戶之間的相似性，內容推薦中關注的是所推薦商品之間的相似性。目前各種推薦方法常用的相似性計算方法有向量空間相似度、Pearson相關、Spearman相關、夾角余弦方法等[14-16]。從信息論的角度看，A與B之間的相似度一方面與它們的共性相關，共性越多，相似度越高，當A與B完全相同時，相似度達到最大值；另一方面與它們的區別相關，區別越大，相似度越低[17]。電子智能推薦是智能推薦的主要應用方向之一，它是“利用電子商務平臺向用戶提供商品信息和建議，幫助用戶決定應該購買什么產品，模擬銷售人員幫助客戶完成購買過程”。電子商務推薦在網絡經濟環境下不僅可以將電子商務系統的瀏覽者轉變為購買者，促進產品交叉銷售能力，還可以提高客戶的忠誠度，在市場競爭日趨激烈的今天顯得尤為重要[18-19]。電子商務推薦功能實現的好壞主要決定于其采用的推薦技術，已有推薦算法的相似性計算方法在遇到稀疏數據時有其明顯的不足，而數據缺失、數據稀疏又是電子商務銷售數據的主要特征之一。軟集中對每個參數所對應的近似集（論域U的子集）不做任何的限制，這使得軟集在處理稀疏數據時有著明顯的優勢。

本文將命題邏輯思想應用到軟集數據分析中，給出一種基于軟集和邏輯公式的信息系統屬性分析的新方法。首先，建立一種基于軟集的命題邏輯推理語言，在這種形式推理語言中，原子公式是軟集中的參數α，參數α的函數值F(α（)是論域U的子集）是原子公式α的賦值集，軟決策規則是決策軟集上的由原子公式組成的蘊含邏輯公式。其次，引進真度、條件真度、絕對真度等概念從充分性、必要性、合理性等不同方面來評價軟決策規則，將決策系統轉化為決策軟集來表示，提出不完備決策信息系統的軟決策規則提取算法。最后，將基于命題邏輯和軟集的數據分析方法應用于電子智能推薦，給出基于軟屬性關聯關系分析的智能推薦算法，并通過實際例子和數值實驗驗證本文提出的算法是有效的。

2 軟集及其誘導出的邏輯公式

論域U上的一個軟集（簡記為FS）是一個二元組S=(F,A)，其中，E是參數集合，A?E，P(U)是U的冪集，F:A→P(U)是集值映射，即對e∈A，F(e)?U。如果U上有概率分布P，則稱S=(F,A)為概率軟集。顯然，一般的軟集在等概率分布P({u})=1|U|下可以看作為概率軟集。論域U和參數集E上的全體軟集記為PE(U)。設(F,A)和(G,B)是論域U和參數集E上的兩個軟集，如果A?B，且 ?a∈A，F(a)?G(a)，則稱(F,A)是(G,B)的軟子集，記為(F,A)?(G,B)。兩個軟集(F,A)和(G,B)的并定義為(H,C)=(F,A)?(G,B)，其中C=A?B，當a=A-B時，H(c)=F(c)；當 a=B-A時 ，H(c)=G(c)；當a=A?B時，H(c)=F(c)?G(c)。同樣，兩個軟集(F,A)和(G,B)的交定義為(H,C)(=F,A)?(G,B)，其中C=A?B，對a=C，H(c)=F(c)?G(c)[2]。

信息系統（也稱為數據庫系統）是一個三元組I=(U,A,V，)其中U是對象集，A是屬性集，V是屬性值集合，V(a)是屬性a的值域，每個屬性a∈A都相應地確定一個函數a:U→V(a，)它指定了U中每個對象u的屬性值。如果信息系統的屬性集A被劃分為C和D兩部分，則稱I=(U,C?D,V)為決策信息系統，并稱C中的元素為條件屬性，D中的元素為決策屬性[17]。

以上介紹的軟集和信息系統這兩個概念之間有著密切的聯系。首先，論域U上的一個軟集S=(F,A)可以通過一種自然的方式誘導出一個信息系統IS=(U,A,{0,1}，)對每一個a∈A，如果u∈F(a)，則a(u)=1，否則a(u)=0其次，設I=(U,A,V)是信息系統，則每一個a∈A都可以誘導出一個軟集Sa=(Fa,Ba)，其中Ba={a}×V(a)，對任何(a,t)∈Ba，Fa(a,t)={u∈U:a(u)=t}；而信息系統I誘導出一個軟集 S=(F,B)，其 中對 (a,v)∈B，F(a,v)={u∈U:a(u)=v}。顯然，{Fa(a,t):(a,t)∈Ba}構成論域U的一個劃分，而{F(a,v):(a,v)∈B}構成論域U的一個覆蓋[20]。

以下給出本文要用到的基于軟集的軟邏輯公式及其賦值等概念。

首先，回顧一下命題邏輯公式及其賦值的概念。設Q={q1,q2,…}為原子公式集，F(Q)是由Q生成的(?,∧,→ 型)自由代數，稱F(Q)中的元素為邏輯公式，簡稱為公式。設B={0,1}是標準布爾代數，則B={0,1}亦是(?,∧,→ 型)代數。自由代數(F(Q);?,∧,→)和B={0,1}之間的(?,∧,→ )型同態v:F(S)→{0,1}稱為F(Q)的邏輯公式的賦值，對α∈F(Q)，v(α)稱為公式α的值[21-22]。

設S=(F,A)是論域U和參數集E上的軟集，稱α∈A為基于軟集S的軟原子公式（為了與軟集參數和信息系統屬性術語相區別，以下用小寫希臘字母作為軟原子命題的標識符）。由全部原子公式生成的(?,∧,→ )型自由代數記為F(S)，F(S)中的元素稱為基于軟集S的軟邏輯公式（為了與數理邏輯中邏輯公式概念相區別，本文稱之為軟邏輯公式），也就是說，F(S)是由A中的元素經過下列步驟所生成：（1）A?F(S)；（2）若φ∈F(S)，則?φ∈F(S)；（3）若φ,ψ∈F(S)，則φ∧ψ，φ→ψ∈F(S)；（4）λ∈F(S)當且僅當λ可經過以上3步有限次所產生[20]。

對軟集(F,A)，如果A被劃分為C和D(即A=C? D,C ?D=?)，此時也記軟集(F,A)為(F,C? D)，并稱之為決策軟集。顯然，決策軟集SC=(F,C)和SD=(F,D)都是(F,C?D)的軟子集，分別稱之為條件軟子集和決策軟子集，并稱相應的軟邏輯公式FA(SC)和F(SD)為條件屬性公式和決策屬性公式[20]。

設(F,A)是論域U上的軟集，由于F(S)是由原子公式集A生成的(?,∧,→型)自由代數，因此，對每一個u∈U，映射可惟一決定公式集F(S)上的一個賦值vu:F(S)→{0,1}，這里 χF(α)(u)表示集合F(α )的特征函數。設φ∈F(S)，如果vu(φ)=1，借用數理邏輯中的術語，稱vu為公式φ的模型（也稱u支持公式φ），記為，并稱為公式φ∈F(S)的軟集合語義解釋。顯然，對每一個原子公式α∈A，有，當且僅當如果，則稱φ為軟重言式；如果，則稱φ為軟矛盾式。設φ,ψ∈F(S)，如果對全部的賦值vu，有vu(φ)=vu(ψ)，則稱φ與ψ軟邏輯等價。

關于軟邏輯公式的軟集合語義解釋，有下面的結論。

命題1[20]設(F,A是)論域U上的軟集，φ,ψ∈F(S)，則：

從形式上看，命題1與粗糙集理論中的決策邏輯中公式解釋相似，但其實它們定義的途徑是不一樣的，軟集合(F,A)上的任何軟邏輯公式的語義解釋

本文引入的軟邏輯公式及其語義與數理邏輯中的相應概念既有相似也有不同，相似之處是所討論的公式都是由原子公式自由生成且都是用標識符表示；不同之處是數理邏輯中用于表示原子命題的標識符沒有明確的實際意義，而軟邏輯原子公式是軟集中的參數，基于一個給定軟集的軟邏輯原子公式是有其實際含義的。另外，本文構造的軟邏輯公式的軟集合語義也可認為是文獻[22-23]命題邏輯概率語義的具體化。為了在軟邏輯語義意義下找到一種提取有用軟決策規則的有效方法，在下一章先應用文獻[22-23]的部分真度概念來刻畫一個給定的軟邏輯公式的正確程度，然后引進其他一些描述軟決策規則的度量指標。

3 軟邏輯公式的軟真度

定義1設S=(F,A)是有限論域U上的概率軟集，P是U上的正規概率分布，即?u∈U，P({u})，>0，對于給定的邏輯公式φ，稱

為軟邏輯公式φ基于軟集S的基本軟真度（basic soft truth degree，BSTD）。

注意到vu(φ)=1意味著u支持φ，因此τ(?)可以被看作一種“投票模型”。由于在實際的數據處理中軟集通常是用表格表示的，這時對象u的概率P({u})其實就是與u有相同參數及參數值的對象數目與全體對象數的比值，而公式φ的軟真度其實就是支持φ的對象的概率和。一個軟邏輯公式的可靠性通過軟真度被程度化并且這種程度化是由支撐軟邏輯公式的基礎軟集所確定。

命題2（1）0≤τ(φ)≤1；

（3）若φ與ψ軟邏輯等價,則τ(φ)=τ(ψ)；

（4）τ(?φ)=1-τ(φ)；

（5）τ(φ∨ψ)=τ(φ)+τ(ψ)-τ(φ∧ψ)。

證明（1）～（3）的證明是容易的，下證（4）和（5）。

設(F,C?D)為決策軟集，稱形如φ→ψ的邏輯公式為軟決策規則，其中φ∈F(SC)，ψ∈F(SD)。當φ、ψ分別只是C、D中的原子公式時，稱φ→ψ為基本軟決策規則；如果φ、ψ分別包含C、D的全部原子公式，則稱φ→ψ為典型軟決策規則。當φ→ψ是軟重言式時，也記φ→ψ為φ?ψ。顯然，φ?ψ當且僅當。因此，當時，總有φ?ψ，這在邏輯上是有效的，但從實際推理應用的角度來看卻不是合法的。在屬性關聯關系分析中，既要關心所提取軟決策規則的邏輯有效性，同時還需關心軟決策規則實際應用中的合法性。基于這個原因，以下引進一些軟真度來刻畫軟決策規則的合法性和可行性。

定義2設(F,C?D)是有限論域U上的概率決策軟集，P是U上的正規概率分布。

（1）當τ(φ)≠0時，定義軟決策規則φ→ψ基于軟集S的條件軟真度（conditional soft truth degree,CSTD）為：

（2）定義軟決策規則φ→ψ基于軟集S的絕對軟真度（absolute soft truth degree，ASTD）為：

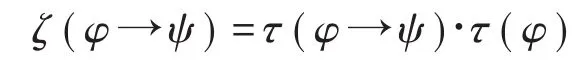
通常也稱ζ(φ→ψ)為軟決策規則φ→ψ的絕對充分軟真度（absolute sufficient soft degree，ASSD），而稱軟邏輯公式ψ→φ的ζ(ψ→φ)為軟決策規則φ→ψ的絕對必要軟真度（absolutenecessarysoftdegree，ASND）。當前件φ的軟真度τ(φ)≠0時，軟決策規則φ→ψ的條件軟真度γ(φ→ψ)可以被理解為在給定前件φ的條件下后件ψ為真的條件概率，它表示軟決策規則φ→ψ的強度，描述了規則的置信程度。軟決策規則φ→ψ的絕對軟真度ζ(φ→ψ)由兩部分組成，它們分別從兩個不同方面對軟決策規則進行刻畫。從關聯規則提取的角度看，前一部分τ(φ→ψ)關注于所收集的數據對軟決策規則的支持強度，后一部分τ(φ)關注于所收集的數據對軟決策規則前件的支持強度。從程度化邏輯語義、近似推理的角度看，τ(φ→ψ)著重考慮軟決策規則的有效程度，它描述的是軟決策規則的有效性，τ(φ)著重考慮軟決策規則的合法程度，它描述的是軟決策規則的合法性。因此，絕對軟真度ζ(φ→ψ)從整體上刻畫了軟決策規則φ→ψ的有效性和合法性，這正符合軟決策規則在實際應用中既需要考慮它的有效性，還要關注其合法性的需要。值得指出的是，利用絕對軟真度可以排除那些偽真的軟決策規則。如，對于一個軟決策規則φ→ψ，前件φ的基本軟真度τ(φ)=0，即使有τ(φ→ψ)=1，這種偽真的軟決策規則在應用中其實是沒有意義的，而絕對軟真度ζ(φ→ψ)=0則剛好可以刻畫這種應用中的實際情況。

命題3設(F,C?D)是有限論域U上概率決策軟集，φ→ψ是軟決策規則，則下列條件等價：

（1）φ→ψ是軟重言式；

（2）τ(φ→ψ)=1；

（3）ζ(φ→ψ)=τ(φ)；

（4）τ(φ)=0或γ(φ→ψ)=1。

證明(1)?(2)設φ→ψ是軟重言式，則。由命題1（4），有：

(2)? (3)是顯然的。

(3)? (4)由ζ(φ→ψ)=τ(φ)，知τ(φ→ψ)=1。從而由命題2（2），有此時當然有從而φ→ψ是軟重言式。若γ(φ→ψ)=1，則τ(φ∧ψ)=τ(φ。)由P是U上正規概率分布和有，故有，于是，從而

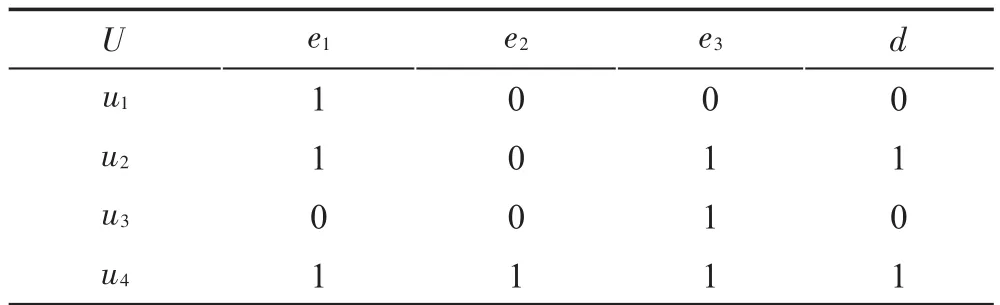
Table 1 Probabilitydecisionsoftset(F,C?D)表1 概率決策軟集(F,C?D)

從而φ→ψ是軟重言式。

例1一個概率決策軟集(F,C?D)如表1。其中，U={u1,u2,u3,u4}，U上的正規概率分布為：P({u1})= 1 3 ，P({u2})=1 3，P({u3})=1 6，P({u4})=1 6，條件參數集C={e1,e2,e3}，參數的含義為 e1=“頭痛”，e2=“肌肉痛”，e3=“發燒”，決策參數集D=g0gggggg，參數的含義為d=“流感”。

各軟決策規則BSTD為：

各軟決策規則CSTD為：

各軟決策規則ASTD為：

注1（1）一個軟決策規則的三個真度值從三個不同角度描述了軟決策規則的數值特性。一般來說，基本軟真度關注的是軟決策規則的有效性；條件軟真度強調條件屬性與決策屬性之間的蘊含關系的確定性；絕對軟真度同時考慮了軟決策規則的合法性和條件屬性對軟決策規則的支持強度。

（2）從例1也可以看到，雖然軟決策規則e2→d的有效性和確定性都很高（強度為1），軟決策規則e2→d中的條件屬性e2對軟決策規則的支持強度很低（強度為1 6）。直觀地說，可以理解為：由于u2也滿足e1和e3，從而支持軟決策規則e2→d的證據u2實際上可能不起作用。換句話說，u2的“流感”與“頭痛”或“發燒”有關，而不是他的“肌肉痛”。

（3）根據數理邏輯的MP規則，當然有φ∧(φ→ψ)?ψ。當φ→ψ和φ是軟重言式時，有τ(φ→ψ)=1和τ(φ)=1，從而ζ(φ→ψ)=。1因此，從某種意義上說，絕對軟真度是一個由軟決策規則φ→ψ和其前件φ的基本軟真度來共同刻畫后件ψ的真度概念。

定義3設S=(F,A)是有限論域U上的概率軟集，對于給定的邏輯公式 φ、ψ，稱 η(φ,ψ)=τ((φ→ψ)∧(ψ → φ))為邏輯公式φ、ψ的軟相似度。當η(φ,ψ)=1時，稱軟邏輯公式φ與ψ是軟相似的。

命題4設φ,ψ∈F(S)，則：

（1）η (φ,ψ )=η (ψ,φ )；

（2）若φ與ψ邏輯等價，則φ與ψ是軟相似的。

命題4的證明是顯然的。

命題5設S=(F,A)是有限論域U上的概率軟集,φ,ψ,ζ∈ F(S)，記 ρ(φ,ψ )=1-η (φ,ψ )，則：

（1）ρ(φ,φ )=0

（2）ρ(φ,ζ)≤ρ(φ,ψ)+ρ(ψ,ζ)

因此，ρ是F(S)上的偽距離，稱之為軟邏輯距離，并稱(F(S),ρ)為軟邏輯距離空間。

證明（1）是顯然的。下面證明（2）。因τ(φ)=可表示為所以：

又由于：

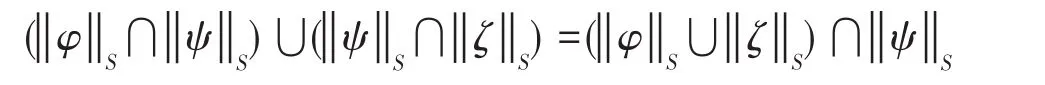
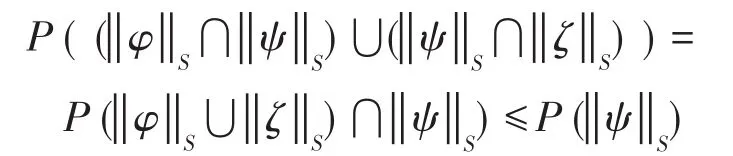
故得：因此，有：

于是：

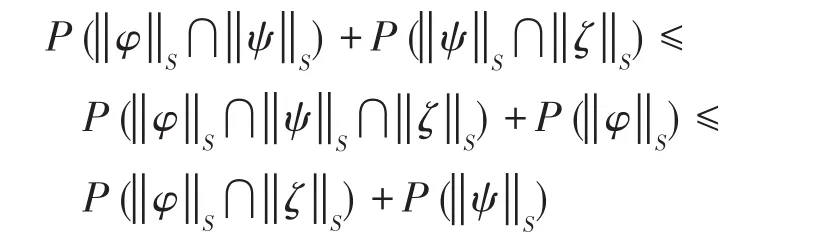
因此：

4 基于軟邏輯的決策分析方法

對于一個給定的信息系統，分析屬性之間的關聯關系，尤其是在決策信息系統中，分析條件屬性值和決策屬性值之間的因果關系是系統分析的一個重要方面。從形式邏輯上看，一個軟決策規則就是一個含有蘊含聯結詞的軟邏輯公式，本章給出一個基于軟邏輯的決策分析方法。

算法1基于軟邏輯的典型軟決策規則軟真度分析算法（soft truth analysis algorithm，STAA）

輸入：決策信息系統(U,C? D,V),U上的正規概率分布P。

輸出：典型軟決策規則及其真度。

步驟1輸入條件屬性C={a1,a2,…,al},決策屬性D=g0gggggg。

步驟2構造軟集Sai(i=1,2,…,l)和Sb。

步驟3計算軟集Sai(i=1,2,…,l)和Sb的并決策信息系統(U,C ? D,V)被轉化為U上的決策軟集S=(F,CS?DS)，條件參數集為CS={(ai,ri):i=1,2,…,l,ri∈Vai},決策參數集為 DS={(d,t):t∈ Vb}。

步驟4對每個ri∈Vai(i=1,2,…,l)和t∈ Vb，計算軟決策規則(a1,r1)∧(a2,r2)∧…∧(al,rl)→(d,t)的BSTDτ((a1,r1)∧(a2,r2)∧…∧(al,rl)→(d,t))。

步驟 5對每個ri∈Vai(i=1,2,…,l)和t∈Vb，計算軟決策規則 (a1,r1)∧(a2,r2)∧…∧(al,rl)→(d,t)的CSTDγ((a1,r1)∧(a2,r2)∧…∧(al,rl)→(d,t))。

步驟 6對每個ri∈Vai(i=1,2,…,l)和t∈Vb，計算軟決策規則(a1,r1)∧(a2,r2)∧…∧(al,rl)→(d,t)的 ASTD ζ((a1,r1)∧(a2,r2)∧…∧(al,rl)→(d,t))。

步驟 7計算 (b,t)→(a1,r1)∧(a2,r2)∧…∧(al,rl)的ASTD得到軟決策規則(a1,r1)∧(a2,r2)∧…∧(al,rl)→(d,t)的ASND。

例2關于病人決策信息系統的軟決策規則分析，一個病人決策信息系統如表2。

Table 2 Patientdecision-makinginformationsystem表2 某些病人決策信息系統

為了方便描述，分別將上述屬性及屬性值符號化，其中a=“頭痛”，b=“肌肉痛”，c=“體溫”，d=“流感”。

Table 3 Reduced and symbolized decision soft set表3 約簡和符號化后的決策軟集

a=“頭痛”的兩個屬性值是、否分別用a1、a2表示；b=“肌肉痛”的兩個屬性值是、否分別用b1、b2表示；c=“體溫”的三個屬性值很高、高、正常分別用c1、c2、c3表示；d=“流感”的兩個屬性值是、否分別用d1、d2表示。利用粗糙集理論對信息系統進行屬性約簡，得到最小屬性約簡集為{頭痛(a),體溫(c)}。將約簡和符號化后的屬性表轉化為軟決策集如表3。

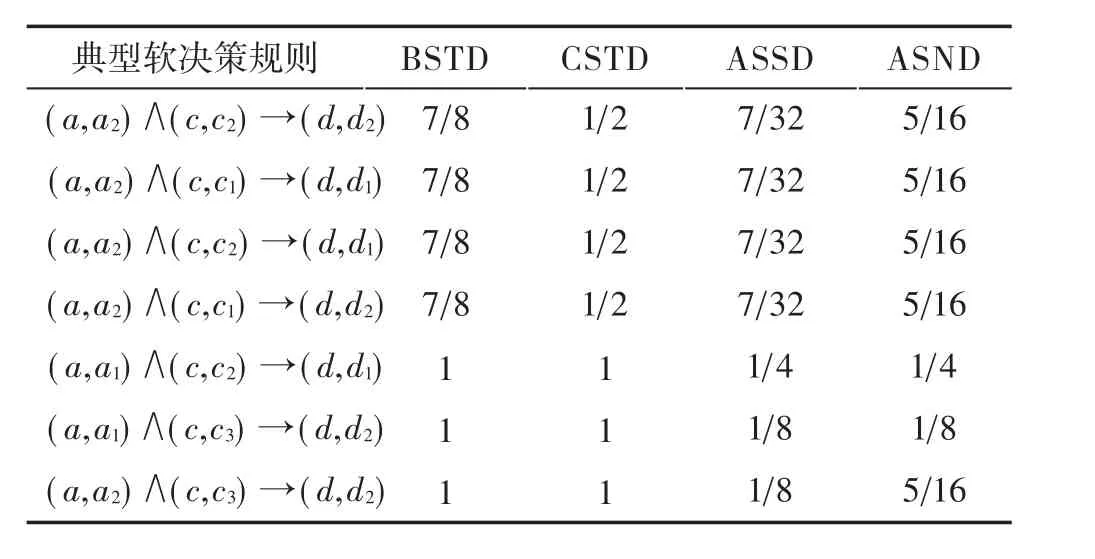
Table 4 Soft truth of typical soft decision rules表4 典型軟決策規則的軟真度分析

由條件和決策原子公式可以組成12條典型軟決策規則，在不設定閾值情況下，BSTD大于0的典型軟決策規則共有7條，這些典型軟決策規則的軟真度分析如表4。

從表4的計算結果，可以得到關于流感病人的更多信息。比如，可以說“頭痛且體溫高比頭不痛且體溫很高的人更可能患有流感”，因為軟決策規則的CSTD表明：

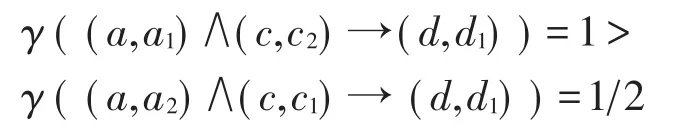
Fig.1 Truth comparison between soft decision rule 1 and 2圖1 軟決策規則1和2的真度比較

從數據分析的角度看，上述結果意味著大約有100%的頭痛且體溫高的人患有流感，而只有50%的頭不痛且體溫很高的人患有流感。此外，結論“頭痛且體溫高比頭不痛且體溫很高的人更可能患有流感”可以通過ASSD得到進一步的證實，因為：

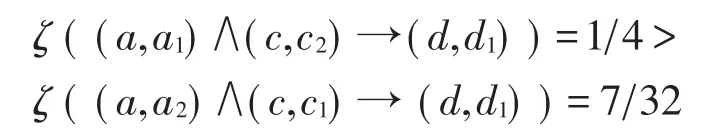
以上的分析結果可通過圖1進一步說明，在圖中，軟決策規則1和2分別表示(a,a1)∧(c,c2)→(d,d1)，(a,a2)∧(c,c1) →(d,d1)。

5 基于軟決策分析的智能推薦方法及實例分析

本章在以上分析基礎上，提出一個基于軟決策分析的智能推薦方法并給出實例分析。為了表述的方便，以下通過電子商務推薦對該方法進行敘述，該推薦方法完全可以類似地應用于智慧旅游等其他智能推薦場合。該推薦方法是在已有用戶購買電商產品信息的基礎上，給那些有潛在購買意向的用戶推薦電商產品，推薦的依據是用戶有興趣的電商產品信息，推薦的基本思想是認為對一些電商產品具有相同興趣的用戶對另一電商產品也具有相同的興趣。推薦過程如下：（1）將用戶已購買或已評價的電商產品作為條件屬性，待推薦電商產品作為決策屬性，構造決策信息系統。（2）將決策信息系統轉化為決策軟集。（3）將同時包含有條件屬性和決策屬性的對象（用戶）作為典型軟決策規則挖掘的基礎集（稱之為訓練集），依據訓練集挖掘出全部典型軟決策規則。（4）將只包含有條件屬性而不包含決策屬性的對象（用戶）作為推薦的基礎集（稱之為推薦集），挖掘出與推薦集相對應的條件屬性公式。（5）按照條件屬性公式與已挖掘出的典型軟決策規則的條件屬性公式之間的軟邏輯偽距離的大小，激活典型軟決策規則，利用所激活的典型軟決策規則，采用邏輯推理的方式給出電商產品的推薦。

算法2基于軟決策分析的推薦算法（soft decision analysis recommendation algorithm，SDARA）

輸入：信息系統(U,A)，對象集U是電商客戶，屬性集A是用戶已評價（或購買）的電商產品，閾值α、β。

輸出：滿足閾值要求的推薦結果。

步驟1構造決策信息系統(U,C?D)，條件屬性C是用戶已購買電商產品，決策屬性D是待推薦電商產品。

步驟2將決策信息系統(U,C?D)轉化為決策軟集(F,C?D)。

步驟3依據所得到決策軟集(F,C?D)，應用算法STAA，挖掘得到全部如下形式的典型軟決策規則其 中 ri∈Vai(i=1,2,…,l)是作為條件屬性值的電商產品，t∈Vb是待推薦的作為決策屬性值的電商產品。

步驟4應用算法STAA，提取BSTD和ASTD分別滿足閾值α、β的典型軟決策規則（比如(a1,r1)∧(a2,r2)∧…∧(al,rl)→(d,t)，由于應用的是軟邏輯公式概念，提取的典型軟決策規則所包含的條件屬性原子公式個數l可以不一致）。

步驟5對于一個給定的只包含有條件屬性的待推薦公式 (c1,s1)∧(c2,s2)∧…∧(ck,sk)，其中 si∈Vci(i=1,2,…,k)，計算(c1,s1)∧(c2,s2)∧…∧(ck,sk)與步驟4所提取的典型軟決策規則前件（如(a1,r1)∧(a2,r2)∧…∧(al,rl)）之間的軟邏輯距離（由于應用的是軟邏輯公式概念，這些前件包含的原子公式個數，待推薦公式包含的原子公式個數都可以不相同）。

步驟6選擇上一步計算出的最小軟邏輯距離，設有最小軟邏輯距離的典型軟決策規則的前件為，選擇典型軟決策規則。

步驟7如果有多條典型軟決策規則的前件為，則計算 這 些典型 軟決策規則的CSTD，激活有最大CSTD的軟決策規則

步驟8將步驟7激活的典型軟決策規則的 前 件 代 換為待推薦公式，得到推薦規則(c1,s1)∧(c2,s2)∧…∧(ck,sk)→(d(0),t(0))。

步驟9按照推薦規則(c1,s1)∧(c2,s2)∧…∧(ck,sk)→ (d(0),t(0))得出推薦結果 (d(0),t(0))。

注2算法SDARA是基于待推薦軟邏輯公式與已有公式的最小軟邏輯距離來產生推薦規則，而軟邏輯距離是通過真度來進行計算的。因此，從推薦方法分類的角度，本文的推薦方法是協同過濾推薦和基于規則推薦的結合，但由于算法2是基于軟邏輯語義理論的，從而它有較強的邏輯基礎和邏輯意義，這種方法將在模式識別、近似推理等人工智能方面有著較大的應用前景。

例3考慮一個電子商務網站，用戶通過網站對電商產品評價（或購買）作出“有興趣”“沒興趣”的評價。表5是該網站的部分事務數據庫（在表中，沒興趣、有興趣分別用0、1表示，*表示沒有該用戶對該電商產品的評價數據）。用戶u3和u8對電商產品f的評價未知，網站平臺通過尋找用戶u3和u8的最近鄰關于f的評價來決定是否應該將電商產品f推薦給用戶u3和u8。

Table 5 Partial transaction data for e-commerce表5 某電子商務部分事務數據庫

Table 6 Typical soft decision rules and their soft truth表6 典型軟決策規則及其軟真度

Table 7 Softlogicaldistancebetweena1∧b0∧c1∧d1∧e0 and antecedents of typical soft decision rule表7 a1∧b0∧c1∧d1∧e0與典型軟決策規則前件的軟邏輯距離

將以上事務數據庫（信息系統）轉化為決策軟集(F,C?D)，其中C={a,b,c,d,e}，D={f}，由于本例每個屬性都只有兩個值，決策軟集(F,C?D)也可以表示為表5的形式，推薦集為{u3,u8}，訓練集為{u1,u2,u4,u5,u6,u7,u9,u10}。根據訓練集，取閾值 α=0.5,β = 0.1，應用算法SLDTA，挖掘得到的6條典型軟決策規則及其軟真度如表6。

與用戶u3相對應的軟邏輯公式為a1∧b0∧c1∧d1∧e0，它與各條典型軟決策規則前件的軟距離如表7。最小距離為0，激活相應的軟決策規則a1∧b0∧c1∧d1∧e0→f1，推薦規則為a1∧b0∧c1∧d1∧e0→f1，推薦結論：將電商產品f推薦給用戶u3。

Table 8 Soft logical distance betweenb1∧c0∧d1∧e1and antecedents of typical soft decision rule表8 b1∧c0∧d1∧e1與典型軟決策規則前件的軟邏輯距離

與用戶u8相對應的軟邏輯公式為b1∧c0∧d1∧e1，它與各條典型軟決策規則前件的軟距離如表8。最小距離為1 10，激活相應的典型軟決策規則，推薦規則為a0∧b1∧c0∧d1∧e0→f0或a0∧b1∧c0∧d1→f0,推薦結論：不將電商產品f推薦給用戶u8。

6 實驗驗證

本章通過實驗對本文提出的算法和文獻[24]的關聯規則推薦算法（下文稱之為傳統方法）的推薦準確率進行比較，進而驗證本文算法的有效性。實驗環境為Win 7 x64，Intel?3.4 GHz,RAM 4 GB。實驗數據集為Movielens公開的電影點播及評分數據集，實驗時從數據集中隨機選取5組數據，每組數據個數為1 600，按照75%∶25%的比例隨機生成訓練集和測試集，取BSTD的閾值為α=0.6，ASTD的閾值為β=0.1。由于本文只處理二值屬性，沒有涉及多屬性值，而Movielens數據集的電影評價為1～5級評分，為此，對電影評分只取“滿意”和“不滿意”兩個值，客戶評分大于或等于3分表示客戶對電影“滿意”，評分小于或等于2分表示客戶對電影“不滿意”。實驗結果的比較指標選取為推薦準確率（recommended accuracy，RA），計算公式為：

Fig.2 Comparison results of recommended accuracy RA圖2 推薦準確率RA的比較結果

實驗比較結果如圖2所示。

圖2的實驗結果顯示，從推薦的準確率方面來看，本文的推薦方法比傳統推薦方法要高一點。但正如注1所指出的，相對于傳統的推薦方法，本文方法的更大意義在于其有較強的邏輯基礎和邏輯意義。

7 結束語

軟集在不確定決策方面的研究，是目前軟集在應用研究中最活躍的方向之一。本文提出基于軟集和邏輯公式的決策信息系統軟決策規則分析方法.建立一種基于軟集的形式推理語言，在這種形式推理語言中，原子公式是軟集中的參數α，參數α的函數值是論域U的子集）是原子公式α的賦值集。通過將決策系統轉化用決策軟集來表示，軟決策規則表示為決策軟集上的由原子公式組成的蘊含邏輯公式。引進基本軟真度、條件軟真度、絕對軟真度等概念從充分性、必要性、合理性等不同方面來對軟決策規則作出評價，提出基于軟邏輯的不完備決策信息系統的決策規則提取算法。將基于軟邏輯的軟決策規則分析方法應用于電子商務智能推薦，給出基于軟屬性關聯關系分析的電商產品推薦算法，實際例子和實驗表明本文提出的算法是有效的。

本文提出的基于軟邏輯的電子商務智能推薦方法是基于用戶對電商產品作出明確的評價（購買或不購買，喜歡或不喜歡等），而無須用戶給出對電商產品打分或作其他的不確定性評價，得到的推薦結論也只有確定的推薦或不推薦。因此，可以說本文提出的智能推薦方法是一種確定的、剛性的推薦方法，這既是本文方法的優點，也可能是本文研究結論值得進一步完善之處。限于篇幅，本文所提出算法的實際應用，以及將本文方法進行推廣，即如何將用戶對電商產品評價程度考慮進來并考慮推薦的等級，討論基于模糊軟集的形式邏輯與相應的軟決策規則分析方法及其在電子智能推薦中的應用，將在另外的文章中給出。