加權(quán)好友推薦模型鏈路預(yù)測算法*

錢付蘭，楊 強，馬 闖，張燕平

1.安徽大學 計算機科學與技術(shù)學院，合肥 230601

2.安徽大學 數(shù)學科學學院，合肥 230601

3.安徽大學 信息保障技術(shù)研究中心，合肥 230601

1 引言

網(wǎng)絡(luò)已經(jīng)成為描述形形色色復雜系統(tǒng)最重要的工具之一[1]，網(wǎng)絡(luò)科學隨著社交媒體和大數(shù)據(jù)的發(fā)展，以復雜網(wǎng)絡(luò)和社交網(wǎng)絡(luò)為目標的網(wǎng)絡(luò)研究日新月異。網(wǎng)絡(luò)中的鏈路預(yù)測問題主要是根據(jù)網(wǎng)絡(luò)本身的拓撲結(jié)構(gòu)和網(wǎng)絡(luò)的外部信息尋找一些算法進行預(yù)測，估計網(wǎng)絡(luò)中未產(chǎn)生連邊的兩點之間連接邊的可能性[2]。鏈路預(yù)測作為網(wǎng)絡(luò)科學中的重要研究內(nèi)容，在眾多現(xiàn)實問題中有著廣泛的應(yīng)用背景，業(yè)已成為橫跨多個學科的核心科學問題。

無論是計算機領(lǐng)域的數(shù)據(jù)挖掘[3-4]還是社交網(wǎng)絡(luò)中的朋友推薦[5-6]，無論是恐怖分子網(wǎng)絡(luò)中的威脅發(fā)現(xiàn)還是生物領(lǐng)域中的蛋白質(zhì)交互[7]，在實際的鏈路預(yù)測應(yīng)用中，如何從現(xiàn)有的鏈路預(yù)測算法中選擇較為合適的算法或針對具體網(wǎng)絡(luò)結(jié)構(gòu)和應(yīng)用背景設(shè)計合理的算法，以取得較好的預(yù)測效果，是鏈路預(yù)測所要解決的首要問題。

常見的算法主要基于節(jié)點屬性和網(wǎng)絡(luò)局部結(jié)構(gòu)進行鏈路預(yù)測。雖然利用節(jié)點屬性等外部信息通常可以得到很好的預(yù)測效果，但是節(jié)點屬性很多時候是難以獲得的，即使獲取也經(jīng)常伴有噪聲。相比而言，網(wǎng)絡(luò)局部結(jié)構(gòu)更易獲得也更可靠[8]。因此近年來，基于網(wǎng)絡(luò)局部結(jié)構(gòu)的鏈路預(yù)測算法日益受到關(guān)注。

本文組織結(jié)構(gòu)如下：第2章介紹了一些與本文有關(guān)的鏈路預(yù)測的研究工作。第3章主要介紹本文提出的鏈路預(yù)測算法。第4章是實驗以及結(jié)果分析。第5章為結(jié)束語，總結(jié)本文的工作，對下一步研究進行展望。

2 相關(guān)工作

基于網(wǎng)絡(luò)局部結(jié)構(gòu)進行鏈路預(yù)測的算法有很多。其中，最簡單的相似性算法是共同鄰居算法[9]（common neighbor，CN），將兩個節(jié)點間的相似性定義為共同鄰居節(jié)點數(shù)。Adamic等人[10]考慮了節(jié)點間共同鄰居的度，根據(jù)共同鄰居節(jié)點的度為每個節(jié)點賦予一個權(quán)重值，提出Adamic-Adar，即AA算法。Zhou等人[11]受網(wǎng)絡(luò)資源分配過程的啟發(fā)，提出了資源分配指標（resource allocation，RA）算法，與AA算法有異曲同工之處。尹永超等人[12]考慮到不同鄰居節(jié)點對兩個終節(jié)點的影響，提出了CRA（common resource allocation）算法。基于網(wǎng)絡(luò)局部結(jié)構(gòu)的鏈路預(yù)測算法大體上可以分為如下幾方面：

（1）融合局部結(jié)構(gòu)性指標如聚類系數(shù)等提出新算法。

文獻[13]受局部結(jié)構(gòu)思想的影響，使用網(wǎng)絡(luò)共同鄰居節(jié)點的聚類系數(shù)直接表達網(wǎng)絡(luò)的局部結(jié)構(gòu)信息，提出的CCLP（clustering coefficient for link prediction）指標在預(yù)測缺失邊的效果優(yōu)于CAR（Cannistrai-Alanis-Ravai）指標。文獻[14]利用三元閉包機制結(jié)合網(wǎng)絡(luò)拓撲結(jié)構(gòu)特性，提出了一種基于三元閉包的節(jié)點相似性鏈路預(yù)測算法并且提高了預(yù)測精度。文獻[15]認為小度的鄰居節(jié)點應(yīng)該賦予較大的權(quán)值，在相似性度量中考慮所有節(jié)點和路徑，提出了PNC（path and node combined approach）算法，并且提升了基于相似性的鏈路預(yù)測算法的性能，該算法好于節(jié)點依賴性和路徑依賴性的方法。文獻[16]考慮局部信息和偏好連接的影響，提出了CN+PA（common neighbor+preferential attachment）相似性指標，并且提升了鏈路預(yù)測算法的性能。

（2）刻畫某種特殊局部特征并針對該特征提出新算法。

文獻[17]首先刻畫了網(wǎng)絡(luò)中大多存在PWCS（nodes are preferentially linked to the nodes with weak clique structure）現(xiàn)象，即節(jié)點更偏向連接具有局部群落結(jié)構(gòu)的節(jié)點。然后，該論文據(jù)此提出了一種朋友推薦模型——FR（friend recommendation）鏈路預(yù)測相似性計算指標，F(xiàn)R無論是AUC還是Precision都普遍優(yōu)于傳統(tǒng)指標。文獻[18]從信息論的角度進行鏈路預(yù)測應(yīng)用，鏈路預(yù)測中不同結(jié)構(gòu)特征的貢獻以信息的值的形式度量，并且提出了應(yīng)用多種結(jié)構(gòu)特征的信息論模型。基于此模型，該論文提出了NSI（neighbor set information）指標，優(yōu)于一些經(jīng)典的鏈路預(yù)測算法。文獻[19]通過結(jié)構(gòu)一致性指標刻畫了一個網(wǎng)絡(luò)的可預(yù)測性，并基于結(jié)構(gòu)一致性提出了一種新的鏈路預(yù)測方法，取得了很好的效果。

（3）引入社會學/傳播學等其他學科知識提出新算法。

文獻[20]引入了3步之內(nèi)為強關(guān)系，強關(guān)系引發(fā)行為的社會學知識，在考慮2步路徑上的節(jié)點（共同鄰居節(jié)點）對鏈接產(chǎn)生貢獻的同時又考慮了3步路徑上的節(jié)點的貢獻，提出了CCN（cohesive common neighbors）相似性指標并且取得了較好的預(yù)測效果。文獻[21]提出了一種假設(shè)，即每個節(jié)點吸引鏈路的能力不僅依靠其結(jié)構(gòu)重要性，而且依靠其當前的流行度（活躍度）。然后，該論文提出了一種稱為PBSPM（popularity based structural perturbation method）的新方法。在6個演化網(wǎng)絡(luò)上的實驗表明提出的方法在精度和魯棒性上優(yōu)于最新的方法。文獻[22]定義了一種稱為社團相關(guān)性指標的社團相似性特征，這一特征使用了不同社團間的直接信息和潛在信息。然后該論文為了預(yù)測缺失邊，提出了一種基于社團相關(guān)性的新算法。實驗表明提出的方法具有更有效的預(yù)測精度，社團相關(guān)性特征使得預(yù)測的時間復雜度更低。

在上面幾種基于網(wǎng)絡(luò)局部結(jié)構(gòu)進行鏈路預(yù)測的算法中較為常見的是將網(wǎng)絡(luò)局部特性和依據(jù)社會學/傳播學中網(wǎng)絡(luò)節(jié)點信息相結(jié)合，獲得較為合理有效的鏈路預(yù)測策略，或針對某一網(wǎng)絡(luò)結(jié)構(gòu)特征構(gòu)建適合該特征的鏈路預(yù)測算法。上述所提的FR算法基于好友推薦策略，中間人無差別將自身的好友介紹給目標用戶，該過程與真實社交行為并不相符。因此本文利用真實社交網(wǎng)絡(luò)好友推薦策略，中間人傾向于將自己更熟悉的人介紹給目標用戶，提出了一種節(jié)點相似性度量指標。該指標結(jié)合局部特征描述并有效區(qū)分了用戶節(jié)點之間影響力的不同，更適用于PWCS這類特定的局部群落結(jié)構(gòu)。依據(jù)該指標提出的加權(quán)朋友推薦模型鏈路預(yù)測算法（link prediction algorithm based on weighted friend recommendation model，WFR）在12個公用數(shù)據(jù)上的實驗結(jié)果表明其預(yù)測效果在AUC和Precision兩個指標上都有較大的優(yōu)勢，在符合PWCS現(xiàn)象的網(wǎng)絡(luò)中優(yōu)勢更為顯著。本文最后通過對一般的人工數(shù)據(jù)上的實驗，進一步討論了WFR算法的適用范圍。

3 算法描述

本文利用兩個節(jié)點間共同鄰居的數(shù)目來描述其連邊的強弱。如果兩個節(jié)點間的共同鄰居數(shù)大于閾值α,則將這兩個節(jié)點的連邊稱為強連接，否則就為弱連接。以圖1中的無向圖為例，這里選取α=3,圖1①～③中節(jié)點A、B、C組成的連通子圖可以轉(zhuǎn)化為圖1④～⑥簡單情況。其中，粗線表示強連接邊，細線表示弱連接邊。

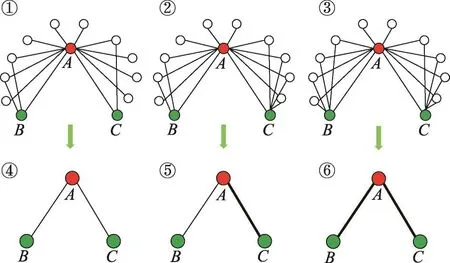
Fig.1 Transformation diagrams of 3 connected subgraphs圖1 3種連通子圖轉(zhuǎn)換圖

圖2為包含3個節(jié)點的所有區(qū)分強弱連接的7個連通子圖Ni,i=1,2,…,7（粗線表示強連接，細線表示弱連接）。P1、P2、P3分別是圖2子圖中有兩條強連接邊；圖2子圖中有一條為強連接邊，另一條為弱連接邊；圖2子圖中有兩條弱連接邊時，其余邊相連接的概率。如式（1）～式（3）所示：

Fig.2 7 possible connected subgraphs with 3 nodes圖2 包含3個節(jié)點的7個可能的連通子圖

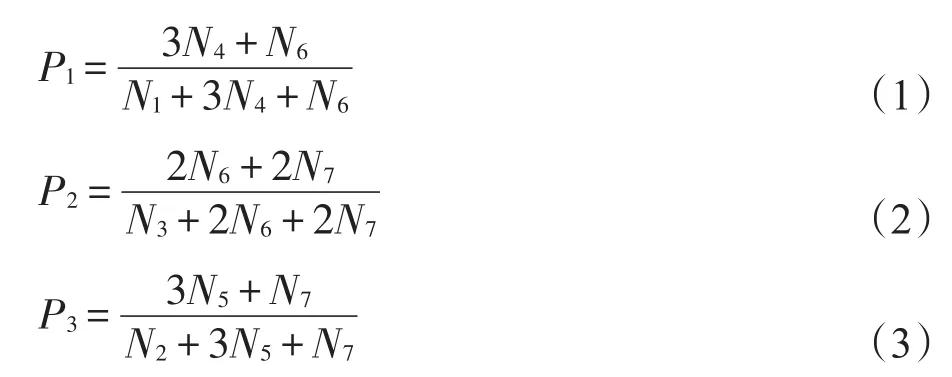
其中，P1中N4的系數(shù)為3，表示在兩條強連接邊的情形下，子圖N4上取一條邊為測試邊的方式有3種。P2分子中N6的系數(shù)為2表示有且只有其中的一條為強連接邊的情形下，子圖N6上取一條邊為測試邊的方式有兩種。以此類推得到式（1）～式（3）。

若P1＞P2且P1＞P3，說明網(wǎng)絡(luò)節(jié)點間趨向于更緊密的局部連接，可以認為PWCS現(xiàn)象存在于網(wǎng)絡(luò)中。若P1＞P2＞P3，可以認為PWCS現(xiàn)象是最明顯的。當P1＞P3≥P2時，PWCS現(xiàn)象不明顯。

基于PWCS現(xiàn)象提出的FR[17]算法通過式（4）計算節(jié)點l將自己的鄰居節(jié)點i介紹給另一個鄰居節(jié)點j的可能性。

式中，l為中介節(jié)點，j為目標節(jié)點，i為候選節(jié)點，且j和i均是l的鄰居節(jié)點。其中，k(l)為中介節(jié)點l的度，Γ(l)為節(jié)點l的鄰居節(jié)點集合，|Γ(l)?Γ(j)|表示中介節(jié)點l與目標節(jié)點j的共同鄰居節(jié)點數(shù)。分母中的“-1”是因為中介節(jié)點l不會推薦目標節(jié)點j給j,而“-|Γ(l)?Γ(j)|”表示當中介節(jié)點l推薦其相連的候選節(jié)點給目標節(jié)點j時，應(yīng)該排除l和j的共同朋友。

由式（4）可得，分母為通過中介節(jié)點l推薦給目標節(jié)點j的所有候選節(jié)點i的個數(shù)，即中介節(jié)點l介紹給目標節(jié)點j的所有候選節(jié)點i的概率均相等，而實際情況中不同的候選節(jié)點i和中介節(jié)點l的親疏程度存在著明顯的差異。如圖3所示，按照FR算法，候選節(jié)點1和節(jié)點4通過中介節(jié)點2推薦給目標節(jié)點6的概率是相同的，然而真實情況中節(jié)點4更容易被節(jié)點2推薦給節(jié)點6，即與中介節(jié)點l越相似的節(jié)點i，越容易被推薦給目標節(jié)點j。基于上述觀點，本文提出一種基于加權(quán)好友推薦模型的鏈路預(yù)測算法，利用權(quán)重對候選節(jié)點和中介節(jié)點間的親疏關(guān)系加以描述區(qū)分，稱為 WFR（weighted friend recommendation）算法。設(shè)表示這種親疏關(guān)系：

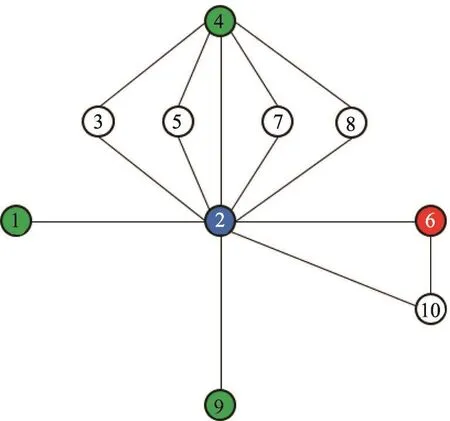
Fig.3 Asimple network圖3 一個簡單網(wǎng)絡(luò)

節(jié)點i和節(jié)點j的相似性可以定義為：

WFR算法

輸入：無向無權(quán)網(wǎng)絡(luò)network。

輸出：評價指標結(jié)果（AUC、Precision）。

開始

1.輸入訓練數(shù)據(jù)集。

2.統(tǒng)計被預(yù)測節(jié)點對(i,j)的共同鄰居節(jié)點common_nodes。

3.根據(jù)式（6）計算被預(yù)測節(jié)點對(i,j)之間的相似度SWFRij。最后求得相似度矩陣SIM。

4.根據(jù)相似度矩陣SIM和測試數(shù)據(jù)集計算評價指標的結(jié)果。

結(jié)束

4 實驗與結(jié)果

本文使用AUC（area under the receiver operating characteristic curve）[23]和精確度[24]（Precision）來評價算法性能，其中Precision排序列表長度為100。實驗隨機將原網(wǎng)絡(luò)劃分為訓練集train和測試集test，其中訓練集占90%，測試集占10%。

4.1 實驗數(shù)據(jù)和對比算法

4.1.1 實驗數(shù)據(jù)

本文使用Matlab軟件作為實驗平臺，采用線蟲的神經(jīng)網(wǎng)絡(luò)（C.elegans）[25]、爵士音樂家合作網(wǎng)絡(luò)（Jazz）[26]、美國航空網(wǎng)絡(luò)（USAir，http：//vlado.fmf.uni-lj.si/pub/networks/data/mix/USAir97.net）、蛋白質(zhì)相互作用網(wǎng)絡(luò)（Yeast）[27]、政治博客網(wǎng)絡(luò)（PB）[28]、Facebook社交網(wǎng)絡(luò)（FB，http：//snap.stanford.edu/data/）、電力網(wǎng)絡(luò)（Power）[25]、路由器網(wǎng)絡(luò)（Router）[29]以及4個食物鏈網(wǎng)絡(luò)（FWFD、FWEW、FWMW、FWFW）（http：//vlado.fmf.uni-lj.si/pub/networks/data/bio/foodweb/foodweb.htm）。如表1所示，12個網(wǎng)絡(luò)中，F(xiàn)WFD、FWEW、FWMW、FWFW、C.elegans、PB、Power和Router這8個網(wǎng)絡(luò)中P1＞P2＞P3（用斜體表示），這些網(wǎng)絡(luò)中PWCS現(xiàn)象更加明顯。

4.1.2 對比算法

4.2 實驗結(jié)果分析

為了有效驗證WFR算法的性能和適用范圍，實驗由如下三部分組成。

（1）相似性指標的選取對算法的影響。

這部分實驗通過在式（5）中代入多種相似性指標，驗證WFR算法中加入權(quán)重指標的性能。

（2）權(quán)重比例變化對算法的影響。

考察權(quán)重對算法的影響，通過調(diào)節(jié)權(quán)重比例，觀測WFR算法在AUC和Precision上的性能。

（3）人工生成的典型網(wǎng)絡(luò)環(huán)境下算法的適用分析。

考察在人工生成的典型網(wǎng)絡(luò)：一般的小世界網(wǎng)絡(luò)和規(guī)則網(wǎng)絡(luò)中，WFR算法的適用情況。

4.2.1 相似性指標的選取對算法的影響

式（5）中分別使用CN、AA、RA來計算中介節(jié)點和候選節(jié)點間的親疏關(guān)系性權(quán)重Sil,分別為：

與之相對應(yīng)的WFR算法分別記為WFR-CN、WFR-AA、WFR-RA，與一般的鏈路預(yù)測經(jīng)典算法的比較結(jié)果如表2所示。從表2得到，WFR相對于FR和經(jīng)典算法而言整體性能較好。尤其是在具有顯著PWCS特性的8個網(wǎng)絡(luò)（相關(guān)數(shù)據(jù)用斜線表示）：FWFD、FWEW、FWMW、FWFW、C.elegans、PB、Power和Router中，無論權(quán)重Sil如何計算，WFR算法均具有明顯優(yōu)勢。其中WFR-CN這一相似性指標使用計算共同鄰居的CN，更符合PWCS結(jié)構(gòu)的定義，效果最優(yōu)。表2中加粗字體表明效果最好。

圖4（a）是對圖3依據(jù)圖1進一步抽象化后得到的簡單連通子圖。目標節(jié)點與中介節(jié)點連接可強可弱，因而圖4（b）給出了另一種情形及其抽象化后的連通子圖。根據(jù)式（1）～（3），圖4（a）中邊（2,4）為強連接，邊（2,6）為弱連接，邊（2,1）為弱連接，邊（4,6）連接的概率為P2,邊（1,6）連接的概率為P3;若要得到候選節(jié)點4與6連接的概率大于候選節(jié)點1與6連接的概率需要滿足條件P2＞P3;同理，圖4（b）中需要滿足條件P1＞P2。顯然WFR通過加權(quán)進一步強化了關(guān)系P1＞P2＞P3,在具有PWCS現(xiàn)象顯著存在的網(wǎng)絡(luò)中WFR可以得到較好的結(jié)果。

4.2.2 權(quán)重比例變化對算法的影響

為了進一步考察權(quán)重對預(yù)測效果的影響，式（6）進一步被改寫為式（16）的形式，記為GWFR（generalized weighted friend recommendation）指標。

Table 2 Results ofAUC and Precision on 12 real-networks表2 12個真實網(wǎng)絡(luò)上AUC、Precision的結(jié)果

圖5給出了12種不同網(wǎng)絡(luò)中隨著α取值的不同，式（16）中GWFR相似性指標(Sil,Sjl)分別取CN、AA、RA時（分別表示為GWFR-CN、GWFR-AA、GWFRRA），與GFR指標在Precision上的比較結(jié)果。圖5給出了P1、P2、P3取值的柱狀圖，由圖5可以得到在符合P1＞P2＞P3的顯著PWCS現(xiàn)象的網(wǎng)絡(luò)中，不論α的取值如何，3種加權(quán)的GWFR算法效果都明顯好于GFR算法。當α=1時，GWFR即為WFR，GFR即為FR。

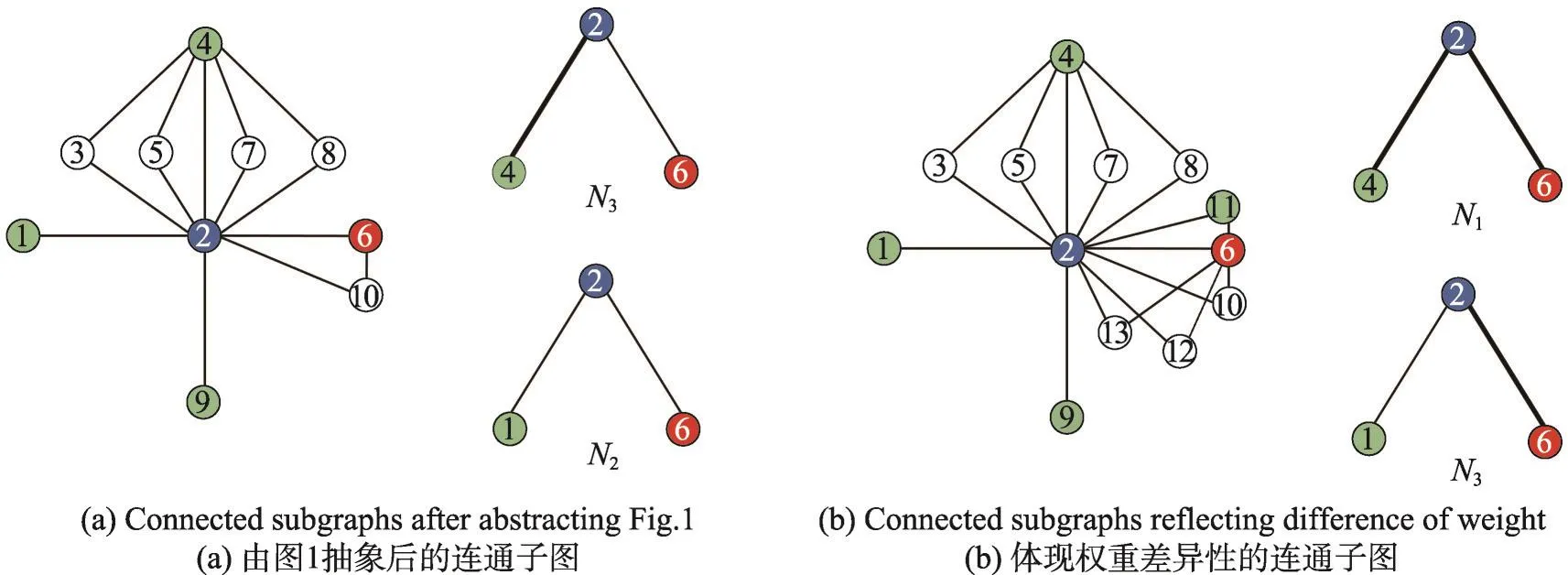
Fig.4 Analysis of effect of WFR algorithm on PWCS phenomenon圖4 WFR算法對PWCS現(xiàn)象的影響分析

4.2.3 人工生成的典型網(wǎng)絡(luò)環(huán)境下算法的效果

真實網(wǎng)絡(luò)中的一些特征很難發(fā)現(xiàn)，提供一個適合所有網(wǎng)絡(luò)的鏈路預(yù)測算法是非常困難的。本文考慮了兩種典型網(wǎng)絡(luò)生成模型——小世界網(wǎng)絡(luò)和規(guī)則網(wǎng)絡(luò)，對WFR算法的普適性進行考察。本文使用NW（Newman-Watts）小世界構(gòu)造算法設(shè)置不同的參數(shù)生成了10個小世界網(wǎng)絡(luò)，參數(shù)K的功能是調(diào)節(jié)網(wǎng)絡(luò)的平均度，參數(shù)p的功能是調(diào)節(jié)網(wǎng)絡(luò)的平均聚類系數(shù)，其特征信息如表3所示，本文設(shè)置網(wǎng)絡(luò)的節(jié)點數(shù)N=1 000,其中每個節(jié)點都與它左右相鄰的各K/2個節(jié)點相連，K是偶數(shù)。相應(yīng)的AUC和Precision的結(jié)果如圖6所示。

本文同樣使用相應(yīng)的規(guī)則網(wǎng)絡(luò)構(gòu)造算法生成了10個規(guī)則網(wǎng)絡(luò)即最近鄰耦合網(wǎng)絡(luò)。其中每個節(jié)點都與它左右各K/2個鄰居點相連，這里K是一個偶數(shù)。本文設(shè)置K值分別為2，4，…，20，網(wǎng)絡(luò)的節(jié)點數(shù)N=1 000,網(wǎng)絡(luò)的特征信息如表4所示，從net1到net10，網(wǎng)絡(luò)由稀疏到稠密。相應(yīng)的AUC和Precision的結(jié)果如圖7所示。

Table 4 ParameterKand features of 10 regular networks表4 參數(shù)K和10個規(guī)則網(wǎng)絡(luò)的特征

Fig.5 Relationship between Precision andα圖5 Precision與參數(shù)α之間的關(guān)系

從圖6、圖7中可以看出，總體而言，無論在小世界網(wǎng)絡(luò)還是規(guī)則網(wǎng)絡(luò)中，本文提出的WFR算法與FR算法相比在網(wǎng)絡(luò)更為稠密的情況下，WFR算法效果要明顯優(yōu)于FR算法。而相對稠密的網(wǎng)絡(luò)具有局部群落特點的PWCS現(xiàn)象也更為明顯，因而WFR算法優(yōu)于FR算法。

4.3 算法時間復雜度分析

在基于共同鄰居的鏈路預(yù)測算法中，計算節(jié)點對的共同鄰居的時間復雜度為,表示網(wǎng)絡(luò)的平均度。AA、RA兩種算法與CN算法有著相同的計算過程，因此與CN算法的時間復雜度相同。FR、WFR算法預(yù)測過程與基于共同鄰居的其他算法的預(yù)測過程相同，即與CN、AA、RA算法的預(yù)測結(jié)果相同。如CN算法的時間復雜度為O(n2×k)。因此WFR-CN算法的時間復雜度為O(n2×k),保證了該算法的時間復雜度不大的情況下，取得了比CN、AA、RA、FR算法更優(yōu)的預(yù)測效果。

5 結(jié)束語

WFR算法是一種基于加權(quán)朋友推薦的鏈路預(yù)測算法，該算法利用社交網(wǎng)絡(luò)好友推薦策略，中介人傾向于將自己更熟悉的人介紹給目標用戶的特點，結(jié)合局部特征構(gòu)建節(jié)點相似性度量指標。WFR有效區(qū)分了用戶節(jié)點之間影響力的不同，更適用于具有局部群落結(jié)構(gòu)現(xiàn)象（PWCS）特征的網(wǎng)絡(luò)環(huán)境。與CN、AA、RA、FR這些基于共同鄰居的鏈路預(yù)測算法相比，WFR算法在保證時間復雜度大致相同的情況下，整體上取得了較好的預(yù)測效果。本文研究的鏈路預(yù)測算法主要考慮共同鄰居節(jié)點和局部結(jié)構(gòu)特征，對網(wǎng)絡(luò)的描述刻畫仍不夠全面。下一步的研究工作主要有兩方面：一是如何利用更多的網(wǎng)絡(luò)結(jié)構(gòu)信息來提高鏈路預(yù)測的效果；二是如何針對具有不同特征的網(wǎng)絡(luò)結(jié)構(gòu)提出合適的高效鏈路預(yù)測算法。

Fig.6 AUC and Precision of FR and WFR-CN in NW small world networks圖6 小世界網(wǎng)絡(luò)中AUC、Precision下的FR、WFR-CN指標

Fig.7 AUC and Precision of FR and WFR-CN in regular networks圖7 規(guī)則網(wǎng)絡(luò)中AUC、Precision下的FR、WFR-CN指標