基于仿水循環算法的梯級水庫群多目標優化調度研究

吳智丁

(大唐水電科學技術研究院有限公司，廣西 南寧 530025)

1 研究背景

我國水利資源豐富，如何綜合考慮灌溉、發電、防洪和供水等需求是梯級水庫群優化調度的核心問題，關系著社會、經濟和環境等多方面的綜合利益[1，2]。然而梯級水庫群之間存在著水文、水力、電力、經濟之間的強耦合關系，呈現多目標、非線性、變量多和約束強等特性[3-6]。傳統優化方法，如線性規劃、非線性規劃和動態規劃等，會面臨難以直接求解、無法保證全局最優及維數災等難題[7-11]，智能種群優化方法，如遺傳算法(Genetic Algorithm，GA)、粒子群算法(Particle Swarm Optimization，PSO)、蛛群算法和布谷鳥算法等，又存在收斂速度慢、收斂早熟和魯棒性差等問題[12-15]。因此，在梯級水庫群優化調度中嘗試引入新的優化算法，以實現收斂性能和計算速度的均衡仍然是學術界研究的熱點和難點。

仿水循環算法(Water Cycle-like Algorithm，WCA)是近些年來出現的一種新的智能種群優化算法[16-18]，它模擬大自然水循環及水流動的過程，利用相對重力機制令水滴粒子在解空間內搜尋目標函數的最優解。同時構建匯流、分流、滲流、蒸發降雨4個優化策略，其中：①匯流策略使多個鄰近水滴粒子匯聚為單個水滴，匯流后的水滴粒子質量變大，能有效提高搜索速度，令水滴迅速逼近最優解；②分流策略能防止單個水滴粒子質量過大而導致的收斂早熟，當水滴粒子大于限制值時，則分流為多個小水滴繼續進行搜索；③滲流策略判斷當水滴粒子相對重力較弱時分裂為多個細小水滴在當前位置周圍進行局部搜索，大幅提高算法尋優能力；④蒸發降雨策略令相對重力為零，即迭代停滯的早熟水滴粒子蒸發并脫離當前位置，之后隨機降雨至解空間內，令其重新參與搜索，有效解決水滴粒子早熟及陷入局部最優解的難題。基于以上迭代機制和搜索策略，使得WCA能按照當前的搜索情況自主改變水滴種群數量和水滴粒子質量，智能調配搜索資源，令算法自適應當前的計算需求。因此WCA真正實現了種群的智能化，搜索能力強、魯棒性高，已經被廣泛用于多個領域，成為近些年來智能種群算法的一個新亮點，然而目前這一算法尚未引入多目標水庫群優化調度中。

本文對仿水循環算法進行研究，基于Pareto存檔進化策略(Pareto Archived Evolution Scheme，PAES)，構建多目標尋優問題下的WCA改進重力迭代機制，提出多目標仿水循環算法(Multi-objective Water Cycle-like Algorithm，MWCA)，并將其應用于梯級水庫群多目標優化調度中。

2 梯級水庫群多目標優化調度數學模型

2.1 目標函數

梯級水庫群兼具發電任務及民生、航運、農業、工業等供水用途，因此其調度策略的制定應兼顧這兩方面的需求。本文構建梯級水庫站群發電量最大及供水量最大的多目標優化調度模型，即在綜合考慮各約束條件及給定調度期內各時段區間來水的情況下，盡可能最大化發電量以提高供電效益，同時最大化供水量以提升供水效益。

(1)發電量最大。在給定有限來水下應最大化出力，多承擔電網負荷，提高調度時段內發電量，達到減少火電出力和節能減排的目的。

(1)

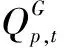
(2)供水量最大。供水量由農業灌溉供水量和工業、市政供水量組成，其中農業供水量主要來自河道區間引水，工業及市政供水量取自水庫庫區。提高流域及水庫群的整體供水量，有利于本調度期內梯級水庫群的供水效益和水能綜合利用。

(2)

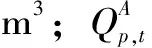
2.2 約束條件

(1)水量平衡約束。梯級水庫群間相互聯系緊密，上游水電站的出庫流量、棄水量，區間來水量、農業灌溉供水量，本級水電站的發電流量、市政供水量、棄水量等都對本級水電站的庫容和下游水電站的發電有較大影響，其關系表達式為

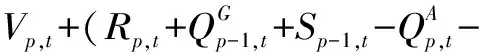
(3)

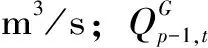
(2)農業供水流量約束。約束條件為

(4)

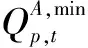
(3)工業及市政供水流量約束。約束條件為

(5)

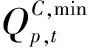
(4)蓄水量約束。約束條件為

(6)

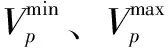
(5)發電流量約束。約束條件為

(7)

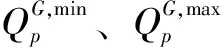
(6)發電出力約束。約束條件為

(8)

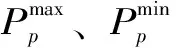
3 仿水循環算法

仿水循環算法(WCA)是從大自然水循環及水流動的現象中得到啟發提出一種全新的種群優化算法。算法首先隨機生成一組初始水滴，其對應的目標函數值為這些水滴的相對海拔高度，進而可以計算出其相對重力，水滴粒子在這相對重力的引導下進行迭代，相對重力較大的水滴粒子擁有更快的迭代速度。在迭代的過程中，WCA模擬水循環中匯流、分流、滲流、蒸發降水過程并構建相應的搜索策略，能根據當前水滴粒子的位置、質量、相對海拔等信息自動調整種群數量及水滴質量。例如在求解優化問題的初始階段，WCA能匯聚多個水滴粒子的力量集中對某個方向進行搜索，使得算法能較快逼近最優解附近，而在迭代后期，WCA利用分流滲流策略令水滴粒子進行細致的局部搜索。此外，蒸發降雨避免水滴粒子早熟而導致的資源浪費和搜索停滯。

3.1 重力尋優機制

假設最優求解問題為minf(x)，l≤x≤u，其中x為N維向量，上下界分別為l和u。WCA首先計算水滴種群對應的函數值，令其為水滴相對海拔高度。由物理原理可知，水流在重力的影響下從海拔較高處移動至海拔較低處。一般情況下，在優化問題中的最優值在計算前是未知的，因此WCA定義海拔高的水滴始終向著海拔低的水滴進行流動，即朝著當前更優的位置進行移動。此外，當出現多個低海拔水滴時，定義水滴i同時受到它們相對重力的牽引，構建其相對重力的合力為

(9)

式中，B為比水滴i更優的水滴集合；mi為水滴i的質量，初始質量為m0；k為當前迭代次數；f(xi)為水滴i對應的目標函數值。

為了提高水滴迭代的多樣性及可行性，在式(11)的基礎上加入隨機步長，WCA根據以下迭代方程確定水滴的新位置，即

(10)

式中，λg為隨機數，λg∈(0，1)。

3.2 匯流策略

在迭代過程中，通過計算水滴間的歐幾里得距離及相對海拔差，可對水滴在解空間的相對位置進行判斷，進而對位置接近的水滴群進行匯流操作。水滴i、j的歐氏距離計算公式和相對海拔差為

(11)

fd=|f(xi)-f(xj)|

(12)

式中，dij為水滴i、j間的歐氏距離；D為維數；fd為相對海拔。

(13)

xm=xi，best?i∈NM

(14)

式中，mi為參與匯流水滴的質量；NM為參與匯流的水滴數；mm為匯流后新水滴質量；xi，best為參與匯流的最優水滴位置；xm為匯流后新水滴的位置。

通過匯流策略，WCA能將相近的多個水滴匯聚為一個水滴，這樣不僅能增大單個水滴質量，集中搜索資源，加快水滴移動速度，并且還能有效減少水滴種群數量，加快迭代速度。

3.3 分流策略

為避免因匯流策略可能導致的水滴質量過大、種群大小銳減進而收斂早熟的問題，設定當水滴質量超過水滴初始質量的一定倍數時，分流其一半的質量形成一個新的水滴，并賦予新水滴粒子隨機的相對重力，即

ms=0.5mi

(15)

Fs=Fi+σsp

(16)

式中，mi為分流水滴的質量；ms為分流后新水滴的質量；Fi為分流水滴的相對重力；Fs為分流后新水滴的相對重力；σsp為N維隨機向量。

分流策略是對匯流策略的平衡，起到防止因質量過大造成的收斂早熟的作用，同時分流后隨機分布的新水滴也在一定程度上提高了種群多樣性。

3.4 滲流策略

模擬水對地表的滲透，構建WCA的滲流策略。在目前搜索到的最優解的臨近區域進行隨機搜索，探尋可能存在的最優值。其過程可簡單描述為依次對全局最優解各維數進行一維小范圍隨機擾動為

(17)

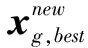
通過滲流策略，WCA能在當前全局最優解旁隨機探尋更好的解以替換當前解，該操作能有效提高算法的局部精細搜索能力，提高收斂精度。

3.5 蒸發降雨策略

在WCA迭代過程中，當前最優解xg，best是不斷進行更替的，處于xg，best中的水滴由于其相對海拔最低，不再受到其他水滴的相對重力影響，因此會造成搜索資源的浪費。WCA模擬自然界蒸發降雨過程，構建相應搜索策略，將處于相對海拔最低的水滴進行蒸發，按照初始質量m0平均分散為多個水滴并降雨至解空間的隨機位置中，重新展開迭代。即

NRF=mg，best/m0

(18)

xRF，i=l+λRF(u-l) ?i∈NRF

(19)

式中，mg，best為當前最優解的水滴質量；NRF為降雨后生產的水滴個數；λRF為隨機數，λRF∈(0，1)；xRF，i為降雨后各水滴的位置。WCA通過式(18)為得到降雨水滴個數，利用式(19)分配新水滴在解空間內的位置。

由于式(9)(10)的重力尋優機制中只需要當前最優解的位置而最優水滴本身并不參與計算，因此對其進行蒸發降雨操作并不影響算法正常迭代。蒸發降雨策略對處于當前最優的水滴進行處理，令其跳出當前位置，該操作能有效防止水滴陷入局部最優解，避免算法早熟，有效利用搜索資源，更能增加水滴多樣性，提高算法全局搜索性能。

4 多目標仿水循環算法(MWCA)

假設多目標優化問題可表達為

minf(x)=[f1(x)，f2(x)，…，fM(x)]

(20)

式中，f1(x)，…，fM(x)為多個目標函數；M為目標函數個數。對于此類多目標優化問題，其并不存在全局最優，因此對于WCA不存在唯一的最低海拔點。在此引入Pareto存檔進化策略(Pareto Archived Evolution Scheme，PAES)并進行一些改進，提出多目標仿水循環算法，將非劣解集(對應目標函數空間上的Pareto前沿)的點均認為是地形最低點，通過計算非劣解集中水滴的密度信息，令水滴有較大趨勢向著密度值較小的區域進行移動，改進后的多目標重力尋優機制可表示為

(21)

式中，NP表示位于非劣解集A的水滴數；ρfront，j為非劣解集內水滴j的密度信息；xfront，j為非劣解集內水滴j的位置；ffront，j為水滴j對應的Pareto前沿點。隨后，同樣利用式(10)進行水滴的移動。

經過此改進后，各水滴由原先的受到每一個低海拔水滴的吸引，轉變為受到非劣解集中所有水滴施加的相對重力。其中非劣解集中密度值低的水滴粒子施加的相對重力較大，密度值高的水滴產生的相對重力較小。改進后的尋優機制防止了水滴朝著單一非劣解移動導致水滴過于集中而陷于局部最優點，進而導致的收斂早熟問題，也避免了水滴被大量非劣解同時引導而致使的搜索緩慢現象。

針對帶約束的多目標優化問題，本文采用罰函數法進行處理，即對每一個目標函數加上約束條件的罰函數，則約束下優化問題即可轉變為無約束優化。MWCA的算法流程如圖1所示。

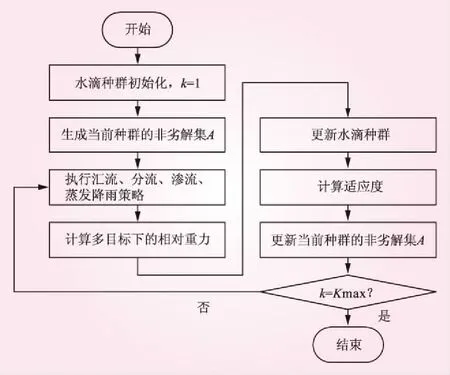
圖1 MWCA算法流程

具體步驟如下：

(1)初始化MWCA水滴種群，包括初始迭代次k=1、最大迭代次數Kmax、種群數量N、水滴群初始位置{x1，x2，…,xN}、初始適應度{f(x1)，f(x2)，…，f(xN)}和初始質量m0、根據PAES生成當前種群的非劣解集A。

(2)根據水滴質量和位置信息，執行匯流、分流、滲流、蒸發降雨策略，利用前文所述流程對水滴質量及水滴種群大小進行自適應調整和優化。

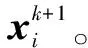
(5)更新水滴群的非劣解集解A，若A中所存儲的水滴數達到A的上限時，根據密度信息移除A中密度值最高的一個水滴，并將新水滴存入其中。

(6)重復步驟(2)～(5)，直至達到最大迭代次數，此時存于非劣解集A中的水滴位置就是多目標優化問題的最優解，其對于的適應度就是多目標優化值，列出或畫出相應的Pareto邊界，決策者就可通過不同的期望選擇相應的解。

5 實例應用

5.1 梯級水庫群實例

本文利用某流域梯級水庫群5個主要電站作為研究實例，其中1號電站為龍頭電站，5號電站為末端電站，農業灌溉供水從水庫上游的河道區間引水，工業及市政集中供水從各水庫中取水，調度期為一年，其中1月～3月為枯水期，6月～8月為豐水期，其他月份為平水期，各水庫及電站的裝機容量、額定庫容、正常水位等參數如表1所示。

表1 梯級水電站參數

表2 各算法非劣解及耗時對比

5.2 算法對比分析

為驗證MWCA算法的有效性與優越性，采用MOPSO算法[19]和NSGA-II算法[20]進行對比分析，對上述研究實例進行優化調度計算。仿真環境為配置i5-2520M、16G內存的聯想T420筆記本電腦，各算法分別獨立進行10次運算，其所有的非劣解在目標函數空間所對應的Pareto邊界如圖2所示。由圖2可知，3個算法的都具有較好的收斂穩定性，但MWCA所得非劣解的Pareto邊界分布更廣、更均勻。尤其是在年均發電量大于300億kW·h的區域內，MWCA搜索到了大量的非劣集，而MOPSO和NSGA-II在這一區域僅得到少數的解。此外，整體Pareto邊界也比另兩個算法更優，例如圖2中當年均發電量為240億kW·h時，MWCA非劣解的調度策略能提供116.5億m3的年均供水量，而MOPSO與NSGA-II僅能提供約116億m3的供水量，相比MWCA減少了0.5億m3。另一方面，當年均供水量為117億m3的時候，MWCA可獲得約210億kW·h的年均發電量，與之相比MOPSO與NSGA-II的發電量僅180億kW·h左右。這說明在同等求解目標及約束函數下，MWCA能在各個目標下均獲得比NSGA-II算法與MOPSO算法更好的求解性能和更優的非劣解。這得益于MWCA的滲流與蒸發降雨策略，有效的提高了水滴種群的多樣性，同樣也增強了MWCA的局部尋優性能，使其獲得了更多的非劣解。各算法10次獨立計算的多目標優化結果最大值、最小值、非劣解數量、耗時等如表2所示。

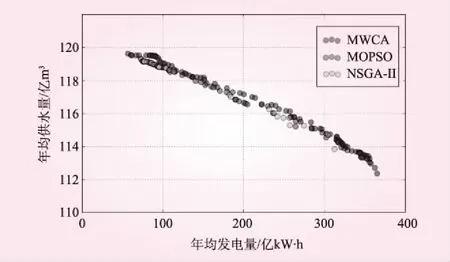
圖2 各算法獨立10次運算后所得的Pareto邊界

由表2可知，MWCA所得到的調度策略能獲得最高367.16億kW·h的年均發電量，相比MOPSO的358.41億kW·h和NSGA-II的313.15億kW·h分別多出了8.75億kW·h和54.01億kW·h的發電量。同時MWCA所得的最大年供水量119.64億m3也比MOPSO和NSGA-II的多出了0.58億m3和0.32億m3。此外，MWCA所得非劣解的年均最小年均發電量比NSGA-II與MOPSO更小。這表明MWCA所獲得的非劣解范圍更廣，搜索性能更強。經過10次獨立運算后，MWCA能獲得84個非劣解，與此同時MOPSO與NSGA-II僅分別獲得51個和48個非劣解。在計算耗時上，MWCA、MOPSO和NSGA-II平均為11.07、9.82 s和11.50 s。雖然MWCA耗時并非最少，但利用相近的時間，MWCA獲得了多于另兩個算法的非劣解數量，體現了該算法在迭代速度和和性能上的優越性。

為進一步分析算法所得非劣解的分布特性，本文采用分布距離指標(SD)[19]及超體積指標(HV)[21]進行高階評價。其中分布距離指標用于分析非劣解分布的均勻性，其計算式為

(22)

式中，ds，i為非劣解兩兩間的距離，ds，i=minj|f1(xi)-f1(xj)+f2(xi)-f2(xj)|，i，j=1，2，…，nnd；ds，avg為ds，i的平均值；nnd為所得非劣解的數量。該值越小，則所有非劣解兩兩間的距離越一致，即實現非劣解的平均分布。本文算例中3個算法的SP值如表3所示。

表3 各算法非劣解及耗時對比

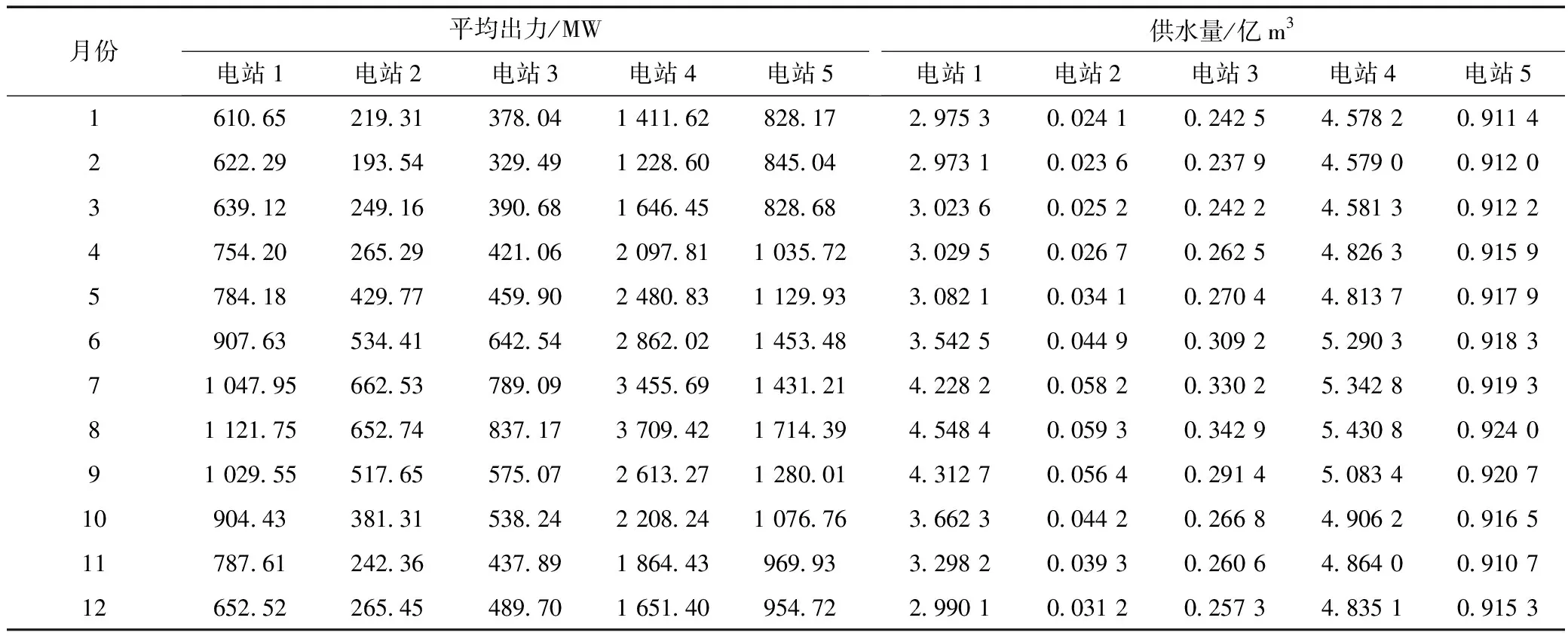
表4 MWCA優化調度結果

可見MWCA算法所得非劣解的分布距離指標為9.528 5，遠小于MOPSO算法和NSGA-II算法，說明了MWCA非劣解的分布更為平均。此外MWCA較小的平均距離也同樣證明了這點。

超體積指標利用非劣解在多目標函數空間上所圍成的超空間體積(面積)作為評判標準，本算例三個算法所得非劣解的超體積示意及數據如圖3所示。由圖3可知，MWCA算法所得超體積指標為199.63，明顯大于MOPSO算法的132.84及NSGA-II算法的99.67。通過分布距離指標和超體積指標的高階分析，MWCA同樣顯示出了優于另兩個算法的均勻性和寬廣性，這再次驗證了本文算法優越的多目標優化性能。

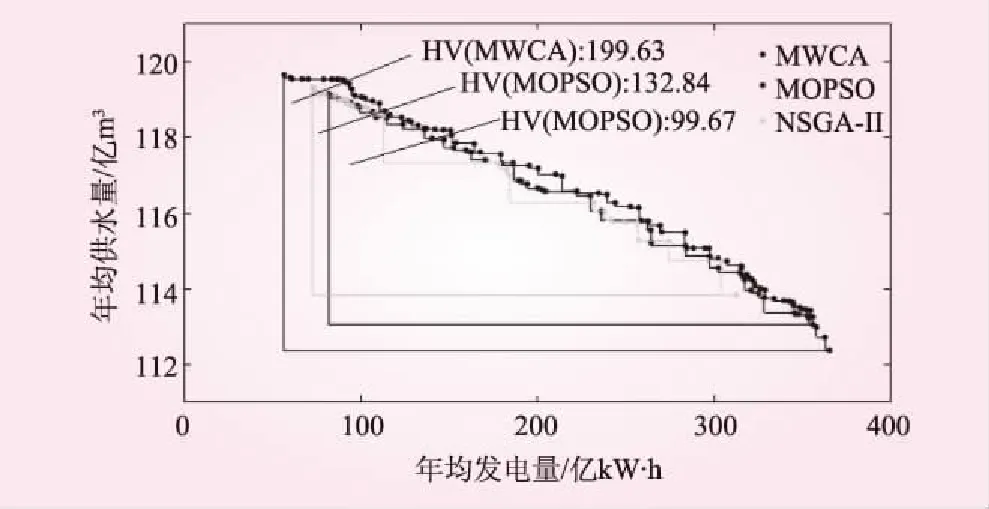
圖3 各算法的超體積指標(HV)示意

5.3 MWCA調度結果分析

由于處于Pareto邊界的非劣解均為多目標優化問題的有效解，對非劣解的選擇取決于決策者的調度策略偏好，有的希望提高發電量，而有的希望增加供水量。本文不對調度策略的偏好進行研究，因此選取發電量與供水量較為均衡的一組非劣解進行分析，如表4所示。

由表4可知，各電站的出力與枯水期和豐水期的趨勢一致，在來水較少的1月～3月，各電站平均出力都比6月～8月低。在供水量方面，不論在枯水期還是豐水期，MWCA所得非劣解給出的調度策略都能保證較好的供水量，即使在枯水期的1月～3月，各水庫及其上游河道區間仍保持了較好的供水能力。相較平均出力的較大變化，供水量的浮動并不大，這一方面是由于水庫群的蓄水功能保證了一定的供水量，另一方面則是通過降低水電站出力進行了一定妥協。在枯水期的情況下，削減水電站出力，保證最低供水量及死水位約束。此外，這也體現了“蓄豐補枯”的補水調度作用，在豐水期來臨之時多蓄水，便能在枯水期到來時提供足夠的供水量滿足工業和民生需求。上述調度策略顯示了MWCA應用于梯級水庫群優化調度的合理性與有效性。

6 結 論

本文針對梯級水庫群調度問題，構建了發電量最大和供水量最大的多目標優化調度模型，提出了多目標仿水循環算法MWCA，引入了匯流、分流、滲流、蒸發降雨4個優化策略對水滴種群進行處理，能有效提高種群多樣性、提升搜索性能、加快收斂速度、防止陷入局部最優、避免迭代早熟等，針對多目標優化問題，構建了新的重力迭代和尋優機制。實例應用結果驗證了MWCA在水庫群多目標優化調度問題中的合理性和可行性，同時也表明了MWCA相比MOPSO和NSGA-II的搜索性能更強，非劣解多樣性更好、分布更均勻和寬廣，具有較好的研究和工程應用前景，為梯級水庫群多目標優化調度問題提供了一種有效的解決方案。