隨機振動激勵下的壓電俘能器發電性能模擬與分析*
王紅艷,苗鳳娟,孫志龍,荊麗秋
(1.齊齊哈爾大學機電工程學院,黑龍江 齊齊哈爾 161006;2.齊齊哈爾大學通信與電子工程學院,黑龍江 齊齊哈爾 161006)
隨著微電子技術的迅猛發展,傳統以化學電池為主供能方式的弊端也逐漸顯露出來,如體積大、使用壽命短、特殊場合難于更換等。可替代能源的研究引起了人們的關注。振動是一種自然界普遍存在的物理現象,不僅聲、光、熱現象中包含振動,它還以機械運動的形式廣泛存在,如橋梁和建筑物在陣風或地震激勵下的振動,汽車在崎嶇不平道路上行使時的振動,機床和刀具在加工過程中的振動等。振動能可以轉換為電能用于為微電子產品供能。振動能向電能的轉換方式主要有壓電式[1-3]、電磁式[4]、靜電式[5]和摩電式[6]4種。其中,壓電式換能結構以體積小、功率密度高、易于集成化等優點成為當前研究的熱點。
以往對壓電俘能器發電性能的研究多采用簡諧激勵的方式[7-10],這種激勵方式與實際環境振動源隨機性和多樣性特點不相符合。為了研究壓電俘能器在實際環境中的發電性能,本文以路面不平度引起的車體隨機振動作為激勵源,研究壓電俘能器在隨機振動激勵條件下的發電性能。首先建立路面-車輛系統垂向振動模型,通過引入路面不平度時域模型,分析車體振動時域響應。然后將車體響應作用于壓電俘能器上,通過有限元方法分析壓電振子的模態頻率及外接負載對其發電性能的影響。獲得的最優負載被用于提取不同車速和路面不平度條件下壓電俘能器的輸出功率,以此研究車速和路面不平度對系統發電性能的影響。
1 路面-車輛系統垂向振動分析
假設車輛前、后軸垂直方向的運動相互獨立,將整車模型簡化成一個兩自由度1/4車輛系統,如圖1所示。圖1中,m1為車輪質量,k1為輪胎剛度,m2為車體質量,k2為懸架剛度,c為懸架阻尼系數。v為車輛在水平方向的運動速度。q(t)為路面不平度位移輸入,u1(t)和u2(t)分別為車輪和車體的垂向方向運動位移。
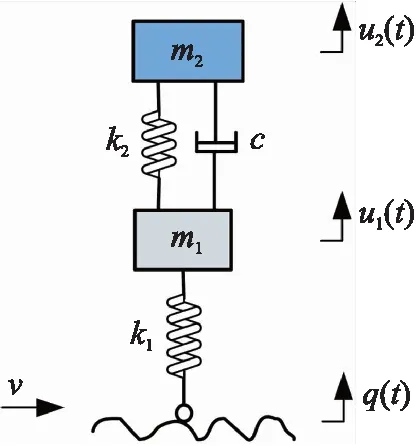
圖1 兩自由度1/4車輛系統
對圖1中的兩自由度1/4車輛系統進行數學建模,得到
(1)
式中:
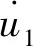
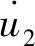
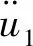
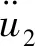
定義狀態空間矢量
(2)
(3)
u=q
(4)
式(2)中,矢量x對時間求導得到,
(5)
合并整理式(1)~式(5),建立路面-車輛系統狀態空間方程,
(6)
式中:
D=[0 0 0]T
根據文獻[11],基于有理函數的路面不平度時域模型可表達為
(7)
式中:w0(t)為協方差為1 m2/s的單位白噪聲。Gq(n0)為路面不平度系數。其中,n0為參考空間頻率,n0=0.1 m-1。路面不平度共有8級分類標準(A、B、C、D、E、F、G、H),對應的Gq(n0)分別為16,64,256,1 024,4 096,16 384,65 536,262 144[12],單位為10-6m3。
2 路面-車輛系統垂向振動仿真模擬

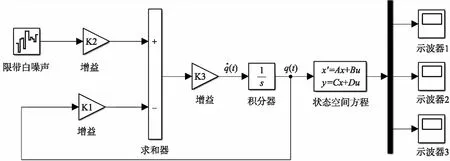
圖2 路面-車輛系統垂向振動時域仿真MATLAB/Simulink模型
設置車速v=10 m/s,Gq(n0)=64×10-6m3。圖3(a)、3(b)和3(c)所示分別為車輛在B級路面上行駛時,車體垂向振動位移、速度和加速度的時域響應圖。從圖3(a)、3(b)和3(c)中可以看出,車體垂向振動的位移、速度和加速度響應具有隨機性。

圖3 車體垂向振動位移、速度和加速度瞬態響應(v=10 m/s)
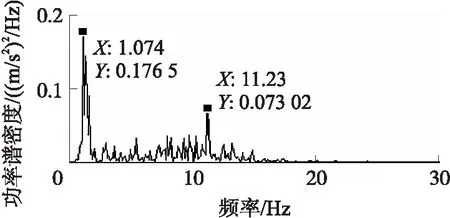
圖4 車體垂向加速度的功率譜圖(v=10 m/s)
圖4所示為車體加速度功率譜圖。從圖4中可以看出,車體在兩個頻率(1.074 Hz和11.23 Hz)存在功率譜密度峰值。本文在第4部分將對安裝在車體上的壓電梁進行結構設計和發電性能研究。考慮到梁結構壓電俘能器固有頻率很難達到1.074 Hz,本文設計壓電俘能器時以11.23 Hz作為參考頻率。
3 壓電俘能器結構及電性能分析
3.1 壓電俘能結構
圖5所示為壓電雙晶梁結構示意圖。壓電梁為三層結構,中間層為金屬層,上下表面分別粘貼壓電片,壓電片采用d31模式,兩個壓電片串聯連接后為負載供能。金屬層長度L=66 mm,寬度w=20 mm,厚度hm=0.3 mm。壓電層與金屬層長、寬相等。單個壓電層厚度hp=0.2 mm。壓電梁末端質量Mt=0.09 kg。壓電梁所受激振力來自于車體的垂向運動。
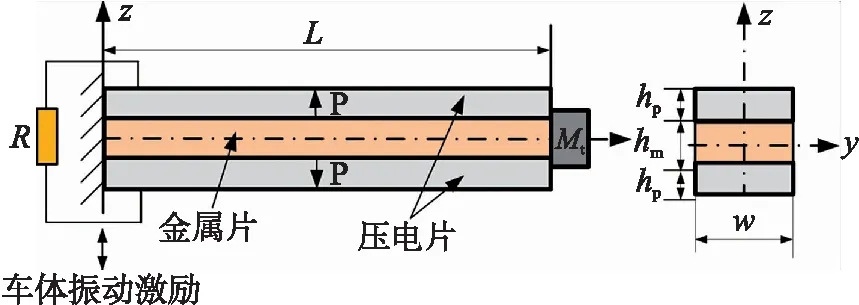
圖5 壓電雙晶梁結構示意圖
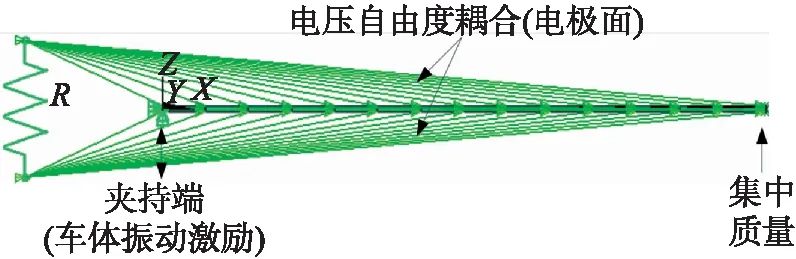
圖6 壓電雙晶梁有限元模型
3.2 有限元模型
圖6所示為在ANSYS軟件中建立的壓電雙晶梁有限元仿真模型。按3.1節給出的壓電俘能器結構尺寸建立實體模型。金屬層定義材料參數如下:密度8 920 kg/m3,彈性模量106 GPa,泊松比0.35。壓電層材料為PZT5H,其各項異性參數(彈性柔順矩陣、壓電常數矩陣、介電常數矩陣)詳見文獻[13]。注意將兩個壓電層設置成極化方向相反(壓電常數符號不同),以保證兩個壓電片串聯連接。金屬層采用 solid45單元,壓電層采用solid5 單元,電阻采用circu94單元。末端質量Mt采用集中質量的形式施加,單元號為mass21。網格劃分形式為自由網格劃分。壓電梁中間兩個電極面上各點電壓耦合連接,底層電極面與負載電阻一端耦合連接,電壓定義為零。頂層電極面與負載另一端耦合相連,輸出電壓、電流和功率。有限元瞬態分析使用的瑞利阻尼系數由下式計算得到
(8)
式中:α為質量阻尼系數,β為剛度阻尼系數。ω1和ω2分別為壓電雙晶梁一階和二階彎振圓頻率,ω1=2πf1,ω2=2πf2。其中,f1和f2分別為一階和二階彎振頻率。ζ1和ζ2分別為壓電雙晶梁一階和二階彎振模態對應的阻尼比。有限元分析內容包括3個方面:其一是壓電梁固有頻率與激勵頻率的匹配關系對發電量的影響;其二是負載電阻對發電量的影響:其三是車速和路面不平度系數對系統發電量的影響。
3.3 分析結果
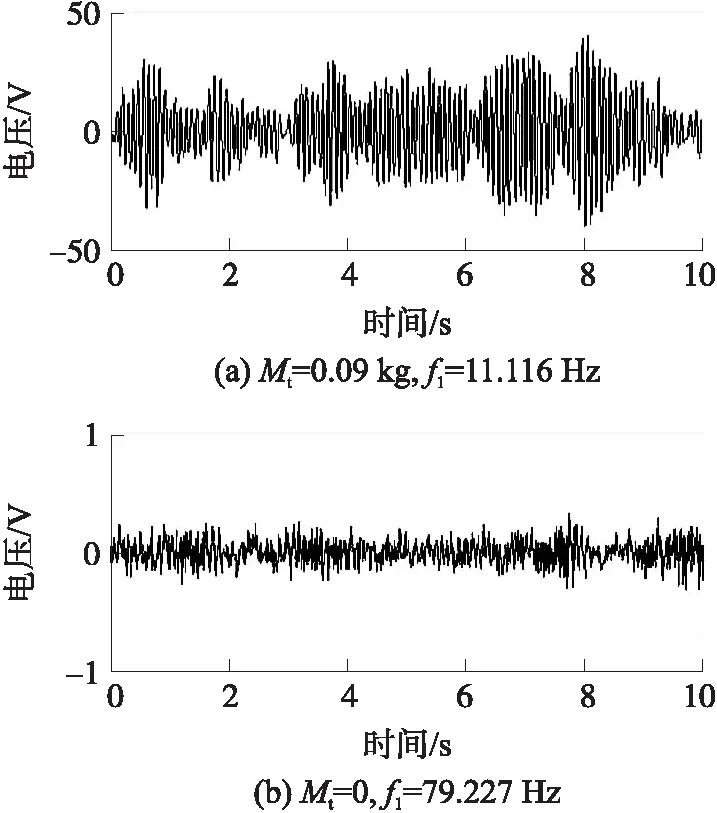
為了研究壓電梁的模態頻率與激勵頻率的匹配關系對系統發電性能的影響,我們對兩種不同基頻的壓電俘能器進行了發電能力比較研究。一個壓電梁上施加末端質量(Mt=0.09 kg),另一個壓電梁上不施加末端質量(Mt=0)。有限元模態分析得到兩種配置的壓電梁一階模態頻率分別為11.116 Hz(該頻率接近于車輛系統固有頻率11.23 Hz)和79.227 Hz。連接1 MΩ的負載電阻進行電學量諧響應分析。需要注意的是兩個不同結構的瑞利阻尼系數需各自計算給出。以Mt=0.09 kg配置為例,壓電梁前兩階模態頻率f1=11.116 Hz,f2=341.66 Hz。取ζ1=ζ2=0.02,根據式(8)計算得到瑞利阻尼系數α=1.352 9,β=9.023 0e-6。圖7(a)和7(b)所示分別為末端質量Mt=0.09 kg和Mt=0時的壓電俘能器輸出電壓隨時間變化圖。對比圖7(a)和7(b)可以看出,相比于模態頻率f1=79.227 Hz的壓電梁(Mt=0),模態頻率f1=11.116 Hz的壓電梁(Mt=0.09 kg)具有更高的輸出電壓。由此可見,當壓電梁固有頻率匹配車輛系統固有頻率時,系統會獲得更高的輸出電壓。
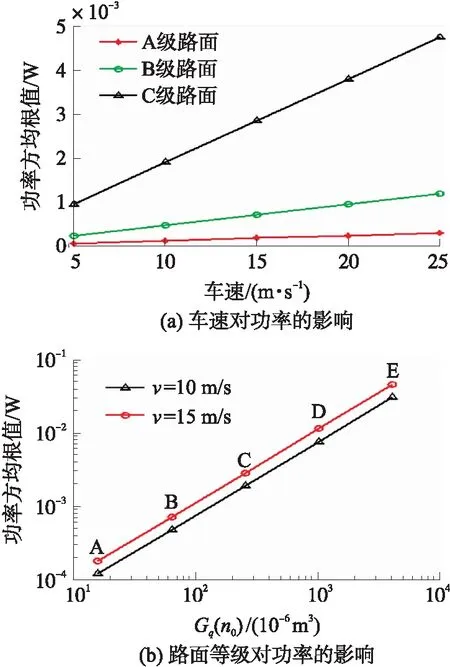
設置壓電梁末端質量Mt=0.09 kg,響應時間10 s,配置不同的負載電阻,分析負載電阻對壓電俘能器輸出電量的影響關系。對電壓、電流和功率瞬態響應值求取方均根值,得到壓電俘能器方均根電壓、電流和功率隨負載電阻變化曲線圖,如圖8(a)~8(c)所示。從圖8(a)~8(c)中可以看出,在相同路面等級條件下,隨著負載電阻阻值的增大,壓電俘能器輸出電壓逐漸增加、輸出電流逐漸減小,存在最優負載(約為200 kΩ)使壓電俘能器的輸出功率達到最大。對于同一負載電阻,路面不平度系數越大(A級 圖8 負載電阻對壓電俘能器輸出電壓、電流和功率的影響關系圖(v=10 m/s) 圖7 壓電俘能器輸出電壓隨時間變化圖(v=10 m/s,R=1 MΩ) 從路面-車輛系統垂向振動時域仿真MATLAB/Simulink模型(見圖2)可以看出,除車輛系統自身參數外,影響車體垂向運動位移的因素還有兩個,即車輛運動速度v和路面不平度系數Gq(n0)。連接最優負載電阻R=200 kΩ到壓電俘能器上。圖9(a)和9(b)所示分別為車體速度和路面等級對壓電俘能器方均根功率的影響關系圖。從圖9(a)中可以看出,在同一路面等級條件下,壓電俘能器輸出功率隨車速增加呈現線性增加的趨勢。從圖9(b)中可以看出,同一車速條件下,隨著路面不平度系數的增加(A級 圖9 車速和路面等級對輸出功率的影響(R=200 kΩ) 本文以兩自由度1/4車輛模型為載體對隨機振動激勵下的壓電俘能器發電性能進行了研究。建立了路面-車輛系統垂向振動模型,通過引入路面不平度時域模型,利用MATLAB/Simulink軟件進行了路面-車輛系統垂向振動仿真,車體垂向位移作為激勵源作用于壓電俘能器上使其發電,得到結論如下:① 當壓電俘能器固有頻率匹配車輛系統固有頻率(11.23 Hz)時,壓電俘能器可以獲得更高的輸出電壓。② 隨著壓電俘能器外接負載電阻值的增加,壓電俘能器輸出電壓逐漸增大、輸出電流逐漸減小,存在最優負載(約為200 kΩ)使壓電俘能器輸出功率達到最大。③ 連接最優負載電阻,路面不平度等級相同時,隨著車輛速度的增加,壓電俘能器輸出功率逐漸增大;車速相同時,隨著路面不平度系數的增加,壓電俘能器輸出功率逐漸增大。車速10 m/s時,行駛在B級路面上的車體可激勵壓電俘能器產生最大功率約為0.5 mW。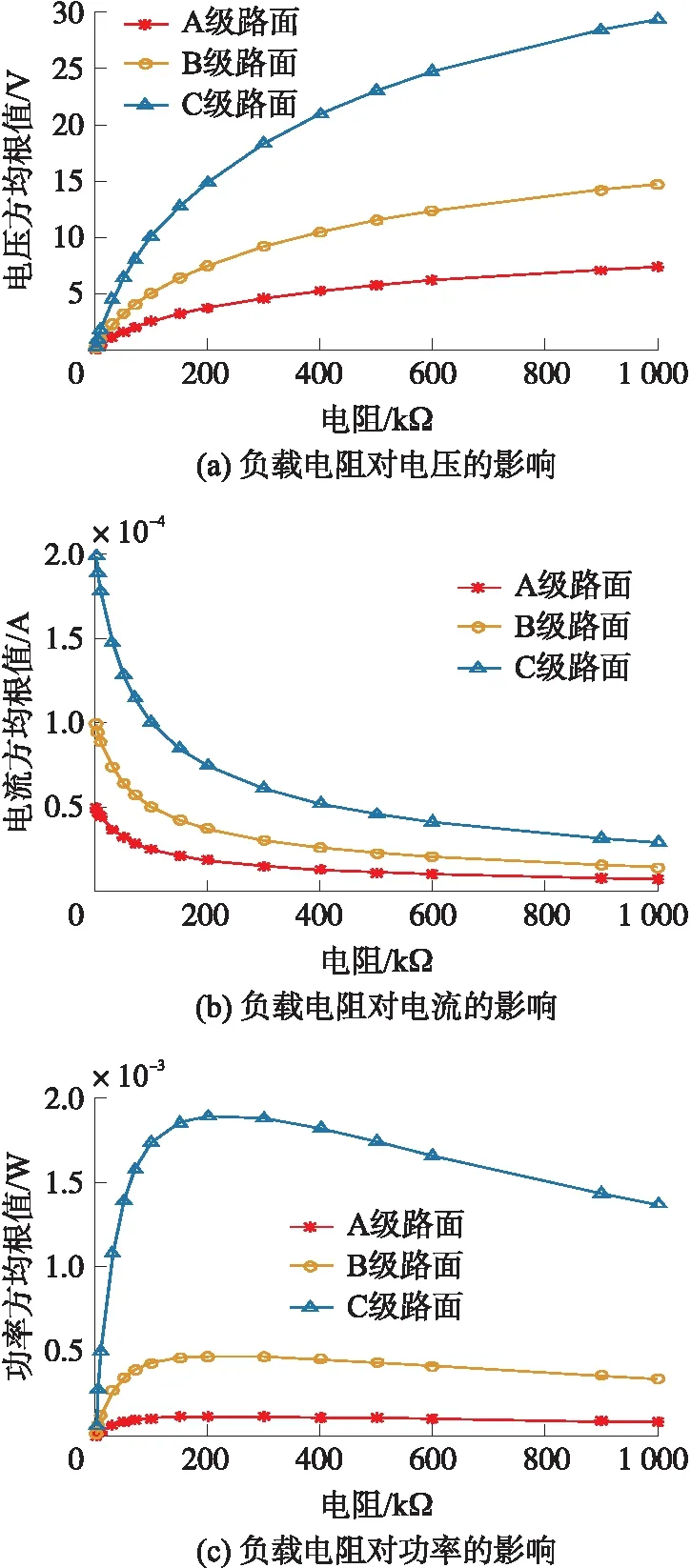
4 結論

