基于CPML-RML組合邊界條件粘彈TTI介質旋轉交錯網格有限差分正演模擬

張奎濤,顧漢明,劉少勇,劉春成,陳寶書,張 立,肖逸飛

(1.中國地質大學(武漢)地球物理與空間信息學院,地球內部多尺度成像湖北省重點實驗室,湖北武漢430074;2.中海油研究總院有限責任公司,北京100028)

實際地下介質中充滿流體、裂縫與裂隙,會同時表現出各向異性與粘彈性特征,對地震波的振幅和相位造成影響,因此,在進行地震波場數值模擬時,這種粘滯性特征不能忽視。粘彈各向異性現象在實驗室與波場測量中得到了證實[1]。

對于粘彈各向異性介質,國內外學者進行了大量的研究。CARCIONE[2-3]基于廣義標準線性固體(GSLS)模型,建立了線性粘彈性各向異性本構關系及相應的波動方程,為后續在粘彈性各向異性介質中的應用進行了大量的研究[4-7]。受制于實際計算和存儲能力,地震數值模擬通常僅能在有限空間進行,因此,需要在計算區域周圍增加人工邊界條件以降低邊界反射干擾。完全匹配層(PML)吸收邊界條件是一種典型的人工邊界條件,由于其穩健和高效的吸收特性而被廣泛使用[8-12]。它由BERENGER[13]于1994年提出,之后許多學者在其基礎上加以改進,使其變得更加高效。其中最具代表性的是RODEN等[14]提出的卷積完全匹配層(CPML)吸收邊界條件,由于增加了額外的控制參數(α),其對低頻反射與掠射波有較好的吸收效果。隨后,許多學者將CPML吸收邊界條件應用到一階速度-應力方程的數值模擬中,并取得了較滿意的效果[15-18]。LI等[19]在CPML吸收邊界條件中引入了輔助記憶變量,避免了卷積操作并將其成功應用到二階波動方程數值模擬中。WANG等[20]使用CPML吸收邊界條件對分數時間導數的粘聲波方程進行了數值模擬。然而,傳統的PML吸收邊界條件在大炮檢距掠射情況下吸收效果不理想,對于某些介質存在不穩定性[21],而CPML吸收邊界條件在復雜介質構造情況下,對低頻反射的吸收效果不佳,干擾了有效波。另一類人工邊界條件是隨機介質層(RML)邊界條件。RML最早由CLAPP[22]提出,隨后有學者將其應用于逆時偏移中[23-24],方法是在邊界區域設置隨機介質,使得波場傳播到邊界區域時發生不相干散射,削弱邊界反射的能量,達到減少人工邊界反射干擾的目的。

有許多不同的網格被應用于有限差分正演模擬中[25-27]。其中最為經典并應用最廣泛的是標準交錯網格(stand-staggered-grid,SSG)。SSG由MADARIAGA[28]在研究斷層破碎時所提出,隨后被廣泛應用于有限差分數值模擬中[29-31]。交錯網格是將彈性參數定義在整網格點或半網格點上,對于包含多參數模型的數值模擬,在計算某些量的空間導數時,存在所需模型參數在相應空間節點沒有定義的問題,需要對模型空間進行插值或近似處理。這些模型空間的處理會引入計算誤差,在模型參數變化較為劇烈區域甚至會出現數值計算不穩定現象。為了解決SSG在多參數模型數值模擬中存在的問題,SAENGER等[32-33]提出了旋轉交錯網格(rotated-staggered-grid,RSG)算法,因其將彈性參數定義在整網格點或網格中心上,在計算空間導數時無需進行插值處理,從而避免了插值處理帶來的計算誤差,提高了數值模擬的精度。此外,由于RSG是利用網格對角線上的信息來求解空間導數,因此比SSG更加穩定,得到的數值解更加可靠。由于RSG具有較好的穩定性,被眾多學者應用于各種復雜介質的數值模擬中[34-36]。

本文在前人研究的基礎上,采用基于GSLS模型的粘彈TTI介質波動方程進行數值模擬。在邊界處理上,利用隨機邊界的散射特點進一步改善CPML吸收邊界條件的吸收能力,提出將CPML吸收邊界條件與RML邊界條件相結合的策略,并推導出相應的旋轉交錯網格有限差分格式,利用均勻介質模型及復雜介質Hess模型對組合邊界條件的正確性及有效性進行了測試及對比分析。

1 理論與方法

1.1 粘彈TTI介質波動方程

根據CARCIONE[2-3]基于GSLS模型建立的線性粘彈性各向異性理論,可得到粘彈TTI介質波動方程。

應力-應變關系:

(1)

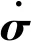
(2)

其中,K為廣義非壓縮模量,G為廣義剛性模量,cij為彈性系數,eij為記憶變量分量。

記憶變量方程為:

(3)

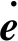
式中:Qv(v=1,2)分別為縱、橫波品質因子;f0為地震子波主頻。

(5)

其中,

速度與應力關系可用動量守恒方程表示:

(6)

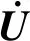
(7)

1.2 常規SPML吸收邊界條件

本文考慮二維情況,在復數伸展坐標下,(6)式可以寫成如下形式[38]:

(8)

(9)

對(9)式求偏導,有:

(10)

式中:sx,sz為復頻伸展函數。

(11)

將(10)式與(11)式代入(8)式,并在x,z方向分裂有:

將(12)式變換到時間域便可得到SPML吸收邊界條件[18],即

1.3 CPML吸收邊界條件

以(6)式為例(忽略外力),推導出適用于粘彈TTI介質的二維CPML吸收邊界條件。對于CPML吸收邊界條件,引入了兩個額外的衰減參數κ和α,使得新的復頻伸展函數變為:

(14)

式中:κi,αi為輔助衰減系數,且κi和αi滿足κi≥1,αi≥0,i=x,z。

整理(14)式得到:

(15)

將(10)式與(15)式代入(8)式中的第1個方程(以第1個方程為例,后面類似)有:

(16)

令

(17)

則(16)式可寫成:

(18)

整理(17)式得到:

本次共入選受試者236例，其中試驗組脫落9例、對照組脫落6例。最終208例患者進入符合方案數據集（PPS），221例患者進入全分析數據集（FAS），231例患者進入安全性數據集（SS）。全部病例均簽署知情同意書。

(19)

將(19)式變換到時間域,有:

(20)

不失一般性地,對于方程

(21)

其通解為:

(22)

(22)式在時間域離散形式下有:

(23)

即有:

(24)

對比(22)式,(18)式的解為:

(25)

式中:

(26)

i=x,z

則(18)式在時間域的形式為:

(27)

式中:Txx,Txz可采用(25)式迭代求解得到。對比(6)式中vx分量項與(27)式可以發現,只需將?i替換成?i/κi+Tij(i,j=x,z)即可得到相應的粘彈TTI介質的CPML吸收邊界條件。

1.4 CPML-RML組合邊界條件

一般而言,對于單一隨機邊界條件,由于隨機邊界區域填充的為隨機介質,可被認為由一個個散射點組成,當波場傳播到該區域時,波場發生隨機散射形成非相干能量,從而達到減少人工邊界反射的目的。然而,由于散射方向是任意的,因此,還是有部分較強的能量會被散射到有效物理計算區域,從而污染了原有的地震波場;另一方面,在某些大角度入射的情況下,CPML吸收邊界條件對低頻反射及掠射波的吸收能力有限,可采用隨機介質將其能量散射。因此,本文利用隨機介質層(RML)邊界的散射特點,提出CPML吸收邊界條件與RML邊界條件相組合的策略,進一步提升邊界的吸收效果。

圖1為CPML-RML組合邊界示意圖。其中,隨機邊界區域填充的隨機介質可采用隨機介質建模得到。在具體實施過程中,根據隨機介質建模理論公式,給定自相關長度(分散程度)、相關半徑、方向角度和方差等隨機介質建模參數,然后將計算區域的彈性參數取均值作為隨機邊界區域彈性參數的背景值,最后采用隨機介質建模程序得到隨機彈性參數,并將其賦值在隨機邊界區域的每個網格點處,其中隨機邊界區域的彈性參數滿足其均值為背景值,方差為給定的方差。因此,當波場傳播到邊界時,首先會進入CPML邊界區域進行吸收衰減,然后會進入隨機邊界區域,能量會被散射,使得最終的人工邊界反射被極大地衰減,從而達到非常好的吸收效果。

圖1 CPML-RML組合邊界示意圖解

1.5 旋轉交錯網格有限差分格式

旋轉交錯網格(RSG)的基本思想是將彈性參數定義在整網格點或網格中心點上,如圖2所示。

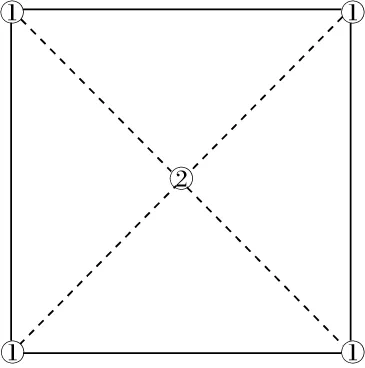
圖2 旋轉交錯網格示意圖解

在網格點①處存放vi、ρ,在網格點②處存放σij、eij、cij,然后在對角線方向上計算相應量的空間導數,此過程中避免了插值操作,使得編程實現更簡單,正演模擬的精度和穩定性更高。其計算公式為:

(28a)

(28b)

式中:i,j,n分別為x,z,t方向樣點序號;u為速度波場或應力波場;Lx,Lz分別為x,z方向上的微分算子;Δx,Δz分別為x,z方向上的空間離散步長;N為差分階數的1/2;m為差分階數序號;cm為差分系數,可采用Taylor展開推導得到。

二維情況下的粘彈TTI介質波動方程CPML吸收邊界條件旋轉交錯網格有限差分格式為:

(29a)

(29b)

(30a)

(30b)

(30c)

(31a)

(31b)

(31c)

(32)

式中:u為速度波場或應力波場;Δt為時間步長。

2 數值模擬與分析

2.1 二維均勻介質模型

為了對比SPML吸收邊界條件、CPML吸收邊界條件與CPML-RML組合邊界條件的吸收效果,本文設計了一個大小為2500m×500m的均勻介質模型,網格間距為5m×5m,時間步長為1ms,總時間采樣點數為2000,共2s記錄長度,采用30Hz主頻的雷克子波,空間差分階數為20階,邊界層厚度為250m(對于組合邊界,CPML和RML邊界厚度各125m),震源的位置為(750m,150m),接收排列范圍為0～2500m,排列深度為150m,接收點間距為10m,共251道接收,其均勻介質彈性參數見表1。

圖3、圖4和圖5分別給出了SPML吸收邊界條件、CPML吸收邊界條件和CPML-RML組合邊界條件的x分量地震記錄及波場快照。波場快照從上到下對應的時間依次為0.4s、0.6s和1.0s,并且為了區分對比,地震記錄及波場快照均做了增益處理,使其振幅處于同一水平范圍,即在制圖過程中,將所有數據的振幅統一限制在某一更低(相比于原始數據范圍)的數值范圍內(例如將所有波場快照數據的振幅限制在-0.2～0.2),這樣既能達到增益效果,又能實現振幅對比。從圖3、圖4和圖5中可以看出,在0.6s之前,不論采用哪種邊界條件,其吸收效果均很好,未看見明顯的邊界反射,說明3種吸收邊界條件在波場傳播的前期均有好的吸收效果。但值得注意的是,當波場傳播到后期(1.0s),即波場大角度入射到邊界時,SPML吸收邊界條件會出現如紅色箭頭所示的邊界反射,即SPML吸收邊界條件不能很好地將大角度的邊界反射吸收;而CPML吸收邊界條件會出現弱邊界反射,但其效果優于SPML吸收邊界條件;CPML-RML組合邊界條件從地震記錄及波場快照上均未出現邊界反射。說明與SPML吸收邊界條件和CPML吸收邊界條件相比,本文提出的CPML-RML組合邊界條件在吸收人工邊界反射方面更加優越。

表1 粘彈TTI均勻介質彈性參數

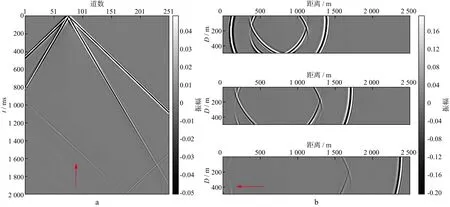
圖3 SPML吸收邊界條件的x分量地震記錄(a)與波場快照(b)

圖4 CPML吸收邊界條件的x分量地震記錄(a)與波場快照(b)

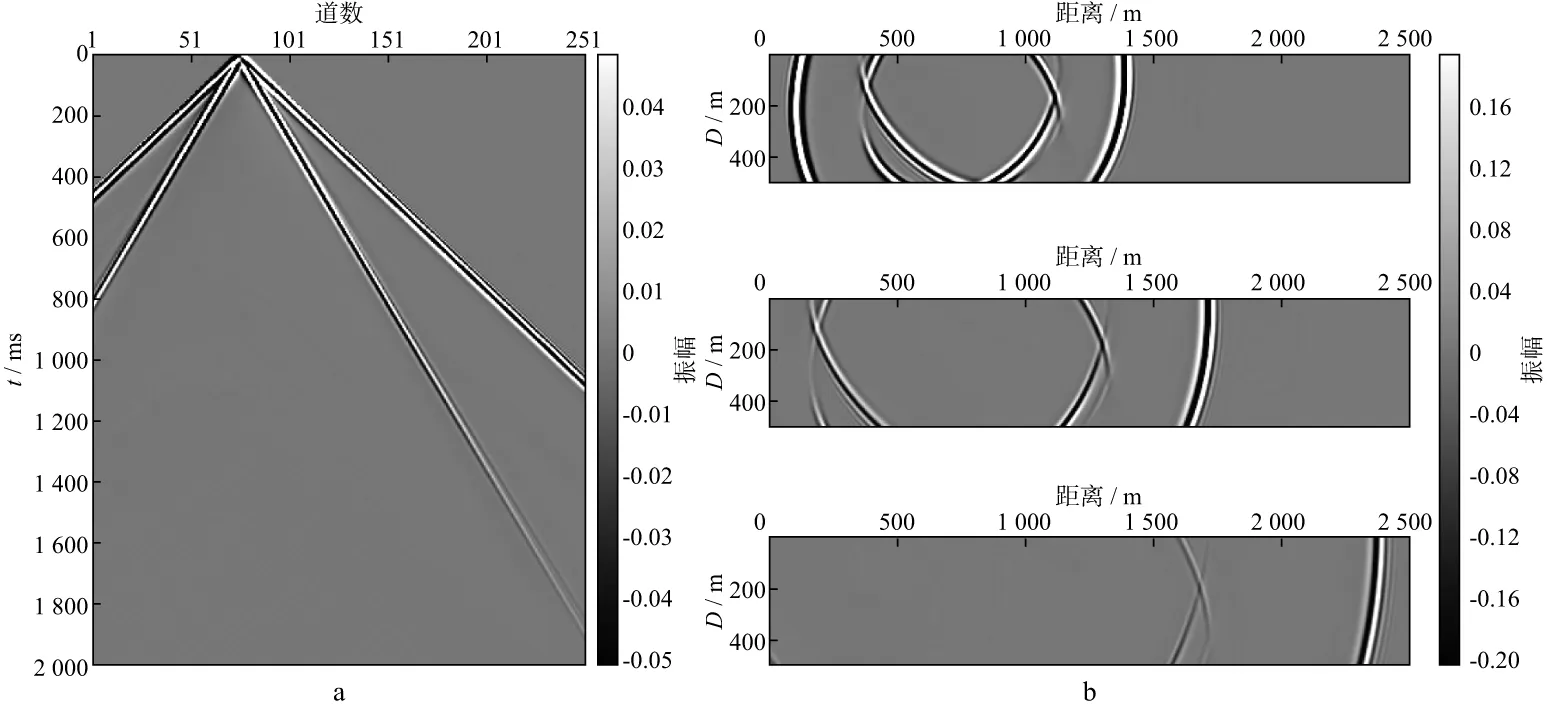
圖5 CPML-RML組合邊界條件的x分量地震記錄(a)與波場快照(b)

圖6對比了3種邊界條件第211道的地震記錄,圖6b為圖6a部分區域的放大結果。從圖6可以看出,SPML吸收邊界條件出現了較明顯的邊界反射,CPML吸收邊界條件則出現了弱邊界反射,而CPML-RML組合邊界條件未出現邊界反射。

不同邊界條件的計算效率如表2所示。表2中的計算效率是在Win10系統、i5CPU(2.7GHz)、4G內存以及VS2013+IVF2013編程環境下得出的。從表2中可以明顯地看到,粘彈TTI介質情形下,與SPML吸收邊界條件相比,CPML-RML組合邊界的計算效率高出18.2%,這是由于SPML吸收邊界條件需要將方程進行分裂而導致的,而CPML吸收邊界條件與CPML-RML組合邊界條件計算效率相當;同樣地,由于粘彈性TTI介質方程比彈性TTI介質方程多了記憶變量方程,因此,在相同的邊界條件下,彈性TTI介質方程的計算效率比粘彈性TTI介質方程高49.1%,但粘彈性TTI介質方程更能夠反映地下真實介質情況;另一方面,各向同性介質的計算效率比彈性TTI介質的計算效率高6.3%。

圖6 3種邊界條件第211道地震記錄對比a 顯示時間范圍為0～2.0s; b 顯示時間范圍為0.865～2.000s

因此,隨著介質復雜程度的提高,計算效率隨之降低,但更加接近地下真實介質的情況。此外,由于CPML吸收邊界條件不需要對方程進行分裂,因而其計算效率比SPML吸收邊界條件高,實現簡單,編程方便。由于CPML-RML組合邊界條件的吸收效果優于CPML吸收邊界條件,因此更加適用于粘彈性介質方程的數值模擬。

表2 不同邊界條件的計算效率

2.2 二維復雜Hess模型

為了說明CPML-RML組合邊界條件對復雜介質的適應性及正確性,采用二維Hess粘彈TTI介質模型進行測試。二維Hess模型大小為3000m×2500m,網格間距為5m×5m,時間步長為0.2ms,總時間采樣點數為12500,2.5s記錄長度,采用30Hz主頻的雷克子波,空間差分階數為20階,邊界層厚度為300m(對于組合邊界,CPML和RML邊界厚度各150m),震源位置為(2000m,10m),接收排列范圍為0～3000m,排列深度為0,接收點間距為10m,共301道接收。

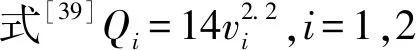
圖8給出了彈性TTI介質與粘彈TTI介質采用組合邊界條件在0.6s與0.8s時刻的波場快照。波場快照上未出現邊界反射,說明本文提出的組合邊界策略在復雜構造介質中的正確性及有效性;同時,也可以從波場快照中明顯地看見彈性TTI介質與粘彈TTI介質在能量及旅行時上的差異,表明粘彈介質存在振幅衰減及相位延遲。圖9給出了彈性TTI介質與粘彈性TTI介質采用組合邊界條件得到的地震記錄。由圖9也可以看出,彈性TTI介質與粘彈性TTI介質在能量及相位延遲上的差異,同時,在粘彈TTI介質地震記錄中,淺部能量強、深部能量弱,與實際采集得到的地震記錄特征相同,而彈性TTI介質未表現出該特征,說明采用粘彈TTI介質進行數值模擬更加符合實際地質情況,為研究地下波場特征提供了更多的理論依據。

圖7 二維Hess粘彈TTI介質(θ=0,φ=60°)模型參數a 縱波速度vP; b 橫波速度vS; c 縱波各向異性參數ε; d 橫波各向異性參數γ; e 變異系數δ; f 密度ρ; g 縱波品質因子Q1; h 橫波品質因子Q2

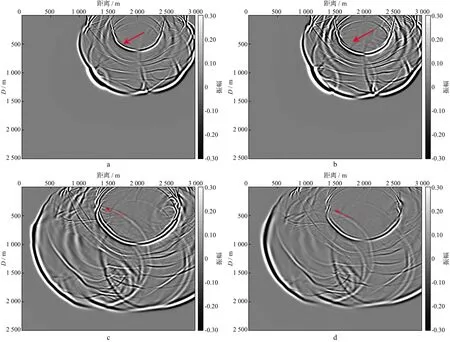
圖8 彈性TTI介質與粘彈性TTI介質采用組合邊界條件不同時刻波場快照a 彈性TTI介質0.6s時刻波場快照; b 粘彈TTI介質0.6s時刻波場快照; c 彈性TTI介質0.8s時刻波場快照; d 粘彈TTI介質0.8s時刻波場快照

圖9 彈性TTI介質(a)與粘彈性TTI介質(b)采用組合邊界條件得到的地震記錄

圖10為粘彈TTI介質分別采用SPML吸收邊界條件、CPML吸收邊界條件與CPML-RML組合邊界條件得到的地震記錄。對比圖10a、圖10b和圖10c 可以看出,采用SPML吸收邊界條件得到的地震記錄上出現了邊界反射,采用CPML吸收邊界條件得到的地震記錄上出現了低頻反射,而采用CPML-RML組合邊界條件未出現邊界反射,說明本文提出的組合邊界條件吸收效果好。

圖10 粘彈性TTI介質采用不同邊界條件得到的地震記錄a SPML吸收邊界條件; b CPML吸收邊界條件; c CPML-RML組合邊界條件

3 結束語

本文在前人對人工邊界條件研究的基礎上,提出了CPML吸收邊界條件與RML邊界條件相結合的策略,并將其應用于基于GSLS模型的粘彈TTI介質數值模擬中,同時給出了適用于粘彈TTI介質的CPML吸收邊界條件旋轉交錯網格有限差分算法,以提高數值模擬的穩定性及數值解的精確性。采用二維均勻介質模型和復雜Hess模型測試了本文組合邊界條件的適應性及正確性,驗證了其吸收效果,得到以下結論:

1) 與SPML吸收邊界條件、CPML吸收邊界條件相比,本文提出的組合邊界條件在不增加計算量的情況下具有更好的吸收效果,能有效減少人工邊界反射、提高數值模擬的精度,獲得更好的數值模擬結果,適合于粘彈TTI介質的數值模擬;

2) 與TTI介質相比,粘彈TTI介質中的地震波場表現出明顯的振幅衰減和相位延遲,地震記錄中淺層能量強、深層能量弱,較好地表現出了地下真實介質的粘滯性特征。說明本文組合邊界條件適用于復雜地下介質。