一種基于Multi-Egocentric視頻運動軌跡重建的多目標跟蹤算法

歐偉奇，尹輝，許宏麗，劉志浩

（1. 北京交通大學 計算機與信息技術學院，北京 100044; 2. 北京交通大學 交通數據分析與挖掘北京市重點實驗室，北京 100044）

目標跟蹤是計算機視覺重要研究領域之一，在智能交通、運動分析、行為識別、人機交互[1]等方面具有廣泛應用。隨著可穿戴式相機的普及，基于Egocentric視頻的目標跟蹤引起研究人員的極大興趣。由于單視角視野有限，當相機劇烈晃動時易造成目標丟失以至于跟蹤軌跡的不連續性問題，無法進行全方位的跟蹤。Multi-Egocentric視頻是由多個處于同一場景中的穿戴式或手持式相機所拍攝的不同視角、不同運動軌跡的視頻。多視角跟蹤由于視野范圍更大，視角豐富，能夠根據多視角信息有效跟蹤目標。相對多固定視角視頻的跟蹤任務，Multi-Egocentric視角隨拍攝者移動，一方面帶有Egocentric視頻背景變化劇烈、目標尺度差異明顯和視角時變性強的特點，另一方面由于繼承了拍攝者的關注興趣，能以更好的視角拍攝所關注的目標，同時多樣化的視角為解決遮擋、漂移等問題提供了更為豐富的線索。

目前大多數跟蹤算法致力于解決單個Egocentric視角或多個固定視角中存在的目標遮擋、跟蹤漂移等問題[2-5]。為了進行魯棒的目標跟蹤，Xu等[4]基于目標表面模型和運動模型，提出層次軌跡關聯模型構建有向無環圖解決固定多視角下軌跡片段關聯問題，將其應用于Multi-Egocentric視頻魯棒性較差，無法解決目標不連續性問題。Fleuret等[6]將顏色、紋理和運動信息3個特征相結合建立目標模型，并通過目標之間的相對位置對目標進行定位，能夠有效解決多固定視角下目標遮擋問題，但是將其應用于Multi-Egocentric視頻跟蹤任務中，背景變化劇烈情況會對跟蹤結果造成很大影響，常出現軌跡誤匹配問題。另外，X.Mei等[7]提出的稀疏表示算法采用稀疏線性表示的方法使跟蹤器可以應對光照變化、遮擋等問題。在線多示例學習算法[8]使用圖像塊的集合表示目標，使得跟蹤器在目標經歷光照變化和遮擋時可以有效地跟蹤目標。Yuxia Wang等[9]采用粒子濾波方法，基于貝葉斯濾波理論，解決狀態估計問題，再根據所有粒子的權重，利用蒙特卡洛序列方法確定狀態的后驗概率，對跟蹤過程中噪聲具有一定的魯棒性。Bae等[10]以及Dicle等[11]跟據軌跡片段的置信度進行軌跡關聯實現多目標跟蹤，但由于目標軌跡不連續，容易造成短時間的目標誤匹配問題。Xiang等[12]通過構造馬爾可夫決策過程求取最優策略的方法來預測目標下一刻狀態。上述算法一定程度上能夠解決運動視角下目標的魯棒性跟蹤問題，但對于視角時變性強的Multi-egocentric視頻，容易因目標運動不連續性造成跟蹤失敗。近年來深度學習方法在目標跟蹤領域也有廣泛應用，其中MDNet算法[13]采用共享層和特定層相結合的深度模型進行目標跟蹤，該方法具有很好的魯棒性和適應性，但對多目標跟蹤具有局限性。

針對Multi-egocentric視頻的特點，本文從目標空間幾何關系約束的角度出發，并結合卡爾曼濾波算法，提出一種基于運動軌跡重建的多目標跟蹤算法。與以上算法相比，本文算法通過軌跡重建可以有效解決Multi-egocentric視頻中運動目標軌跡不連續的問題。

1 基于運動軌跡重建的多目標跟蹤

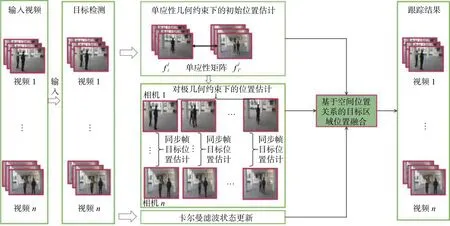
圖1 基于運動軌跡重建的多目標跟蹤算法流程Fig.1 Flow chart of multi-target tracking algorithm based on trajectory reconstruction

本文針對Multi-egocentric視頻的特點，提出一種基于運動軌跡重建的多目標跟蹤算法，算法流程如圖1所示。該算法利用多視角之間目標位置和運動軌跡的幾何約束關系降低了目標定位誤差、目標跟蹤漂移以及軌跡不連續等對多目標跟蹤造成的影響，并在Multi-Egocentric視頻數據集和多固定視角數據集上驗證了本文算法的有效性。與單視角目標跟蹤算法不同，多視角目標跟蹤可以利用多視角之間目標位置的關聯關系優化目標定位；本文提出基于運動軌跡重建的Multi-Egocentric視頻多目標跟蹤算法，首先在目標檢測基礎上，通過求解不同視角間單應性約束解決同一時刻目標的遮擋和丟失問題，然后基于多視角軌跡立體重建算法進行目標定位估計，最后結合卡爾曼濾波的狀態更新實現基于空間位置關系的目標區域位置融合，得到最佳的目標跟蹤結果。

1.1 多視角輔助下的目標初始位置估計

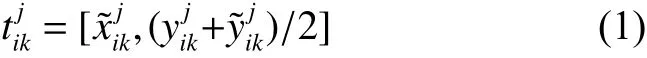
由于Egocentric視頻視角時變性的特點，移動視角因劇烈晃動或平移等因素造成單個視角中目標消失等運動軌跡的不連續性問題。如圖2所示，箭頭指示兩個視角下的相同目標所在位置。從Camerai視角方向來看，兩個目標在同一個方向造成目標遮擋，而Camerai'的視角中各目標無遮擋問題。如圖3所示，左右兩視角都向兩邊移動時，造成單個視角只檢測到部分目標，右側擴充區域是對單個視角的視野范圍的擴充，用于顯示目標之間的相對位置關系。以上兩種情況都會因目標丟失導致某些視角跟蹤失敗。

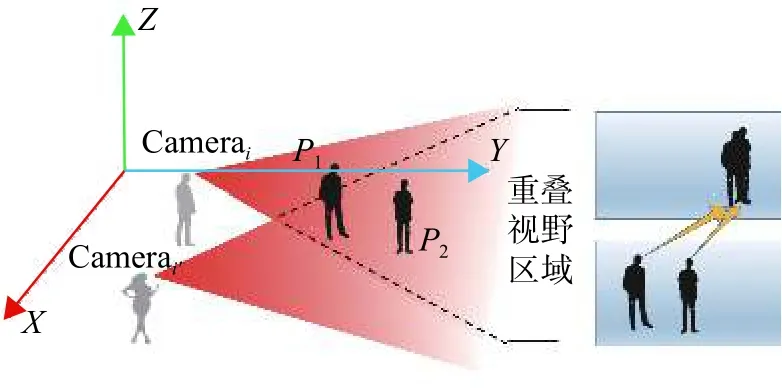
圖2 多視角中目標之間相互遮擋示意圖Fig.2 Multi-view of the occlusion between targets

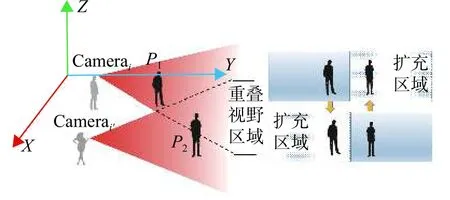
圖3 多視角移動造成目標丟失示意圖Fig.3 Multi-view movement causes the target to lose the sketch map

針對這種問題，本文基于具有重疊視野區域的視角之間存在平面上的單應性約束關系[14]，利用多個視角之間目標的相對位置，根據Camerai第 j幀中的目標軌跡點來估計Camerai'第 j幀的目標所在位置。算法具體描述和實現如算法1所示。

算法1多視角單應性約束下的目標位置估計

輸入1) Camerai第 j幀、Camerai'第 j幀、中被遮擋目標k在中的軌跡點坐標；

4) 利用匹配點構建方程(2)，并利用RANSAC[15]算法剔除誤匹配點求解單應性矩陣；

式中： H 為3×3的單應性矩陣。

輸出的目標所在位置

通過不同視角同一時刻目標之間存在的單應性約束關系可以對遮擋和丟失目標進行重新定位，從而解決單個視角中目標的遮擋和丟失問題。同時由于特征點的檢測和匹配誤差使得單應性約束只能粗定位遮擋和丟失的目標，因此本文通過多視角軌跡重建進一步優化目標位置估計。

1.2 多視角軌跡重建位置估計

多視角軌跡重建位置估計是根據不同視角同一時刻幀目標的像素坐標對應位置關系做空間約束進一步對目標進行定位。根據不同視角同步幀之間重疊視野區域特征點的對應關系采用立體視覺三維重建算法實現同步幀目標位置估計。立體視覺三維算法示意圖如圖4所示，相機i采用張正友標定法[16]獲得Camerai內參矩陣 Ki和Camerai'內參矩陣 Ki′，然后分別提取和之間重疊區域的匹配點集合和，由單應性約束得：

利用PnP[17]和RANSAC算法求出基礎矩陣和本質矩陣；當中目標k在Camera中沒i'有對應位置，把目標軌跡點代入式(3)可以求解目標在中的擴展匹配坐標位置，并把和分別加入和。對作SVD分解，可得 Camera相對于Camera的旋轉矩陣和平移向量i'i。然后計算得到目標軌跡點的三維空間坐標位置集合={|k=1,2,···,m}。

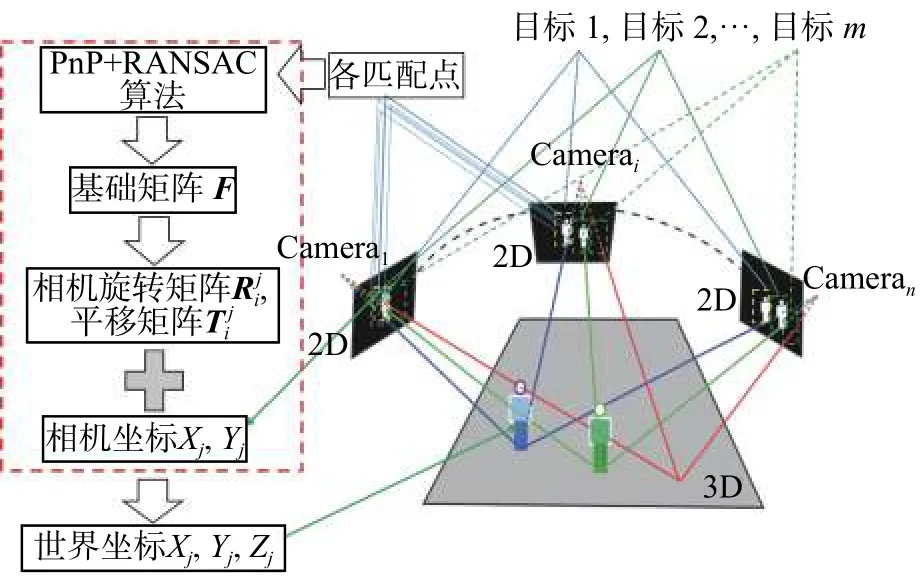
圖4 同步幀目標位置估計算法圖Fig.4 Sketch map of synchronous frame target location estimation algorithm

1.3 基于軌跡重建的多目標跟蹤

設置目標的運動狀態參數為某一幀目標的位置和速度。定義卡爾曼濾波[18]第k個目標在j時刻狀態是一個四維向量 rk(j)=)，分別表示目標在x軸和y軸上的位置和速度，設單位時間T內假設目標是勻速運動、初始位置為初始速度設為0、rk(0)=(s 0,yk,pos,0)T；其中下一步預測方程為

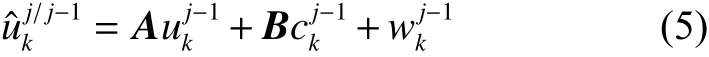
由系統方程和觀測狀態定義矩陣 B為

卡爾曼濾波狀態更新方程為

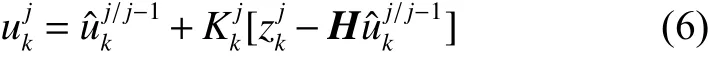
1.4 基于空間位置關系的目標區域位置融合

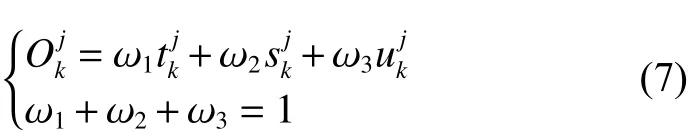
式中 ω1、ω2和ω3分別表示和的權重。

2 實驗結果與分析

本文提出的基于Multi-Egocentric視頻運動軌跡重建的多目標跟蹤算法是針對Multi-Egocentric視頻的，目前尚無針對此任務的公開評價數據集，為了驗證算法的有效性，設計并拍攝了針對多目標跟蹤任務的Multi-Egocentric視頻數據集BJMOT。由于數據集采集規模所限，該視頻數據集包含兩個視角的視頻，由兩個拍攝者佩戴相同規格的運動相機拍攝，場景中有兩個以上的自由運動目標，各視頻經同步后，每個視頻時長為45 s，幀率為每秒25幀，并從每個視頻各提取220幀進行了人工標注作為ground-truth。同時為了驗證本文算法的適應性，還在固定多視角的數據集EPLF-campus4進行了跟蹤實驗，表1為兩個數據集的相關信息。

表1 實驗采用的數據集Table1 Experimental data sets information

本文采用的目標檢測方法為ACF算法[19]，并將算法與MDP算法[12]和CMOT算法[10]進行了對比說明。實驗評價指標采用中心位置誤差和重疊率兩種度量方式。中心位置誤差是跟蹤結果和實際情況中心點間的歐式距離，重疊率是PASCAL中目標檢測的評分標準[20]，即對于給定的跟蹤目標框為 rt和 ground-truth為 rg，定義中心位置誤差為

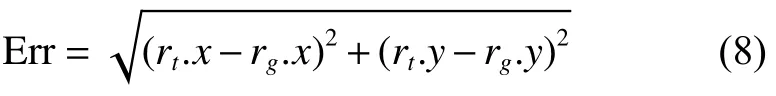
式中： rt.x 和 rt.y 分 別表示 rt的中心橫坐標和縱坐標， rg.x 和 rg.y 分 別表示 rg的中心橫坐標和縱坐標，定義目標框的重疊率為

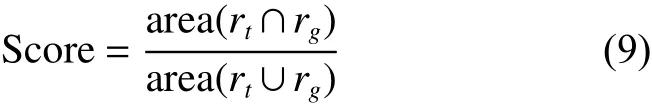
2.1 在BJMOT數據集上的實驗結果

本文算法在BJMOT數據集上的平均中心誤差如圖5所示，表2為平均重疊率和平均中心誤差的統計結果，對于部分目標丟失的情況不在計算中心誤差范圍之內。實驗過程中，對 ω1、ω2和ω3分 別 取 值 為 ω1=0.64,ω2=0.23,ω3=0.13。 相 比缺少單應性約束條件的實驗結果，結合單應性約束的目標初始位置估計和多視角軌跡重建的方法下，本文算法實驗結果的平均重疊率在第一個視角和第二個視角分別提高了13%和9%，能夠有效降低遮擋或部分丟失等因素造成的不連續因素對跟蹤的影響。

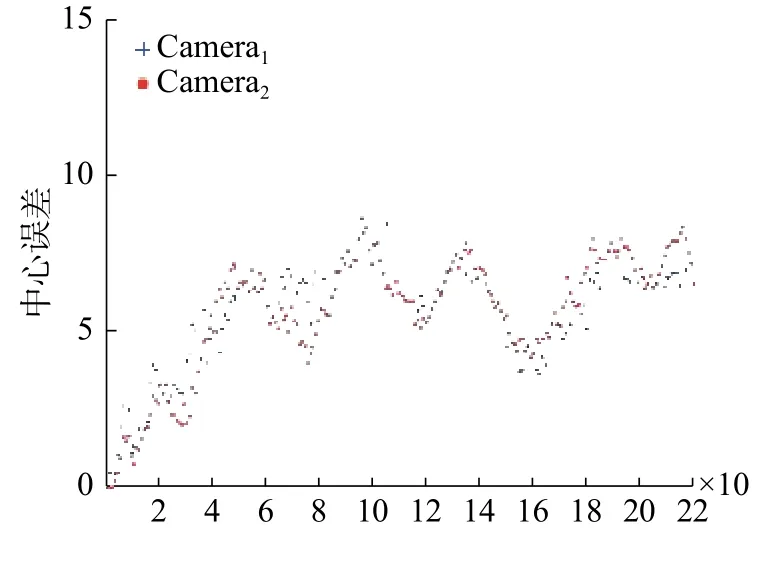
圖5 本文算法在BJMOT數據集的中心誤差曲線Fig.5 The central error curve of the algorithm in BJMOT dataset

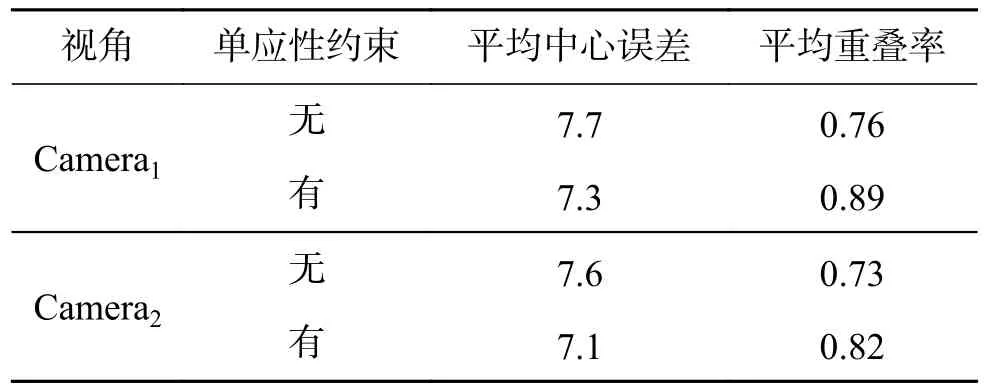
表2 本文算法在BJMOT上的平均中心誤差和平均重疊率Table2 The mean center error and the average overlap rate of the proposed algorithm over BJMOT

部分典型幀在Camera1和Camera2上的實驗結果分別如圖6～7所示，圖6～7中給出正常情況、部分遮擋情況、完全遮擋情況、部分消失和完全消失情況等5種典型情況下的目標跟蹤實驗結果。其中第1行表示目標檢測結果或單應性約束目標位置估計結果，行中實線框表示目標檢測結果，虛線框表示單應性約束計算結果；第2行中虛線框為多視角軌跡重建估計結果；第3行中虛線框為卡爾曼濾波當前時刻的最優估計值；第四行表示最終結果。第5列中由于目標缺失，在跟蹤過程中通過運動一致性可以有效定位目標所在位置，算法計算出的結果在擴展視野區域；并且從圖6中第2行第3列也可以看出，通過軌跡重建得到的目標位置誤差較大，實驗結果容易受到目標檢測算法和單應性計算結果的影響；當目標檢測誤差較大時，該部分所產生的誤差也較大，而通過融合對這類誤差進行了較好的修正。

圖6 本文算法在BJMOT數據集第1個視角視頻中的分步實驗結果Fig.6 The experimental results of ours algorithm in the first video sequences of the BJMOT datasets

圖7 本文算法在BJMOT數據集第2個視角視頻中的分步實驗結果Fig.7 The experimental results of ours algorithm in the in the second video sequences of BJMOT datasets

2.2 在EPLF-campus4數據集上的實驗結果

本文算法與MDP算法、CMOT算法在EPLF-campus4數據集上的平均重疊率結果對比如表3所示。表4為3個跟蹤器在EPLF-campus4數據集上的平均中心位置誤差。從表3中看出，相比其他兩種算法，本文算法在Camera1中的重疊率更高，而在Camera2中的重疊率較低于CMOT算法，其原因是在CMOT算法中目標跟蹤框不會隨著目標大小進行變化，在目標較遠時，檢測框與目標真實范圍重合率較大。從表4可以看出本文的算法的平均中心誤差較小。因此從整體來看本文算法在該數據集上優于其他兩種算法。圖8～9是3種算法在EPLF-campus4數據集中兩個視角的中心誤差變化趨勢。

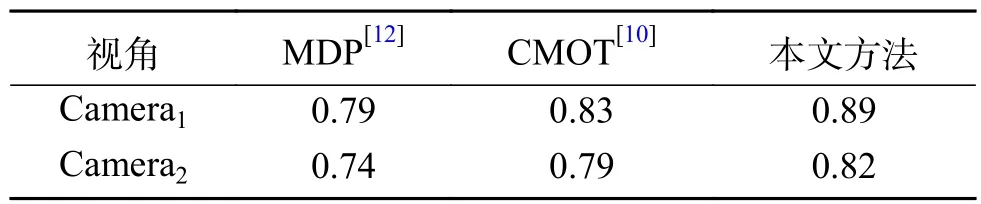
表3 3個跟蹤算法在EPLF-campus4上的平均重疊率Table3 The average overlap rate of3tracking algorithms on EPLF-campus4

表4 3個跟蹤算法在EPLF-campus4上的平均中心誤差Table4 Average center error of3tracking algorithms on EPLF-campus4

圖8 3種算法在Camera1視頻中的中心誤差曲線Fig.8 The center error of three tracking algorithms on camera1

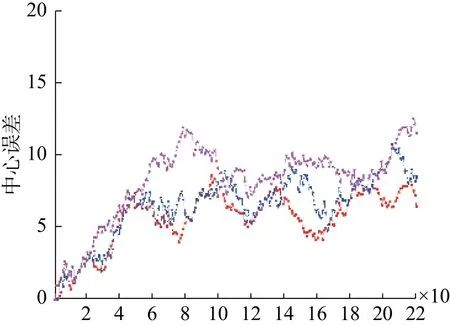
圖9 3種算法在Camera2視頻中的中心誤差曲線Fig.9 The center error of three tracking algorithms on camera2

在EPLF-campus4數據集上Camera1和Camera2的典型幀跟蹤結果分別如圖10～11所示。同樣選取五種典型情況下的目標跟蹤實驗結果進行分析。其中虛線框表示單應性約束計算結果。第五列中由于目標缺失，算法結果在擴展視野區域，橢圓區域為不同跟蹤算法產生的差異性結果對比。從橢圓區域可以看出，本文算法能夠根據視角之間的位置信息更好定位到目標，MDP算法在遮擋情況下出現目標丟失，CMOT雖然能跟蹤到目標，但是其偏離目標中心位置，誤差較大。

圖10 3種算法在EPLF-campus4數據集第一個視角視頻中的跟蹤對比結果Fig.10 Tracking results of three algorithms in the first video of EPLF-campus4 datasets

圖11 3種算法在EPLF-campus4數據集第二個視角視頻中的跟蹤對比結果Fig.11 Tracking results of three algorithms in the second video of EPLF-campus4 datasets

3 結束語

本文針對Multi-Egocentric視頻中的目標遮擋和丟失問題，提出了基于多視角運動軌跡重建的多目標跟蹤算法，利用多視角之間單應性約束和空間位置約束關系，結合卡爾曼濾波解決目標在不連續情況下的跟蹤問題。與相關算法的對比實驗結果表明，本文利用多視角的信息更加有效地解決了多目標跟蹤不連續性問題。本文在單應性估計和軌跡重建方面仍然有改進空間，可以通過提高特征點匹配的準確性進一步提高本文算法的準確性。