一類分數階神經網絡的自適應H∞同步

袁曉琳，莫立坡

（北京工商大學 理學院，北京 100048）

由于分數階算子具有許多良好的性質，如記憶性和遺傳性，近年來這一領域吸引了眾多學者的研究。如：Zhang等[1]為分數階系統提出了許多簡化的LMI穩定性條件，Li等[2]研究了分數階非線性動態系統的Mittag-Leffler穩定性等。

人工神經網絡的概念由McCulloch等首次提出[3]。隨后Hopfield提出了一個新的名為Hopfield神經網絡的循環神經網絡[4]，這為解決優化問題和數值計算問題做了很大的貢獻。目前，神經網絡被廣泛應用于許多的領域，例如，模型預測[5]、自動化控制[6]以及優化[7]。但大部分結果都假設系統的動態模型是整數階的。然而，在很多實際應用中，分數階微分方程能夠更好的描述實際系統。目前，有許多關于分數階神經網絡同步問題的研究結果，如自適應同步[8]、全局同步[9-10]、有限時間同步[11-12]、 α 同步[13]等。此外，當系統中存在未知參數時，文獻[14]研究了此類分數階神經網絡的自適應同步問題。事實上，除系統參數外，系統的輸入也可能是未知的，并且系統不可避免地受外部干擾。然而，據我們所知，目前很少有關于這方面的研究結果。

受文獻[15-16]的啟發，本文用 H∞控制的方法來研究了一類分數階神經網絡的 H∞同步問題。提出了一個使閉環系統實現自適應同步和自適應H∞同步的自適應控制協議。并且通過利用魯棒控制方法和Gronwall-Bellman不等式完成了閉環系統的收斂性分析及 H∞性能分析。與文獻[17]相比，它所考慮的是無外界干擾的整數階神經網絡模型，而我們在這篇論文中考慮了分數階的動態模型，同時考慮了未知外部干擾的影響。與文獻[14]相比較，它模型中的外部輸入是已知的，而在此篇論文中考慮了未知的外部輸入。眾所周知，H∞性 能主要是用于刻畫系統的輸入輸出間關系的一種性能指標，文獻[14]并沒有研究系統的H∞性能，在本文中我們做了相應的研究。

1 分數階算子的基礎理論知識

本部分主要介紹分數階算子的定義和相關引理，這對于我們以后的分析是非常重要的。

定義1[18]函數 f的Riemann-Liouville型 α階分數階積分定義為

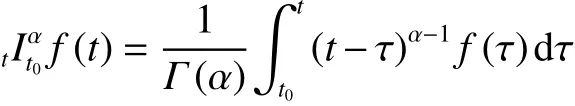
式中： t ≥ t0;0 ＜ α ＜ 1;Γ(·)表示Gamma函數。

定義2[18]函數 f ∈Cn([t0,+∞),R)的Caputo型α階分數階微分定義為

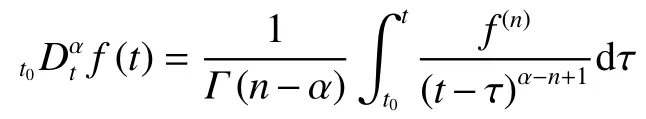
式中： t ≥t0;n 是 一個正整數使得n-1＜α＜n.特別地，當 0 ＜α＜1時，

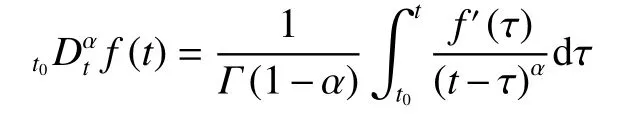
引理1[19]設函數 g (t)在 t ∈[t0,b]上是連續可微的，則對任意的常數及 t ∈[t0,b]有

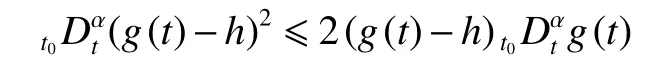
其中 0 ＜α＜1。

引理2[20]令 n =[α]+1， 當 α ?N 時 ，或令n=α當 α ∈N 時 。如果 y (t)∈Cn[t0,b]，則

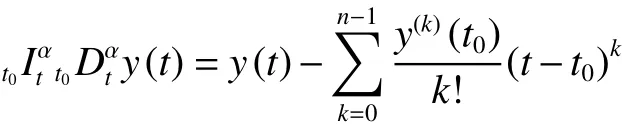
特 別 地 ， 當 0 ＜α＜1 及 y (t)∈C1[t0,b] 時 ， 有)=y(t)-y(t0)。

引理3[14]假設 x (t),y(t)∈C1[t0,b]， 如果對?t∈[t0,b]有 x (t)≤y(t)，則t0x(t)≤t0y(t)。

引理4[21](Gronwall-Bellman 不等式)若存在x(t)滿 足 x (t)≤a(τ)x(τ)dτ+b(t)， 其中 a (t)和 b (t)是兩個已知的實函數，則

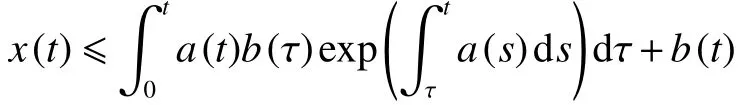
如果 b (t)是可微的，從而

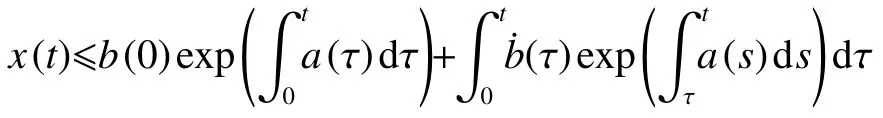
如果 b (t)是一個常數，從而

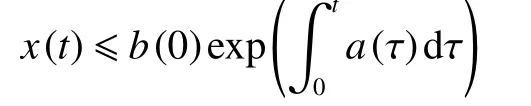
引理5[22-23]Riemann-Liouville型分數階非線性微分方程 Dαxi(t)=fi(x(t)),i=1,2,···,N，可以被表示成

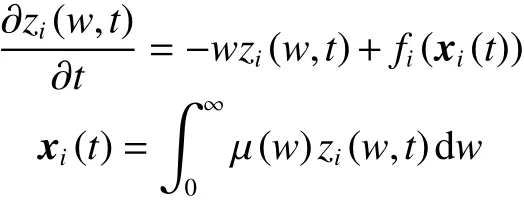
2 研究問題的系統模型描述

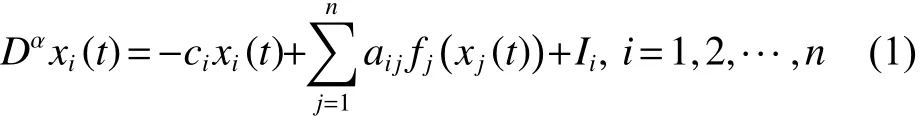
考慮如下分數階神經網絡作為驅動系統式中： 0 ＜ α ＜ 1;i=1,2,···,n,n表示神經元的個數；xi(t)∈R 是 第i個 神經元在t時 刻的狀態；ci是一個正的常數，表示第i個神經元在無任何連接情況下恢復到靜息狀態的速率； aij表 示第 j個神 經 元與第i個神經元之間的連接權重，并且滿足 aij≤ μ,其中μ是一個正常數；Ii表示是外部輸入，它是不可以被獲得的； fj(·)是 第 j個神經元的激勵函數，它滿足全局的李普希茲條件，即存在 Lj＞0使得

式中： u ,v ∈ R;j=1,2,···,n。

考慮如下響應系統：

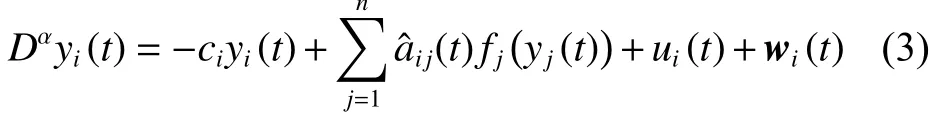
式中： yi(t)∈R是響應狀態； aij(t)表示 aij(t)的參數估計值； ui(t)是 控制輸入， wi(t)是未知的外部干擾，它們屬于：

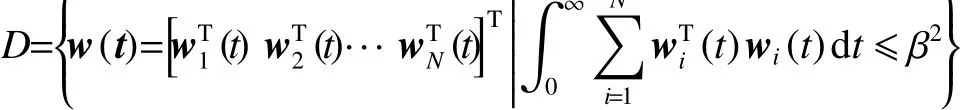
其中 β ＞0是一個正常數。

定義3[18]稱驅動系統(式(1))與響應系統(式(3))是全局漸近同步的，如果存在控制器ui(t),i=1,2,···,n使得

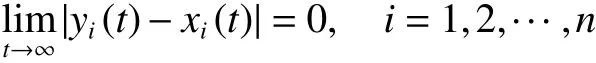
3 一致性收斂分析

3.1 自適應同步

考慮閉環系統的零輸入響應，即研究當外部干擾不存在時系統式(1)和式(3)的同步問題。為此，設計如下自適應控制律：

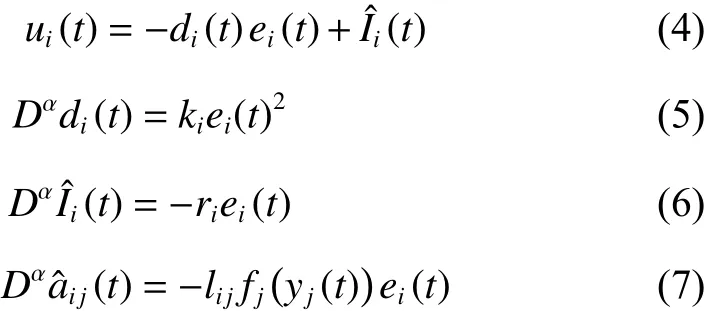
式中： ei(t)=yi(t)-xi(t),i=1,2,···,n定義為狀態誤差 ； Ii(t)∈R定 義 為 未 知 外 部 輸 入 的 估 計 值 ；di(t)∈ R 是 時變的控制強度； ki、ri和 lij是正常數，它們的取值待定。

利用自適應控制律式(4)～(7)，動態誤差閉環系統可以寫成如下形式：

注1 我們通常所說的控制律(控制協議)是指一系列信息傳輸規則，當驅動系統采取該控制律時，可以與響應系統實現同步。與傳統的控制律形成對比，本文設計了新的自適應控制律(4)～(7)，且控制律中 di(t)、 Ii(t)、 aij(t)的動態方程是分數階的，因而更具有一般性。除此之外，利用該控制律還可以對未知參數 aij(t)進行估計。

定理1對任給的正常數 ki,ri,lij,i,j=1,2···,n。如果外部干擾不存在，即 wi(t)=0,i=1,2,···,n,那么利用自適應控制律(4)和參數估計器(5)～(7)，驅動系統(1)和響應系統(3)可以實現全局漸進同步。

證明定義如下類似李雅普諾夫函數：

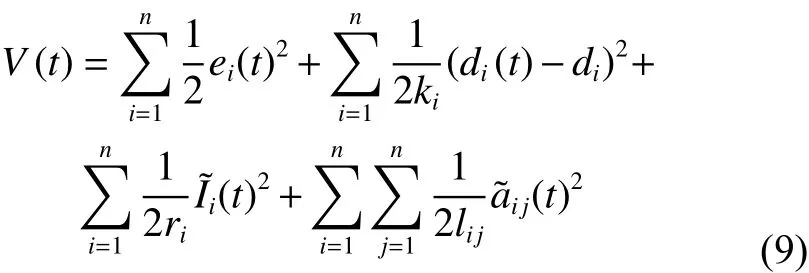
注意到

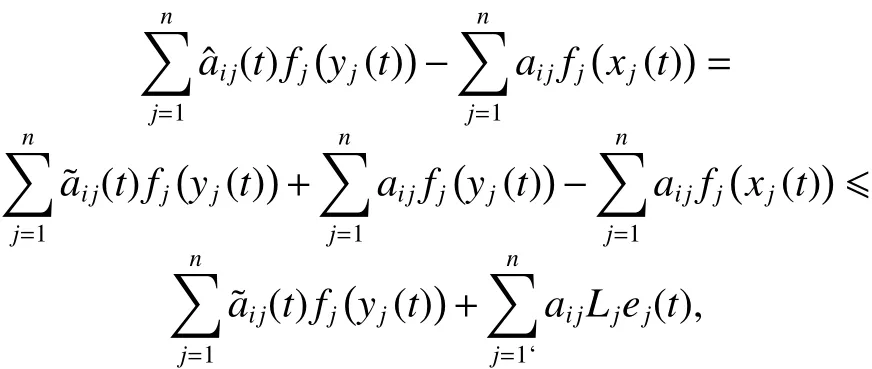
其中 μ =sup(aij),εi＞ 0是一個正常數。

利用引理1，計算系統(9)的 V (t)的 α階Caputo型導數，有

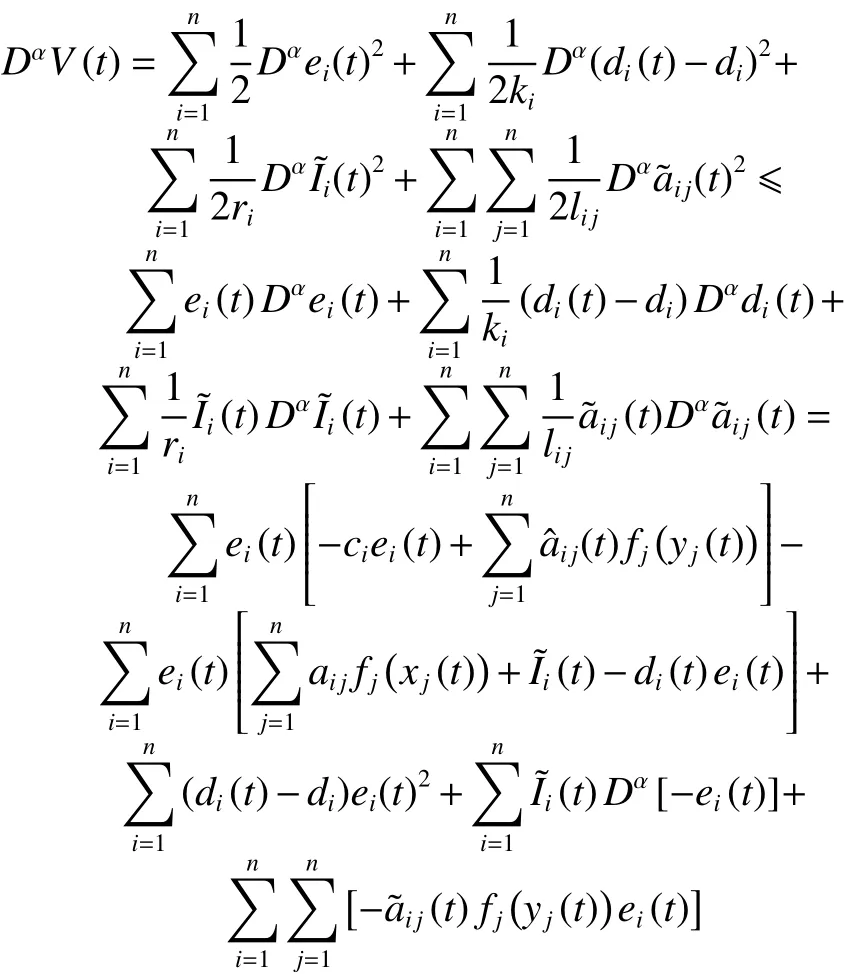
從而

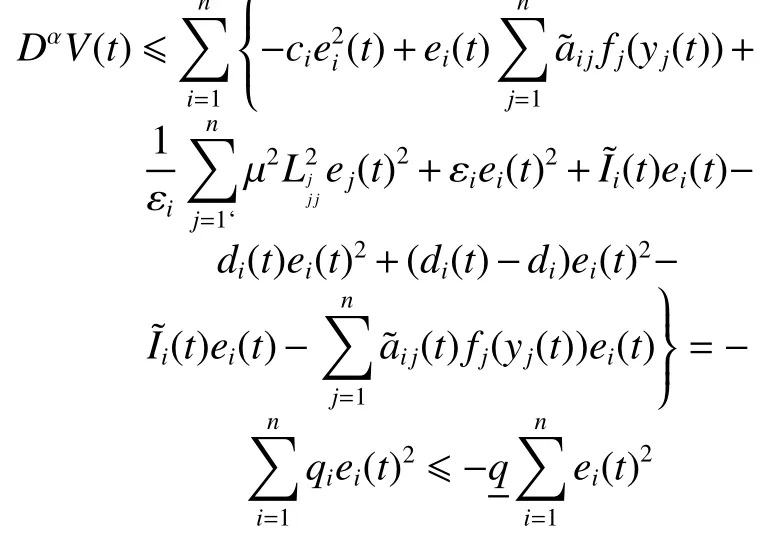
事實上，我們可以通過取足夠大的 di來 保證qi＞0,

由引理2和3可得

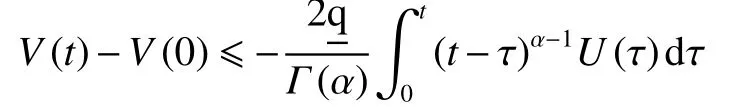
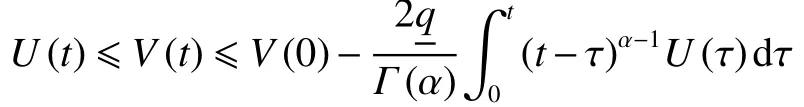
利用引理4，可以得到

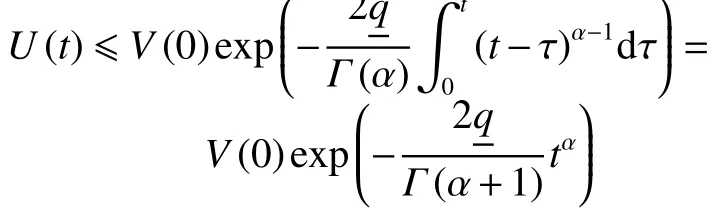
綜上，利用控制律(4)～(7)，響應系統與驅動系統可以實現自適應同步。

注2在定理1中，我們只能保證驅動系統和響應系統可以實現同步。為了對所有的未知參數進行辨識，需要對激勵函數 fj(·)添加額外的條件。基于誤差系統(8)，當兩個系統實現同步時，誤差系統可以被重寫為如下形式：

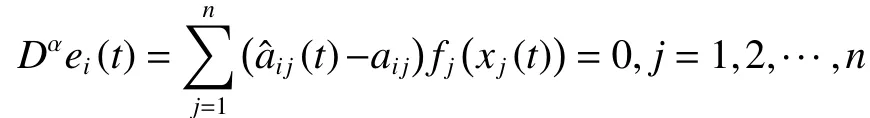
根據函數線性無關的條件，當 fj(xj(t))線性無關時可以對未知參數進行辨識。

注3 與其他相關文獻中設計的控制協議相比，如文獻[14]，我們所考慮的是帶有未知參數和未知外部輸入的系統。因此，文獻[14]中所考慮的模型是本文的特例。

3.2 自適應 H ∞同步

利用 H∞性能指標來研究外部干擾對系統同步的影響。

定理 2考慮驅動系統(式(1))和響應系統(式(3))。利用控制律式(4)和估計器即式(5)～(7)，則對于給定 γ ＞0 ， 誤差系統(8)可以滿足 H∞性能，即在零初始條件下可以滿足 ‖Tzw(s)‖∞＜ γ。

證明由于在零初始條件下，Caputo型導數與Riemann-Liouville型導數等價，利用引理5，誤差系統(8)和估計(5)～(7)可以用以下分布表示：

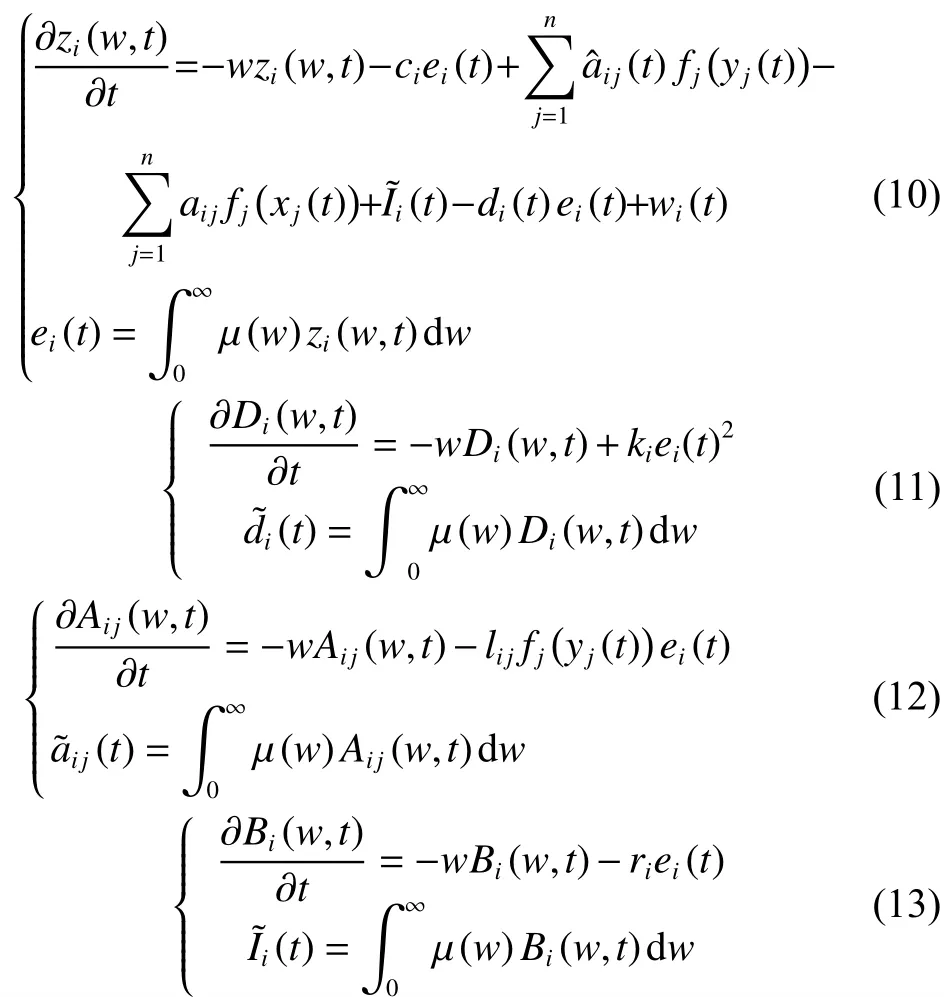
式中： i ,j=1,2,···,n;d?i(t)=di(t)-di;zi,Aij,Bi,Di,均是無限維的分布式狀態變量； μ (w)在引理5中被定義。定義如下類似李雅普諾夫函數：

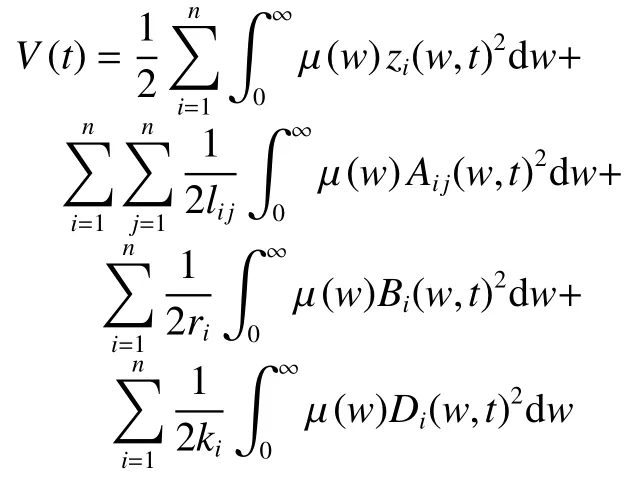
從而 V (t)的導函數為

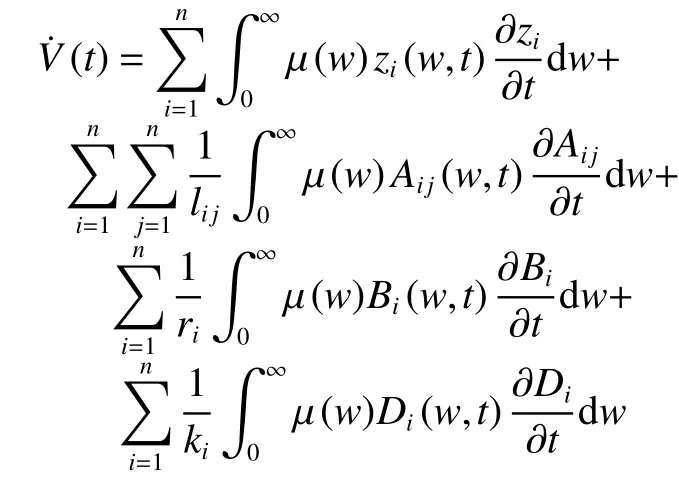
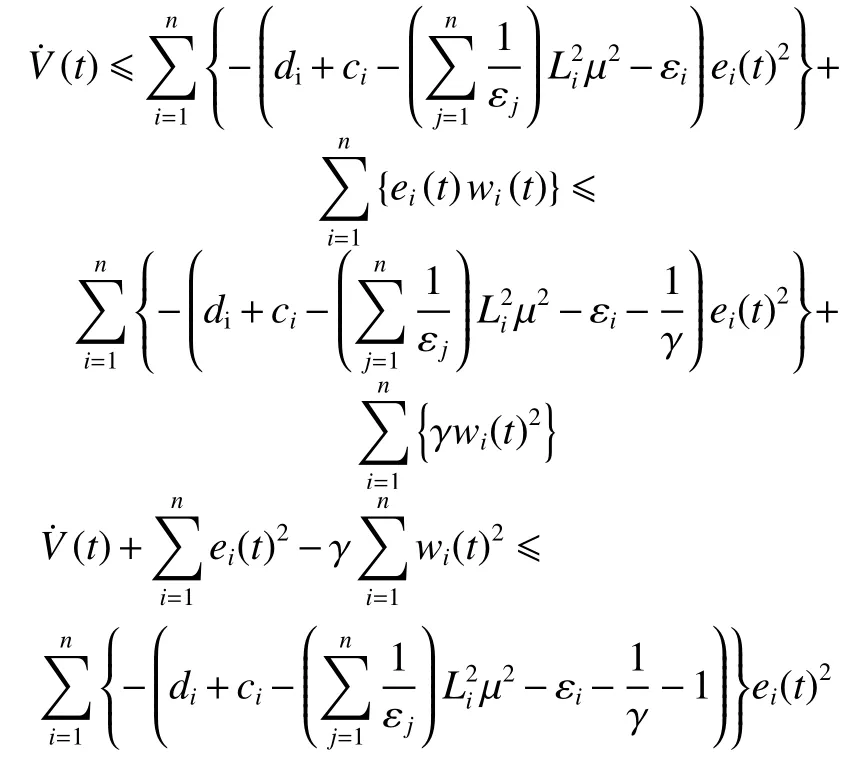
可以通過取足夠大的 di值使得

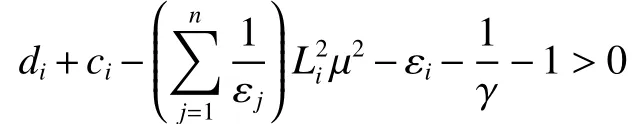
注4目前，關于 H∞控 制問題的研究主要集中在整數階系統，比如文獻[15-16]。本文通過利用分數階微分方程的分布式表達形式將這些結果推廣到了不確定分數階神經網絡系統，提出了一個可以使閉環系統實現 H∞同步的自適應協議。

4 仿真實驗

通過給出的仿真實例來驗證我們所提出的控制器在實現自適應同步和 H∞同步方面是有效的。此外，我們討論了相關的參數辨識問題。

例：對于驅動系統(式(1))，響應系統(式(3))以及控制協議即式(4)～(7),令

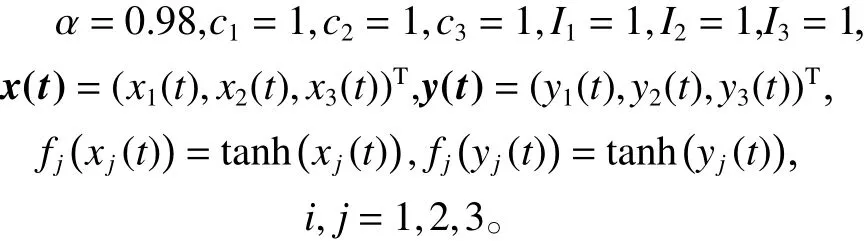
以及

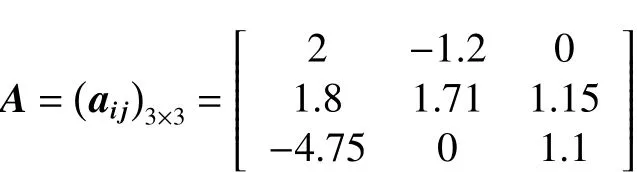
選取初始條件為

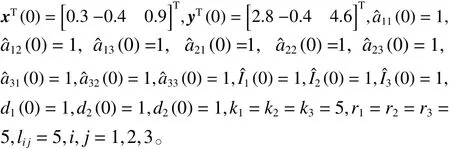
圖1為驅動系統(1)和未加控制器的響應系統(3)的狀態軌跡圖，顯然兩個系統并沒有實現同步。

圖1 驅動系統(1)與未加控制器的響應系統(3)狀態圖Fig.1 States of drive system (1) and response system (3)without controller

圖2 為驅動系統(1)和加了控制律(4)～(7)的響應系統(3)的狀態軌跡圖，該圖顯示利用控制律(4)～(7)這兩個系統實現了同步。

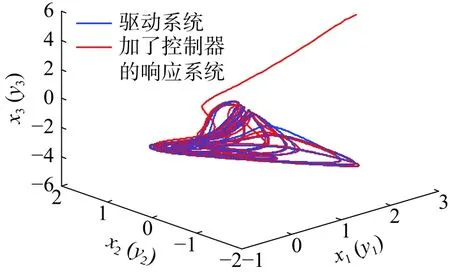
圖2 驅動系統(1)與加控制律響應系統(3)狀態圖Fig.2 States of drive system (1) and response system (3)with controller

圖3 為控制強度，當時間趨于無窮時它們都收斂到一個確定的常數。從圖4～6可以看出響應系統中(3)中所有的未知參數可以很好地辨識出來，辨識值為

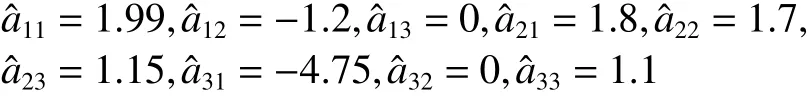
與權重矩陣 A 中的初始值相一致。這表明所提出的控制器是有效的并且可以精確地辨識所有的未知參數。

若將初始值改變為

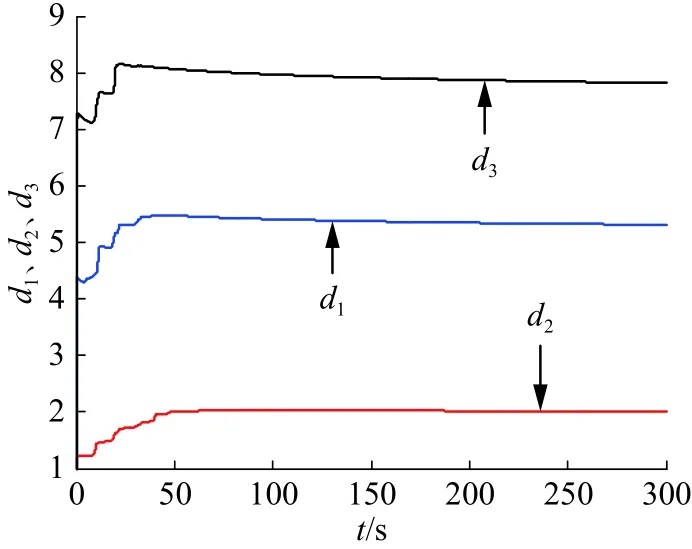
圖3 d 1、d2、d3 隨 時間t的變化圖Fig.3 d 1,d2,d3varies with time

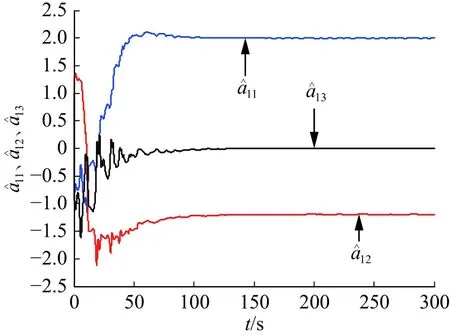
圖4 、、的辨識Fig.4 Identification of3

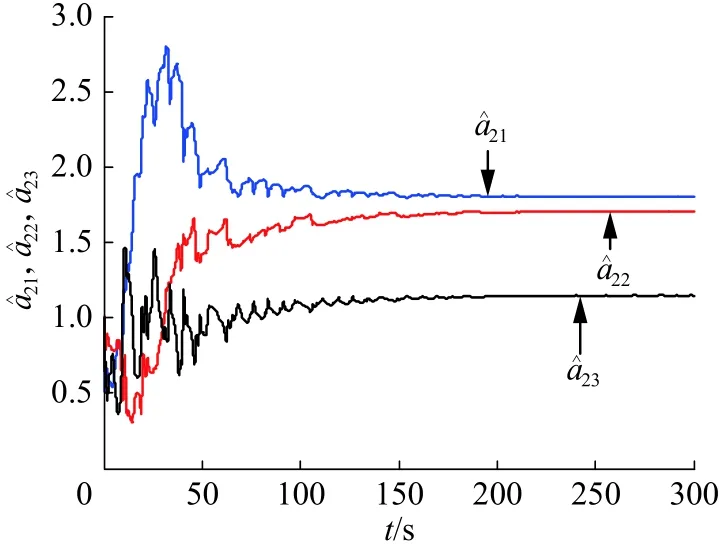
圖5 、、的辨識Fig.5 Identification of3

圖6 、、的辨識Fig.6 Identification of3

并且添加條件：

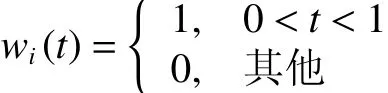
式中i = 1，2，3。通過圖7可以讀出γ=0.466 3。

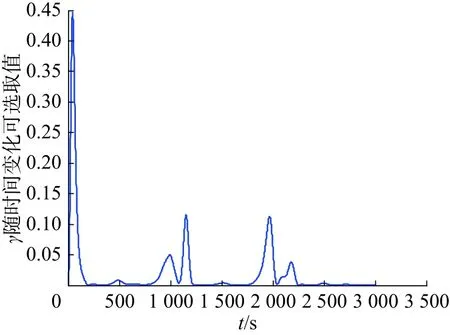
圖7 γ隨時間變化可選取值圖Fig.7 The value of γ varies with time

圖8 顯示當 t →∞時，有

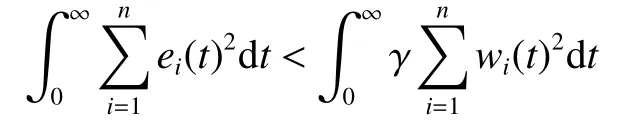
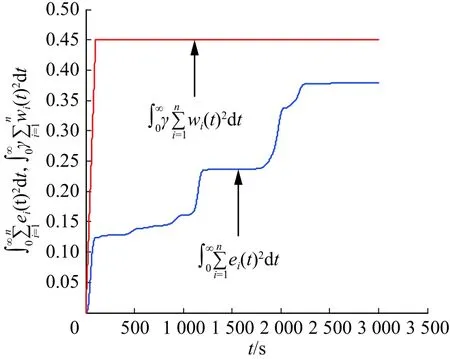
Fig.8 The energy trajectories of and

即滿足 H∞同步。

5 結束語

本文針對一類不確定分數階神經網絡系統，本文研究了其自適應 H∞同步與參數辨識問題。注意到，不確定項總是存在于實際的神經網絡中，而文中所得研究結果可以很好的解決這一問題，即可以精確地對不確定參數項進行辨識同時具有很強的魯棒性。因而，本文的研究結果具有很強的實際應用價值，可以廣泛的應用于實際神經網絡。

然而，本文所考慮的是理想化的網絡模型，在實際應用中，時滯總是存在于神經元之間的通訊過程中，并對系統的穩定性產生嚴重的影響，進而影響對未知參數的辨識精度。注意到，目前還沒有關于此方面比較好的研究結果，因此，有必要設計相關的控制協議來抵消時滯對系統穩定性造成的影響。在未來的研究中，我們將進一步針對帶有時滯的不確定分數階神經網絡，設計相關的控制協議，從而對系統中的未知參數進行精確地辨識，同時使系統實現同步。