Kiselev 黑洞的熱力學性質和物質吸積特性*
魏益煥
(渤海大學數理學院物理系,錦州 121000)
(2018 年11 月19 日收到; 2019 年1 月2 日收到修改稿)
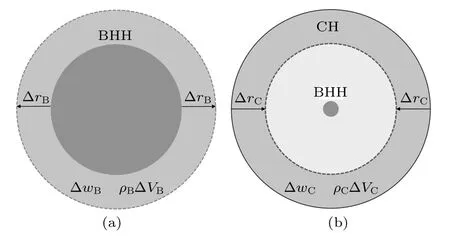
本文考慮帶有黑洞視界和宇宙視界的Kiselev 時空. 研究以黑洞視界和宇宙視界為邊界的系統的熱力學性質. 統一地給出了兩個系統的熱力學第一定律; 在黑洞視界半徑遠小于宇宙視界半徑的情況下,近似地計算了通過宇宙視界和黑洞視界的熱能. 然后,探討Kiselev 時空的物質吸積特性. 在吸積能量密度正比于背景能量密度的條件下給出黑洞的吸積率,討論了黑洞吸積率與暗能量態方程參數的關系.
1 引 言
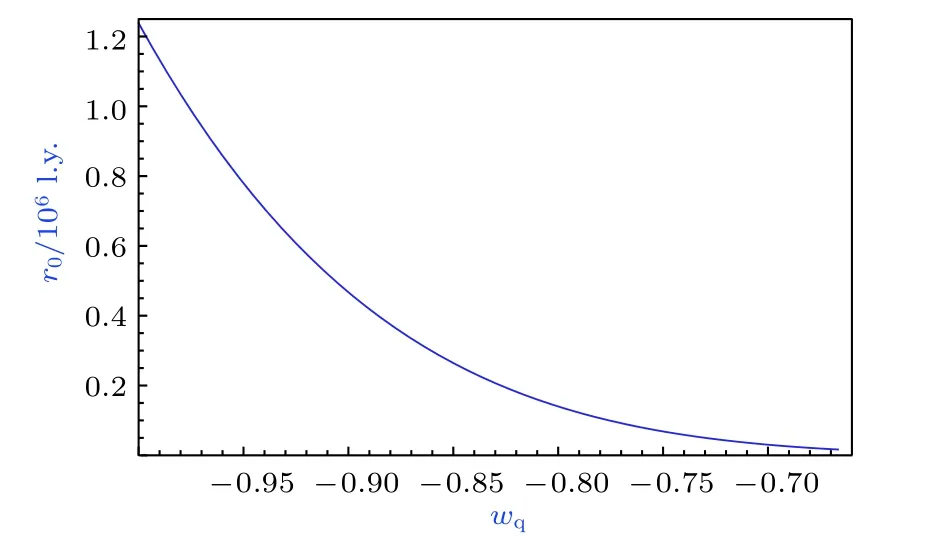
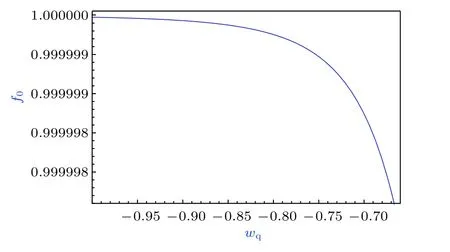
天文觀測表明現在的宇宙正加速膨脹[1?3]. 在愛因斯坦引力中,宇宙的加速膨脹被解釋為宇宙中暗能量的推動. 暗能量可能是Quintessence 能量(Q 暗能量),也可能是其他形式的能量,如真空能等. 所謂的Q 暗能量指宇宙中的正則標量場,它的態方程參數滿足?1 粒子被引力場加速,最終會被天體捕獲,此即所謂的天體吸積現象[7,8]. 對于史瓦西黑洞,其吸積性質類似于牛頓理論中孤立球對稱天體的吸積性質[9]. 黑洞的穩態吸積問題已經得到了廣泛的研究[10?23]. 在wq=?2/3 的情況下,文獻[24]研究了Kiselev 黑洞吸積多方流體的問題. 結果顯示,多方流體的吸積速率和吸積臨界點都與Q 暗能量的能量標度有關. 在文獻[24]中,Kiselev 黑洞被考慮為帶有兩個黑洞視界的黑洞. 對于黑洞周圍存在暗能量的情況,Kiselev 時空存在宇宙視界. 本文研究Kiselev 時空中以黑洞視界和宇宙視界為邊界的時空區域的熱力學性質,探討Kiselev 黑洞對無壓流體物質的吸積特性. 對于時空中存在Q 暗能量的情況,Kiselev 時空度規取下面的形式[4]: 其中λ是具有宇宙尺度的參數,M? λ是黑洞的質量. 該時空有一個黑洞視界(半徑rB)和宇宙視界(半徑rC),其視界半徑近似地為 在上面的計算中,已經使用了條件M?λ. 恒星級質量的黑洞顯然滿足這個條件,即便是超大質量的星系級黑洞,這一條件也成立. 對于宇宙視界,(5)式右邊的第一項是小量,宇宙視界溫度近似為由度規函數f=0 ,得到Kiselev 時空(黑洞)的質量即 其中 (7)式中符號“+”和“–”分別對應到黑洞視界和宇宙視界的情況. 對(6)式兩邊微分得到微分形式的斯馬爾關系 在Kiselev 黑洞斯馬爾關系的表示中,既可采用定義在黑洞視界上的熱力學量,也可采用定義在宇宙視界上的熱力學量. (9)式給出了Kiselev時空的質量增加量與視界熵增加量和參量λ增加量的關系. 球對稱時空(1)中半徑為r的球面內的愛因斯坦準局域能為[25] 將度規函數(2)式代入(10)式給出Kiselev 時空中半徑為r的球面內的能量 宇宙視界附近的能量密度大致正比于Q 能態方程參數的大小,因此具有相同的量級,但黑洞視界附近的能量密度卻隨wq增大而迅速增加(表1). 將r=rB,C代入(10)式得到黑洞視界和宇宙視界內的能量容易驗證,由黑洞視界和宇宙視界包圍的系統滿足熱力學第一定律 其中dQB和 dQC分別是流入黑洞和宇宙視界內的熱量,dwB和dwC分別是時空中的流體對黑洞視界和宇宙視界的功,pB,C=pr(rB,C)和考慮到pB,C=?ρB,C,Kiselev 時空中流體對黑洞視界和宇宙視界的功可寫為 在視界發生微小改變的過程中,時空中流體對視界的功等于視界所掠過時空區域的能量?wB,C=ρB,C?VB,C(圖1). 表1 黑洞視界附近背景時空的能量密度Table 1. Energy density of spacetime near the horizon of black hole. 圖1 (a)黑洞視界做功示意圖; (b)宇宙視界做功示意圖;其中BHH 和CH 分別表示黑洞視界和宇宙視界,? rB,C 表示黑洞視界和宇宙視界半徑的微小變化,虛線表示變化后的黑洞視界和宇宙視界Fig. 1. (a) Doing work of black hole horizon; (b) doing work of cosmic horizon. BHH and CH stand for the black hole horizon and the cosmic horizon,respectively. ? rB,C denotes a small change of the radii of black hole horizon and cosmic horizon. The dotted lines represent the changed black hole horizon and the changed cosmic horizon. 在靜態球對稱時空中,沿徑向運動的流體四維速度是利用歸一化條件uμuμ=?1 ,得到流體四維速度的第0 分量其中xμ=(t,r,θ,φ) . 其中u=u1. 物質的四維流矢量定義為Jμ=nuμ,其中n是流體的粒子數密度. 四維流守恒律=0給出[24] 其中CJ?=0 是常數. 對于流向引力中心的流體,有CJ <0. 理想流體的四維能量-動量張量取如下形式: 其中ρm和pm分別代表流體的能量密度和壓強. 流體四維能量-動量張量守恒方程的零分量方程為 即 其中C1是常數. 對于pm>?ρm的情況,積分常數C1<0 . 方程uν=0 給出[12]對(21)式積分得到 這里C2<0 是積分常數. 若吸積流體是無壓的物質,則(22)和(17)式是同一方程. 由(20)和(22)式得到 對(23)式求導給出 2uu′=?f′,其中f′=df/dr.對于u=0 ,u′=0指f′=0. 方程f′=0 給出Kiselev時空度規函數取極大值的位置r0(圖2), 其中u0=u(r0) 為流體的最大速度. (25)式右邊的f0是f在黑洞視界和宇宙視界間的最大取值 在r=r0附近,Kiselev 時空幾乎是平直時空(圖3).在r=r0處,粒子應該有極小速率 (|u0|?1) . 在這一 假 設 下,有+f0≈f0≈1和C2≈C1=C.在接近黑洞視界處(f≈0 ),流體四維速度的徑向分量uB近似地為?1 . 圖2 在M=10?2 l.y.和λ=1.378×1010 l.y.條件下的r0-wq曲線Fig. 2. Ther 0-wq curve (M=10?2 l.y. andλ=1.378×1010 l.y.). Kiselev 黑洞對無壓理想流體的吸積率為 C=ρmBuBmB=ρm(rB) 其中常數 ,能量密度 . 黑洞視界附近的流體四維速度uμ的徑向分量近似為?1 ,常數C僅依賴黑洞視界半徑和吸積流體的能量密度. 假定黑洞視界附近被吸積流體的能量密度與背景能量密度成正比ρmB=ηBρB,則黑洞的吸積率為 被吸積流體的能量密度對時空背景的影響是微小的,因此要求比例系數ηB?1. 對應于wq=?2/3和wq=?1 ,分別有最大吸積率χmax≈1.2×10?6ηB和最小吸積率χmin≈1.2×10?8ηB(圖4). 上面的討論是在假定參數ηB不依賴wq的情況下進行的.假定ηB隨wq足夠緩慢地改變,則黑洞的吸積率會隨wq的增大而增大. 圖3 在M=10?2 l.y.和λ=1.378×1010 l.y.條 件下的f0-wq 曲線,對 于和? 1 ,分 別 有f 0 ≈0.999998 和0.99999998Fig. 3. Thef 0-wq curve (M=10?2 l.y. andλ=1.378×1010l.y.). For and? 1 ,the metric functionf0 ≈0.999998 and 0.99999998,respectively. 在M? λ的情況下,Kiselev 時空中的流體對宇宙視界所做的功和流入宇宙視界的熱量近似地為和在?1 圖4 黑洞吸積率χ B (單位η B)與w q的關系圖(M=1 0?2 l.y.和λ=1.378×1010 l.y.)Fig. 4. Relationship between black hole accretion rateχB(unitηB) andw q(M=10?2 l.y.andλ=1.378×1010 l.y.). 現在宇宙中約 1 /3 和 2 /3 的部分為物質和暗能量. 宇宙加速膨脹要求宇宙有效態方程參數weff0; 而在r02 Kiselev 時空的熱力學性質
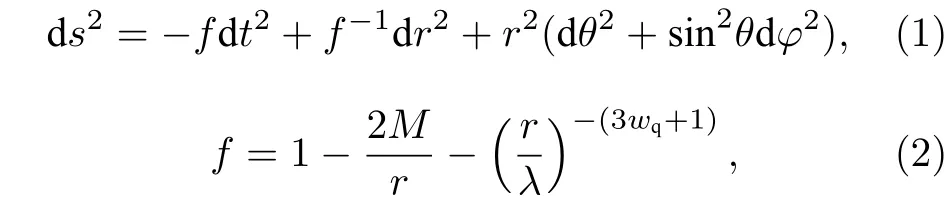
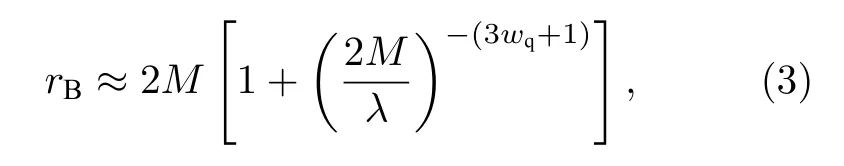
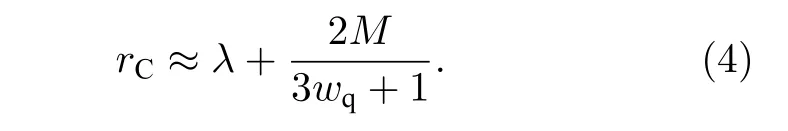
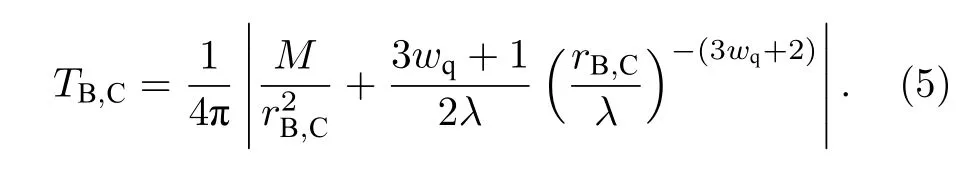
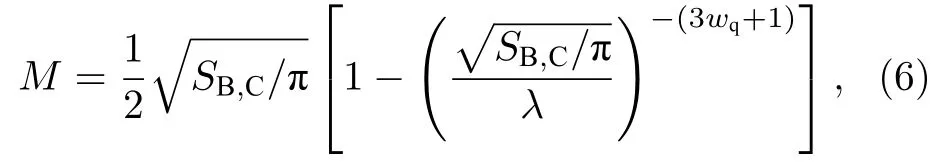
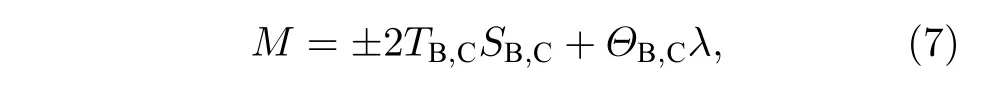
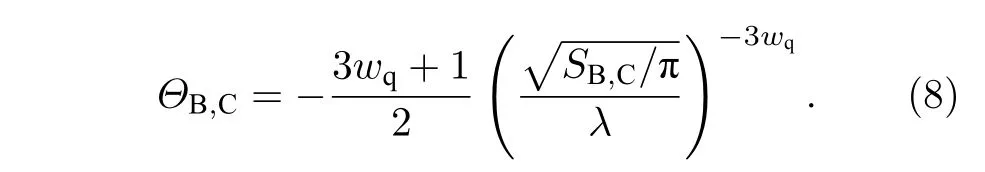
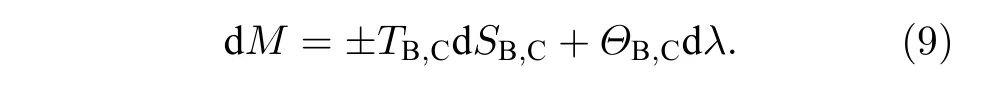
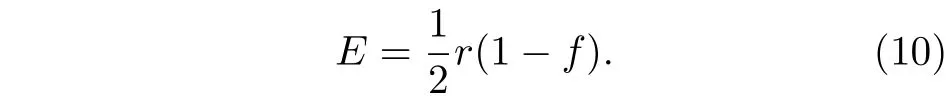
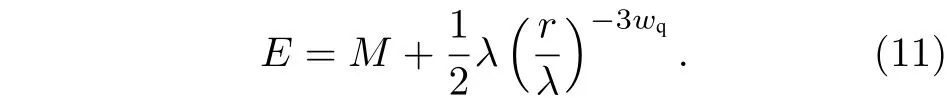
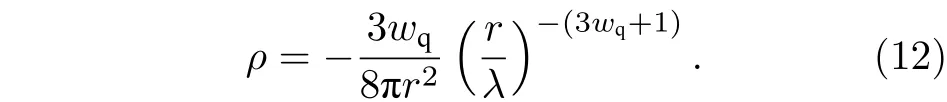
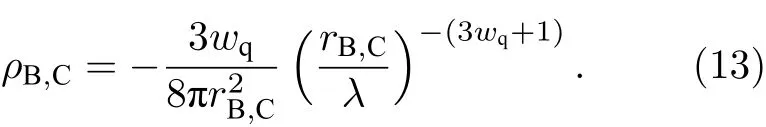
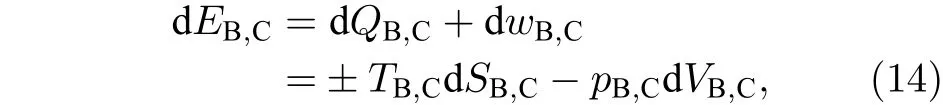
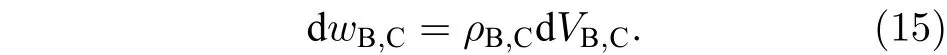

3 Kiselev 時空的物質吸積特性
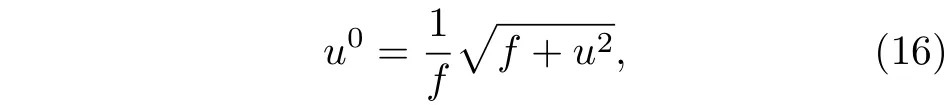
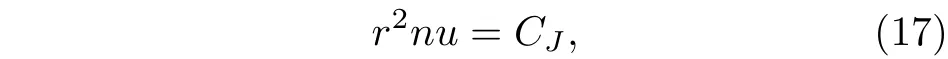
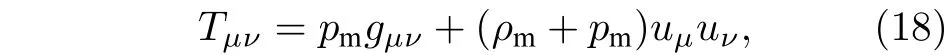
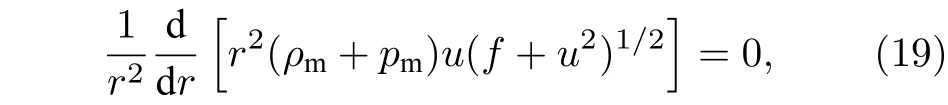
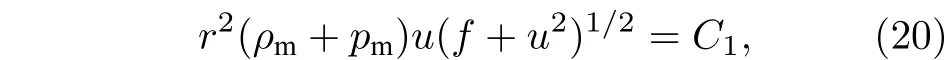
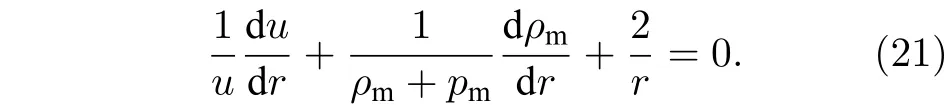
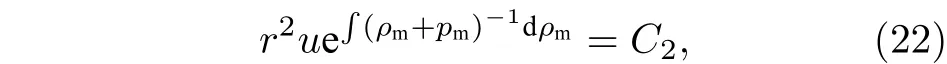
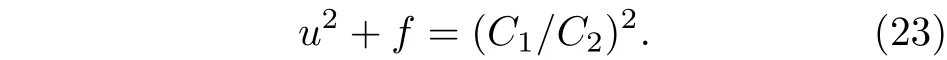
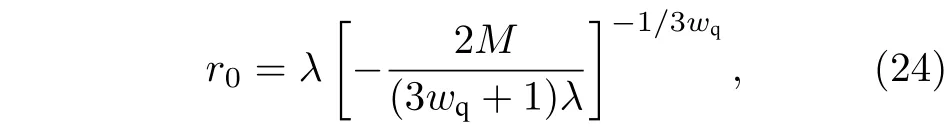
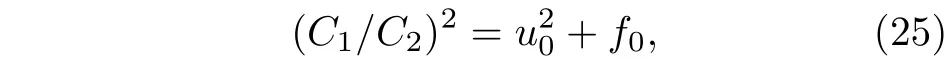
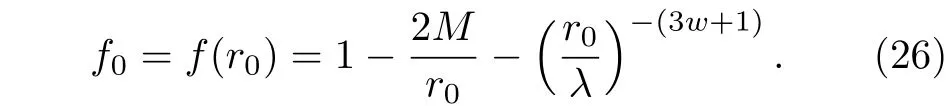
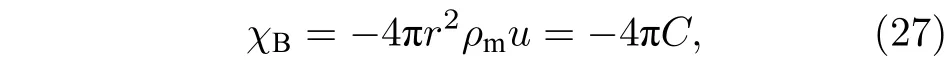
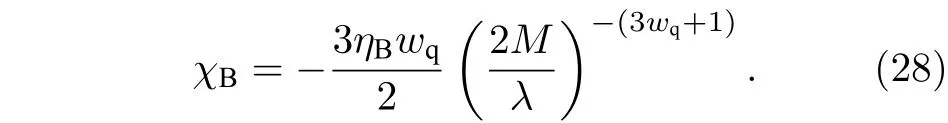
4 結論與討論