洛侖茲破缺標量場的霍金隧穿輻射*

楊樹政 林愷

1) (西華師范大學物理與空間科學學院,南充 637002)

2) (中國地質大學(武漢)地球物理與空間信息學院,地球內部多尺度成像湖北省重點實驗室,武漢 430074)

3) (Escola de Engenharia de Lorena,Universidade de Sao Paulo,12602-810,Lorena,Sao Paulo,Brazil)

(2018 年11 月19 日收到; 2019 年1 月7 日收到修改稿)

把洛侖茲破缺的標量場方程推廣到彎曲時空中,并通過Aether-like 項對標量場方程進行修正,該項所產生的效應也會影響到黑洞時空視界附近處的物理效應. 接著,進一步在半經典近似下得到了修正的Hamilton-Jacobi 方程,然后用這一修正的Hamilton-Jacobi 方程研究了史瓦西黑洞的隧穿輻射特征,并討論了洛侖茲破缺對黑洞霍金輻射和黑洞熵的影響. 結果表明,形式的Aether-like 項的效應可能使黑洞溫度增加,而黑洞熵降低. 該工作可以幫助我們更深刻地理解彎曲時空中的洛侖茲破缺效應的物理性質.

1 引 言

經典的黑洞是全黑的,因為沒有任何經典粒子可以從經典黑洞內穿越出來達到無窮遠的觀測者處. 但是,當霍金考慮了黑洞視界附近的量子效應后,他發現黑洞可以發出量子輻射,這種輻射被稱為霍金輻射[1,2]. 霍金輻射的存在使得黑洞熱力學定律有了牢固的物理基礎,因此把引力理論、量子理論和熱力學及統計理論有效地聯系起來[3?5]. 一個解釋霍金輻射的簡明理論是隧穿理論: 把黑洞視界視為一個勢壘,經典粒子無法直接通過此勢壘,但是由于量子隧穿效應的存在,黑洞視界內部的虛粒子有一定概率穿越黑洞視界這個勢壘,并進一步實化為實粒子,這就是量子霍金輻射. 利用量子隧穿的觀點,文獻[6—14]提出隧穿輻射方法來計算黑洞溫度和熵,隨后文獻[15,16]提出半經典的方法從彎曲時空的標量場方程推導出彎曲時空的Hamilton-Jacobi 方程,并用這個方程計算霍金輻射,這個方法大大簡化了黑洞輻射的研究. 2008 年,Kerner 和Mann[17,18]開始思考用半經典的方法研究Dirac 場粒子的隧穿輻射,在這個方法中,他們把Dirac 粒子分為自旋向上和自旋向下兩種情況,并進一步推導得到Dirac 粒子的隧穿輻射方程[19?24].本課題組[25?27]則提出新的方法來研究費米子隧穿輻射問題,在我們的方法中,Dirac 方程先通過半經典近似化為一個簡明的矩陣方程,這個方程可以通過gamma 矩陣寫成一個很簡單的形式,接著根據gamma 矩陣的反對易特性,發現半經典的矩陣方程成立的條件正是標準的Hamilton-Jacobi 方程,接著按照標準的半經典Hamilton-Jacobi 方法可以推導出黑洞的費米子隧穿輻射特征. 該結果暗示了Hamilton-Jacobi 方法的內在一致性,其本質是體現了理論的洛侖茲對稱性.

然而,在高能領域的研究中,量子引力的研究暗示洛侖茲不變性可能需要在普朗克尺度上被修正. 近來,一種洛侖茲破缺的標量場理論被提出,其作用量可以寫為[28]

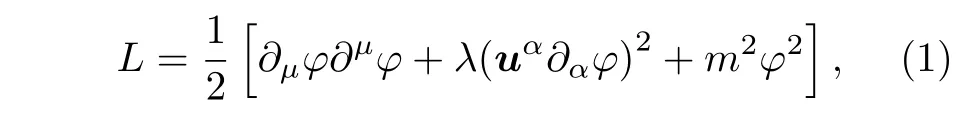
其中m是標量場的質量;λ是洛侖茲破缺項的比例常數,通常是一個小量;uα在平直時空中是一個類以太場的常矢量,本文將始終使用(–,+,+,+)的號差. 因此在平直時空中修正的標量場方程變為

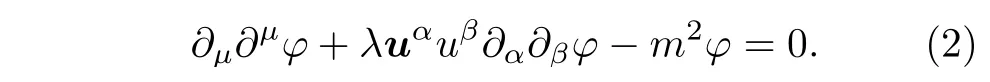
近來的工作對這種修正的標量場方程進行了深入探討[28?32],發現在高能領域修正的標量場方程有許多獨特的性質.

本文把洛侖茲破缺的標量場方程的工作進一步推廣到彎曲時空,并進一步研究黑洞的霍金輻射. 在第2 節中,將首先給出彎曲時空中的洛侖茲破缺標量場方程,并進一步通過半經典近似把該方程化為變形Hamilton-Jacobi 方程; 接著在第3 節中,將具體計算在史瓦西時空背景下的修正的霍金輻射特征,得到修正的標量場隧穿輻射和修正的霍金溫度; 第4 節給出討論和結論.

2 洛侖茲破缺的標量場方程以及修正的Hamilton-Jacobi 方程

在正則坐標系的平直時空中類以太矢量是一個常量,因此自然滿足關系

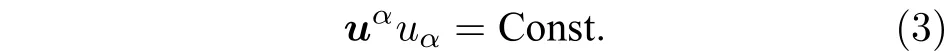
但是在彎曲時空中,為了滿足(2)式的關系,不能簡單把uα設為常量. 因此在彎曲時空中,考慮作用量

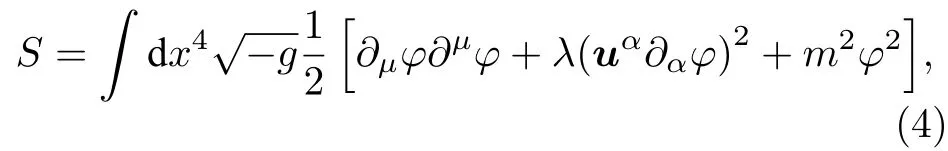
可以得到彎曲時空中的洛侖茲破缺標量場方程為

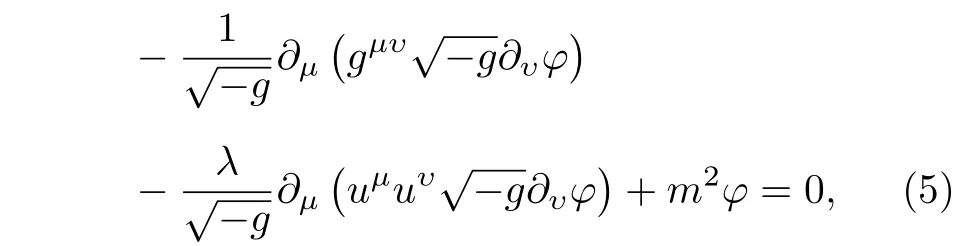
或者

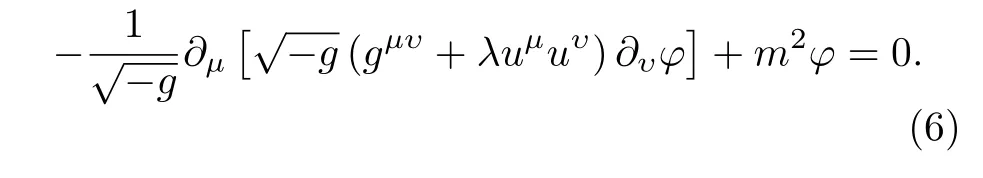
為了得到彎曲時空中的修正Hamilton-Jacobi方程,可以重寫標量場波函數為

根據(3)式可以求得

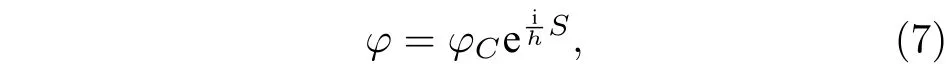
所以把(7)式代入任意自旋的玻色子方程,把 ? 視為小量,并且只保留方程的零階項,可以得到

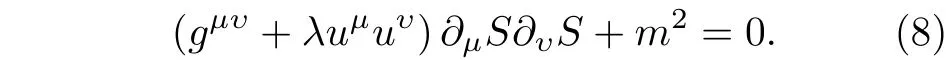
這正是修正的標量場粒子的Hamilton-Jacobi 方程. 第3 節將應用這個半經典的修正Hamilton-Jacobi 方程研究黑洞的霍金輻射特征.

3 史瓦西黑洞的隧穿輻射及其修正

史瓦西黑洞的逆變度規可以寫為

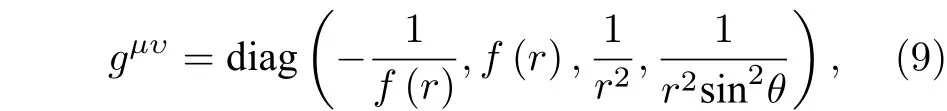
其中

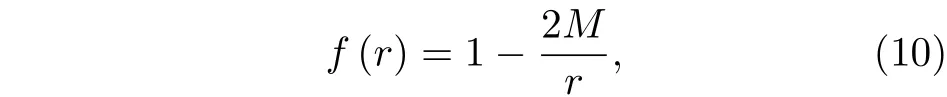
其中M是黑洞的質量,黑洞視界rh=2M. 這里分別討論四種情況下的黑洞輻射. 由于作用量S可以寫為

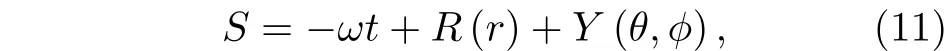
于是(8)式可以寫為

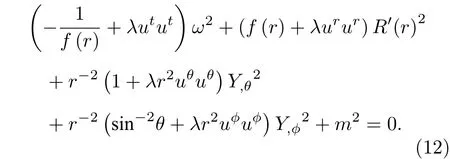
為了求解上述方程,先考慮不同的uα情況:

1)uα=(ut,0,0,0) 情況這里c0是一個常數. 因此,通過(12)式可以把徑向的Hamilton-Jacobi 方程寫為

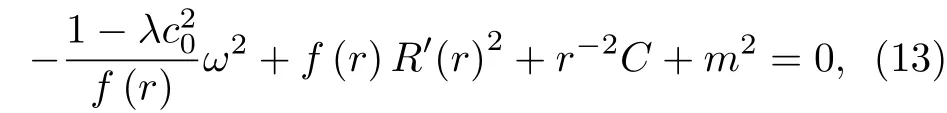
這里的C是分離變量常數,因此有

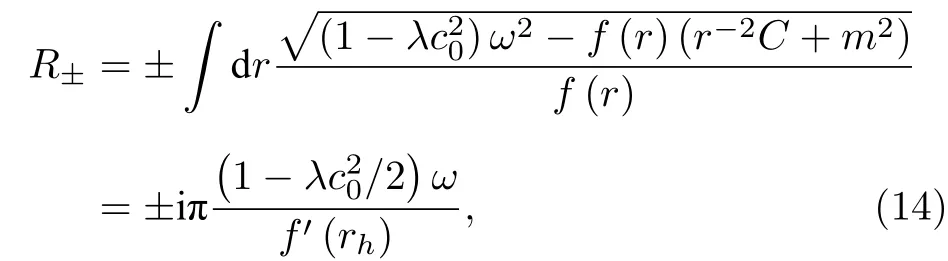
這里正負號分別代表出射模和入射模,在計算中,已經用到λ是小量的條件. 所以黑洞的隧穿輻射率是

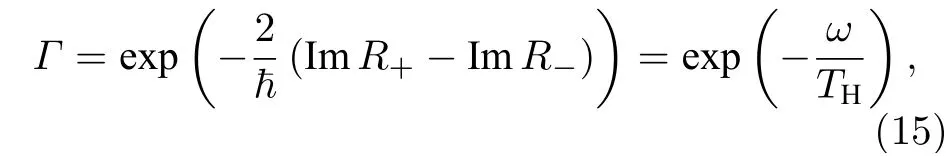
其中,霍金溫度是

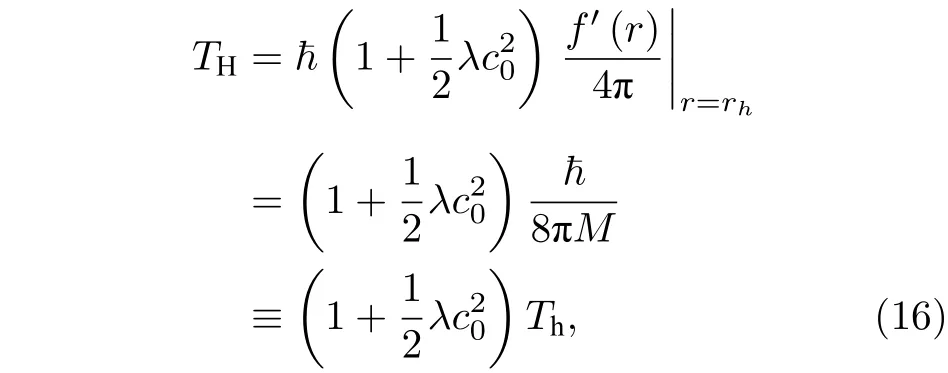
這里的Th是未修正的史瓦西黑洞事件視界處的霍金溫度,而修正后的霍金溫度TH則與/2 相關.

2)uα=(0,ur,0,0)情況

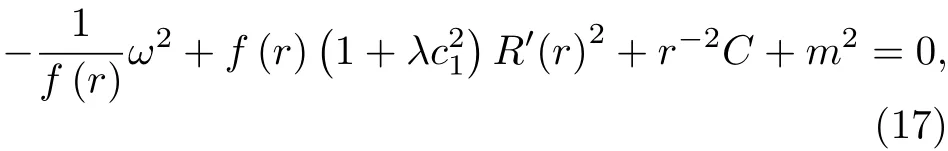
這里的C也是分離變量常數,因此有

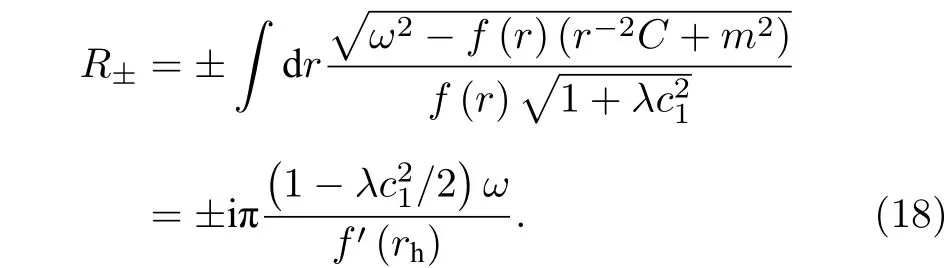
黑洞的隧穿輻射率依然是(15)式的形式,但是其中霍金溫度是

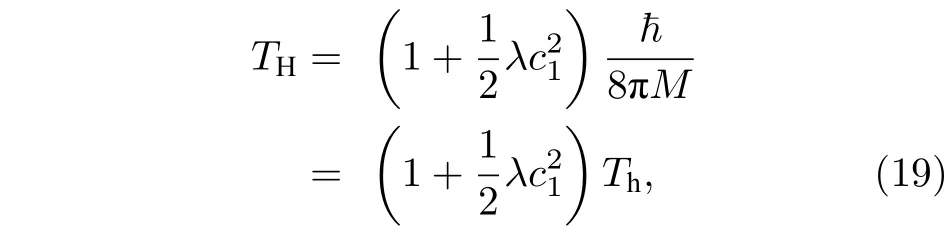
在這里修正后的霍金溫度TH也與相關.

4 結 論

另一方面,黑洞熱力學中另一個重要的物理量是黑洞的熵,修正的霍金溫度也會帶來黑洞熵的修正. 根據黑洞熱力學有

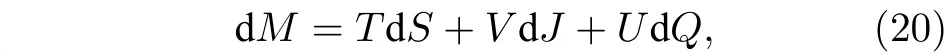
其中V和U分別是黑洞的旋轉勢和電磁勢. 因此,在事件視界rh處未修正之前的黑洞熵滿足

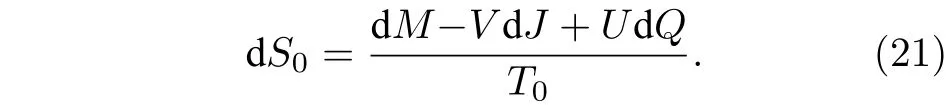
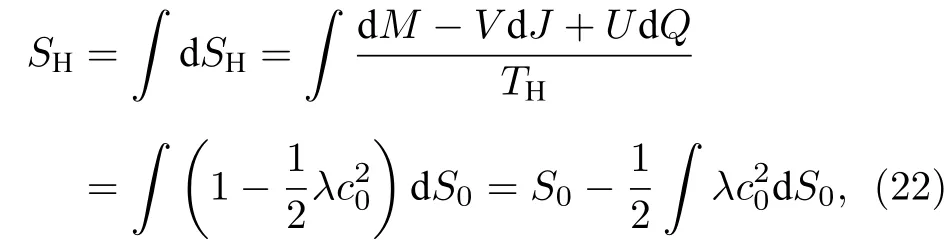
而在uα=的情況中,黑洞熵為

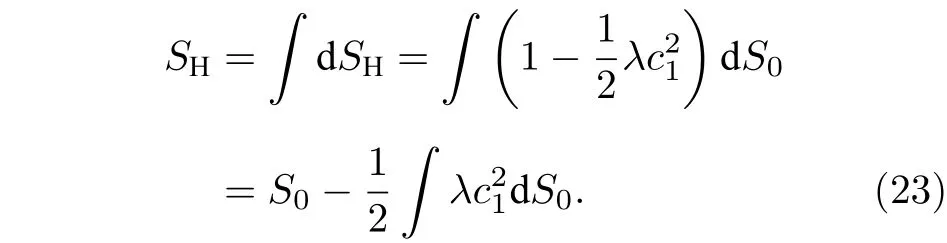
所以如果λ是一個正數,uα=和uα=的情況將導致黑洞的熵減小.

本文研究的是最簡單的修正標量場情況,近來越來越多的高能物理研究傾向于認為洛侖茲對稱性在高能尺度下會產生破缺,人們已經陸續提出各種洛侖茲破缺的量子場方程. 這些研究可能為將來量子引力的研究提供有力的支持. 在彎曲時空中,黑洞表面簡單而極端的性質可能成為將來驗證洛侖茲破缺理論的有力工具. 我們將繼續研究關于彎曲時空中洛侖茲破缺的量子場論.