復合式襯砌隧道總安全系數設計法修正與應用研究

肖明清， 徐 晨

(中鐵第四勘察設計院集團有限公司， 湖北 武漢 430063)

0 引言

交通隧道常采用復合式襯砌。在復合式襯砌的初期支護計算方法方面，國內外眾多學者進行了深入研究[1-3]，提出了工程類比法、特征曲線法、地層-結構法、基于極限分析的地層-結構法等方法，例如文獻[4]介紹了錨桿的計算方法，但缺少明確的荷載值與安全系數計算； 在二次襯砌計算方面，一般采用荷載-結構法。由于初期支護和二次襯砌采用的計算方法不同，難以統一評價復合式襯砌這一整體結構的安全性。為此，肖明清等建立了復合式襯砌隧道總安全系數設計法[5-6]，并采用該方法分析了鐵路隧道的安全性[7-8]，對錨桿作用、隧道承載主體、支護參數優化等爭議問題進行了研究[9]。

總安全系數設計法的核心內容包括： 1)提出了采用圍巖壓力表征值來解決實際施工中圍巖壓力不確定問題的思路，并提出了圍巖壓力表征值的計算方法，得出了該計算方法具有安全性與經濟性的結論[7，10]； 2)建立了噴層(為便于表述，不管噴射混凝土內是否含有鋼筋網或鋼架，均簡稱為噴層)、錨桿、噴層-錨桿-圍巖組合承載拱3個荷載結構計算模型，用于初期支護的承載能力與安全系數計算[6]； 3)提出了復合式襯砌的總安全系數計算方法，并采用噴層-二次襯砌復合結構承載力計算模型對總安全系數計算方法的合理性進行了分析[9]； 4)提出了總安全系數的取值建議[5-9]。

在以往總安全系數設計法中，噴層、二次襯砌分別按現行隧道設計規范[11-12]采用破損階段法進行截面強度校核； 對于噴層-錨桿-圍巖組合承載拱，由于其為不同材料組成的結構，因此采用應力等效的方法將整個截面等效為T型截面。但由于目前規范中尚沒有偏心受壓狀態下T型截面對應破損階段的安全系數計算方法，因此采取了折中方法進行處理(即取圍巖或噴層極限強度與不同材料截面邊沿應力的比值作為安全系數，且極限強度考慮設計支護力的影響)，這就導致了承載拱安全系數計算方法與噴層、二次襯砌不一致，造成整個方法體系有不合理之處。此外，錨桿采用直接承受圍巖壓力的計算模型對于軟弱圍巖也有不合理之處(錨桿直接承受圍巖壓力主要用于懸吊桿模型，在軟弱圍巖中不適用)。因此，本文對上述不合理之處進行修正，然后采用修正后的設計方法再次分析高速鐵路雙線隧道和20世紀普速鐵路單線隧道的安全性，并與挪威Q法支護參數進行對比，同時結合單線鐵路隧道案例說明該方法的應用。

1 修正后的總安全系數設計法

1.1 圍巖壓力表征值的計算

1.1.1 采用圍巖壓力表征值作為設計荷載的必要性

施工完成后的一定時間內，圍巖壓力在某個具體位置為定值并作為恒載處理，但由于地質條件的千變萬化、施工水平的差別、支護參數的不同，即使圍巖條件相同，圍巖壓力在時空上也具有變異性，具有活載的特性。采用安全系數設計法時，荷載及組合應采用最不利工況，因此需要尋找圍巖壓力的最不利情況。為此，可以引入圍巖壓力表征值作為支護結構的設計荷載，來解決真實荷載難以確定的問題。需要說明的是，圍巖壓力表征值不是作用于支護上的實際值，只是一個用于結構計算的荷載名義值。顯然，圍巖壓力表征值應具備安全性與經濟性2個特征，即： 既要能夠包絡可能的最大圍巖壓力，又不能過于保守而影響經濟性。

1.1.2 建議采用的深埋隧道圍巖壓力表征值計算方法

1.1.2.1 當埋深(H)不小于10～15倍洞徑(D)時

當H≥(10～15)D時，對于符合摩爾-庫侖強度準則的圍巖，圍巖壓力表征值的計算公式如下。

豎向均布荷載：q=αγ(Rpd-a)。

(1)

水平均布荷載：e=βλq。

(2)

(3)

式(1)—(3)中：α、β分別為拱部和側部圍巖壓力調整系數，一般不小于1.2，同時根據圍巖產狀等因素進行調整(如水平巖層，α可取大于1.0的系數，β可取小于1.0的系數)；γ為圍巖重度；Rpd為pi=0時，θ=45°位置處隧道塑性區半徑，pi為支護力，θ為塑性區半徑取值位置與隧道橫軸的夾角；a為當量圓圓心至45°位置處隧道開挖邊界的距離；λ為圍巖側壓力系數；R0為隧道開挖半徑，斷面非圓形時取當量圓半徑；p0為圍巖初始應力，自重應力場為主時，p0=γH；c為圍巖黏聚力；φ為圍巖內摩擦角。

式(3)為魯賓涅特方程[2]，式(4)為著名的卡斯特納方程[2]。當λ=1.0時，式(3)的計算結果與式(4)相同； 當λ≠1.0時，式(3)在θ=45°位置處隧道塑性區半徑也與式(4)計算結果相同，但式(3)中的p0應取水平應力與豎直應力的平均值。

(4)

1.1.2.2 當埋深小于10～15倍洞徑時

當H<(10～15)D時，按上述公式得到的結果誤差較大，建議采用實際埋深下的彈塑性有限元方法求解無支護時的塑性區范圍，并取拱部90°范圍內的平均塑性區高度作為圍巖壓力表征值的等效高度。為保證安全，也可直接采用H=(10～15)D時的公式計算值。

1.1.2.3 深埋短區段軟弱圍巖的壓力修正

當較差圍巖的兩端為較好圍巖時，受空間效應的影響，實際圍巖壓力表征值要低于公式計算值，具體折減值與埋深、隧道洞徑、較差圍巖長度等因素有關。當Ⅴ級圍巖兩側為Ⅳ級圍巖，且圍巖分界面與隧道軸線垂直時，采用三維有限元模型得出的400 m埋深Ⅴ級圍巖壓力表征值(無支護開挖，取Ⅴ級圍巖中間位置拱頂90°范圍內的平均塑性區高度作為Ⅴ級圍巖壓力表征值的等效高度)與式(3)計算值的比值ξ見圖1[10]。

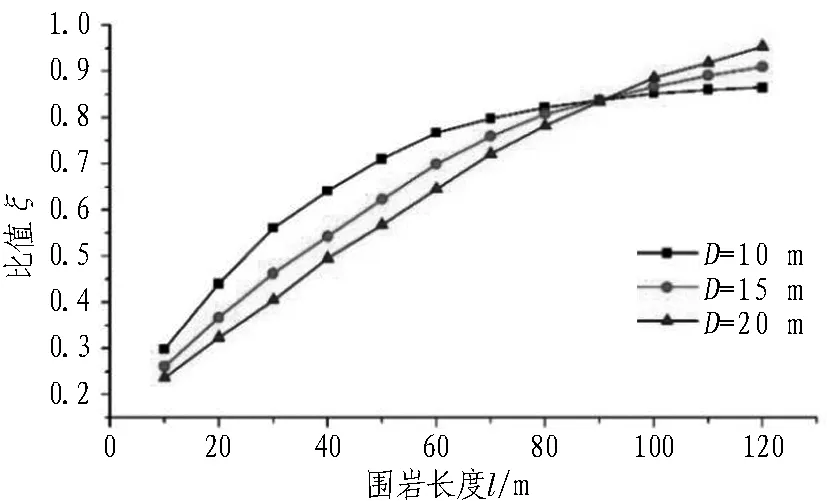
圖1 Ⅴ級圍巖長度、洞徑對圍巖壓力表征值的影響

Fig. 1 Influence of length of grade V surrounding rock and tunnel diameter on representative value of surrounding rock pressure

由圖1可知： 當圍巖長度l較小時，其圍巖壓力表征值可以大幅度折減。此外，如果軟弱圍巖采取了超前注漿，則加固圈具有明顯的承載作用，也可以顯著降低圍巖壓力表征值。經計算，當隧道洞徑為15 m、Ⅴ級圍巖的加固圈厚度為3 m、加固體強度為2 MPa時，圍巖壓力表征值可減少70%～75%。

1.2 復合式襯砌的荷載結構模型

復合式襯砌一般由噴錨支護、二次襯砌以及中間的防水層組成，相應的在總安全系數設計法中，有噴層的計算模型(模型1)、錨桿-圍巖承載拱計算模型(模型2)、錨桿的計算模型(模型3)、二次襯砌的計算模型(模型4)4個模型。其中，模型1、2、4的荷載均取圍巖壓力代表值。

1.2.1 初期支護方案

初期支護一般有以下3種方案。

支護方案1： 無系統錨桿支護結構，即初期支護主要由噴層組成，不設置系統錨桿，僅設置局部錨桿防止施工期掉塊。

支護方案2： 噴錨組合支護結構，即初期支護由噴層和系統錨桿共同組成。

支護方案3： 以錨為主的支護結構，即圍巖壓力全部由系統錨桿-圍巖承載拱承擔，錨桿之間的局部松散荷載由薄的噴層承擔。

1.2.2 模型1(噴層的荷載結構模型)

模型1中(見圖2)，噴層采用梁單元模擬，結構與地層相互作用采用無拉徑向彈簧和切向彈簧模擬。求得噴層的內力后，結構安全系數K1按現行隧道設計規范[11-12]采用破損階段法進行計算； 當噴層內設置了鋼架、鋼筋網時，可按鋼筋混凝土或型鋼-混凝土組合結構計算。噴層作為結構層的最小厚度不宜小于8 cm[3]。

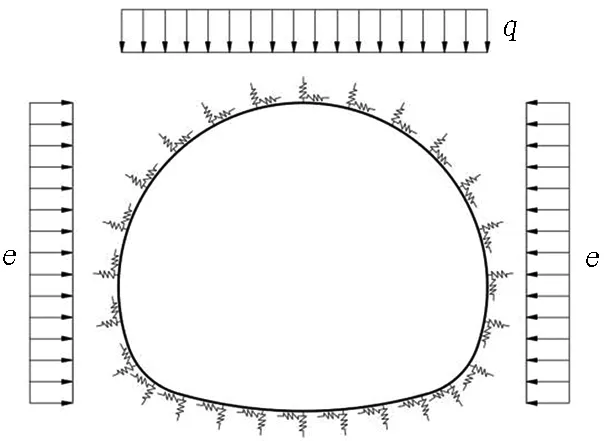
圖2 模型1(噴層的荷載結構模型)

1.2.3 模型2(錨桿-圍巖承載拱計算模型)

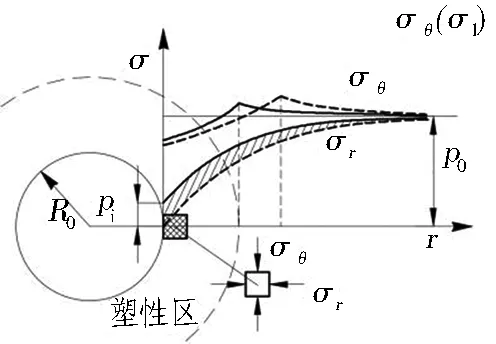
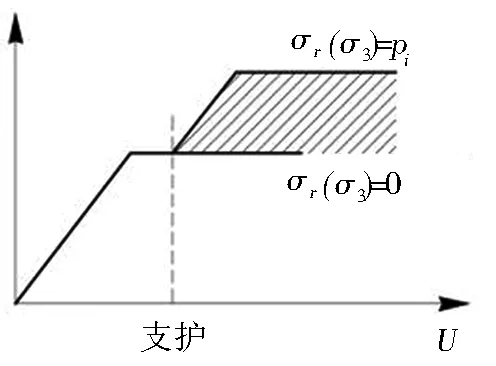
隧道開挖后，周邊一定深度范圍內的圍巖進入塑性狀態，無法承擔后續增加的荷載，如圖3所示。當采取噴層、錨桿等措施進行支護后，可增加塑性區圍巖的側限，進而增加圍巖繼續承載的能力。按此機制，可得出錨桿-圍巖承載拱的計算模型見圖4。

(a) (b)

σr為徑向力，σθ為切向力，σ1為最大主應力，σ3為支護為圍巖提供的支護力。

圖3塑性區圍巖在支護力作用下的承載機制

Fig. 3 Bearing mechanism of surrounding rock in plastic zone under supporting force

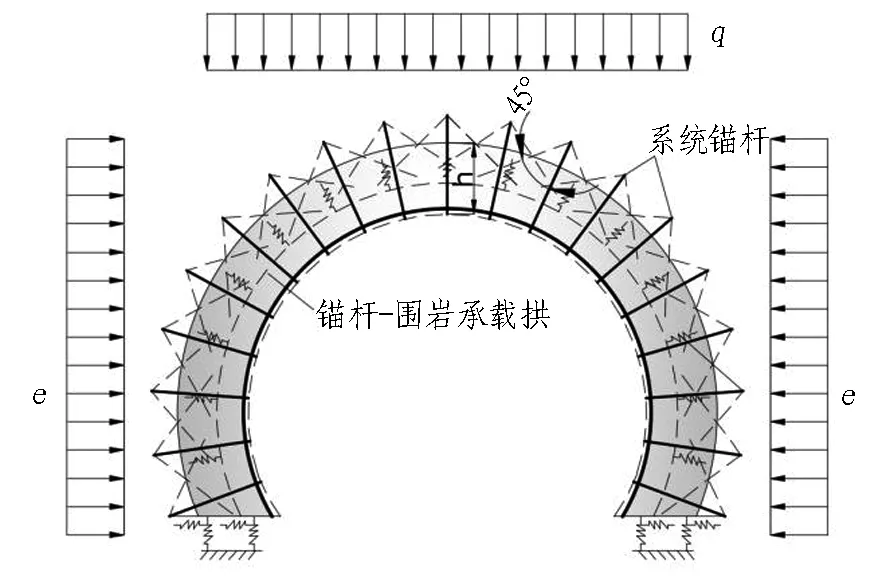
圖4 模型2(錨桿-圍巖承載拱的荷載結構模型)

Fig. 4 Model 2 (load-structure model of bolt-surrounding rock bearing arch)

模型2中(見圖4)，錨桿的外端頭按一定角度(如45°)向隧道內側進行壓力擴散，相鄰錨桿壓力擴散后的交點所形成的連線即為承載拱的外邊線； 承載拱內邊線為噴層外表面。承載拱采用梁單元模擬，采用徑向彈簧模擬圍巖與承載拱的相互作用，拱腳處采用彈性支撐，其余參數(如彈性模量、黏聚力、內摩擦角等)按勘察資料或現行規范選取。

求得承載拱的內力后，其安全系數K2按現行隧道設計規范采用破損階段法進行計算。但承載拱范圍內圍巖的極限強度僅考慮支護后增加的強度，即： 將錨桿、噴層、二次襯砌提供的支護力作為σ3(計算詳見1.2.4節)，進而根據摩爾-庫侖強度準則得出圍巖的σ1，此σ1即作為極限強度(當混凝土的極限應變小于σ1與圍巖彈性模量之比時，應將二者的比值作為σ1的折減系數)。在施工期σ3由σ31(錨桿提供)、σ32(噴層提供)組成，施工期安全系數記為K2c； 在運營期σ3由σ31(錨桿提供)、σ32(噴層提供)和σ33(二次襯砌提供)組成，運營期安全系數記為K2op。

1.2.4 模型3(錨桿的計算模型)

錨桿的設計參數(長度、間距、直徑)需結合模型2計算，并根據支護類型采用不同的方法。

1.2.4.1 采用噴錨組合支護時錨桿的計算模型

采用噴錨組合支護時，錨桿主要為模型2的承載拱提供部分側限力(即σ3的一部分，σ3的另一部分由噴層、二次襯砌提供)，錨桿長度根據承載拱受力要求確定，錨桿的間距與直徑(強度)根據需要其提供的側限力進行計算(如圖5所示)，且桿體本身的屈服強度安全系數不宜小于2.0，抗拔安全系數不宜小于2.5。

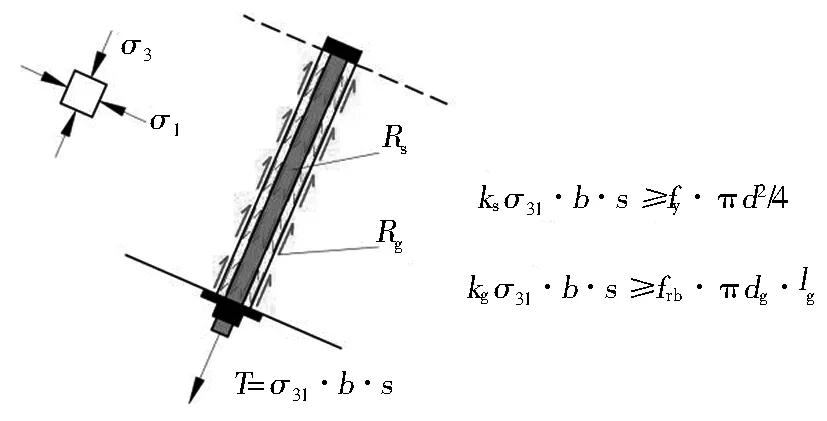
Rs為錨桿鋼筋的承載力；Rg為孔道灌漿料(砂漿錨固體)與巖體之間的黏結力；T為錨桿軸力；ks為錨桿的屈服承載力安全系數；kg為錨桿的抗拔安全系數；σ31為錨桿提供的側限力；fy為錨筋鋼材的屈服強度；d為錨筋直徑；frb為砂漿錨固體與地層間的極限黏結強度；dg為砂漿錨固體的外徑；lg為錨筋與砂漿的錨固長度；b、s分別為錨桿的環向間距和縱向間距。

圖5模型3(錨桿的荷載結構模型)

Fig. 5 Model 3 (load-structure model of bolt)

需說明的是，σ3由σ31(錨桿提供)、σ32(噴層提供)、σ33(二次襯砌提供)組成，施工階段可不計入σ33，σ32和σ33可近似按以下公式計算。

σ32=0.5K1·q；

(5)

σ33=0.5K3·q。

(6)

式(5)—(6)中K1、K3分別為噴層、二次襯砌的安全系數。

1.2.4.2 采用以錨為主支護時錨桿的計算模型

當采用以錨為主的支護時，錨桿強度(屈服強度以及抗拔承載力)除滿足承載拱受力所需的σ3要求外，還需滿足最小支護力的要求。

文獻[1]提出了最小支護力的估算方法： 當λ=1時，圓形隧洞圍巖松動區內滑裂面為1對對數螺線，假設松動區內強度已大大下降，可認為滑移巖體已無自承作用以致于其全部質量由支護力pi，min來承擔(如圖6所示)，由此有：

(7)

式中Rmax為與pi，min相對應的松動區半徑。

圖6 最小支護力的計算圖示

由切向應力σθ=P0確定松動半徑Rmax：

(8)

由式(7)、式(8)聯立可以解出最小支護力。

1.2.5 模型4(二次襯砌的計算模型)

二次襯砌的計算模型與模型1基本相同，但由于噴層與二次襯砌之間的防水層不傳遞剪力，故防水層設置區域二次襯砌與圍巖的相互作用僅采用無拉徑向彈簧模擬(見圖7)，安全系數K3采用破損階段法計算。

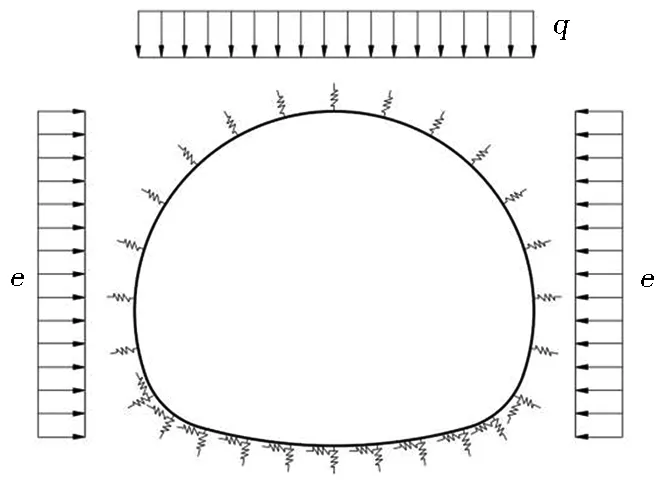
圖7 模型4(二次襯砌的荷載結構模型)

1.2.6 不同支護方案計算模型的選擇

1.2.1節所述3種初期支護方案可分別采用上述計算模型進行計算。

對于支護方案1，噴層的結構組成(噴混凝土、鋼架、鋼筋網等)、材料選擇與尺寸參數等僅可采用模型1計算。

對于支護方案2，噴層可采用模型1計算； 錨桿的長度、間距、強度可采用模型2、模型3計算。此外，模型2中噴層提供σ32需要采用模型1的計算結果。

對于支護方案3，錨桿的長度、間距可采用模型2計算，錨桿材質、直徑、抗拔所需長度可采用模型3計算。

對于二次襯砌，僅可采用模型4計算，但其強度對模型2的安全系數有影響。

1.3 復合式襯砌總安全系數計算方法與取值

1.3.1 復合式襯砌總安全系數計算方法

由上述初期支護方案及各計算模型可知，復合式襯砌的承載結構由2層(承載拱+二次襯砌、噴層+二次襯砌)或3層(承載拱+噴層+二次襯砌)組成。假設每層結構均為線彈性結構，且其中一個結構層的某一截面先達到極限強度時可以繼續保持該強度，直至各層結構均達到極限強度時才出現完全破壞，則按上述方法分別計算噴層、錨桿-圍巖承載拱、二次襯砌的安全系數后，復合式襯砌的總安全系數可以近似計算如下(K2在施工期和運營期分別采用K2c和K2op表示)。

施工階段(無二次襯砌)：Kc=K1+K2c。

(9)

運營階段，

采用耐久性錨桿：Kop=K1+K2op+K3。

(10)

采用非耐久性錨桿：Kop=K1+K3。

(11)

需說明的是，理論上在相同總安全系數的前提下可以有多種支護參數方案。由于不同支護方案中各層結構并非總是同時達到最不利截面強度，因此按公式(9)—(11)得到的總安全系數是整體結構的最小安全系數，實際承載能力一般會高于上述計算結果(詳見1.3.3節)。同時，該計算方法也為整體結構的優化設計提供了一個目標函數，最為經濟的結構應是實際承載能力接近總安全系數計算值，并根據造價、可實施性等因素進行選擇。

1.3.2 總安全系數取值

建議運營階段總安全系數Kop≥3.0～3.6，施工階段(無二次襯砌)噴層、錨桿-圍巖承載拱的總安全系數Kc≥1.8～2.1[5-6]。總安全系數可以根據結構重要性、圍巖具體條件以及施工質量控制等因素進行調整。

1.3.3 噴層-二次襯砌復合結構的分析

錨桿-圍巖承載拱位于整體結構的最外層，即使全部進入塑性狀態，只要噴層與二次襯砌未出現整體失穩，則該結構不會單獨失穩。因此，需要對噴層-二次襯砌復合結構的承載能力進行分析。

1.3.3.1 破壞階段噴層-二次襯砌復合結構的承載能力分析模型

噴層與二次襯砌共同承載的復合結構計算模型如圖8(a)所示，二者之間法向彈簧的剛度

(12)

式中：E1、E2分別為噴層、二次襯砌的彈性模量；h1、h2分別為噴層、二次襯砌的厚度；A為接觸單元的面積。

當噴層或二次襯砌的某個截面達到破損階段，假設其可以維持破損階段的承載力，并將破損區域的內力作為邊界條件施加在破損位置，再繼續增大荷載直至結構整體破壞，其計算模型如圖8(b)和圖8(c)所示(分別對應大偏心受壓破壞和小偏心受壓破壞)。

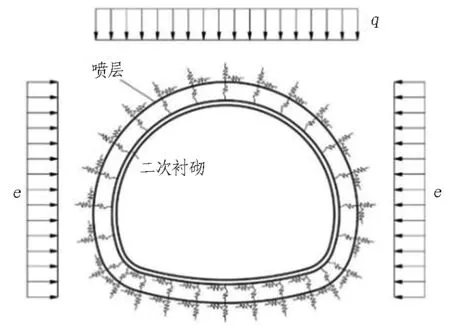
(a) 計算模型

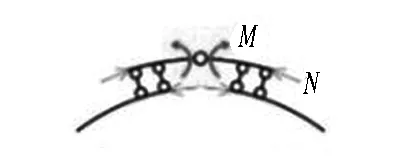
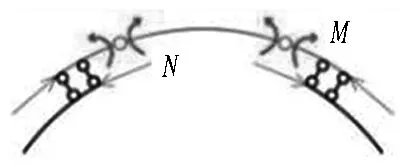
(b) 大偏心受壓破壞 (c) 小偏心受壓破壞

M為彎矩，N為軸力。

圖8噴層-二次襯砌復合結構承載力計算模型

Fig. 8 Bearing capacity calculation model of shotcrete layer-secondary lining composite structure

1.3.3.2 復合結構破壞次序對承載力的影響

根據噴層與二次襯砌的破壞次序，復合結構(不含錨桿-圍巖承載拱)整體破壞階段的荷載比例系數Kd(即通過加大荷載值來使結構破壞的破壞荷載與設計荷載的比值，其內涵與安全系數不完全相同)與總安全系數法計算結果的對比可分為以下3種情況。

第1種： 當噴層與二次襯砌同時達到最不利截面強度，則Kd=K1+K3。

第2種： 當噴層先于二次襯砌達到設計強度，但由于二次襯砌位于其外側，噴層不會整體失穩，可以繼續承載，直至二次襯砌最不利截面達到破損階段，此時Kd>K1+K3。

第3種： 二次襯砌先于噴層達到最不利截面強度，需要二次襯砌第一破損區繼續發展或形成新的破損區時噴層才能達到破損階段，此時Kd>K1+K3。

對于第3種情況，由于二次襯砌有多個破損區，雖然可以繼續承載，但可能會超出正常使用對適用性的要求(如對于高鐵隧道，拱墻部位的破損區可能因列車振動作用而發生掉塊)，因此應通過斷面形狀的調整或噴層與二次襯砌強度的匹配來控制二次襯砌第一破損區的位置，使之不出現在拱墻部位； 對于第2種情況，也應合理控制噴層與二次襯砌的強度匹配，防止因噴層破壞區過大而使二次襯砌出現突然的脆性破壞。綜上所述，合理的設計方案應是噴層與二次襯砌基本同時達到最不利截面強度，其荷載比例系數Kd基本等于或略高于K1+K3； 當高出K1+K3較多時，應調整設計參數或斷面形狀。

同理，也可建立錨桿-圍巖承載拱、噴層、二次襯砌3層結構的整體承載力模型，但由于K2是基于噴層、錨桿、二次襯砌的破損階段得出的，隨著模型1、3、4達到破壞狀態而達到最大值，因此3層結構實際上可以簡化為圖8所示的2層結構。同樣，需要使荷載比例系數Kd基本等于或略高于K1+K2+K3。

2 既有隧道的安全性計算分析

以高速鐵路雙線隧道通用參考圖和20世紀90年代編制的時速140 km單線電氣化鐵路隧道標準圖為例，采用總安全系數設計法對其安全性進行計算分析。相關結構斷面、支護參數與材料性能等分別見文獻[5-8,13]。

2.1 時速350 km高速鐵路雙線隧道通用參考圖的安全性分析

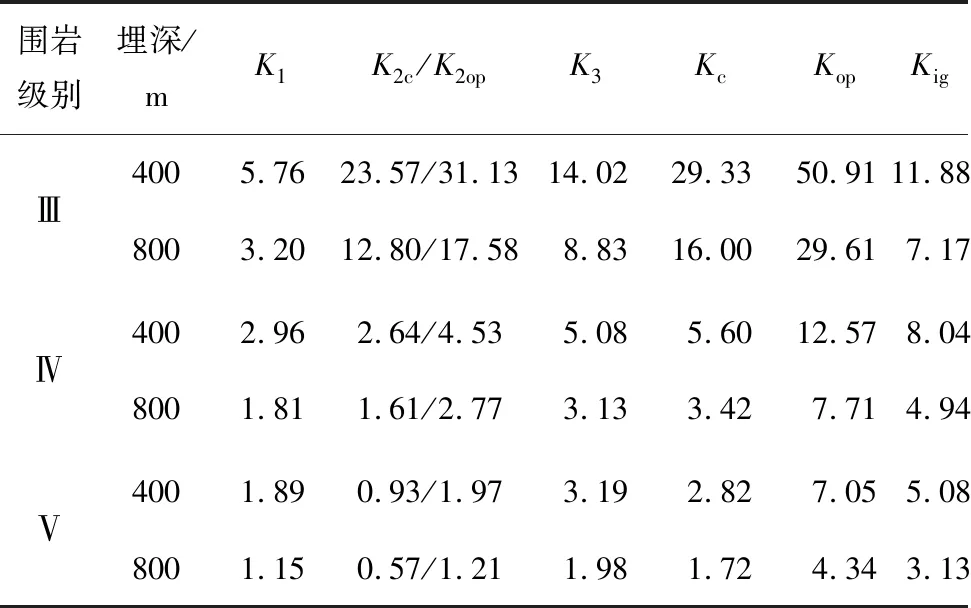
表1為所分析案例的安全系數計算結果(表中Ⅴ級圍巖的荷載已考慮空間效應與注漿因素進行了折減，其取值為Ⅳ級圍巖的1.8倍，下同)。由表1可知： 1)Ⅴ級特大埋深(800 m)的安全系數最接近最小安全系數要求(略高出最小安全系數3.0)，是最為經濟的結構；其余情況的安全系數均偏高，具有一定的優化空間。2)施工期不考慮錨桿的作用時(對應實際施工中部分工點省略系統錨桿的情況)，除Ⅴ級特大埋深外，其余各種情況僅依靠噴層就可以提供足夠的安全系數來保證圍巖穩定，不僅間接說明了本計算與實際基本符合，也說明了支護參數具有優化的空間(即只要保證錨桿質量，就可以減少噴層強度)。

表1時速350 km高速鐵路雙線隧道安全系數

Table 1 Safety factors of 350 km/h high-speed double-track railway tunnel

圍巖級別埋深/mK1K2c/K2opK3KcKopKigⅢⅣⅤ4005.7623.57/31.1314.0229.3350.9111.888003.2012.80/17.588.8316.0029.617.174002.962.64/4.535.085.6012.578.048001.811.61/2.773.133.427.714.944001.890.93/1.973.192.827.055.088001.150.57/1.211.981.724.343.13

注：Kig表示忽略錨桿作用時的安全系數，下同。

2.2 時速140 km單線電氣化鐵路隧道標準圖的安全性分析

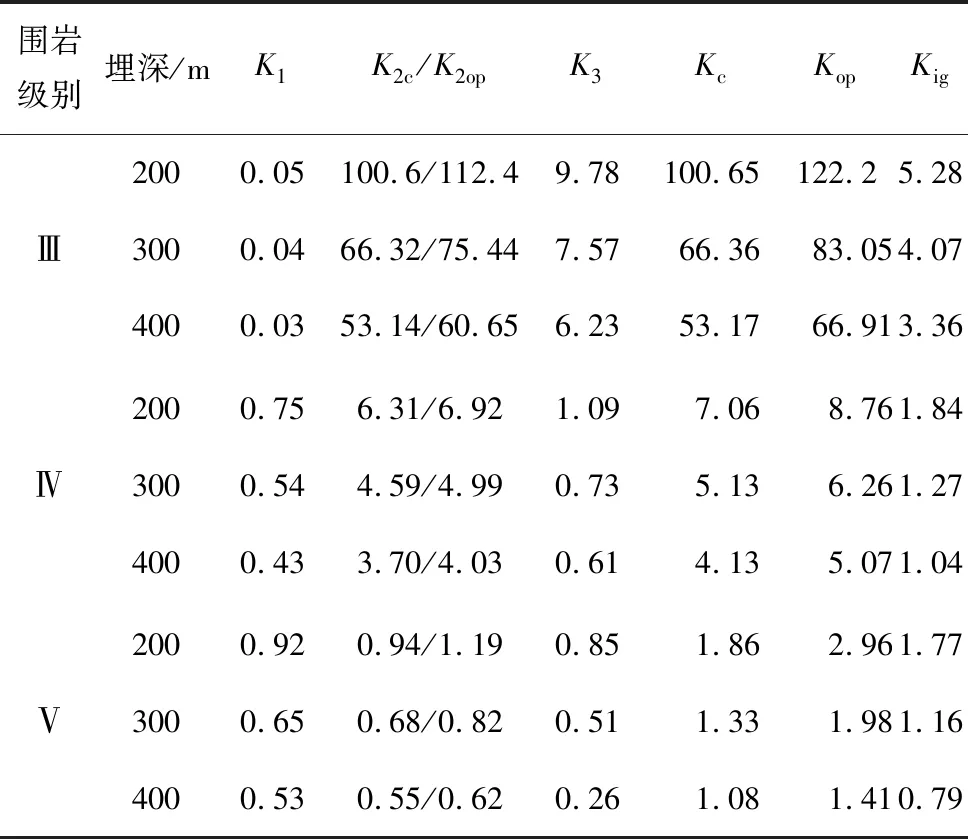
表2為所分析案例的安全系數計算結果。由表2知： 1)該支護參數在Ⅳ、Ⅴ級圍巖地段的運營期總安全系數偏低(不考慮錨桿耐久性)，特別是錨桿-圍巖承載拱所提供的安全系數在總安全系數中的占比較大，而所采用的錨桿并非耐久性錨桿，因此結構開裂的可能性隨運營時間的延長會加大，需要特別關注(安全系數偏低，意味著失效概率增加)。文獻[14]指出，既有鐵路隧道病害問題日益突出，據統計，約有70%隧道存在滲漏水現象，且在2002年以前的運營鐵路隧道中襯砌裂損病害較嚴重，可見本文計算結果與既有隧道病害較為普遍的現狀基本相符。2)該標準圖中說明了其適用埋深不宜大于300 m，由本文計算結果可知，當埋深達到400 m時，Ⅳ、Ⅴ級圍巖地段的安全系數偏低，說明支護參數與埋深相對應的設計方法是合理的。

表2時速140 km單線電氣化鐵路隧道安全系數

Table 2 Safety factors of 140 km/h electric single-track railway tunnel

圍巖級別埋深/mK1K2c/K2opK3KcKopKigⅢⅣⅤ2000.05100.6/112.49.78100.65122.25.283000.0466.32/75.447.5766.3683.054.074000.0353.14/60.656.2353.1766.913.362000.756.31/6.921.097.068.761.843000.544.59/4.990.735.136.261.274000.433.70/4.030.614.135.071.042000.920.94/1.190.851.862.961.773000.650.68/0.820.511.331.981.164000.530.55/0.620.261.081.410.79

3 與挪威Q法的支護參數對比

20世紀90年代，挪威學者Barton提出了著名的Q法[15]，在世界各地得到了廣泛應用。一般認為，Q法支護參數是比較經濟的，為分析其安全性并與總安全系數法相互驗證，以時速350 km高速鐵路雙線隧道為例對Q法支護參數的安全性進行分析，并對采用與挪威同樣的耐久性錨桿時高鐵隧道復合式襯砌可能的一種優化支護參數進行計算。計算時，Ⅲ、Ⅳ、Ⅴ級圍巖分別采用規范中物理力學指標范圍值的下三分之一分位值。根據不同埋深，本文估算了所采用圍巖參數對應的Q值，并根據文獻[15]列出了相應的支護參數，相關計算結果見表3。

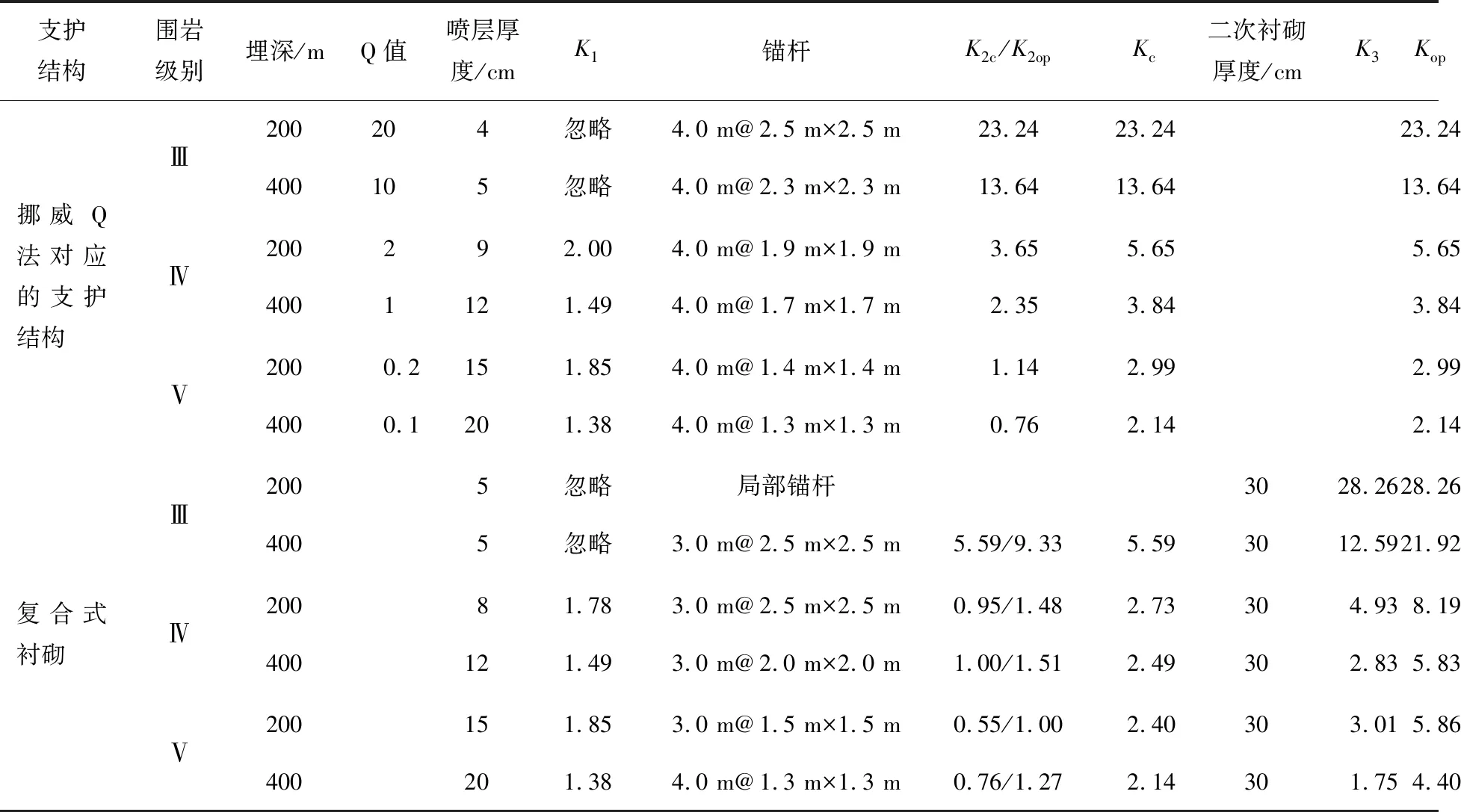
表3 支護參數與安全系數計算結果

注： 1)表中錨桿均采用M33-CT耐久性錨桿，承載力為345 kN； 2)本次計算噴層采用C30噴射混凝土，二次襯砌采用C30素混凝土； 3)Q法不設置二次襯砌，故K2c=K2op。

由表3可知： 1)Q法支護參數用于我國高鐵雙線隧道時，Ⅲ、Ⅳ級圍巖總安全系數滿足本文提出的建議值要求且較為經濟，但Ⅴ級圍巖安全系數偏低； 2)采用復合式襯砌時，如果二次襯砌采用30 cm C30素混凝土，則初期支護僅需滿足施工期的安全系數要求，與Q法相比可以減弱錨桿參數； 3)采用耐久性錨桿有利于充分發揮錨桿-圍巖承載拱的永久支護作用，與既有通用圖支護參數相比，可以減少噴層和二次襯砌的強度，提高經濟性。

4 總安全系數法在隧道斷面形式比選中的應用

采用工程類比法設計時，無法得出不同斷面形式對安全性的影響； Q法支護參數選擇考慮的斷面因素主要是隧道跨度或高度，也無法體現斷面形式的差異。為了進一步說明總安全系數設計法的應用，以時速160 km單線鐵路隧道為例來說明斷面形式與支護參數的比選。

4.1 隧道斷面形式與支護參數方案

對時速160 km單線鐵路隧道擬定了2種斷面形式(見圖9)、3種支護參數方案，3種支護方案在Ⅴ級圍巖條件下的支護參數見表4。方案1開挖寬度為8.34 m，高度為10.15 m，高跨比為1.22，如圖9(a)所示； 方案2開挖高度與方案1相同，但開挖寬度增加1 m，高跨比變為1.09，如圖9(b)所示。方案1、方案2采取相同的支護參數，方案3斷面形式與方案2相同，但根據總安全系數法對支護參數進行了調整，擬定了400 m和800 m埋深的2種支護參數。

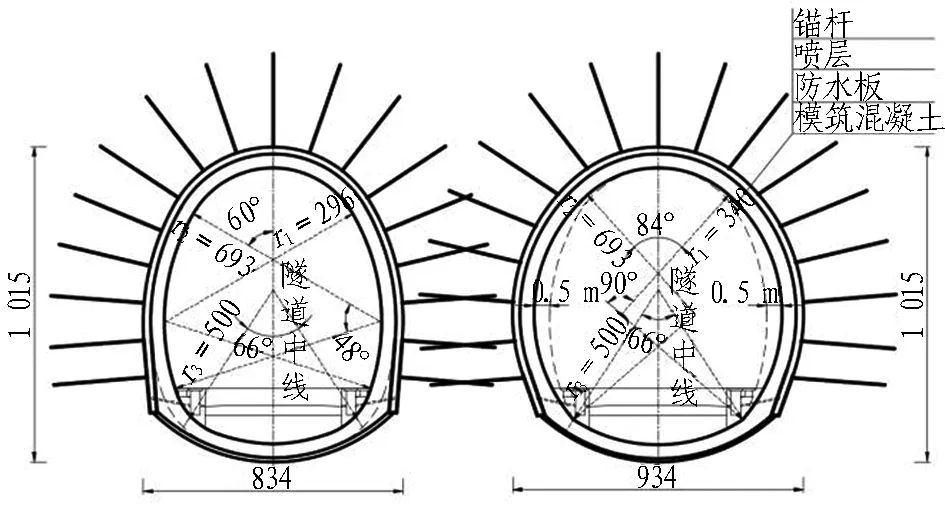
(a) 方案1 (b) 方案2

Fig. 9 Two cross-section forms of 160 km/h single-track railway tunnel (unit: cm)

4.2 安全系數計算結果

計算所得的安全系數如表5所示。由表5可知： 1)方案2與方案1相比，支護參數相同，但高跨比由1.22減少至1.09，支護的總安全系數大幅提高，說明斷面形式對安全系數具有顯著影響； 2)方案1與方案2的初期支護安全系數均偏低，無法滿足施工期安全系數要求，需要及時施作二次襯砌； 3)方案3在方案2的基礎上，根據埋深設置了不同的支護參數，在總安全系數滿足要求的前提下，減小了二次襯砌的安全冗余并提高了初期支護的安全系數，具有更為合適的安全性與經濟性。

表4 時速160km單線鐵路隧道支護參數

表5時速160 km單線鐵路隧道3種方案安全系數

Table 5 Safety factors of 160 km/h single-track railway tunnel under three schemes

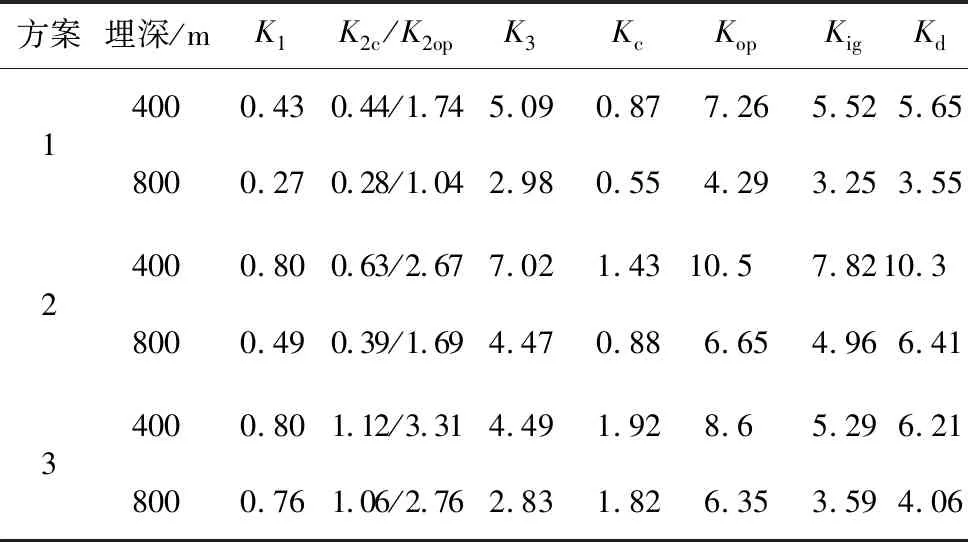
方案埋深/mK1K2c/K2opK3KcKopKigKd1234000.430.44/1.745.090.877.265.525.658000.270.28/1.042.980.554.293.253.554000.800.63/2.677.021.4310.57.8210.38000.490.39/1.694.470.886.654.966.414000.801.12/3.314.491.928.65.296.218000.761.06/2.762.831.826.353.594.06

4.3 噴層-二次襯砌復合結構的承載力分析

采用噴層-二次襯砌復合結構承載力模型分析表明，3種方案噴層均先于二次襯砌破壞，噴層為墻腳區域小偏心受壓破壞。方案1的二次襯砌破壞位置位于墻腳區域，為大偏心受壓； 方案2與方案3的二次襯砌破壞位置位于邊墻，為小偏心受壓，說明斷面調整改善了結構的受力狀態。

表5示出噴層-二次襯砌復合結構破壞階段的荷載比例與噴層、二次襯砌的總安全系數對比結果，可以得出： 1)方案1和方案3(2種支護方案)復合結構整體破壞階段的荷載比例系數Kd僅略高出K1+K3(分別高出2%～9%、17%、13%)，說明噴層與二次襯砌具有較好的強度匹配關系； 2)方案2總安全系數過高，且整體破壞階段的荷載比例系數Kd比K1+K3高出較多(29%～32%)，說明初期支護與二次襯砌的匹配不合理，主要是二次襯砌過強，需要優化； 3)安全系數相加的方法為整體結構的優化設計提供了一個目標函數，并可通過噴層-二次襯砌復合結構承載力模型進行具體驗證與優化。

5 結論與建議

1)提出了采用圍巖壓力表征值作為設計荷載的思路，可以解決設計中圍巖壓力不確定的問題。當H≥(10～15)D時，對于符合摩爾-庫侖強度準則的圍巖，可以采用式(1)—(3)計算圍巖壓力表征值；當H<(10～15)D時，為安全考慮，可以直接采用H=(10～15)D時的公式計算值。當較差圍巖的兩端為較好圍巖時，圍巖壓力表征值需要考慮空間效應進行折減，具體折減值與埋深、隧道洞徑、較差圍巖段的長度等因素有關。此外，如果軟弱圍巖采取超前注漿，則加固圈具有明顯的承載作用，也可以顯著降低圍巖壓力代表值。

2)建立了復合式襯砌各支護層(噴層、錨桿-圍巖承載拱、二次襯砌)的荷載結構模型與安全系數計算方法，提出了施工期、運營期總安全系數計算方法與取值，提出了噴層-二次襯砌雙層結構以及承載拱-噴層-二次襯砌3層結構的破壞次序與總承載力分析模型，可用于各支護層的安全性校核、強度匹配與參數優化。所建立的總安全系數設計法能夠體現錨桿-圍巖承載拱、噴層、二次襯砌各自的承載作用與承載能力，為初期支護和復合式襯砌的支護構件選擇、量化設計以及多層結構的整體優化設計提供了一定的理論基礎。

3)對時速350 km高速鐵路雙線隧道通用參考圖和20世紀90年代編制的時速140 km單線電氣化鐵路隧道標準圖的安全系數計算結果表明，總安全系數設計法得出的結論與現場實際施工情況、既有隧道病害情況基本相符。

4)與挪威Q法支護參數的對比表明，Q法的支護參數如用于我國時速350 km高速鐵路雙線隧道，Ⅲ、Ⅳ級圍巖滿足本文提出的總安全系數建議值要求且較為經濟，但Ⅴ級圍巖安全系數偏低。當采用與Q法相同的耐久性錨桿時，所得出的高鐵雙線隧道支護參數與現行通用參考圖有較大差別。采用耐久性錨桿有利于充分發揮錨桿-圍巖承載拱的永久支護作用，從而可以減少噴層和二次襯砌的強度，提高經濟性。

5)對時速160 km單線鐵路隧道斷面形式與支護參數的研究表明，總安全系數設計法可以用于隧道斷面形式與支護參數的精細比選，克服了工程類比法和Q法等方法不能體現隧道斷面形式差異的缺點。

需說明的是，本文所建立的總安全系數設計法尚缺少室內試驗和現場驗證的支撐，特別是錨桿-圍巖承載拱的承載能力與安全系數計算方法需要進一步的試驗研究。此外，如果噴層-錨桿-圍巖作為一個整體結構(等效T型截面)進行計算，相比本文應該更為合理，但目前規范中尚沒有偏心受壓狀態下T型截面對應破損階段的安全系數計算方法，還有待進一步試驗研究。