一種含閉環支鏈的新型并聯機構設計與分析

房海蓉, 王立, 張海強, 楊會

(北京交通大學機械與電子控制工程學院 機器人研究中心, 北京 100044)

目前，航天飛行器殼體多為復合材料加工而成的大直徑薄壁筒狀結構，因此在與環狀金屬端框的套裝對接的過程中常常發生變形和翹曲，進而產生對接阻力大、工件易損壞、裝配精度差等一系列問題[1-2]。目前，很多大型飛行器的套裝方式為手動施力于螺旋裝置進行推進，常導致工件變形、位姿調整困難、裝配效率低，已經難以滿足現階段的裝配要求，因此需要針對飛行器殼體套裝特點設計一種新型的五自由度位姿調整和推進結構[3]。

航天飛行器殼體的套裝過程要求裝置調整位姿精確，抗阻能力強，因此要求推進機構必須具有剛度大和精度高這2個特點，同時位姿調整的范圍不大，而并聯機構具有剛度大、精度高、響應快的優點[4]，在位姿調整、部件對接等領域應用較多。

針對少自由度并聯機構構型的設計，國內外學者通過螺旋理論[5]、群論[6]、機構拓撲學[7]等方法對3T2R機構進行了構型綜合，如唐衛星[8]、李秦川[9]等，但通過該類方法得出的構型往往支鏈桿件數目過多，結構十分繁雜，難以應用于實際生產應用中。針對上述問題，學者們采用了新的設計方法，可歸納為以下2種：①串并混聯形式，如Song[10]、Dong[11]等在三自由度并聯機構末端串聯兩自由度轉頭，Xu等[12]為三自由度機構增加兩自由度的操作轉臺，該方法有效解決了結構復雜和控制難的問題，但串聯部分結構強度較弱；②在六自由度機構中添加被動支鏈的形式，如劉建坤[13]用CPU支鏈取代一條六自由度支鏈作為主動支鏈，Sun[14]、楊會[15]等直接在機構中間添加約束支鏈作為被動支鏈，Xie等[16]添加被動支鏈并對支鏈結構進行了改進，該方法利用被動支鏈限制了動平臺的自由度，發揮了五自由度機構的優勢，但動平臺的約束力或力偶完全由一條支鏈承擔，需要該支鏈有較高的強度。

本文就如何提高飛行器套裝位姿調整機構的剛度和精度提出了一種新型的5-U(RRP)S/(8U)PU并聯機構，并開展了相關研究。

1 機構結構配置

由于機構對剛度有較高的要求，故以5條六自由度支鏈作為主動支鏈，添加1條五自由度約束支鏈作為被動支鏈，以此作為機構的基本配置方式。

對于主動支鏈，機構設計流程如圖1所示。為提高剛度，在傳統的UPS支鏈上附加一條UPS支鏈并簡化運動副。該方法構造的閉環結構本質是一個五桿機構，因此需要同時添加2個驅動才能保證機構運動的唯一性，這就使得整個機構為冗余驅動并聯機構，增加了質量，也增加了控制難度，違背了支鏈構型的初衷。在該機構的基礎上，將一條支鏈上的移動(P)副舍去，則閉環結構為四桿機構，擁有1個自由度，結合球(S)副及底部的轉動(R)副共擁有5個自由度，因此整個支鏈的自由度數目減少為5。為滿足六自由度，在底部R副處再增加一個R副構成虎克鉸(U)。該閉環三角形支鏈與UPS支鏈相比，極大地提高了機構的穩定性和強度。

被動支鏈結構如圖2所示，底部采用平行六面體結構(以下簡稱8U結構)[17]，頂部為U副和P副，該結構用R副代替P副，使得結構更加緊湊，有效提高了支鏈的強度，同時避免過多的P副產生自鎖。

圖3為新型5-U(RRP)S/(8U)PU并聯機構的三維結構。該機構由動平臺、靜平臺、5條主動支鏈和1條被動支鏈組成。主動支鏈依次由虎克鉸(U)、2個R副、P副和復合S副組成，其中U副與靜平臺相連，每個P副為驅動副，復合S副與動平臺相連；被動支鏈依次由8U結構、P副、U副組成，其中8U結構與靜平臺相連，U副與動平臺相連。靜平臺為等邊五邊形，動平臺為對稱五邊形，該設計可以保證選擇主動支鏈的P副作為驅動副時各主動支鏈的等效運動具有線性無關性。

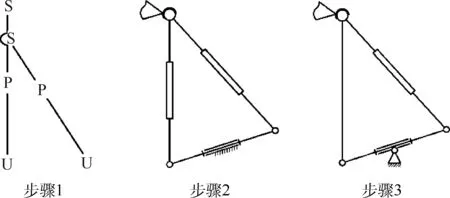
圖1 主動支鏈結構設計流程Fig.1 Design flow of active limb structure

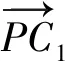
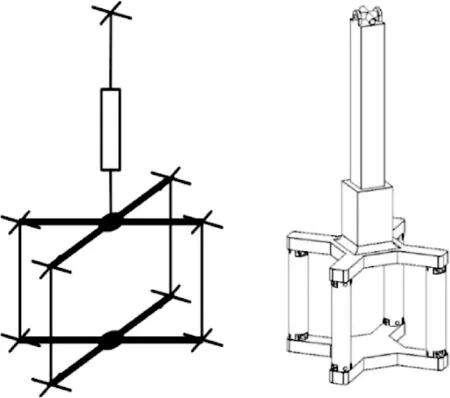
圖2 被動支鏈結構示意圖Fig.2 Schematic of passive limb structure

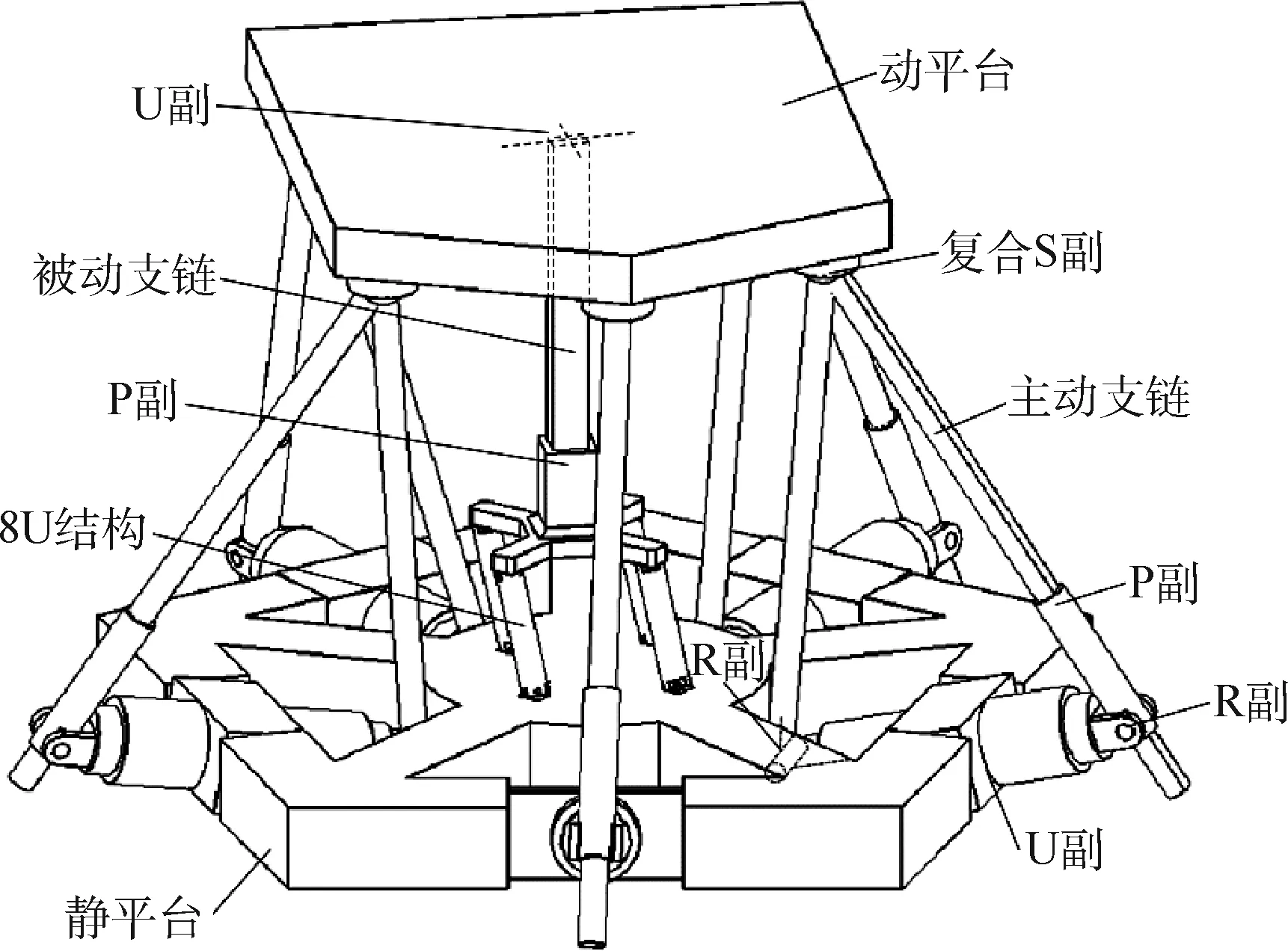
圖3 新型5-U(RRP)S/(8U)PU 并聯機構結構示意圖Fig.3 Schematic of a new type of 5-U(RRP)S/(8U)PU parallel mechanism

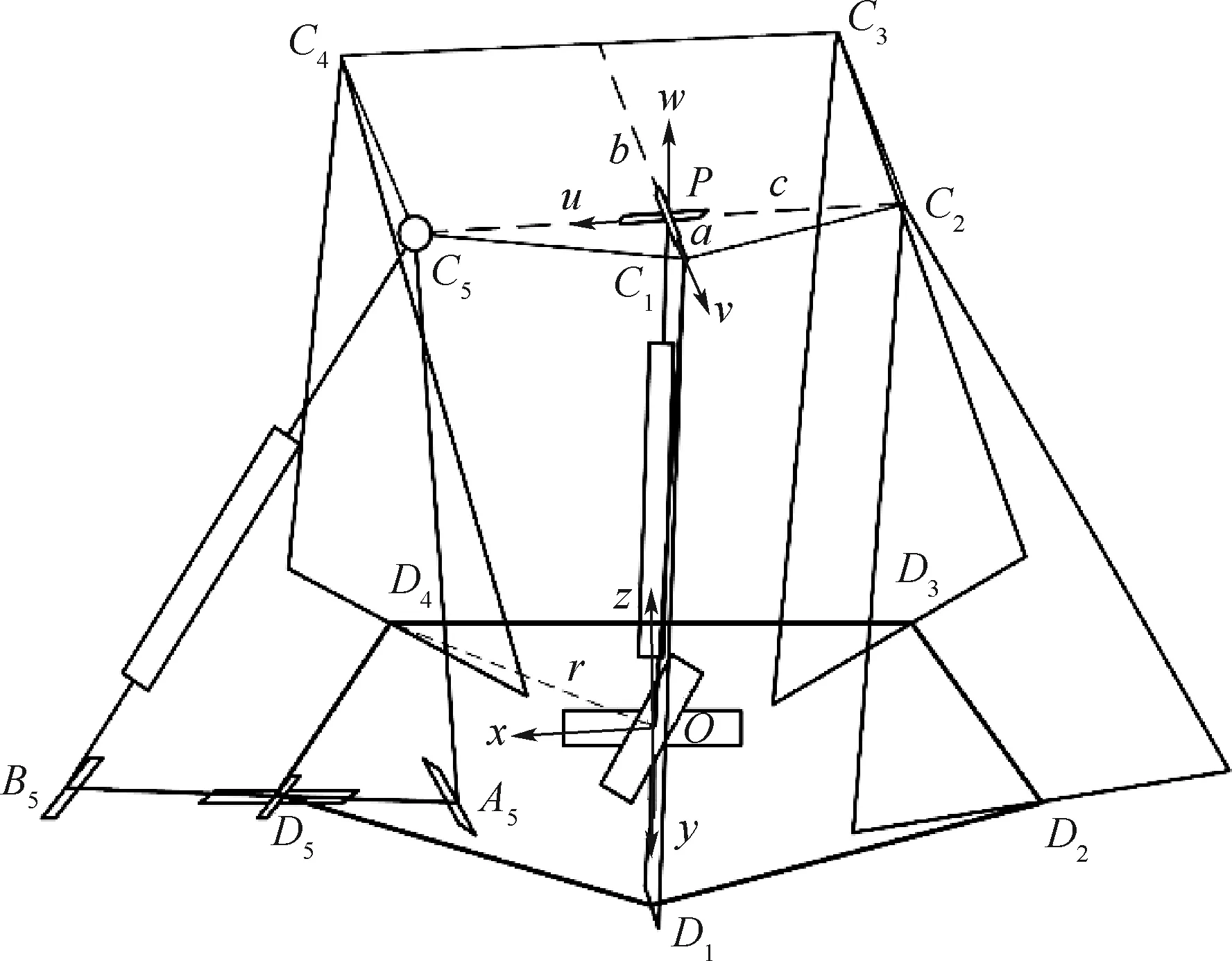
圖4 新型5-U(RRP)S/(8U)PU并聯機構結構簡圖Fig.4 Structure diagram of a new type of 5-U(RRP)S/(8U)PU parallel mechanism

2 自由度計算

新型5-U(RRP)S/(8U)PU并聯機構的主動支鏈和被動支鏈的結構形式不同，因此自由度計算需要分別考慮2種支鏈。

對于被動支鏈(8U)PU， U副的軸線分別沿x和y方向；8U結構的自由度數目為2，具體為沿x和y方向的移動，但這2個移動耦合了沿z方向的移動。因此，當8U機構和軸線沿z方向的P副連接時，可等效看作空間內沿x、y和z方向的3個P副，那么原(8U)PU支鏈在運動學上可等效為UPPP支鏈。對于該支鏈，易得到其自由度數目為5，分別為沿x、y、z方向的移動和繞x、y方向的轉動。

對于主動支鏈U(RRP)S，由于5條支鏈結構相同，故取支鏈1進行分析。圖5為支鏈1的結構簡圖。支鏈1在初始位姿時位于定系yOz平面內，現以點D為原點建立坐標系Dxyz，并對各運動副進行如圖5所示的編號。設支鏈1中各個參數如下：AD=DB=l1/2,AC=l2,BC=l3，桿AB初始仰角為γ；在一般位置時，虎克鉸D轉過的角度分別為θ1和θ2，桿AB與桿BC夾角為θ3。利用螺旋理論[18]可以分別求得各運動副的運動螺旋如下：

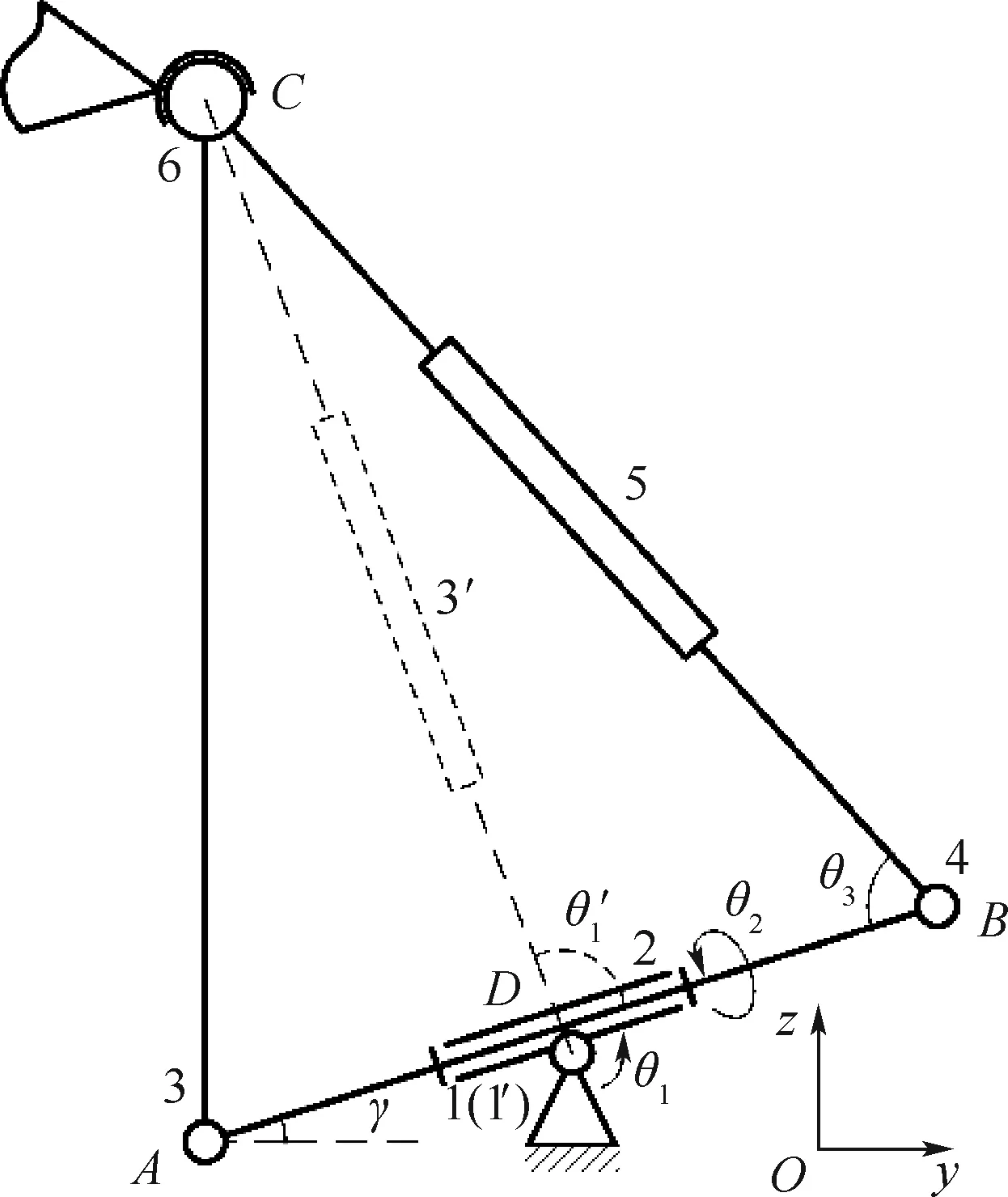
圖5 支鏈1結構簡圖Fig.5 Structure diagram of limb 1

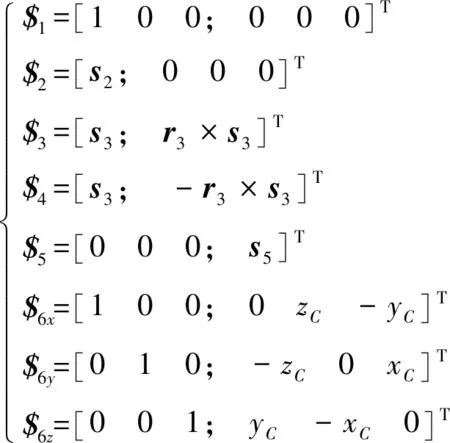
(1)

式中:

s2=[0 cos(θ1+γ) sin(θ1+γ)]

s3=[cosθ2sin(θ1+γ)sinθ2-cos(θ1+γ)sinθ2]

r3×s3=

xC=l3cosθ3sinθ2

l3cosθ3cosθ2sin(θ1+γ)

l3cosθ3cosθ2cos(θ1+γ)

將式(1)組合后即可得到支鏈1的運動螺旋系為

$0=($1$2$3$4$5$6x$6y$6z)

(2)

綜上所述，由于每條主動支鏈的自由度為6，對動平臺不提供約束，所以動平臺和中間被動支鏈具有相同的自由度數，即沿x、y、z方向的移動和繞x、y方向的轉動。

3 運動學分析

3.1 位置反解

已知動平臺的位姿，以初始位姿為基準，可給出動平臺在某一時刻的位姿參數如下：(x,y,z)為動系原點P沿x、y、z軸移動的距離；α為動平臺繞u軸轉過的角度；β為動平臺繞v軸轉過的角度。現求解驅動P副的位置即求解桿BiCi的長度。

由圖4可建立第i(i=1,2,…,5)條支鏈的封閉矢量方程為

(3)

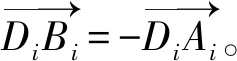
(4)

首先，利用坐標變換可得Ci在定系的坐標為

(5)

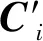
然后，求出Di在定系的坐標為

(6)

(7)

式中:θ1,i為未知量，表征第i條支鏈繞U副一條轉動軸線的轉角。

將式(5)～式(7)代入式(4)，由于AiCi為固定桿長l2，BiCi為所需求的位置l3,i，利用桿長條件可得方程組，未知量為θ1,i、l3,i，即可解得l3,i。

3.2 位置正解

已知各驅動P副的位置，即桿BiCi的長度l3,i，現求解動平臺的位姿參數(x,y,z,α,β)。

當桿BiCi的長度已知時，三角形AiBiCi各邊長確定，為固定桁架結構，可等效看作固定桿CiDi，利用三角形中線定理可求得

(8)

寫成坐標點的形式為

(9)

將式(5)和式(6)代入式(9)中，其中未知量為(x,y,z,α,β)，共可得到5個方程，則可唯一求解出動平臺的位姿。

3.3 求解雅可比矩陣

采用螺旋理論進行雅可比矩陣的求解[19]。共分為2個部分：約束雅可比矩陣和運動雅可比矩陣。各運動副的運動螺旋表示如圖6所示，圖中sj,i表示第i支鏈的第j個運動副的軸線方向。

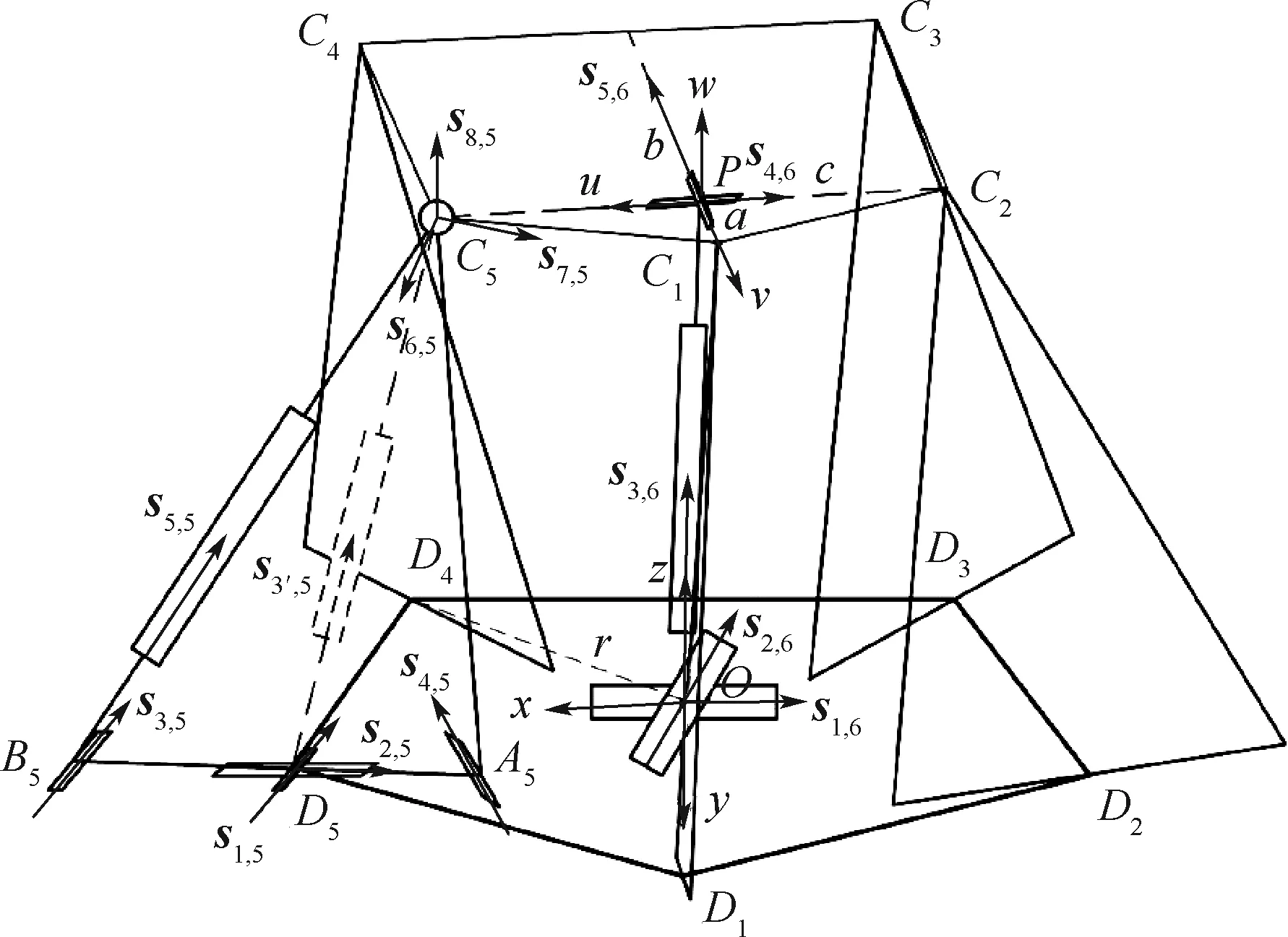
圖6 各運動副的運動螺旋Fig.6 Twist of each kinematic pair

首先，求解約束雅可比矩陣。由于主動支鏈對動平臺不提供約束，因此僅考慮被動支鏈。由第2節可知，(8U)PU支鏈可等效為UPPP支鏈，易得到其自由度分別為沿x、y、z方向的移動和繞x、y方向的轉動。動平臺的瞬時速度$P可表示為

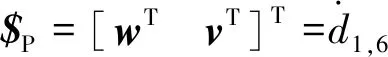
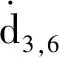
(10)

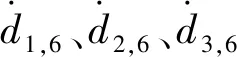
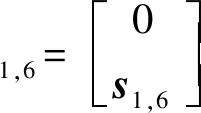
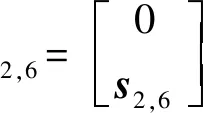
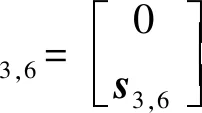
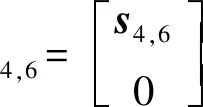
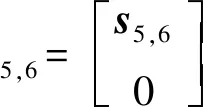
求得其反螺旋為

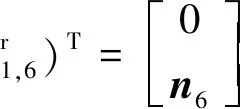
(11)

式中:n6為s4,6和s5,6公垂線方向。

將式(10)與式(11)做互易積并整理得

JC$P=0

(12)

式中:JC為該機構的約束雅可比矩陣，即

(13)

其次，求解運動雅可比矩陣。由于被動支鏈不存在驅動副，因此僅考慮主動支鏈。對于主動支鏈，支鏈本身為閉環結構，需等效為開環結構才可用螺旋理論進行求解雅可比矩陣。根據第2節的自由度計算和支鏈的運動形式不難發現，閉環四桿機構AiBiCi的運動可等效成如圖5所示的P副3′、R副1′，其中1′與U副的轉動軸線1共軸。

將式(8)對時間t求導得

(14)

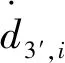
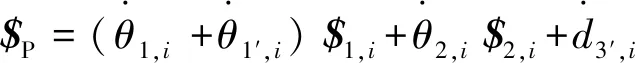
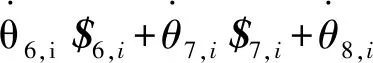
(15)

將驅動P副剛化，驅動支鏈為US結構，因此該支鏈會產生一個額外的反螺旋為

(16)

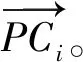
將式(15)與式(16)做互易積得

(17)

將式(14)代入式(17)整理，將5條支鏈疊加后得

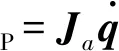
(18)

式中:

綜上所述，將式(13)與式(18)疊加即可得機構的完整雅可比矩陣為

(19)

4 工作性能分析

4.1 定姿態工作空間

4.1.1 理論分析

在實際工程應用中，對于新型5-U(RRP)S/(8U)PU并聯機構動平臺的調姿轉角要求很小，因此僅分析該機構的定姿態工作空間。

該機構的主動支鏈和被動支鏈的運動具有解耦特性，整個機構的工作空間可看作是主動支鏈和被動支鏈獨立工作空間的公共重合區域，因此需分別計算2個獨立定姿態工作空間。

對于被動支鏈，影響工作空間的主要因素有P副的移動距離和8U結構中U副的轉角限制。

設每個U副轉角為θ6，其約束條件可表示為

-θ6m≤θ6≤θ6m

(20)

設P副的移動距離為l6，其約束條件可表示為

l6min≤l6≤l6max

(21)

如圖7所示，8U結構點O′處的工作空間是以O為原點、d為半徑的球冠面。

對于主動支鏈，影響工作空間的主要因素有P副的移動距離及復合S副處桿AiCi和桿BiCi的相對轉角限制。

設P副的移動距離為l3,i，其約束條件可表示為

l3,imin≤l3,i≤l3,imax

(22)

設桿AiCi和桿BiCi的相對轉角為θi，其約束條件可表示為

θimin≤θi≤θimax

(23)

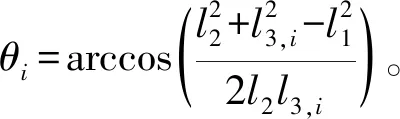
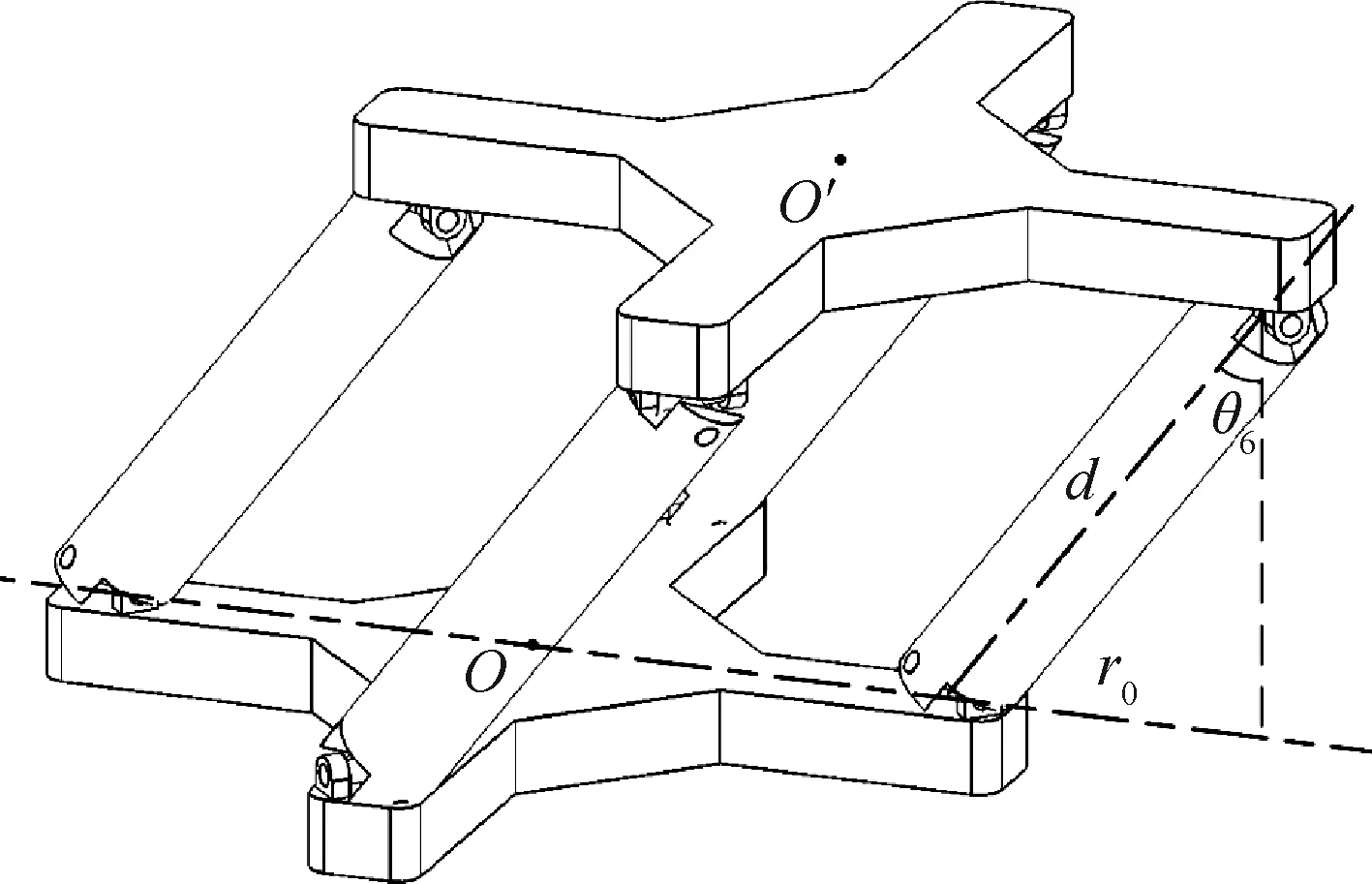
圖7 8U結構工作空間示意圖Fig.7 Schematic diagram of workspace of 8U structure

4.1.2 計算實例

對該機構的尺寸參數及約束范圍進行賦值后整理如表1所示。

設初始位置時z=300 mm，在不考慮桿件干涉的情況下，根據表1可分別繪制出z≥0時主動支鏈和被動支鏈的定姿態工作空間，如圖8和圖9所示，將2個工作空間取交集后得到機構的工作空間如圖10所示。

由此可見，在尺寸約束等條件下，該機構的定姿態工作空間由8U結構的轉角范圍(即被動支鏈工作空間的粗細)和三角形結構的最大、最小伸縮量(即主動支鏈工作空間類球殼體的厚度)決定。

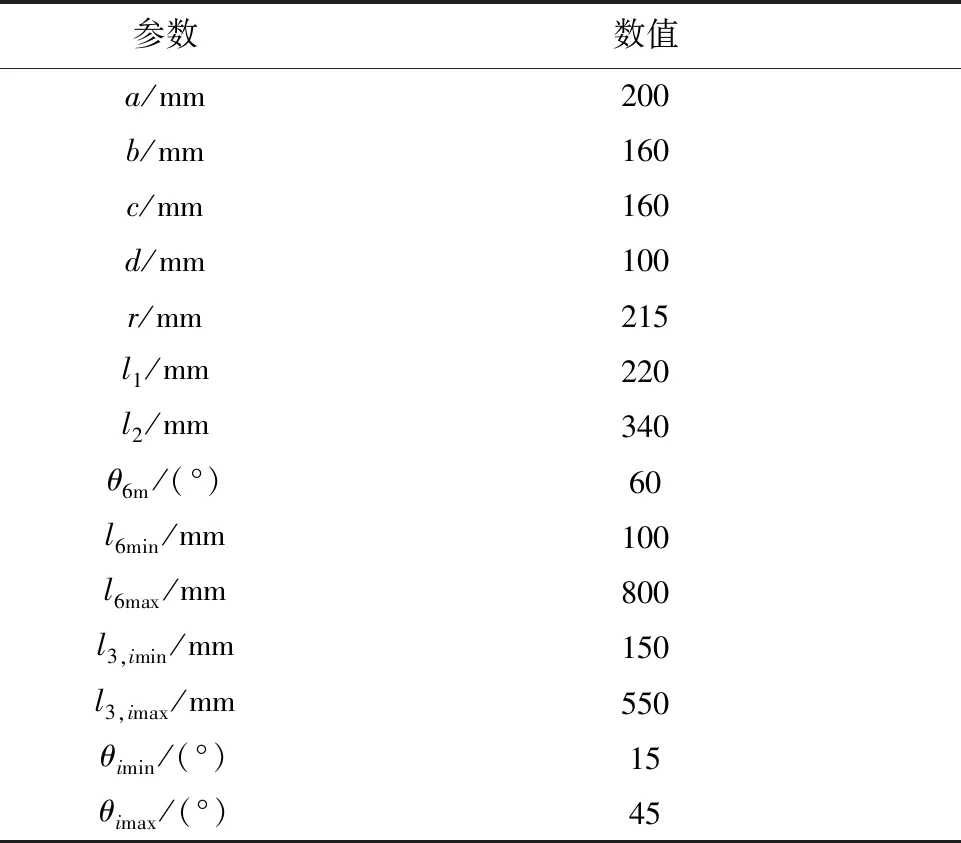
表1 并聯機構尺寸參數Table 1 Dimension parameters of parallel mechanism

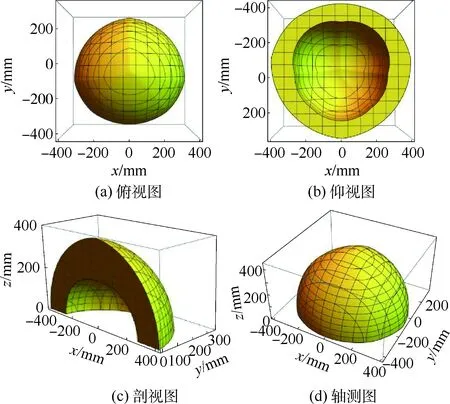
圖8 主動支鏈工作空間Fig.8 Workspace of active limb

4.2 靜剛度分析

機構在運動過程中剛度隨位姿參數的變化而產生的變化趨勢是衡量該機構是否具有高剛度的一個重要指標。

根據文獻[20]，靜剛度矩陣為

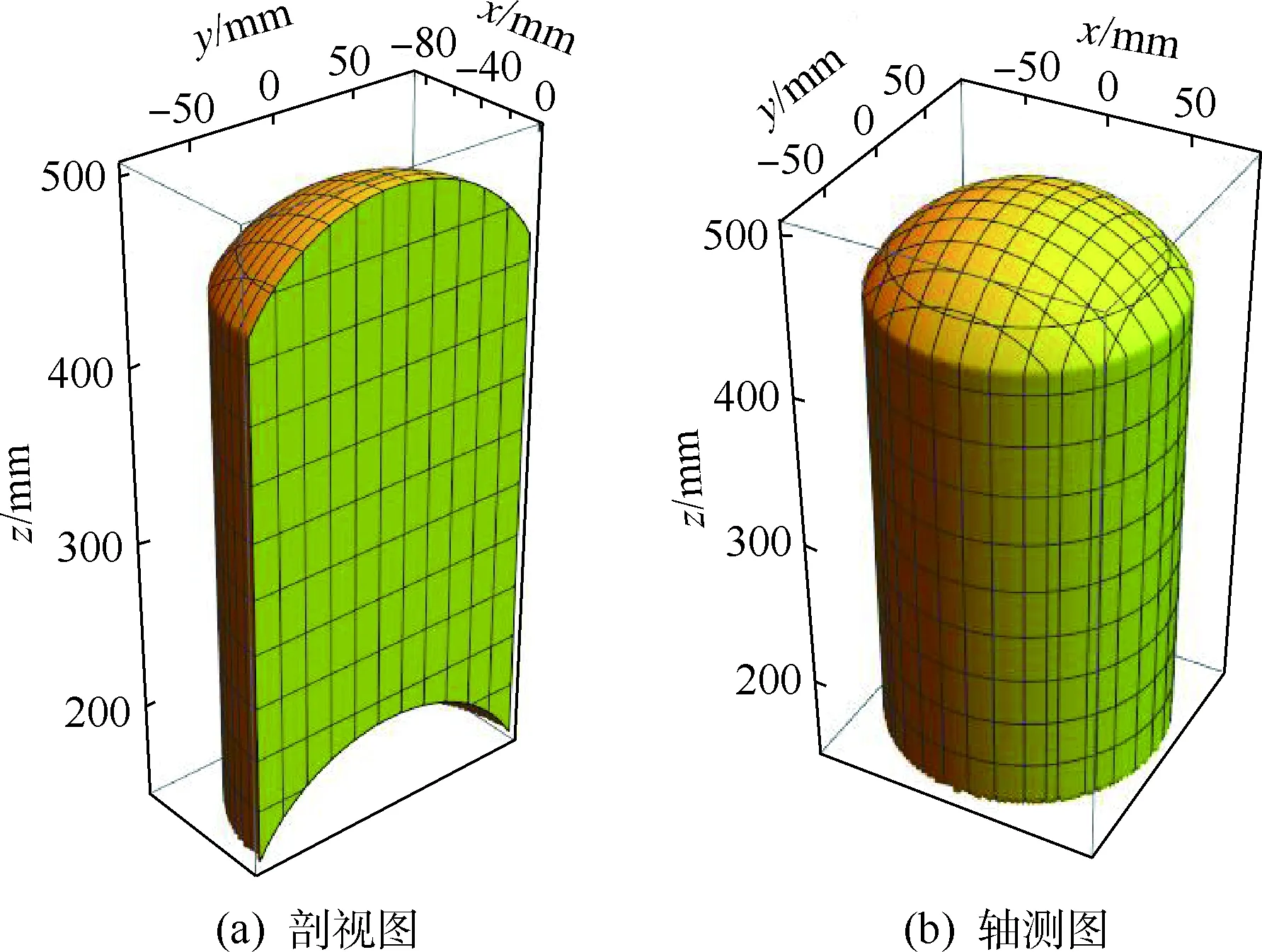
圖9 被動支鏈工作空間Fig.9 Workspace of passive limb

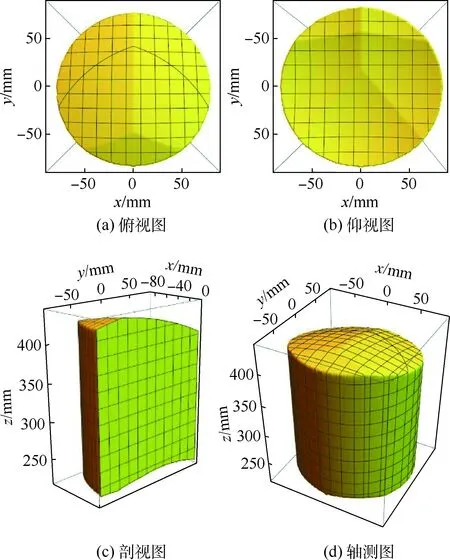
圖10 整體機構工作空間Fig.10 Workspace of whole mechanism

K=kJTJ

(24)

式中:k為各關節的等效彈簧系數；J為機構的雅可比矩陣。

動平臺的等效力螺旋F與其微小變形量Δx的關系為

F=KΔx

(25)

現選用將靜剛度矩陣K的最小特征值λmin作為評價靜剛度性能的指標。

當機構動平臺位置固定，即x=0,y=0，z=300 mm時，動平臺的剛度隨其轉角α、β的分布如圖11所示。

當機構動平臺姿態固定，即α=0，β=0時，動平臺的剛度隨其位移x、y、z的分布如圖12所示。

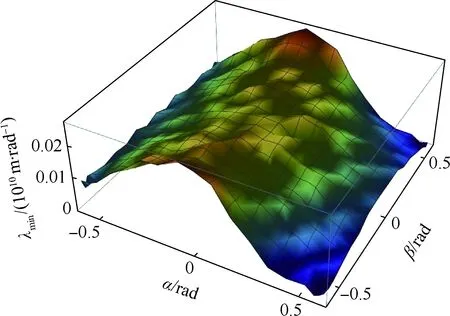
圖11 定位置下剛度隨轉角的分布Fig.11 Distribution of stiffness with rotation angle under fixed position

從圖11中可以看出，當α一定時，剛度隨β絕對值的增大或增或減，但變化不明顯；當β一定時，剛度隨α絕對值的增大而減小。

從圖12中可以看出，剛度隨x絕對值的增大而減少，隨y絕對值的增大變化不明顯，隨z的增大而增大。

5 對比與仿真

為驗證新型5-U(RRP)S/(8U)PU并聯機構的可行性以及其主動支鏈的結構形式相對于一般機構是否具有優勢，現選擇與之相似的5-UPS/(8U)PU機構(見圖13)與之進行對比。

5-UPS/(8U)PU機構由5條主動支鏈和1條被動支鏈構成，其主動支鏈為常見的UPS結構，被動支鏈則選擇與新機構相同的(8U)PU結構，以減少其他因素對結果的影響。趙永生等[21]對5-UPS/PRPU機構進行了運動學分析等研究，該機構與5-UPS/(8U)PU機構類似，由于被動支鏈上不含有驅動副，對機構的運動學特性影響較小，因此其運動學分析方法可用于5-UPS/(8U)PU機構，此處不再贅述，并最終得出5-UPS/(8U)PU機構可控性好的特點。

對于新型5-U(RRP)S /(8U)PU機構，從圖6中不難看出，式(8)中的等效桿CiDi即為5-UPS/(8U)PU機構的主動支鏈，因此CiDi的長度可看作5-UPS/(8U)PU機構中移動驅動副的變化量，設新機構的驅動副的變化量為L，對比機構的驅動副的變化量為LC，由式(8)可得兩者關系為

(26)

式中:K為常數。

由此可見，L與LC滿足雙曲函數關系，當兩 者都大于0時，L隨LC單調遞增。結合式(14)，新機構中驅動副速度與對比機構中驅動副速度呈線性關系。

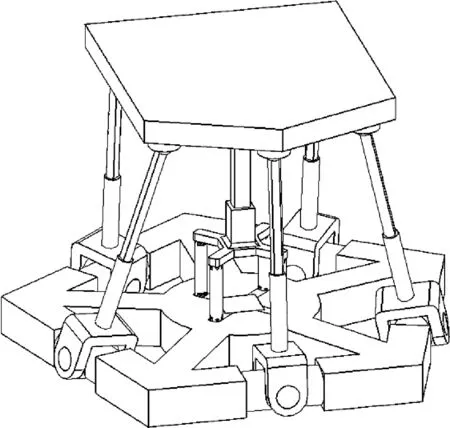
圖13 5-UPS/(8U)PU并聯機構結構示意圖Fig.13 Schematic of 5-UPS/(8U)PU parallel mechanism

因此，當5-UPS/(8U)PU機構具有良好的可控性時，新型5-U(RRP)S/(8U)PU機構也具有較好的可控性。

接下來驗證新型5-U(RRP)S/(8U)PU機構是否具有更高的精度和剛度。利用ADMAS軟件對該機構和對比機構進行仿真。

用于對比的機構結構除了主動支鏈采用UPS結構外，機構的尺寸參數、結構布局和初始位姿等都與本文機構相同，以此減少除構型以外的因素產生的誤差。

首先驗證本文機構的精度。將2種機構的動平臺運動進行軌跡規劃，為保證對比的準確性，動平臺的運動應盡可能簡單，現規劃2種機構的動平臺運動為從初始位姿沿z軸方向移動100 mm，通過仿真后得到的2種機構各驅動P副的位移數據如表2所示，整理后如圖14所示。

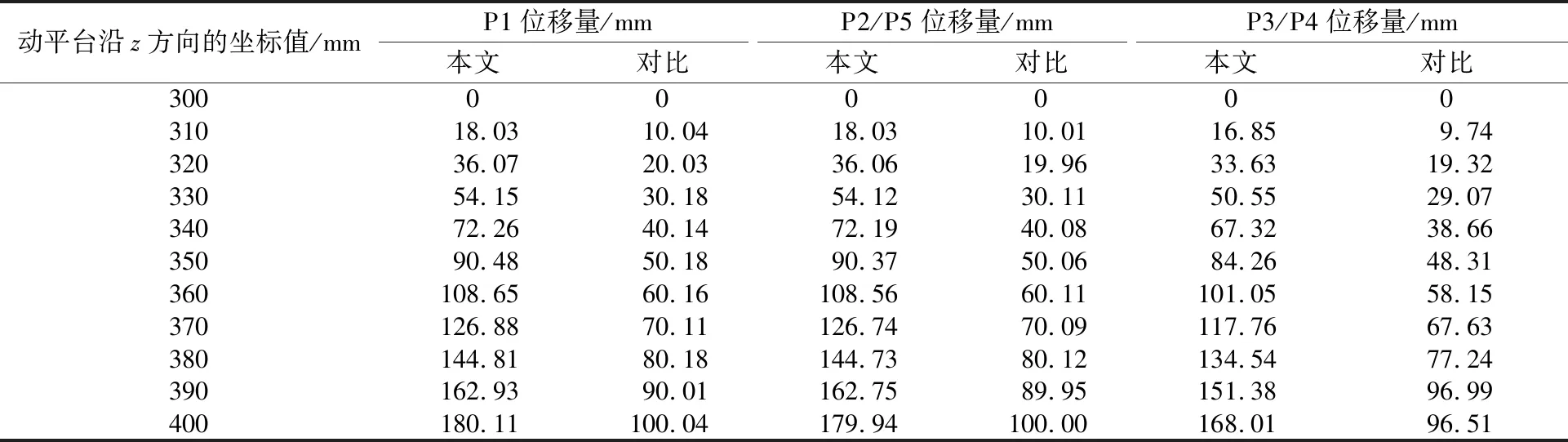
表2 各支鏈驅動副位移量Table 2 Displacement of driving joint on each limb

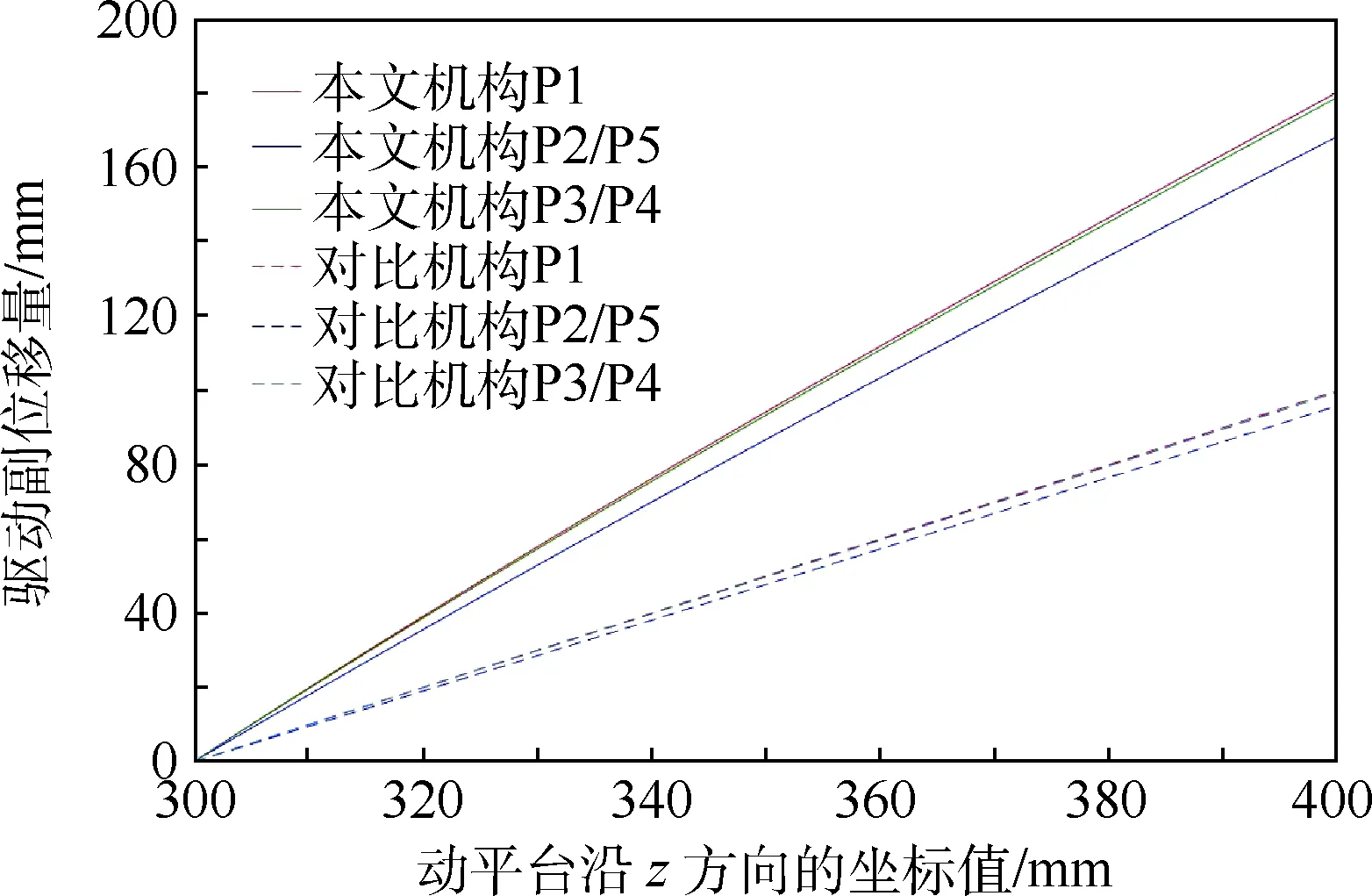
圖14 驅動副位移量變化曲線Fig.14 Changing curves of driving joints’ displacement

從圖14中可以看出，當動平臺進行相同運動時，本文機構驅動副的位移量相比于一般機構要增加近100%。因此，本文機構通過增加驅動副的變化量使得驅動電機對動平臺的控制精度提高了近1倍。

其次，驗證本文機構的剛度。當動平臺受到外界的阻力時，各驅動副所承受力的大小可以作為評價機構剛度的標準。現設定2種機構各個驅動副的運動速度相同，具體數值如表3所示。

給2種機構的動平臺施加相同的外界壓力，大小為800 N，方向始終沿重力方向。在保持上述速度下2種機構的驅動電機同時運行5 s，通過仿真后得到2種機構各驅動P副的受力大小，如表4所示，整理后如圖15所示。

表3 各支鏈驅動副電機運行速度Table 3 Motor operation speed of drivingjoint on each limb

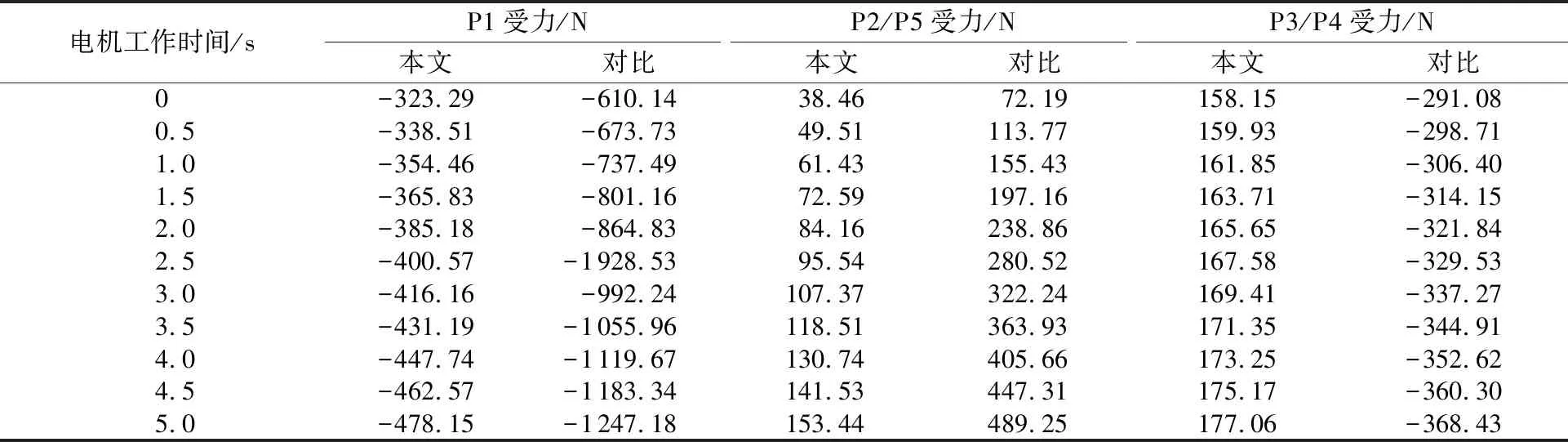
表4 各支鏈驅動副受力Table 4 Force of driving joint on each limb

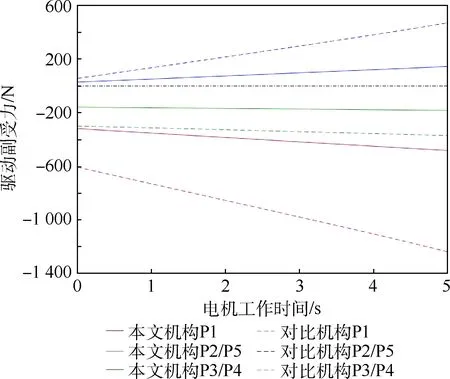
圖15 驅動副受力變化曲線Fig.15 Changing curves of driving joints under force

從圖15中可以看出，當動平臺受力相同且驅動副運動相同時，本文機構驅動副的受力約為一般機構的1/3。因此，本文機構使得驅動副的結構剛度提高了近2倍。

6 結 論

為解決導彈殼體的自動套裝要求，本文提出了一種用于位姿調整的新型5-U(RRP)S/(8U)PU并聯機構。采用被動支鏈進行約束，同時主動支鏈采用三角形閉環結構，以提高機構的精度、剛度和穩定性。

1) 進行了自由度計算及運動學分析，利用位置關系分別繪制了主動支鏈與被動支鏈的工作空間并綜合，利用全雅可比矩陣建立了剛度模型。

2) 選取主動支鏈為UPS支鏈的機構作為對比機構，利用ADAMS軟件同時對2種機構進行仿真，一方面驗證了機構運動的可行性，另一方面通過軟件仿真初步得出本文機構相比于對比機構的精度提高了近1倍，剛度提高了近2倍。