一題多向探究 高效提升能力

許銀伙

(福建省泉州外國語中學 362000)

一、例題

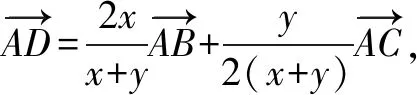
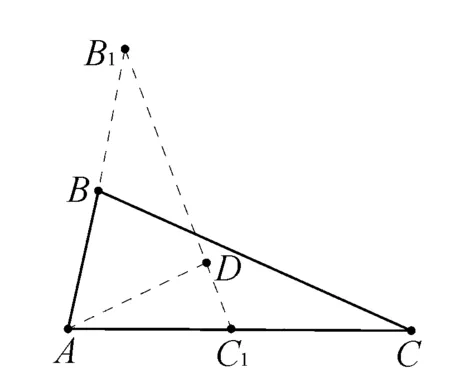
圖1

二、解法與分析

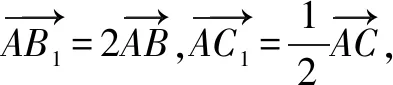
由已知得：△ABC?△AB1C1，∴B1C1=6，AB1=2AC1，設AC1=b，則AB1=2b.

分析一求△AB1C1邊B1C1的高h的問題，可以聯系△AB1C1的面積公式，因此引入兩邊的夾角作為函數的變量，探求高h與引入變量的函數式，利用函數知識解決.

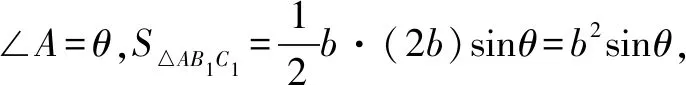
評注1. 針對12sinθ+4hcosθ=5h，引入輔助角利用化一公式，即逆用兩角和或差的正余弦函數公式解決，是求三角函數最值的常用方法.2.求最值一定要驗證最值可以取得.3.本題解答也可以利用△ABC?△AB1C1化為求△ABC邊BC的高.

分析二方法一針對12sinθ+4hcosθ=5h，考慮到 cos2θ+sin2θ=1，也可以通過換元，轉化成直線與圓的位置關系來解決.

方法二(接方法一)令u=cosθ，v=sinθ，得u2+v2=1且12v+4hu=5h，

評注1.換元后應注意新變量的取值范圍，利用不等式獲得最值必須驗證取等號.

2.轉化為幾何問題，應充分利用幾何性質，以簡化運算.

分析三針對12sinθ+4hcosθ=5h，還可以考慮運用三角函數的萬能公式進行換元，把三角函數問題轉化成代數問題解決.

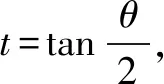
評注本方法通過換元，化三角問題為代數的函數問題，利用基本不等式解決.

分析四針對分式函數，分子分母最高次數是兩次的整式，除了利用基本不等式求最值，還可以轉化成一元二次方程有解的條件解決.

評注利用一元二次方程的判別式大于或等于0求最值或值域是常用方法，不可忽略.

分析五在實際問題中，所得變量往往需要限制范圍，把方程解的范圍先納入解答的思考中，即可獲得更加有深度的解答.

評注本方法與上一種方法類似，只是研究得更深入一些，思維層次更高一些，關注到方程解的范圍，在利用方程求參數范圍時一定要這樣思考.

分析六導數是解決函數最值的常用工具，運用導數可以很方便獲得函數的單調區間，從而求出極值和最值.

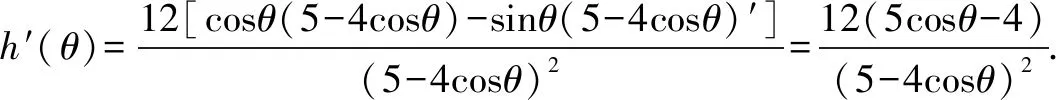
評注本方法由導數推得函數的單調性，是比較容易想到的思路，但運算量較大，且需要用到三角函數的單調性，還是有一定難度的.

分析七建立適當的直角坐標系，通過幾何條件，可以獲得動點的軌跡情況，從而直觀地求出最值.

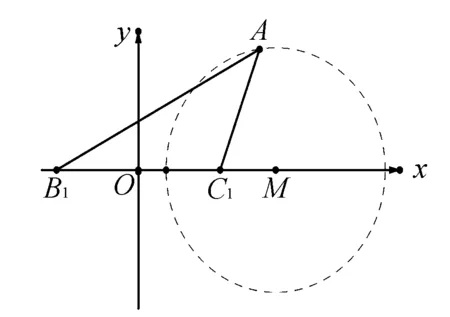
圖2

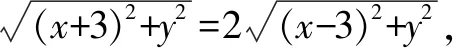
化簡得：(x-5)2+y2=16，所以點A在以點M(5,0)為圓心，4為半徑的圓上(去除與x軸的交點).因為圓心M(5,0)在直線B1C1上，所以點A到直線B1C1距離最大值是圓的半徑4，即得所求最大值為4.

評注由動點到兩個定點的距離之比是不等于1的非零常數，其軌跡是阿波羅尼斯圓，通過建立坐標系，利用圓的性質可以快速且直觀地解決問題.

數學知識并不是孤立存在，它們相互聯系，相互促進，因此數學問題的解決可以從不同的角度，用不同的知識加以分析，加以探究，從而尋找出精彩各異解決方法.但因為對已知條件和問題本質的把握深度不同，解答的簡繁程度也會有較大差異，經常對問題進行多方探究，無疑是自我磨練，提高數學能力的秘訣.

同類練習

1.(2018廈門第二次質檢)等邊△ABC邊長為1，點P在其外接圓劣弧AB上，則S△PAB+S△PBC的最大值為____.

2．(2018福建省備考指導適應性3)△ABC中，D為BC邊上的點，滿足AB=2AC，BD=2DC,△ABD的面積為2，則BC的最小值是____