淺談《線性代數(shù)》中的實(shí)例教學(xué)

徐清華 趙清波 劉 爍 吳克堅(jiān) 梁銳華

(空軍軍醫(yī)大學(xué)基礎(chǔ)醫(yī)學(xué)院數(shù)理教研室 西安 710032)

線性代數(shù)是我校針對(duì)生物醫(yī)學(xué)工程專業(yè)開設(shè)的一門重要基礎(chǔ)課，它在很多學(xué)科比如計(jì)算機(jī)科學(xué)，生物學(xué)，通信，航空等領(lǐng)域中都有廣泛的應(yīng)用。生物醫(yī)學(xué)工程專業(yè)是一門綜合理學(xué)、醫(yī)學(xué)和工學(xué)的交叉學(xué)科，因此線性代數(shù)在醫(yī)工專業(yè)的后續(xù)課程，如電路，信號(hào)與系統(tǒng)，數(shù)字信號(hào)處理等課程中都有重要應(yīng)用。

但是線性代數(shù)內(nèi)容抽象，邏輯性強(qiáng)，很多學(xué)生并未體會(huì)到這門課程的價(jià)值和趣味所在，因此如何讓學(xué)生了解這門課程在后續(xù)課程中的重要作用，從而提高學(xué)生的學(xué)習(xí)興趣，是我們一直關(guān)注的一個(gè)問題。在多年的教學(xué)實(shí)踐中，我們通過不斷探索發(fā)現(xiàn)，只有結(jié)合實(shí)例的教學(xué)，才能讓抽象的理論變得形象生動(dòng)，才能激發(fā)學(xué)生的學(xué)習(xí)興趣。因此，本文就實(shí)際教學(xué)過程中使用的一些案例做一些簡(jiǎn)單介紹。

1 向量組的線性相關(guān)性及藥方配制問題

向量組的線性相關(guān)性是線性代數(shù)中最重要的內(nèi)容，它是后續(xù)求解線性方程組的基礎(chǔ)，更是矩陣的秩和方程組解的結(jié)構(gòu)連接的紐帶。這一節(jié)的內(nèi)容理論性非常強(qiáng)，比如向量組的線性相關(guān)性的概念、最大線性無關(guān)組的定義、向量的線性表示等內(nèi)容，撲面而來的大量定義、定理和術(shù)語，讓學(xué)生感到非常困惑，無法理解，更不能在實(shí)際應(yīng)用中靈活應(yīng)用。

因此，如果在理論之后適當(dāng)增加實(shí)例的教學(xué)，能減輕學(xué)生對(duì)理論知識(shí)的畏懼感，激發(fā)學(xué)生的學(xué)習(xí)興趣，促進(jìn)學(xué)生主動(dòng)思考，培養(yǎng)學(xué)生理論聯(lián)系實(shí)際的能力。因此結(jié)合學(xué)生專業(yè)特點(diǎn)，我們引入了中成藥藥方配制問題，來幫助學(xué)生理解向量組的線性相關(guān)性和向量的線性表示等知識(shí)。

中成藥藥方配制問題：某醫(yī)院藥劑科用九種中草藥(A-I)，根據(jù)適當(dāng)?shù)谋壤渲瞥闪?種特效藥，各用量成份見表1。

表1 7種特效藥用量成份表(單位:g)

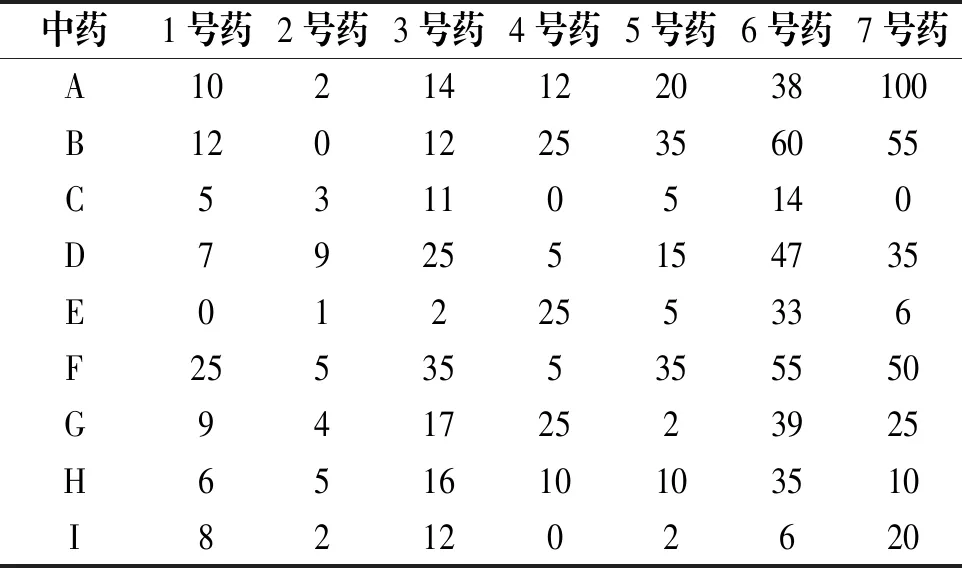
中藥1號(hào)藥2號(hào)藥3號(hào)藥4號(hào)藥5號(hào)藥6號(hào)藥7號(hào)藥A10214122038100B1201225356055C531105140D79255154735E012255336F255355355550G94172523925H651610103510I821202620

(1)某藥店要購(gòu)買這7種特效藥，但藥劑科的第3號(hào)藥和第6號(hào)藥已經(jīng)賣完，請(qǐng)問能否用其它特效藥配制出這兩種脫銷的藥品？

(2)現(xiàn)在藥劑科想用這7種特效藥配制3種新藥，表2給出了3種新藥的成份比例，請(qǐng)問是否能配制？如何配制？

表2 3種新藥的成份比例

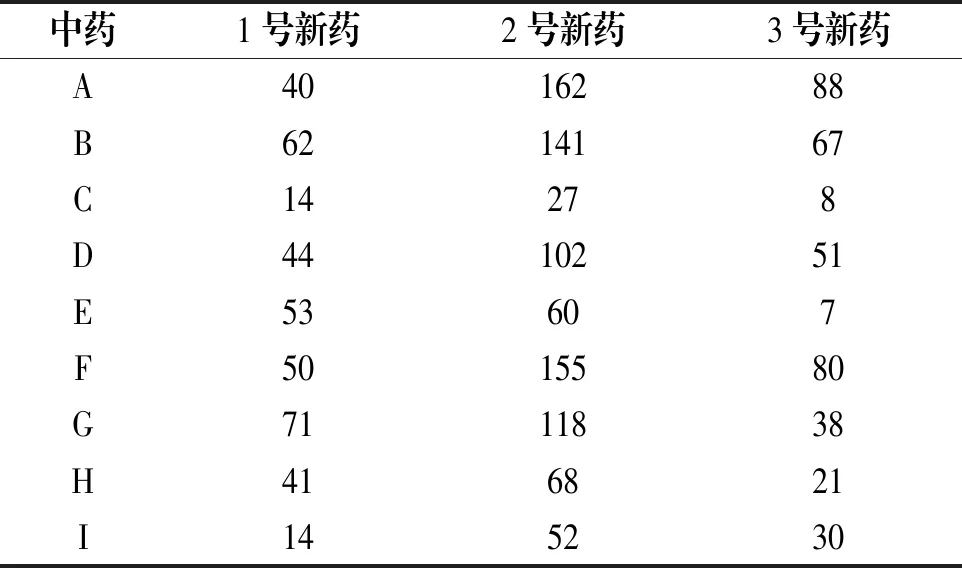
中藥1號(hào)新藥2號(hào)新藥3號(hào)新藥A4016288B6214167C14278D4410251E53607F5015580G7111838H416821I145230

(1)這類題目同學(xué)們首次接觸比較困惑，但是仔細(xì)分析之后發(fā)現(xiàn)，如果把每一種特效藥看成一個(gè)九維列向量，那么能否用其它特效藥配制出第3號(hào)藥和第6號(hào)藥的問題，其實(shí)就是3號(hào)和6號(hào)這兩個(gè)向量能否用其余向量線性表示的問題，所以問題轉(zhuǎn)化為判斷7個(gè)向量構(gòu)成的向量組的線性相關(guān)性問題。如果向量組線性無關(guān)，那么無法配制需要的特效藥; 如果向量組線性相關(guān)，并且能找到一個(gè)最大線性無關(guān)組，u3,u6能被這個(gè)最大無關(guān)組線性表示，則可以配制3號(hào)和6號(hào)藥品。

由于數(shù)據(jù)量較大，若采用手工初等行變換計(jì)算較為麻煩，因此可采用數(shù)學(xué)軟件Matlab進(jìn)行計(jì)算，結(jié)果為：向量組線性相關(guān)，并且一個(gè)最大無關(guān)組為u1,u2,u4,u5,u7且u3=u1+2u2，u6=3u2+u4+u5，因此可以配置出這兩種脫銷的藥品。

(2)有了第一問的基礎(chǔ)， 第二問就比較簡(jiǎn)單了。3種新藥用v1,v2,v3來表示，能否配制新的特效藥的問題就轉(zhuǎn)化為v1,v2,v3能否由7個(gè)向量u1,u2,u3,u4,u5,u6,u7線性表示的問題，若能表示，則可配制；否則，不能配制。

用Matlab計(jì)算可得：v1=u1+3u2+2u4，v2=3u1+4u2+2u4+u7，v3則不能被線性表示，所以可以配制1號(hào)和2號(hào)新藥，3號(hào)新藥則無法配制。

2 方程組求解及電路問題

在線性代數(shù)的教學(xué)中，方程組的求解貫穿始終，利用行列式計(jì)算的克拉默法則，利用初等變換計(jì)算的通解，利用基礎(chǔ)解析寫出的通解，對(duì)這些求解方程組的方法，很多同學(xué)都很容易掌握，拿到題目都能熟練的計(jì)算，但是一遇到實(shí)際問題就束手無策，原因就是理論聯(lián)系實(shí)際能力太弱。

線性方程組應(yīng)用非常廣泛，很多實(shí)際問題的處理最后都?xì)w結(jié)為線性方程組的問題，比如在生物醫(yī)學(xué)工程專業(yè)的后續(xù)課程中，大部分電路的問題都可以轉(zhuǎn)化為方程組的問題來求解。

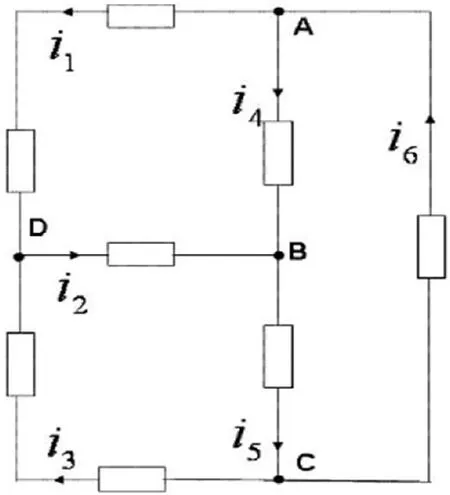
上圖為電路網(wǎng)絡(luò)圖，設(shè)各節(jié)點(diǎn)的電流如圖所示，要求出電路中各支路上的電流。由基爾霍夫第一定律可以列出方程：

對(duì)于節(jié)點(diǎn)A：i1+i4-i6=0;

對(duì)于節(jié)點(diǎn)B：i2+i4-i5=0;

對(duì)于節(jié)點(diǎn)C：i3+i6-i5=0;

對(duì)于節(jié)點(diǎn)D：i1+i3-i2=0;

于是求各個(gè)支路的電流就歸結(jié)為下面齊次線性方程組的求解

解之，得其解為

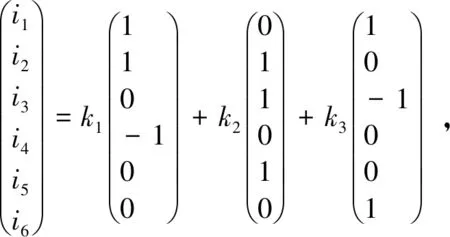
由于i1,i2,i3,i4,i5,i6均為正數(shù)，所以通解中的3個(gè)任意常數(shù)應(yīng)滿足以下條件：

k1<0,k2>k3>-k1

如果k1=-1,k2=3,k3=2，則：

i1=1,i2=2,i3=1,i4=1,i5=3,i6=2

3 矩陣的逆及加密通信問題

矩陣的逆在矩陣?yán)碚撝姓加蟹浅Ｖ匾牡匚唬彩且粋€(gè)較難理解的重點(diǎn)內(nèi)容。很多學(xué)生能熟練計(jì)算矩陣的逆，利用逆矩陣求解矩陣方程，但是卻不了解矩陣的逆在實(shí)際生活中的作用，對(duì)這部分的知識(shí)只停留在抽象的概念和機(jī)械的計(jì)算中。為了加深知識(shí)的應(yīng)用及知識(shí)點(diǎn)的深刻理解，我們選取了同學(xué)們比較感興趣的保密通信方面的一個(gè)問題來講解。

加密技術(shù)在通信中有著重要的作用，加密的原理如下：發(fā)送方采用某種算法，也就是密鑰，將明文數(shù)據(jù)加密轉(zhuǎn)化成密文數(shù)據(jù)后發(fā)送給接受方，接收方則可以采用對(duì)應(yīng)的某種算法將密文數(shù)據(jù)解密轉(zhuǎn)換成明文數(shù)據(jù)。從矩陣的角度來解釋就是，明文用矩陣X來表示，加密密鑰為矩陣A，則加密過程就是矩陣方程AX=C，密文是矩陣C，解密密鑰為矩陣B，解密的過程為X=BC，加密技術(shù)是否有效，關(guān)鍵在于能否還原成明文。

我們來分析一下這兩個(gè)矩陣方程，看這兩個(gè)密鑰矩陣A，B之間的關(guān)系。由于AX=C，X=BC，則有ABC=C，即AB=E，所以在保密通信中，密鑰只有一個(gè)，解密密鑰是通過這個(gè)關(guān)系式AB=E得到的，也就是加密密鑰和解密密鑰互為逆矩陣B=A-1。

比如，在2008年諜戰(zhàn)大片《潛伏》中，地下工作者余則成收到王翠平傳遞來的秘密消息，是20個(gè)數(shù)字，這個(gè)消息可以用一個(gè)4行5列的矩陣來表示

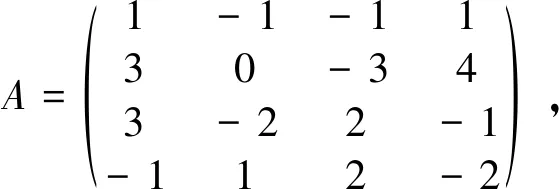
保密通信問題是當(dāng)今信息時(shí)代發(fā)展的一個(gè)重要研究課題，實(shí)際的加密模型相當(dāng)復(fù)雜，上面所舉的例子只是為了說明逆矩陣應(yīng)用的一個(gè)最簡(jiǎn)單的模型。

線性代數(shù)的應(yīng)用例子還有很多。比如在數(shù)字圖像處理中，簡(jiǎn)單的應(yīng)用有：圖像的變暗或變量可用矩陣的數(shù)乘來實(shí)現(xiàn)；圖像旋轉(zhuǎn)可用矩陣的轉(zhuǎn)置、矩陣的線性變換來實(shí)現(xiàn)；圖形復(fù)原可用矩陣的逆來實(shí)現(xiàn)；圖像的分割可用矩陣子塊的提取來實(shí)現(xiàn)等等。

線性代數(shù)的應(yīng)用非常廣泛，它是最有趣的一門數(shù)學(xué)課程，也是最有用的一個(gè)應(yīng)用工具，因此在實(shí)際教學(xué)中必須響應(yīng)其它學(xué)科的需求，從具體的、實(shí)際的例子出發(fā)來介紹概念、原理、理論的發(fā)展，這樣才能讓學(xué)生在后續(xù)課程的學(xué)習(xí)中體會(huì)到線性代數(shù)這門課程的重要作用。