巧解第35屆預賽中的拋體問題
李志雄
(莆田第十中學,福建 莆田 351146)
1 第35屆全國中學生物理競賽預賽中的拋體問題
第35屆預賽第6題:田徑場上某同學將一鉛球以初速度v0拋出,該鉛球拋出點的高度為H.鉛球在田徑場上的落點與鉛球拋出點的最大水平距離為________,對應的拋射角為________.重力加速度為g.
2 解法探討
這是一個與生活實際直接相關的經典問題,在許多物理競賽類的教輔書中都有此問題的解答,一般是以時間t為參數,從運動方程出發來計算,這種解法思路自然,但計算復雜.下面利用中學數學技巧給出2種簡捷的解法,從中能使人體驗到數理結合的科學美.
2.1 利用柯西不等式
(1) 柯西不等式簡介.
柯西不等式是目前高中數學選修4-5中的內容,但不如均值不等式一樣為物理教師所熟悉,下面先從平面向量的背景介紹二維形式的柯西不等式.
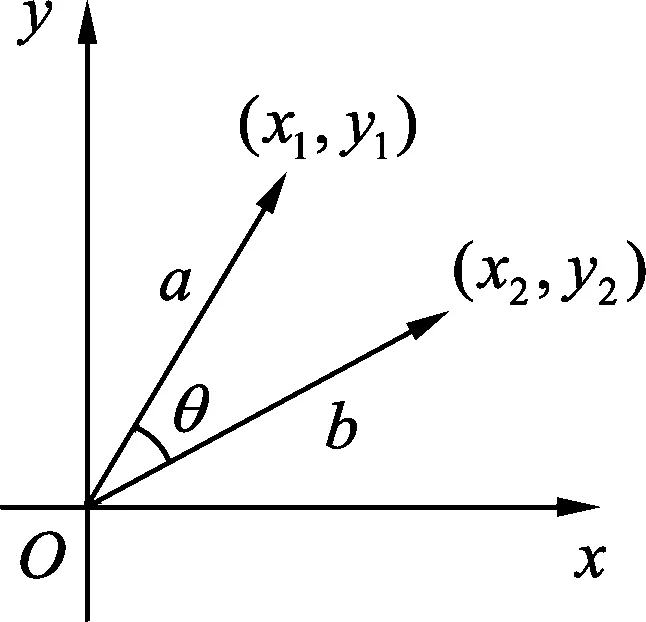
圖1
如圖1所示,設在平面直角坐標系中有向量a=(x1,y1),b=(x2,y2),a與b之間的夾角θ,根據向量數量積的定義有
a·b=|a||b|cosθ.
(1)
因|cosθ|≤1,所以有
|a·b|≤|a||b|.
(2)
用平面向量坐標表示(2)式,得
(3)

(2) 分析與解答.
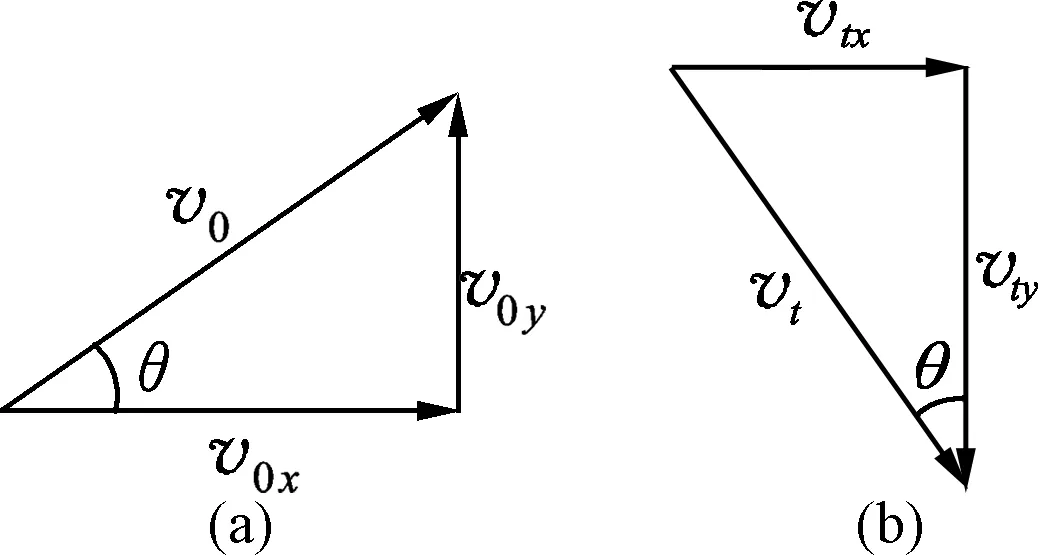
圖2
(1)
落點與鉛球拋出點水平距離為
x=v0xt.
(2)
由(1)、(2)式得
(3)
注意到v0x=vtx,將(3)式變形,利用柯西不等式有
即落點與鉛球拋出點的最大水平距離為
根據柯西不等式取極值時的條件,拋得最遠時有
則圖2(a)和圖2(b)中2個速度矢量三角形相似,設此時拋射角為θ,有
2.2 利用矢量三角形

圖3
如圖3所示,初速度v0、落地時末速度vt、速度改變量Δv構成矢量三角形OAB,設拋射角為θ,末速度vt方向與水平線夾角為α,注意到Δv大小為gt,矢量三角形面積為
(1)
落點與鉛球拋出點水平距離為
x=v0cosθ·t.
(2)
由(1)、(2)式可得
(3)
由(3)式知,只要使三角形OAB的面積S最大,水平射程x就能達到最遠,而此矢量三角形的
面積也可用正弦公式表示為
(4)
因v0、vt大小都是確定的,由(4)式知,要使面積S最大,應使sin(θ+α)=1,即θ+α=90°,此時,由(3)、(4)式有
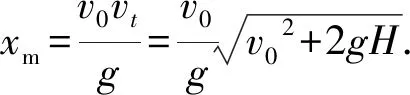
因OAB是直角三角形,有

