規范作圖動態分析 突破組合磁場臨界問題
——以2018年江蘇卷第15題為例

李春亞

(河北辛集中學,河北 辛集 052360)

帶電粒子在組合磁場中運動的問題,綜合性較強、過程復雜．在分析處理此類問題時,要充分挖掘題目的隱含信息,利用題目創設的情景,對粒子做好受力分析和運動過程分析．例如2018年江蘇高考物理題第15題,考查了帶電粒子在組合磁場中的運動,第(1)問大部分學生能完成,第(2)問多數能完成,第(3)問對學生提出的能力要求較高,問題設計有層次,既考查了運動電荷在磁場中勻速圓周運動的基本規律,又涉及了磁場中的臨界問題,對應用數學工具運算和分析極值均有較高要求，可以讓不同層次的考生都能得到相應的體現;較好地考查了核心素養中“科學思維”,便于高校人才選拔．

通過高中階段的學習,學生應具有建構理想模型的意識和能力;能正確運用科學思維方法,從定性和定量兩個方面進行科學推理、找出規律、形成結論,并能解釋自然現象和解決實際問題;具有使用科學證據的意識和評估科學證據的能力,能運用證據對研究的問題進行描述、解釋和預測;具有批判性思維的意識,能基于證據大膽質疑,從不同角度思考問題,追求科技創新．[1]

1 試題解析及拓展

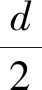
(1) 求磁感應強度大小B；

(2) 入射速度為5v0時，求粒子從O運動到O′的時間t；

(3) 入射速度仍為5v0，通過沿軸線OO′平移中間兩個磁場(磁場不重疊)，可使粒子從O運動到O′的時間增加Δt，求Δt的最大值．

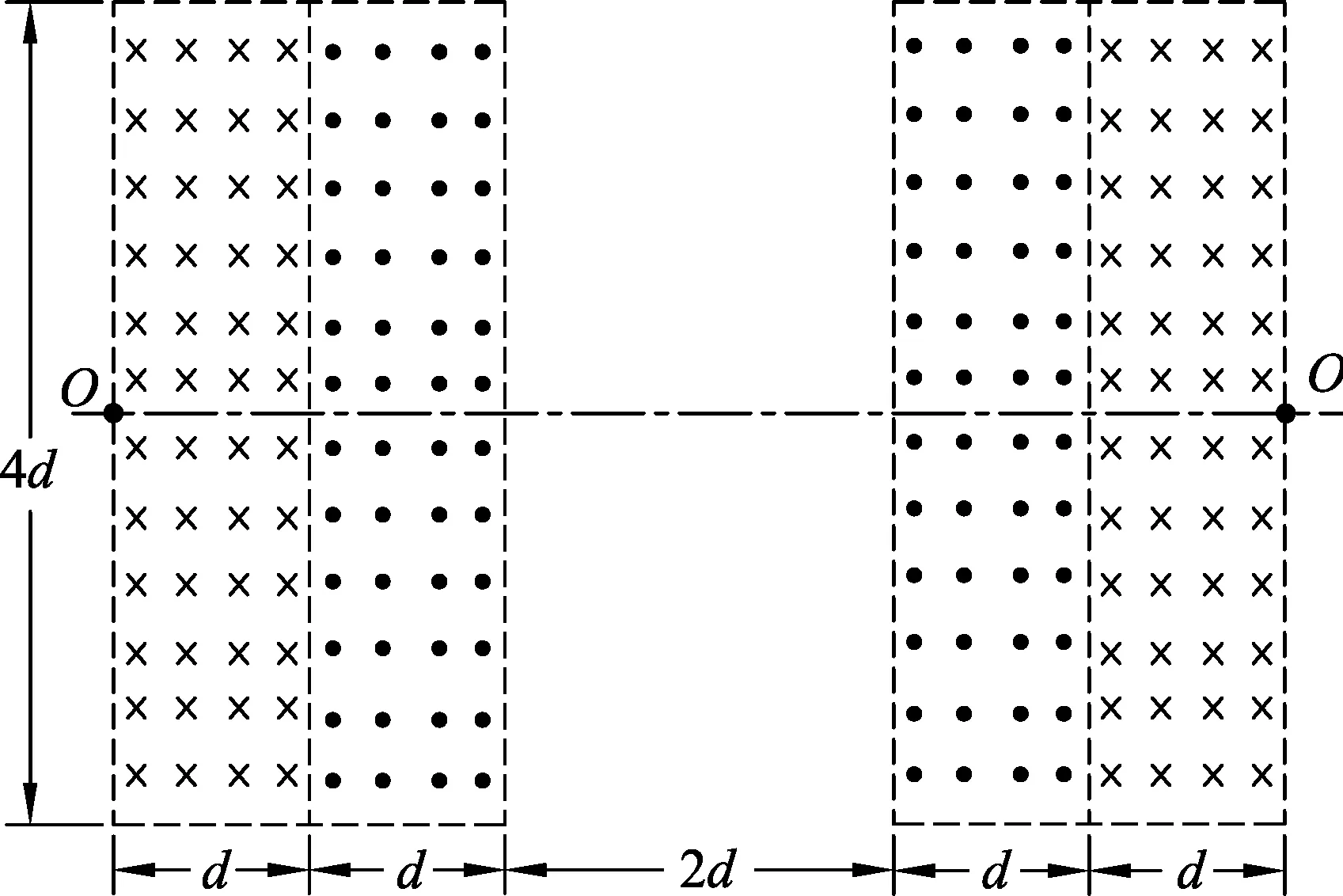
圖1

解析：重點對第(2)、(3)問分析.

第(2)問.設粒子在矩形磁場中的偏轉角為α.

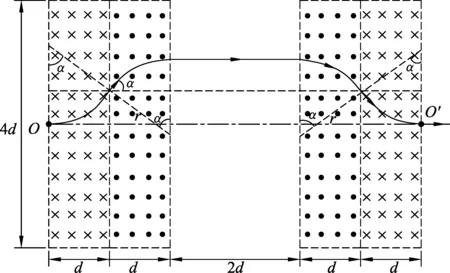
圖2

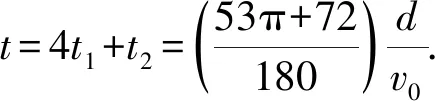
本小題求解時，只要學生嚴格按照帶電粒子在勻強磁場中的解題步驟：定圓心-定半徑-定軌跡-定圓心角，并使用圓規直尺等作圖工具，細致畫圖，結合必要的結論“勻速圓周運動中速度的偏向角等于對應軌跡的圓心角(回旋角)”，就可觀察出軌跡的左右對稱性，并順利得出幾何關系和計算出運動時間.

第(3)問.解法1：(函數分析法)如圖3所示，將中間兩磁場分別向中央移動距離x.

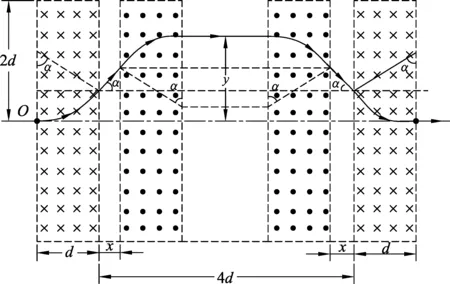
圖3

觀察幾何關系知，粒子向上的偏移量為

y=2r(1-cosα)+xtanα,

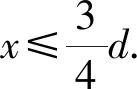
粒子直線運動路程的最大值為

增加路程的最大值為Δsm=sm-2d=d.

解法2：(動態圖形極值分析法)為便于說明，從左向右數分別命名為第1-4磁場區域.觀察圖形可知，隨著第2磁場區域的向右移動，第2磁場區域中的圓弧頂端不斷向上移動，直至頂端與第2磁場區域上邊界相切(如圖4所示)，此時對應的x為最大磁場移動距離.令第3磁場區域向左移動相同距離.(如果第2磁場移動距離比圖4中x還大，那么粒子就會斜向射出第2磁場區域，不會到達第3磁場區域，如圖5所示)

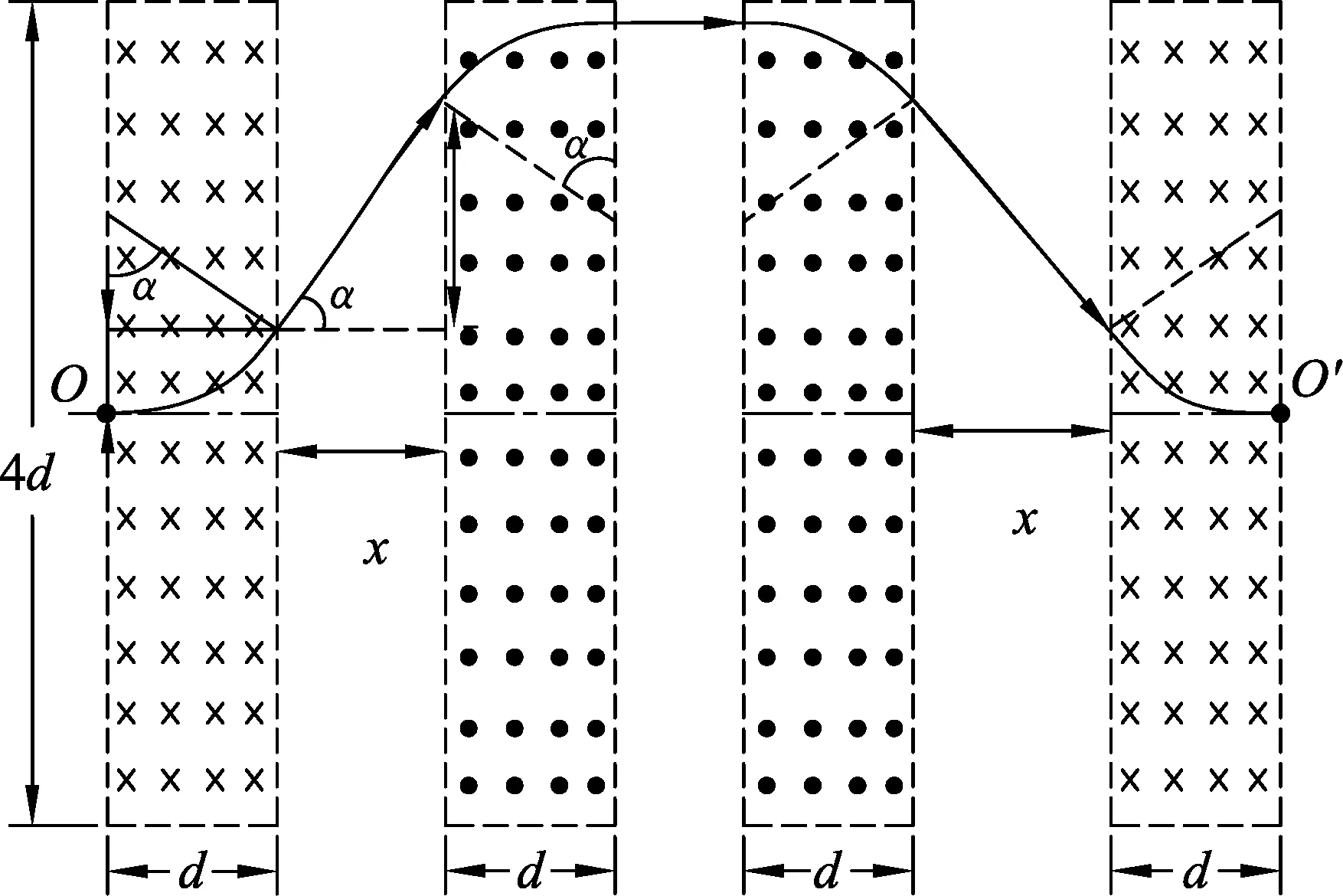
圖4 圖5

所以 ，增加時間的最大值為

相比之下，動態圖形極值分析減少了設出的未知量的個數，更直觀、簡便，學生更易接受.

本題中最易出現的錯誤是，認為中間兩個磁場區域緊挨(但不重疊)時的運動時間增加最多.這樣雖然使斜向直線運動的位移最大，但是注意x′不等于x，這樣就會導致粒子從磁場4中射出時，出射點不在O′，如圖6所示.而題干中明確要求“可使粒子從O運動到O′”.所以在草稿紙上規范畫出清晰的軌跡，有利于避免該種錯誤解法.(拓展)如果原題中去掉“從O′處射出”，只需從第4磁場右邊緣處射出，其余條件不變，則

(1)本題第(3)問又當如何求解？

(2)出射點的位置距離O′最近距離？

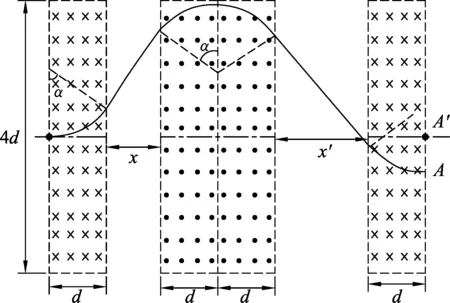
圖6

解析：(1) 如圖6所示，只需從第4磁場右邊緣處射出，那么第2與第3磁場向中央移動的距離就不一定相等，又因為在非磁場中速度為5v0不變，所以當斜向勻速直線運動路程最長時，增加時間最長為

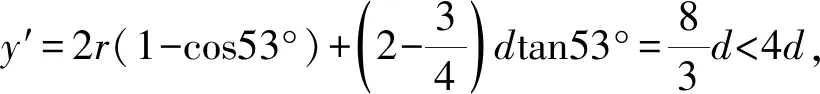
2 反思總結

組合磁場中的臨界問題歷來是高考的重難點，如2016年江蘇卷15題、2015年天津第12題，2014年廣東卷第36題，2014年江蘇卷第14題等，這些題目的難點往往在因變量(速度、入射點位置、或粒子的比荷，以及例如本題中的x)改變后，導致某個或某些物理量(本題中的出射點位置、在非磁場中的運動時間)的改變.那么，如何在教學中，使學生形成解決此類問題的策略呢？

2.1 重視審題過程

遇見較復雜問題時，題干往往較長，過程多、符號多，學生讀題時，容易不得要點.在教學中，教師要有意識地培養學生讀題的好習慣，善于提取關鍵信息，例如“剛好、恰好”“全過程”等等要進行圈畫；已知物理量集中標在草稿紙一處，以便最后檢查.重點概念要在心中默背出其內容，“位移”還是“路程”等等；出現多電場、磁場區域時，要結合審題加以嚴格區分，究竟這些場的邊界在哪？電場強度、磁感應強度是否方向大小已知？是否存在對稱性軌跡？這樣才能體現嚴謹的思維，正確全面地建立起物理情景.本文第(3)問中最易出現的錯誤解法，如果不仔細讀題，也是很難將其回避掉的.

2.2 規范作圖動態分析

在最初講授帶電粒子在勻強磁場中的運動時，教師就要以身作則，從規范板書和板畫開始，培養學生利用作圖工具，規范作圖的習慣.許多磁場中的問題，畫出軌跡，再添加上必要的輔助線，就容易找出相關的幾何關系.涉及到動態分析的，進行圖形移動，并觀察(例如上題中第(3)問的第2種解法)，問題便易于解決了.例如2014年江蘇卷第14題中的畫軌跡步驟(見圖7).

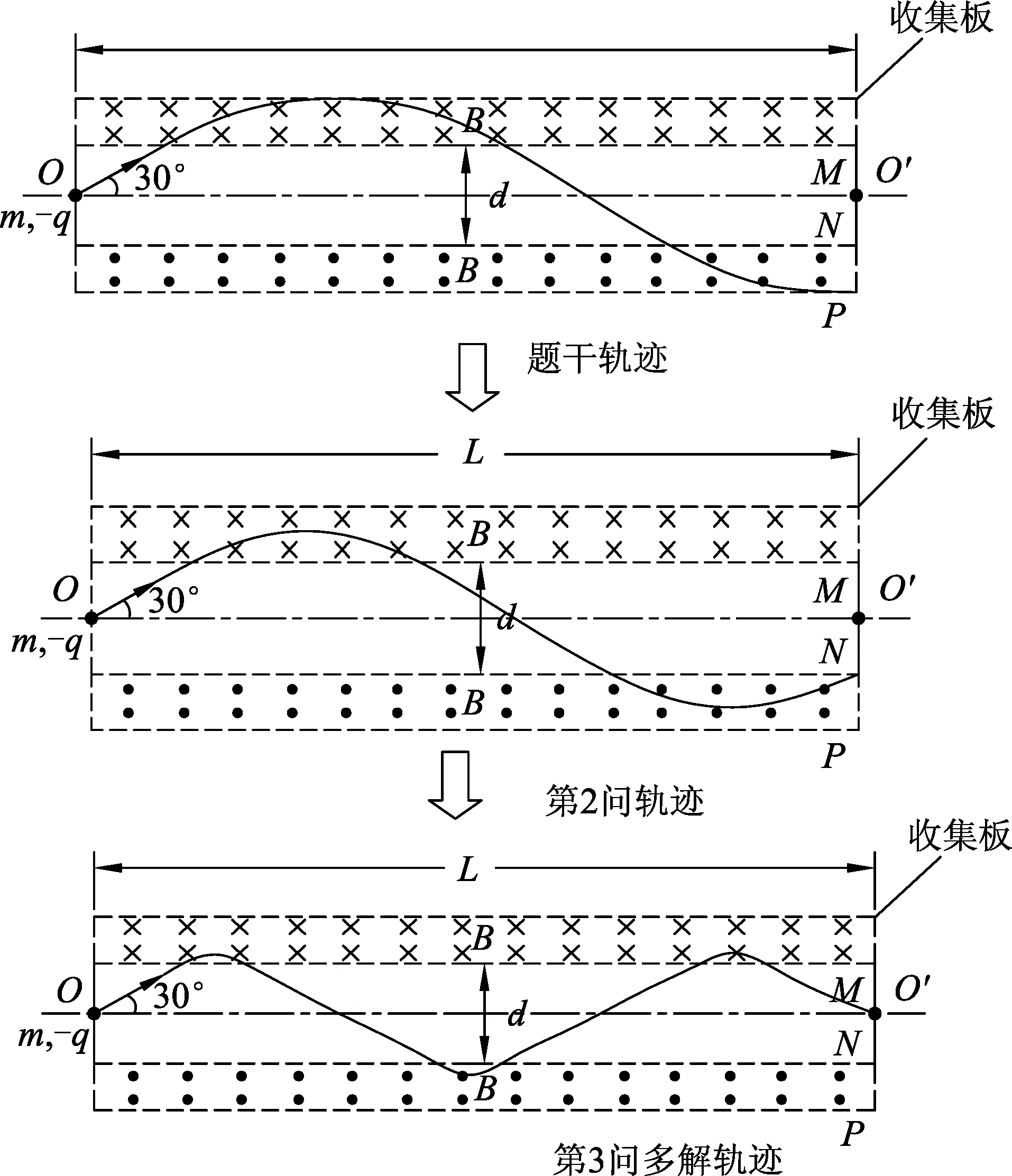
圖7

2.3 加強常見臨界情況的訓練

帶電粒子剛好穿出或剛好不穿出磁場的條件是帶電粒子在磁場中運動的軌跡與邊界相切．解題關鍵是從軌跡入手找準臨界點．

(1) 當粒子的入射方向不變而速度大小可變時，由于半徑不確定，可從軌跡圓的縮放中發現臨界點．

(2) 當粒子的入射速度大小確定而方向不確定時，軌跡圓大小不變，只是位置繞入射點發生了旋轉，可從定圓的動態旋轉中發現臨界點．

(3) 對磁場移動類問題，要發現帶電粒子的軌跡半徑周期等等有沒有改變，找出不變量，并進行動態的畫圖分析，就能找出臨界點.如果作圖發現不了臨界點，那么就結合必要的數學函數推導極值.

2.4 創設開放式、多元化的學習環境

教師在物理課堂教學過程中應該多創設開放式、多元化的學習環境，這樣的學習環境才能突出學生為主體的平等對話和知識建構，突出學生積極獨立思考、形成批判性和創造性思維，才能培養團隊協作、共同探究、實事求是的科學素養，培養有責任和擔當的人才，從而達到踐行物理核心素養理念，實現對人的價值的體現和喚醒.[2]