相干信源DOA估計的一種改進空間譜估計算法

任生凱，劉尚鈔，王開斌，周瑞青

(1.中國航天科工集團二院二十五所,北京 100854；2.中國人民解放軍駐航天二院二八三廠軍事代表室，北京 100854)

0 引言

戰場上，反輻射導彈可以利用敵方雷達的電磁輻射信息進行跟蹤導引，引導反輻射導彈飛行目標，摧毀敵方雷達及其載體，因而在戰爭中具有重要地位。但是隨著現代戰爭的發展，戰場環境日益復雜，受多徑反射、敵方設置的有源誘餌干擾等因素影響，戰場上同一時間、同一空域有時會出現多個相干信源，給反輻射導彈的目標來波方向(DOA)估計、目標跟蹤等能力帶來巨大挑戰。研究如何有效解決多個相干信源的DOA估計問題，對提高反輻射導彈抗干擾能力、提升作戰性能有重要意義。

為解決多個信源的DOA估計問題，從20世紀70年代末開始，超分辨空間譜估計在理論研究方面便出現大量成果，最有代表性的是Schmidt提出的多重信號分類(MUSIC)[1]算法以及Roy、Paulraj和Kailath提出的旋轉不變子空間(ESPRIT)[2-3]算法。人們對這些算法的深入研究促進了子空間類算法的興起。子空間類算法真正意義上實現了角度的超分辨估計，極大提高了DOA估計精度。但是，當面對相干信源時，絕大多數傳統子空間類算法的性能迅速下降，甚至完全失效。

在相干信源情況下，要正確估計出信號方向，關鍵是如何有效地恢復陣列數據協方差矩陣的秩。目前關于解相干的處理大致可分為2類：降維處理和非降維處理。降維處理算法主要包括空間平滑類算法[4]、矩陣重構類算法[5-6]。降維類算法實現簡單且解相干效果較好，但它們是以犧牲陣列的有效孔徑為代價，導致陣列可分辨的最大相干信源數目變少。非降維處理算法包括Toeplitz算法[7]、最大似然(ML)[8]估計和加權子空間擬合(WSF)[9]算法等。其中Toeplitz算法的估計性能較差，ML和WSF算法思想簡單且估計性能優越，但它們在求解過程中涉及到全局多維優化問題，計算過程相當復雜。

本文針對反輻射導彈的典型應用場景，對經典MUSIC算法的陣列接收數據模型進行了修正，提出一種改進的空間譜估計算法——MUSIC-TM。在相干信源情況下，MUSIC-TM算法破壞了經典MUSIC算法接收數據協方差矩陣各列之間的相關性，使其恢復為滿秩，因而具有在反輻射導彈典型應用場景下解相干信源的能力，且計算復雜度無明顯增加。使用Matlab軟件對MUSIC-TM算法進行仿真，驗證了該算法在實際應用中的可行性。

1 系統模型及經典MUSIC算法

基于MUSIC-TM算法的測向系統組成框圖如圖1所示。系統由接收天線陣列、多通道接收機、模數變換模塊和內置了MUSIC-TM測向算法的數字信號處理器組成。接收天線陣列接收到多個信源來波信號，將其送入多通道接收機。信號在接收機中經過變頻、放大，再經過模數變換模塊得到數字信號，送入數字信號處理器，經過MUSIC-TM測向算法處理后，最終得到對來波方向(DOA)的估計。

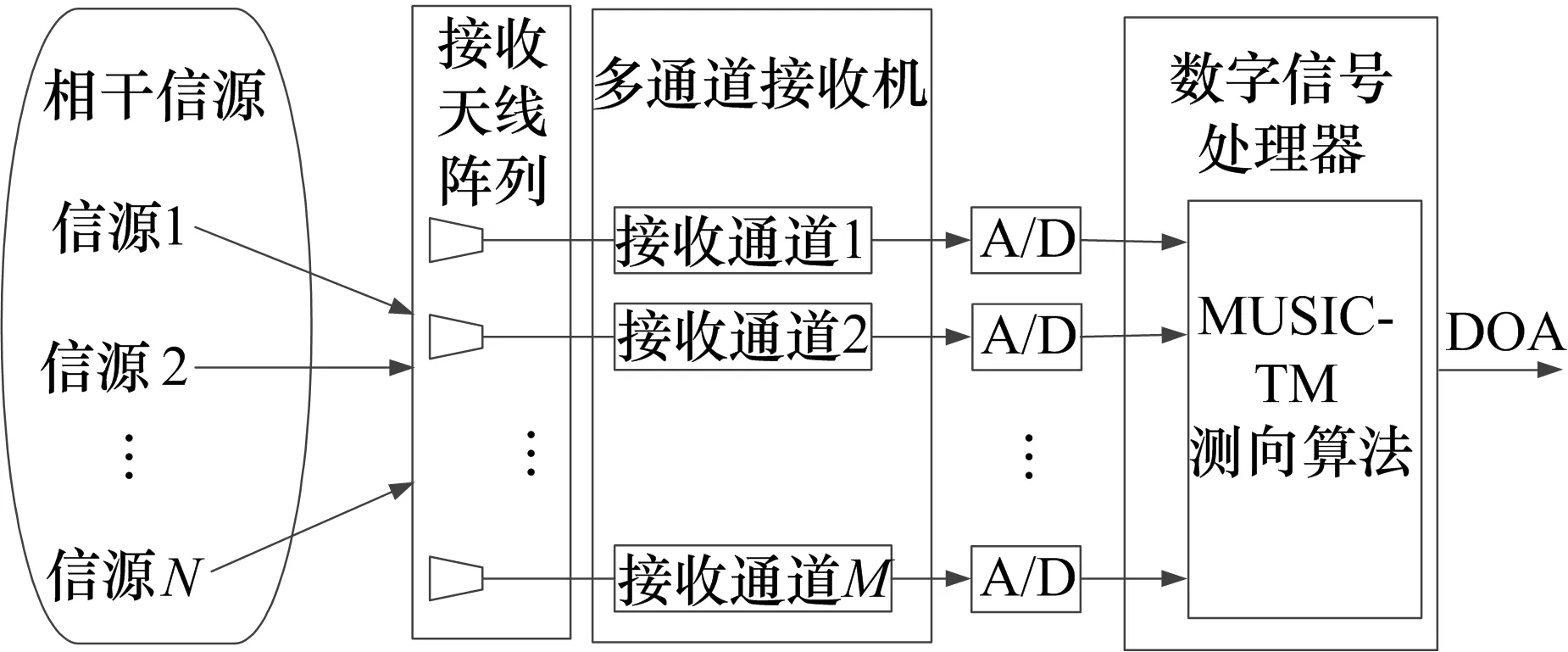
圖1 系統組成框圖

1.1 相干信源模型

對于2個平穩信號si(t)和sk(t)，定義它們的相關系數為：

(1)

由Schwartz不等式可知|ρik|≤1，因此，2個信號之間的相關性定義為：

1)當ρik=0時，si(t)和sk(t)相互獨立；

2)當0<|ρik|<1時，si(t)和sk(t)相關；

3)當|ρik|=1時，si(t)和sk(t)相干。

因此，根據上面的定義可以得到，當2個信號是相干信號時，它們滿足式(2)：

si(t)=wisk(t)

(2)

式中，wi為一個復常數。

1.2 陣列信號模型

大部分研究者對MUSIC算法的研究多以一維均勻線陣為模型，但在反輻射導彈實際應用場景中，接收天線陣列安裝方式一般為平面陣而非線陣，同時，目標信源可能的來波方向也分布在二維空間。因此，本文采用均勻環形陣列布局方式建立接收天線陣列模型，該陣列形式在國外反輻射導彈上較為常見。

考慮N個遠場的窄帶相干信號入射到由M個陣元組成的某空間環形陣列上(假設陣元數等于通道數)，其中各個信源來波方向分別為(φ1,θ1),(φ2,θ2),…,(φN,θN)，波長為λ，φ為方位角，θ為俯仰角。

信號源是窄帶信號，因此信號可用如下形式表示：

(3)

式中，ui(t)是接收信號的幅度，ω0=2πf=2πc/λ是來波信號角頻率，φ0是來波信號的初相。

因為窄帶信號源是遠場的，且信號源與接收天線陣列間相對位置關系不隨時間變化，則有：

ui(t-τ)≈ui(t)

(4)

所以有式(5)成立：

si(t-τ)≈si(t)e-jω0τ,i=1,2,…,N

(5)

則可以得到第l個陣元的接收信號為：

(6)

式中，gli為第l個陣元對第i個信號的增益，τli為第i個信號到達第l個陣元時相對參考陣元的時延，nl(t)為第l個陣元在時刻t的噪聲。理想條件下，不考慮陣列中各陣元的各向異性、通道不一致、互耦等因素的影響，可以認為式(6)中的增益gli相等，這里將gli歸一化為1。

將M個陣元在時刻t接收到的信號寫成一個列矢量，即：

(7)

τli僅與(φi,θi)有關，故式(7)可簡寫為：

X(t)=A(φ,θ)S(t)+N(t)

(8)

又由于s1(t),s2(t),…,sN(t)為相干信號，故式(8)可進一步簡化為如下的矢量形式：

X(t)=A(φ,θ)Ws1(t)+N(t)

(9)

式中，X(t)為M×1維的陣列數據矢量，N(t)為M×1維的陣列噪聲數據矢量，W為N×1維的復常數矢量，A(φ,θ)為M×N維的陣列流型矩陣(導向矢量矩陣)，即：

A(φ,θ)=[a1(φ,θ),a2(φ,θ),…,aN(φ,θ)]

(10)

式中，導向矢量ai(φ,θ)=[e-jω0τ1i,e-jω0τ2i,…,e-jω0τMi]H，i=1,2,…,N。

1.3 經典MUSIC算法

經典MUSIC算法的基本思想是將任意陣列輸出數據的協方差矩陣進行特征值分解，從而得到與信號分量相對應的信號子空間和與信號分量相正交的噪聲子空間，然后利用信號子空間與噪聲子空間的正交性來估計信號來波方向等參數。該算法基于子空間分解思想，算法的基礎是陣列采樣協方差矩陣的特征值分解，算法的目標是計算空間角度譜。

陣列信號模型如式(7)所示，則陣列輸出數據的協方差矩陣[1]為：

R=E[XXH]=AE[SSH]AH+E[NNH]=

ARSAH+RN

(11)

式中，RS=E[SSH]為信號協方差矩陣，RN=E[NNH]為噪聲協方差矩陣。

對R進行特征分解：

(12)

式中，US為大特征值對應的特征矢量矩陣，稱為信號子空間；UN為小特征值對應的特征矢量矩陣，稱為噪聲子空間。

理想條件下，信號子空間與噪聲子空間是正交的，那么信號子空間的導向矢量也與噪聲子空間正交，即：

aH(φ,θ)UN=0

(13)

經典的MUSIC算法正是根據式(13)這個性質提出的。但在具體應用中，考慮到實際接收數據矩陣是有限長的，只能得到采樣數據協方差矩陣，即協方差矩陣的最大似然估計：

(14)

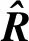
(15)

所以，MUSIC算法的DOA估計公式為：

(16)

根據信號參數范圍進行譜峰搜索，找出極大值點對應的角度就是信號入射方向，這就是理想情況下的經典MUSIC算法。經典MUSIC算法一般只適用于理想條件下，而對于相干多源信號，經典MUSIC算法的理論基礎不再成立。

2 MUSIC-TM算法

但是，1.2小節在推導公式(8)時，無形中假設了在陣列數據采樣過程中，多個相干信源與接收天線陣列間相對位置關系不隨時間變化這一前提。然而，考慮到反輻射導彈的典型應用場景，導彈在飛行過程中，每個信源到反輻射導彈接收天線陣列間的距離Li(i=1,2,…,N)都在時刻變化，且由于每個信源實際分布在空間不同位置上，故每個Li隨時間的變化率不完全同步。此時，公式(7)中的τli不再僅與(φi,θi)有關，還同時與時間t有關，據此公式(9)修正為：

X(t)=A(φ,θ,t)Ws1(t)+N(t)

(17)

式中，A(φ,θ,t)為修正后的陣列流型矩陣(導向矢量矩陣)，即：

A(φ,θ,t)=[a1(φ,θ,t),a2(φ,θ,t),…,aN(φ,θ,t)]

(18)

這種對陣列接收數據模型進行修正后的MUSIC算法即為MUSIC-TM算法。

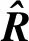
需要注意的是，MUSIC-TM算法中T的取值不能過大，否則在一次快拍采樣過程中各個信源的來波方向將發生明顯偏移，影響最終DOA估計的準確性。

3 性能仿真分析

為了驗證MUSIC-TM算法的有效性，采用Matlab進行建模仿真。仿真場景中，假設反輻射導彈沿某一彈道向待打擊的目標飛去，4個目標信源分布在反輻射導彈飛行方向前下方的地面上，并呈近似菱形分布，示意圖如圖2所示。

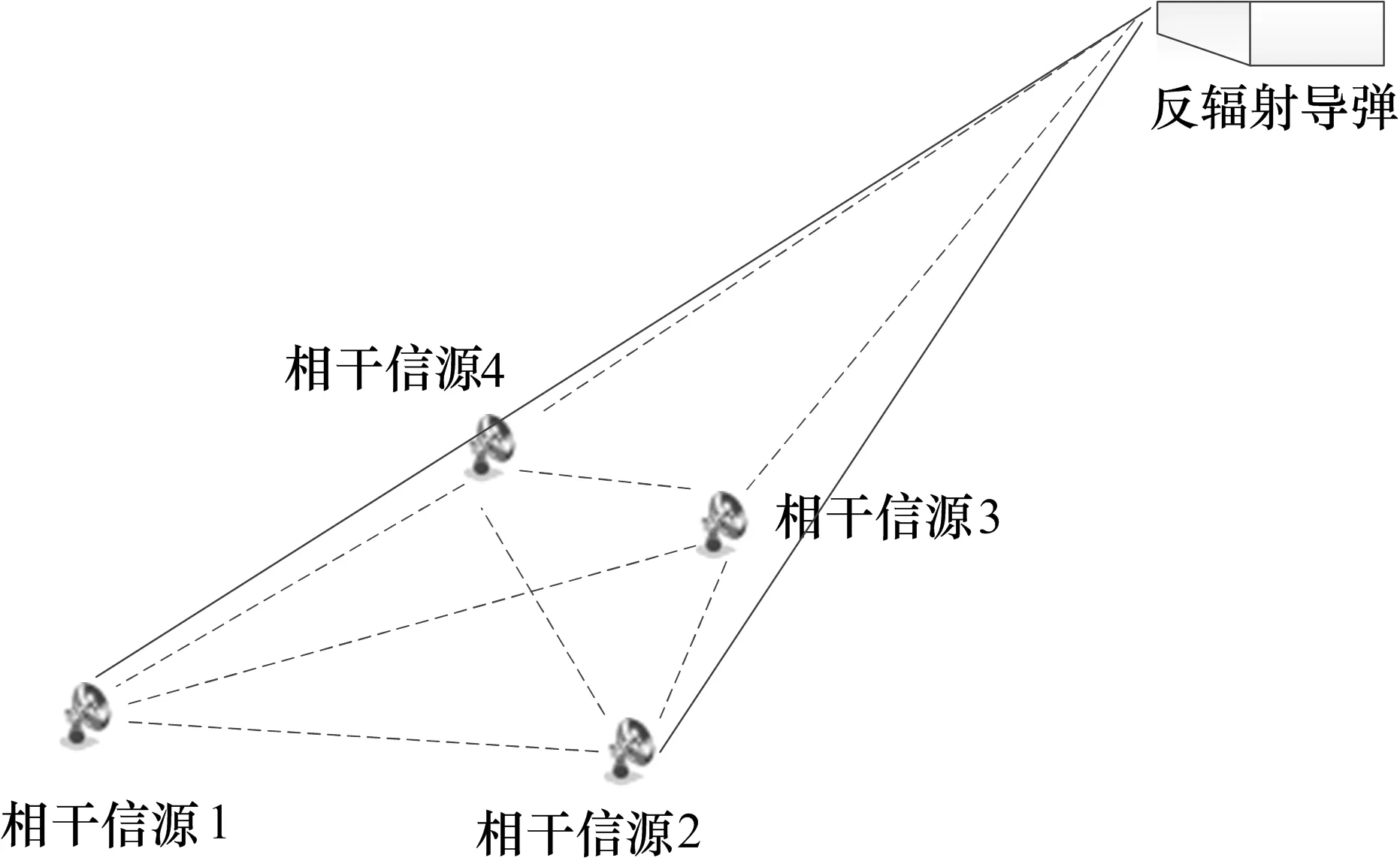
圖2 仿真場景示意圖

3.1 經典MUSIC算法仿真結果

在仿真中，令陣元數M=8，均勻環形陣列的直徑為d=λ，目標信號源數N=4，C波段，噪聲為均值為0、方差為1的高斯白噪聲，信噪比20 dB，快拍數K=1000，采樣快拍持續時間T=5 ms。經典MUSIC算法的仿真結果如圖3所示。

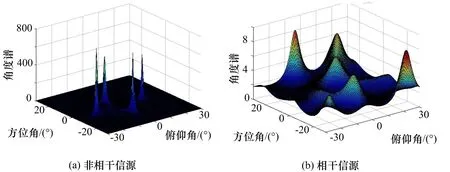
圖3 經典MUSIC算法譜峰搜索結果

圖3(a)為非相干信源下的譜峰搜索結果，圖3(b)為相干信源下的譜峰搜索結果。由圖3(a)可知，4個信源方向均呈現出較尖銳譜峰，說明經典MUSIC算法對非相干多源有較好的DOA估計能力。由圖3(b)可知，當4個信源是相干信源時，譜峰搜索結果未在4個目標信源方向呈現出明顯譜峰，譜峰搜索結果失敗，說明經典MUSIC算法對相干多源沒有DOA估計能力，這一結果與理論分析一致。

3.2 MUSIC-TM算法仿真結果

仿真參數設置與3.1小節中經典MUSIC算法相同，MUSIC-TM算法的仿真結果如圖4所示。

圖4 MUSIC-TM算法譜峰搜索結果

圖4(a)為非相干信源下的譜峰搜索結果，圖4(b)為相干信源下的譜峰搜索結果。與圖3(b)不同，當4個目標信源是相干信源時，在圖4(b)中MUSIC-TM算法的譜峰搜索結果仍然呈現出4個較尖銳的譜峰，說明MUSIC-TM算法在相干信源DOA估計方面的性能遠優于經典MUSIC算法。

由圖4(a)可知，MUSIC-TM算法也同樣可以對非相干信源進行DOA估計，其性能與經典MUSIC基本相同，符合理論分析的預期。

綜上所述，MUSIC-TM算法具備一定的工程應用價值。

4 結束語

本文對經典MUSIC算法的陣列接收數據模型進行了修正，提出一種改進的空間譜估計算法MUSIC-TM，并通過Matlab仿真對MUSIC-TM算法的解相干信源能力進行了測試。仿真結果表明，在反輻射導彈典型應用場景下，MUSIC-TM能夠克服經典MUSIC算法無法對相干信源進行準確測向的缺陷，對相干信源具有較好的DOA估計能力，為反輻射導彈抗多徑干擾和相干有源干擾提供了一種有價值的方案。■