LFM雷達移頻干擾時域補償技術研究

李金炳，史小偉，陳俊霖

(電子信息控制重點實驗室，四川 成都 610036)

0 引言

線性調頻脈沖壓縮雷達通過相關接收技術，較好地解決了雷達作用距離與距離分辨率之間的矛盾，在現代雷達中得到了廣泛的應用[1]，如何有效地干擾脈沖壓縮雷達也是當前研究熱點之一。目前干擾脈壓雷達的主要手段是利用其距離與多普勒之間的強耦合關系[2]，當回波信號發生多普勒頻移時，在脈壓結果上會產生測距誤差。其常規實現方式主要是利用數字射頻存儲器(DRFM)轉發雷達信號，轉發時在接收到的雷達信號的基礎上調制一定的多普勒分量，即可實現對脈壓雷達的干擾。楊紹全等人利用脈壓信號在時間和多普勒間的強耦合關系，提出了用移頻干擾實現欺騙干擾的方法[1]。劉建成等人建模分析了干擾機產生的干擾信號相對于接收的雷達信號的群延遲[3]，文獻[4]在此基礎上設計了階梯波移頻、線性函數移頻、分段線性函數移頻干擾技術。本文將以雷達為出發點建立干擾回波模型，分析幾種干擾相對真實目標的延時，進而提出時域補償方法實現對目標完全覆蓋的壓制干擾。

1 脈沖壓縮原理及典型移頻干擾

對于典型LFM雷達,其發射信號可表示為：

S=Arect(t-τ/2,T)exp(j2πf0t+jπKt2),

t∈[0,T]

(1)

式中，f0為信號初始頻率，K=B/T為信號調頻斜率，B為Chirp信號帶寬，τ為脈寬，T為信號周期，rect(·)為矩形函數。對于位于距離R0處的一靜止目標，其回波信號可表示為：

Sr=ARrect(t-τ/2,T)·

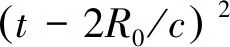
(2)

式中，AR為幅度調制系數。通常，匹配濾波器是雷達處理接收機一個重要的組成部分，脈沖壓縮是目標檢測的關鍵環節。設濾波器函數為h(t)，對于輸入信號s(t)，其輸出可以表示為：

y(t)=s(t)*h(t)

(3)

式中，*為卷積運算。y(t)是一個辛格函數，其最大值出現在R0所對應的時刻。雷達以此得到目標距離信息。

下面分析單假目標移頻干擾原理。移頻干擾是在雷達信號上調制一個或多個頻率值，使雷達脈壓處理結果出現虛假目標的干擾方式。單假目標移頻干擾是干擾機在接收到的雷達信號的基礎上調制一個單點頻，忽略干擾機延時，單假目標移頻干擾模式下雷達接收信號可表示為：

Sr-j0=Aj0rect(t-τ/2,T)exp(j2πf0(t-2R0/c)+

(4)

式中，fj0為單點頻干擾信號頻率值，式(4)表示干擾信號與目標回波同時進入雷達接收機的情況下干擾信號的表達式。其掃頻特性如圖1所示。

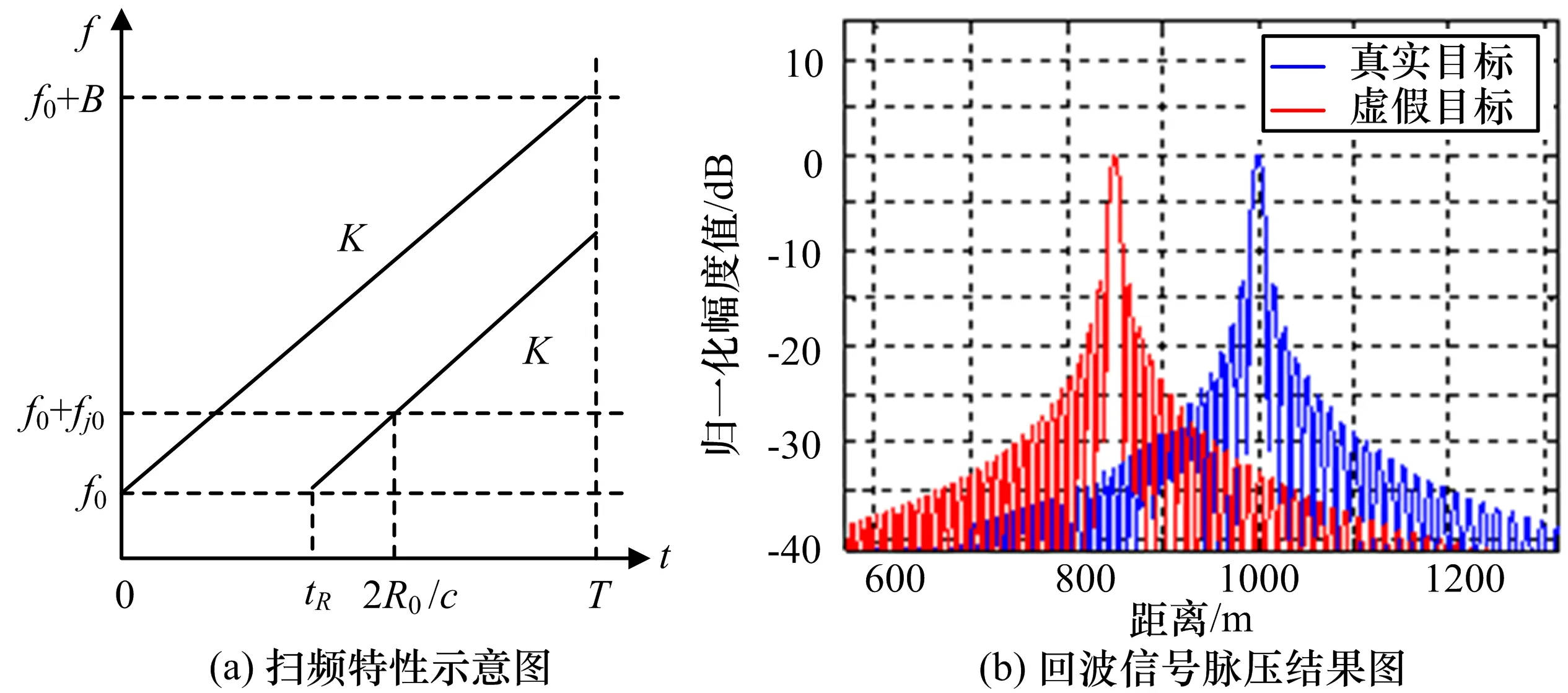
圖1 單假目標移頻干擾掃頻特性及干擾效果示意圖

由圖1可以得到虛假目標出現位置所對應的時刻tR=2R0/c-fj0/K，當fj0>0時，假目標相較于真實目標位置前移，反之則滯后于真實目標。

2 階梯波調制移頻干擾

階梯波調制移頻干擾是在單假目標移頻干擾基礎上，把整個脈沖寬度T均分為N段，每段的時長為Δt，相鄰“階梯”之間的頻率差為Δf，每段“階梯”的頻率值為fjn=fj0+nΔf，其中n=0,1,2，…，N-1。和單假目標移頻干擾類似，每個Δt所對應的干擾頻率對應一個假目標，該假目標與真實目標之間的時延為Δtn=fjn/K。匹配濾波器的通帶范圍將限制調頻范圍：|fjn|≤B，此處B表示濾波器的通帶邊界。圖2給出了Δf為正時的掃頻特性示意圖，以及其所對應的干擾示意圖。

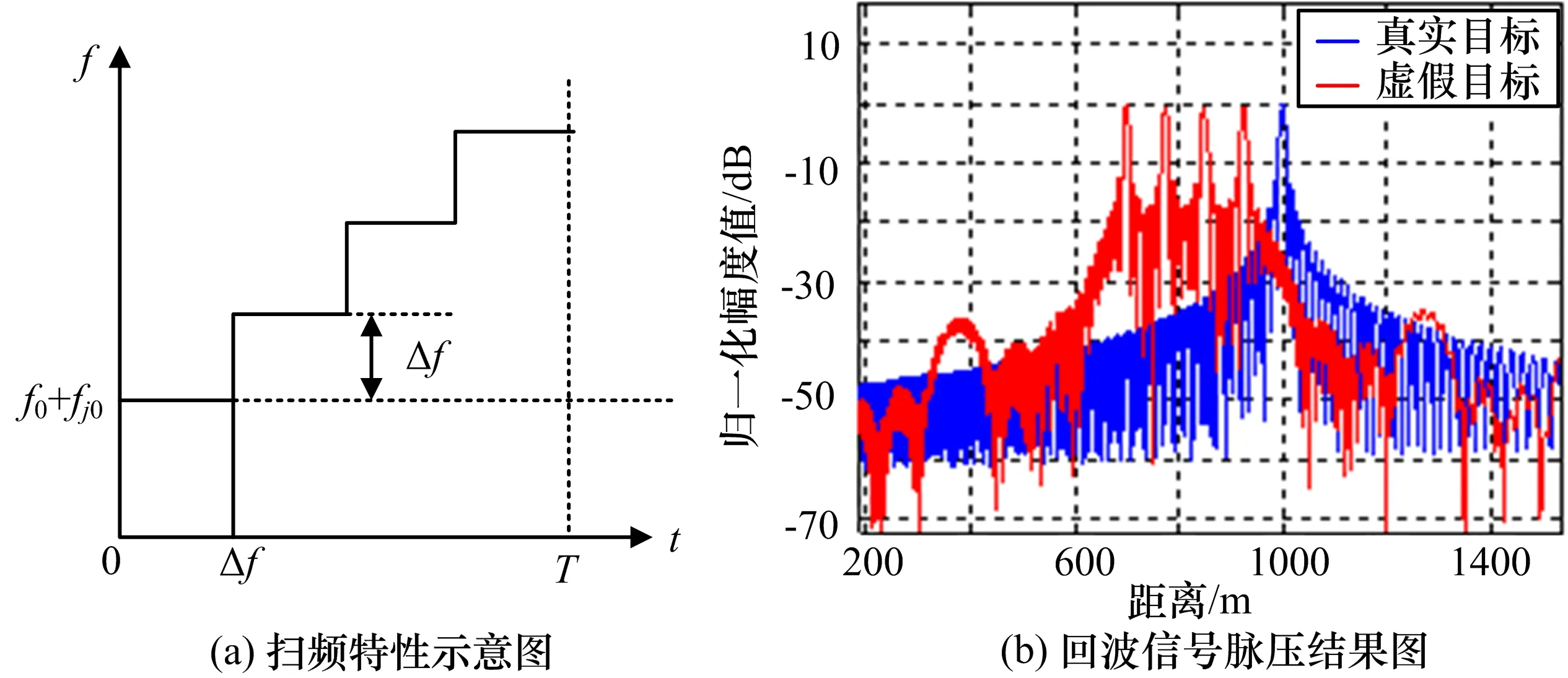
圖2 階梯調頻掃頻特性及干擾效果示意圖

與單假目標同理，當干擾調制頻率fjn>0時，假目標相對于真實目標將前移；當fjn<0時，假目標則滯后于真實目標。在干擾頻率滿足濾波器通帶范圍情況下，假目標群中心位置與真實目標之間的時差為：tcenter=(fj0+fjm)/(2K)，fjm為滿足通帶頻率要求的最大干擾頻率。

2.1 線性調頻移頻干擾

文獻[4]對干擾機接收與發射信號進行了分析，給出了干擾機發射信號的模型。這在雷達干擾中是不足夠的，因為對于雷達而言，回波中的干擾信號是否對目標信號檢測產生影響才是干擾是否有效的判斷準則。以下將以雷達接收機為基準建模分析干擾進入雷達接收機的效果。

為方便分析，重寫雷達發射線性調頻信號：

S=Arect(t-τ/2,T)exp(j2πf0t+jπKt2)

(5)

對于普通線性調頻干擾，設干擾信號起始干擾頻率為fj0，干擾調制頻率Kj。在自衛干擾中，對于位于距離R0的目標，忽略干擾機自身時延，雷達接收到的干擾回波為：

Sr-K=AKrect(t-τ/2,T)exp(j2π(f0+fj0)

(6)

式中，AK為幅度調制系數。

雷達接收機接收到的信號是在發射信號的基礎上延遲并調制后的結果，由上述線性調頻干擾表達式可知，線性調頻干擾可以看作是在單假目標干擾的基礎上調制線性調頻干擾，為推導簡便，推導初始干擾調頻頻率fj0=0的情況，如圖3所示。

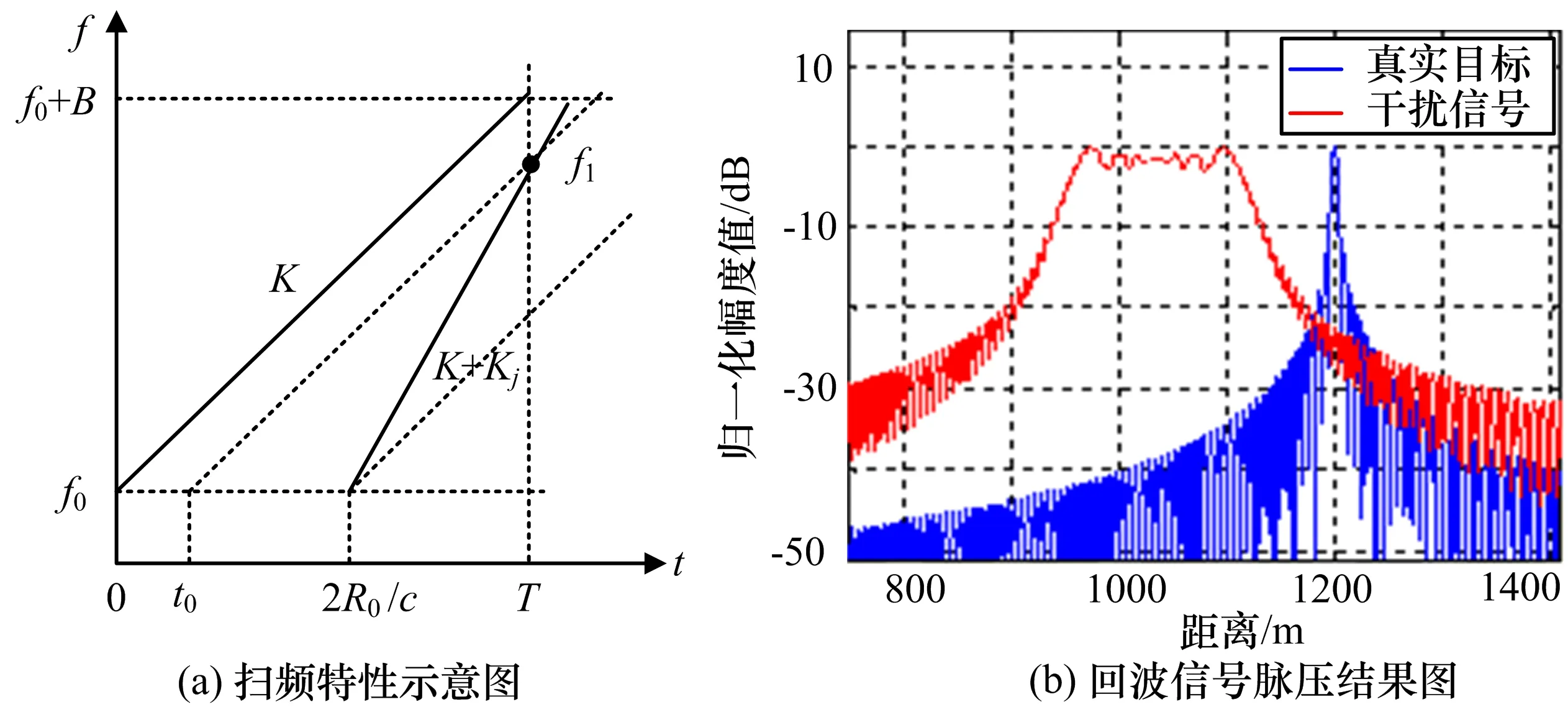
圖3 線性調頻掃頻特性及干擾效果示意圖

雷達接收機的匹配濾波器的通帶范圍是參考信號所對應的帶寬，通帶頻率范圍為[f0,f0+B]，干擾信號經濾波器后的輸出頻率范圍也必須滿足該約束條件。并且由于雷達脈壓處理的周期性，回波信號經過濾波器的有效時間將變短。如圖3所示，距離為R0處干擾回波信號到達雷達接收機的時刻為2R0/c(忽略干擾機處理時延)；由于濾波器時域周期性，干擾信號通過濾波器的最大頻率為f1。當干擾調制斜率過大，將會使干擾信號通過濾波器的最大頻率為f0+B，此處不具體分析，原理與圖3一致。頻率為f1的干擾信號經過匹配濾波器時，其等效的起始時刻由濾波器固有調頻斜率決定，起始時刻為t0。所以干擾信號經過濾波器的時間邊界為[t0,t1]：

t1=2R0/c

(7)

t0=(B-(T-2R0/c)(K+Kj))/K

(8)

由式(7)、(8)可得干擾信號的時域中心點：Δt=(t0+t1)/2，即干擾信號相對于真實目標回波的延時，這即是上述脈壓結果中干擾信號相對于真實目標回波的時間差。同理當Kj<0時，干擾目標將滯后于真實目標。

2.2 常規線性函數移頻干擾效果分析

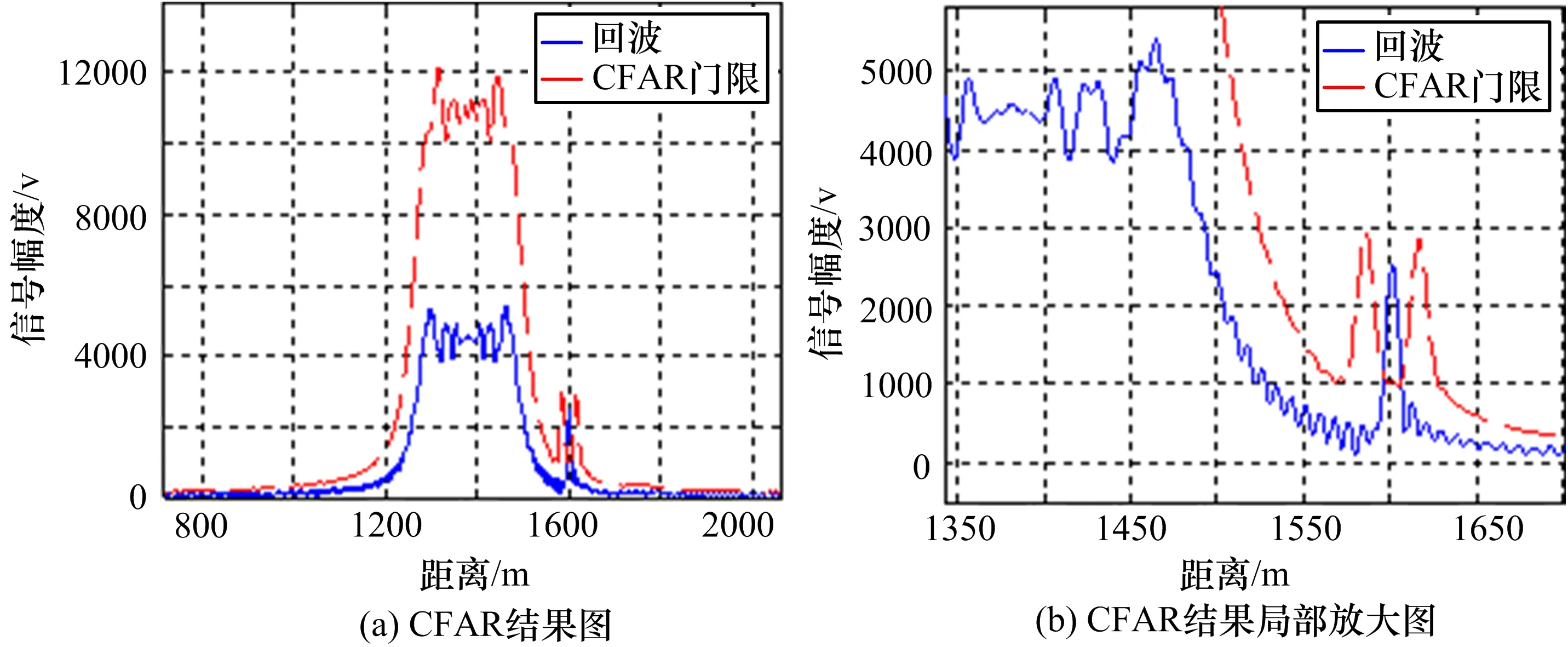
圖4 干擾剔除示意圖(右圖為左圖局部放大結果)

由上述分析可知，幾種移頻干擾均可產生假目標群以達到欺騙雷達的效果。但是由上述干擾仿真圖可知，由上述幾種干擾方式產生的假目標相對真實目標均會存在一定的時差。由其模糊函數可知，這正是由于線性調頻信號存在距離和多普勒之間強耦合關系導致的。雷達可以利用該時差實現抗干擾，在使用滑動窗CFAR[5]檢測時，即可將干擾“剔除”。以線性調頻移頻干擾為例，圖4給出雷達利用假目標與真實目標間的距離差實現抗干擾的實例。

圖4中，目標出現在1600 m位置附近，假目標群出現在目標前方。合理設置CFAR算法參數，目標將能很好的被檢測出。干擾假目標被雷達“剔除”掉，失去其干擾的作用。

3 移頻干擾延遲優化研究

由上述分析可知，假目標群和真實目標回波之間的時差是干擾信號在對應的干擾調制模式下，經傳輸時延以及雷達接收機的匹配濾波器的綜合作用下產生的。為了避免雷達檢測算法(以CFAR為例)有效剔除干擾信號，可對干擾信號進行時域補償，使干擾信號的假目標群臨近于真實目標，下面將研究將假目標群中心與真目標(起始時間點2R0/c)對準的方法，使之完全掩蓋真實目標，達到覆蓋的干擾效果。圖5給出K′>K的情況，其它情況分析類似。

為分析簡便，圖5給出了干擾起始調制頻率fj0=0的情況。斜率為K′的實線是接收機收到的帶有干擾調制的回波經時域補償后的信號示意，虛線為干擾信號中心頻點與匹配濾波器匹配的示意。為使干擾中心在脈壓結果圖上對準目標，干擾中心頻率f1通過匹配濾波器時，由濾波器斜率調制后所對應的時刻“零點”對準目標回波起始時刻t0=2R/c。由圖5可得：

f1=f0+K(t2-2R/c)=f0+K′(t2-t1)

(9)

f2=f0+K′(T-t1)

(10)

解幾何關系可以得到干擾信號的起始時刻t1：

t1=(T(K′-K)+4R0/cK)/(K+K′)

(11)

同理易得起始調制頻率fj0≠0時的補償時間Δt：

4R0/cK)/(K+K′)

(12)

Δt=t1-2R0/c

(13)

式中，K′=K+Kj。那么，干擾機在生成信號時，在雷達信號的基礎上增加時間延遲Δt，使雷達接收機收到的信號為：

Sr-j0-Δt=AK′rect(t-τ/2,T)exp(j2π(f0+fj0)·

(14)

通常，如果干擾信號幅值與信號幅值一致，那么這種補償的方法將使目標回波同時抬高，以致干擾無效。解決辦法是使用帶阻濾波器將濾除干擾信號中對應目標位置的頻譜，降低干擾信號的匹配濾波結果中目標位置所對應的脈壓結果幅值；并適當增大干擾信號功率，相較于普通壓制干擾，增加的功率是極其微弱的。

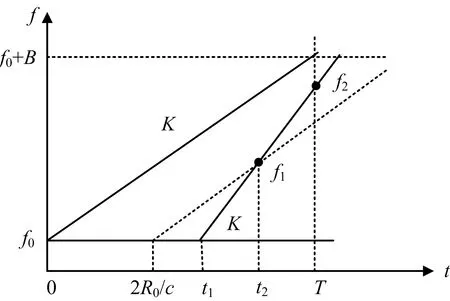
圖5 線性調頻模式的掃頻特性示意圖

4 仿真驗證

為驗證上述方法的有效性，選用文獻[7]中的參數進行仿真：T=100 μs，B=10 MHz，fs=30 MHz，載波頻率f0=10 MHz；干擾機起始調制頻率fj0=1 MHz，調頻斜率Kj=5 kHz/μs，設置目標位置R0=6km。圖6是其仿真結果。圖6中，在未加補償時，目標群中心出現在4275 m位置，與上面分析的結論一致。在增加延時補償后，干擾信號相較于補償后移，假目標群中心與真實目標回波重合。

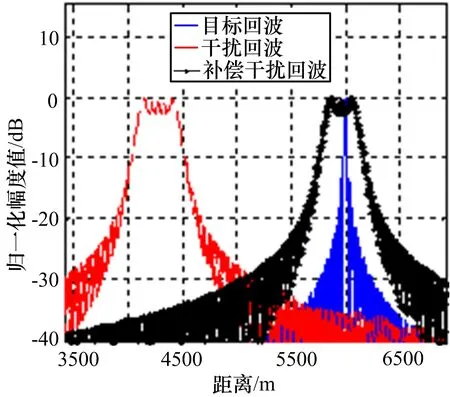
圖6 干擾效果對比示意圖

圖7是補償干擾信號經帶阻濾波器后的干擾效果仿真。圖7(a)中，當時域補償后的干擾信號經帶阻濾波器后，對應目標位置(1200 m)處的幅值明顯降低，若阻帶范圍增加，則幅值下降更加明顯。圖7(b)是濾波后的干擾信號放大5倍后的脈壓結果和目標回波脈壓結果，可見，目標回波被完全“淹沒”在干擾信號中，達到了壓制干擾的目的。

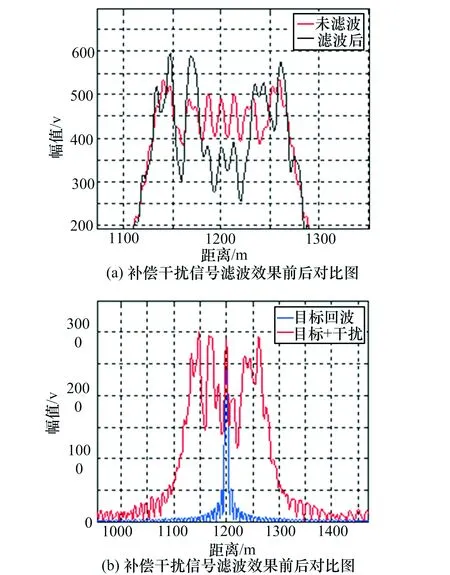
圖7 補償干擾信號經濾波器處理效果

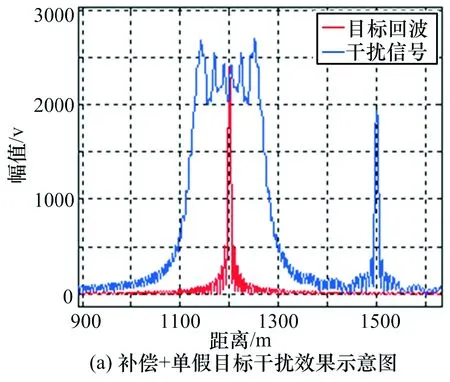
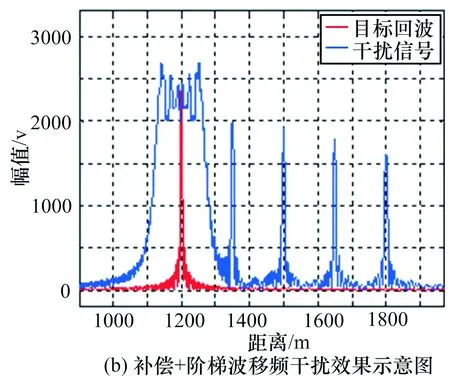
圖8 時域補償+假目標干擾示意圖

若在對線性調頻干擾補償的基礎上再施加常規假目標干擾即可實現“欺騙”雷達的目的。圖8即是在補償干擾的基礎上分別疊加單假目標和階梯波移頻干擾的仿真結果，圖8(a)是在線性調頻移頻干擾的基礎上疊加單假目標干擾的仿真，圖8(b)是疊加階梯波調頻干擾的結果。在兩仿真結果中，經延時補償的線性調頻移頻干擾的干擾中心與目標重合，并在時域上形成大范圍覆蓋，成功干擾雷達對真實目標的檢測。同時，在距目標后方形成單假目標實現對雷達的欺騙干擾。

5 結束語

本文通過研究典型移頻干擾在雷達接收機進行脈壓處理后產生的假目標相對真實目標存在時間差的問題，分析了幾種常規移頻干擾模式下時間差產生的原因，驗證了常規線性函數移頻干擾對CFAR檢測算法失效的可能。提出了對線性函數調頻移頻干擾進行時域補償的一種干擾方法，實現了對真實目標完全覆蓋的壓制干擾。并在此基礎上疊加普通點頻單假目標干擾或階梯波移頻干擾，實現在施加壓制干擾的基礎上對雷達進行欺騙干擾。■