基于模式函數和變分法的螺旋槳最佳環量計算方法

韓用波，周偉新，董鄭慶，馮 君，董世湯

(1. 中國船舶科學研究中心，江蘇 無錫 214082；2. 中船重工（上海）節能技術發展有限公司，上海 200011)

0 引 言

螺旋槳能夠將70%左右的機械動力轉化為推進力，成為當前各類船舶上應用最為廣泛的推進器形式。對于民船螺旋槳，特別是散貨船、油船和集裝箱船等三大主流船型，推進效率是這類船舶螺旋槳設計時最優先考慮的指標。在螺旋槳主參數確定后，螺旋槳的效率主要由其徑向環量分布決定。開展螺旋槳最佳徑向環量的研究可以從機理上給出提高推進器效率的方向。因此以效率為目標的螺旋槳最佳環量計算一直是螺旋槳設計研究的一個重要內容。

螺旋槳最佳環量的計算方法是伴隨著升力線理論的發展而提出的。早期，Betz發展螺旋槳升力線理論時，根據在效率較高處增加環量，在效率較低處減小環量的思想，Betz得出了敞水條件下最佳環量分布條件。Lerbs[1]首次提出了求解最佳環量分布的變分法，建立了優化方程式，限于當時的計算條件，未能在計算機上實現。但Lerbs提出的求解最佳環量分布的變分法思想，逐漸成為求解敞開螺旋槳、導管槳、對轉槳等各類組合推進槳葉最佳環量的主流方法，一直沿用至今。近年來，國外關于螺旋槳最佳環量計算方面的研究工作，主要集中在麻省理工學院Kerwin教授及其學生身上[2 – 4]。國內蘇玉民[5]、曹慶明[6]、孫文愈[7]等也采用變分法開展了船用推進器最佳環量計算的研究工作。

采用傳統變分法進行最佳環量分布數值求解時，需要對升力線模型進行離散，將連續的環量分布離散為在渦格內均布的常量，連續的自由渦片離散為從渦格邊界泄出的集中渦。根據Kerwin[8]的研究成果，在使用離散化升力線模型時，在葉梢和葉根2個自由端存在1/2階的奇性，因此需要對2個端部的網格劃分和控制點布置進行特殊處理。本文給出一種求解螺旋槳最佳環量的改良方法，將徑向環量分布用正弦級數表達出來，通過求解正弦級數模式函數的各項系數，從而得到螺旋槳最佳環量分布形式。

1 基本理論

1.1 正弦級數模式函數表達螺旋槳徑向環量分布

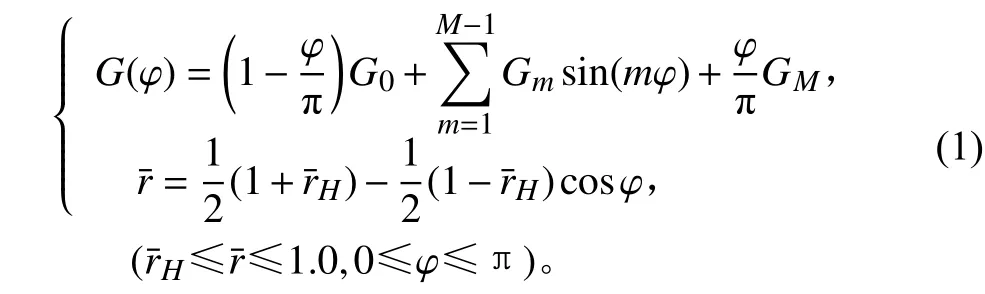
1.2 螺旋槳誘導速度的計算

誘導因子仍按Lerbs的定義不變，則誘導速度的計算式如下：

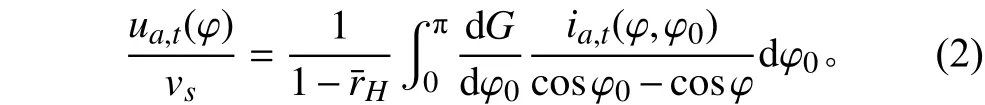
由式（1）可得：

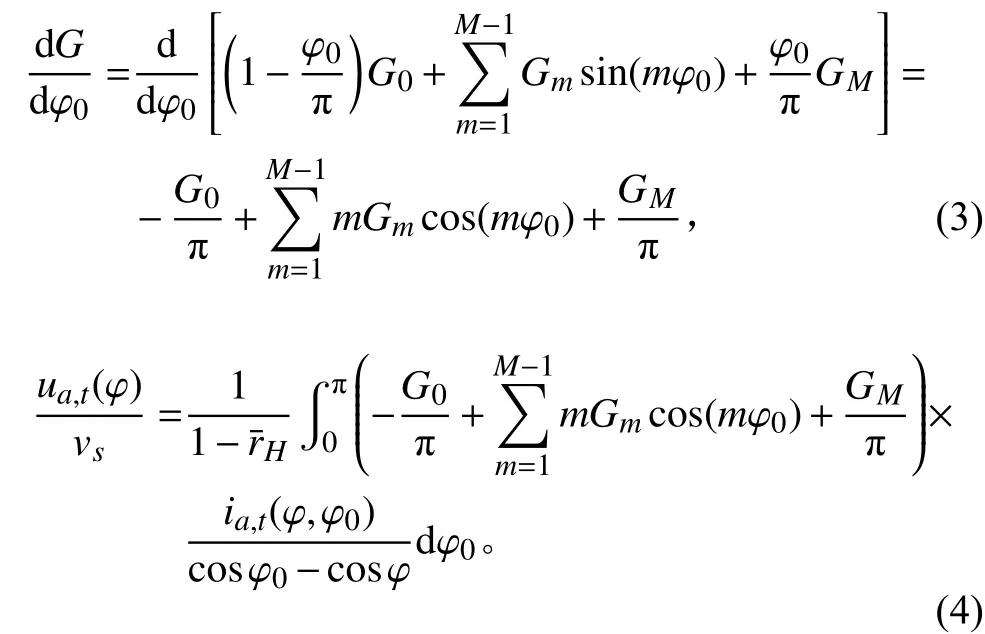
可以將式（4）寫成如下形式：

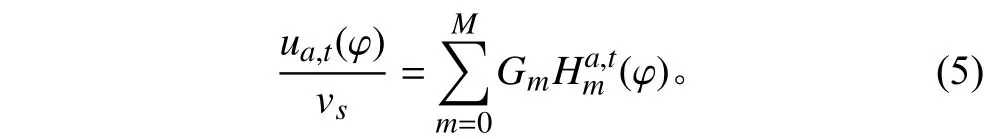
其中：

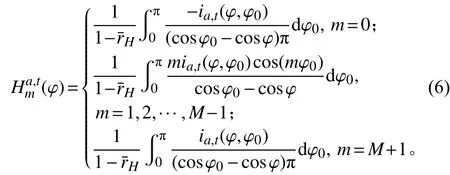
1.3 功率系數和推力系數的計算

將式（1）中的環量分布改寫成如下形式：

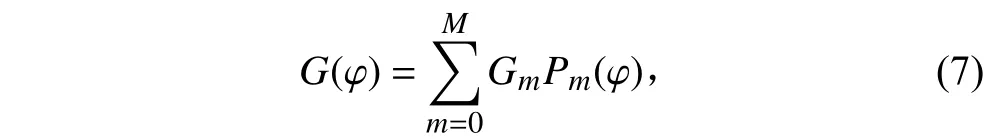
功率系數

令

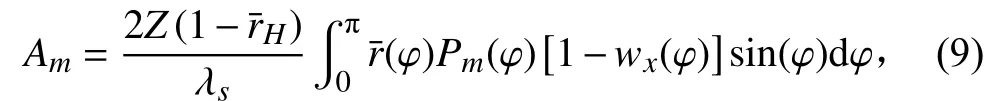
改寫

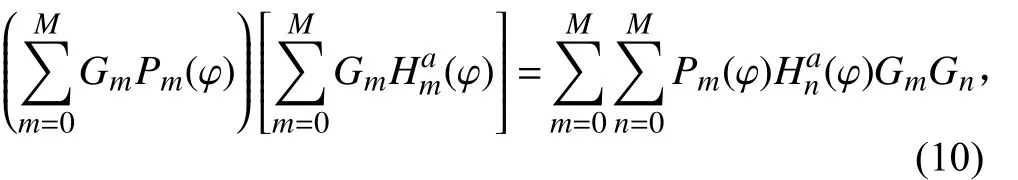
又令

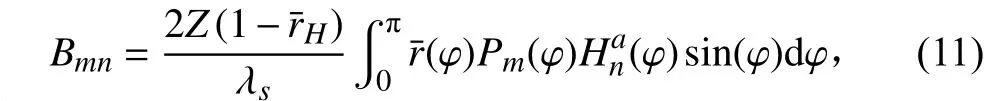
則功率系數計算式可與成以下形式：

同理，推力系數可以寫成如下形式：

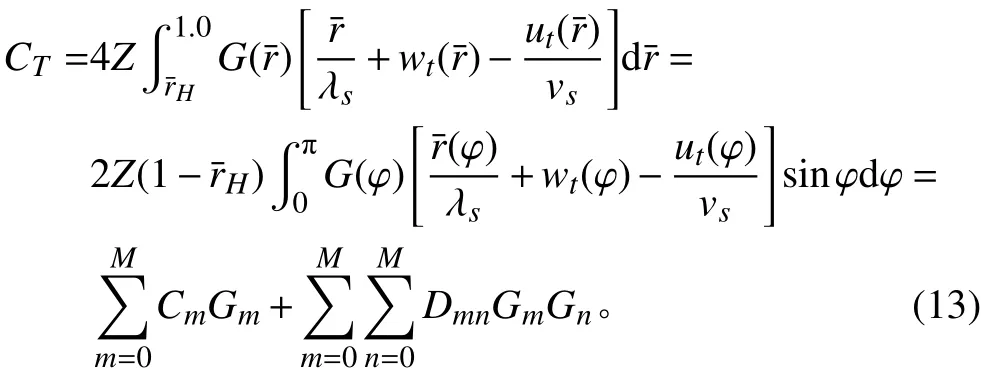
其中：

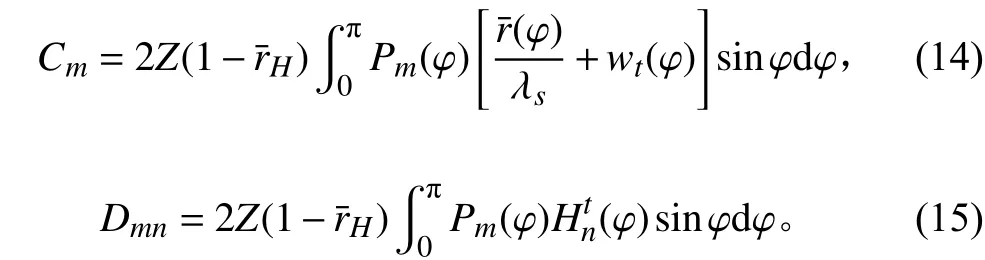
1.4 變分法求解最佳環量

求解最佳環量分布的條件是：推力系數須滿足指定值而功率系數為最小，或功率系數滿足指定值而推力系數最大，這一問題可轉化為多元函數求條件極值的問題。以指定推力系數求的極小值為例，引入Lagrange乘子，并構建輔助函數，則求極值條件的方程式為：

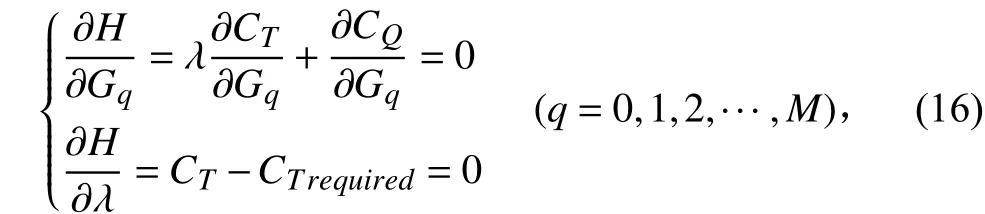
其中：

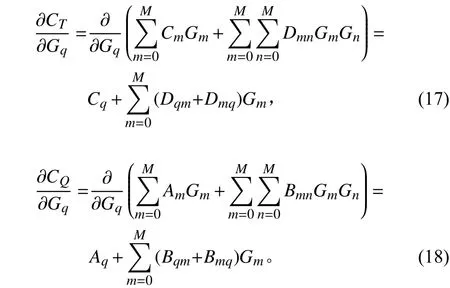
聯立式（16）~式（18）可得：

整理后可寫成：

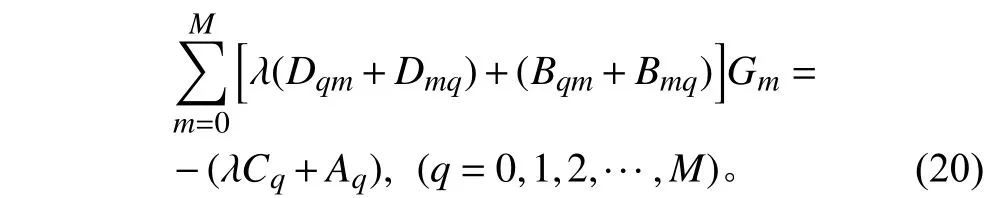
但是，這一輪的過程是建立在某一給定的水動力螺距角分布的基礎上的，故需有迭代過程。在第一輪求解時可以先用進角分布代替水動力螺距角作為初值。在求出表達環量分布的正弦級數各項系數后，重新計算誘導速度和水動力螺距角分布，用新的水動力螺距角分布再重新計算得出新的最佳環量分布，一直迭代到和誘導速度收斂。至此方求出表達最佳環量的正弦級數各項系數的最終值后，代入式（1）最佳環量分布得解。

2 算例驗證

編制求解螺旋槳最佳環量程序，選取Coney[6]在1989年博士論文中給出的2個案例進行計算和對比。

考核案例1：均勻來流條件下螺旋槳最佳環量分布計算比較。

5葉螺旋槳，轂徑比0.2，不考慮槳轂和粘性影響，不考慮尾渦變形和收縮，敞水工況，Ct=0.512，計算 J=0.1，0.2，0.4，0.6，0.8，1.0，1.2 和 1.4 時的最佳環量分布。計算對比結果見圖1（a）。

考核案例2：周向平均的軸向伴流分布條件下螺旋槳最佳環量分布計算比較。

5葉螺旋槳，轂徑比0.2，不考慮槳轂和粘性影響，不考慮尾渦變形和收縮，Ct=0.307，J=1.377，計算周向平均的軸向伴流下螺旋槳最佳環量分布。計算對比結果見圖1（b）。關于本案例中具體的伴流分布可參見文獻[9]。

從圖2可以看出，敞水和伴流條件下的最佳環量計算結果均和Coney的計算吻合良好，表明本文基于正弦級數和變分法的螺旋槳最佳環量分布計算方法是可行和正確的。

為對本文所述方法的數值穩定性進行考核，針對案例2，在升力線模型離散時采用不同網格數量和網格劃分方式進行最佳環量的計算，對比結果如圖2所示。可以看出，計算結果并未因網格數量和劃分方式的不同而發生較大跳動，該方法的數值穩定性良好。

圖 1 與 Coney 計算的最佳環量分布結果比較Fig. 1 Comparisons of the optimum circulation distribution calculated in this paper and by coney

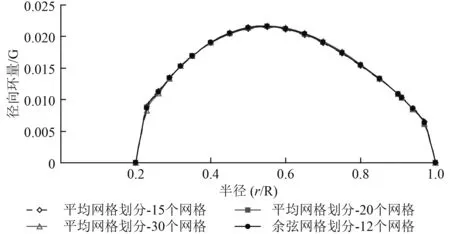
圖 2 不同網格數量和網格劃分方式下最佳環量計算結果比較Fig. 2 Comparisons of optimal circulation calculation results under different number of mesh grids and mesh methods

3 結 語

本文介紹一種基于正弦級數模式函數和變分法的螺旋槳最佳環量計算改良方法，并編寫相應的計算程序。算例驗證表明，計算結果并未因為網格數量和劃分方式的不同而發生較大跳動，該方法的數值穩定性良好，計算結果正確。本文的最佳環量改良計算方法有效和可行，可用于螺旋槳的效率優化及工程設計。