提高回歸模型擬合優度的策略(Ⅲ)
——校正均值變換與其他變量變換

胡良平

(1.軍事醫學科學院研究生院，北京 100850；2.世界中醫藥學會聯合會臨床科研統計學專業委員會，北京 100029

1 問題的提出

1.1 “算術均值變換”有改進的余地

本期科研方法專題的《提高回歸模型擬合優度的策略(Ⅱ)——算術均值變換與其他變量變換》一文(以下簡稱“前文”)提出了對“多值名義自變量(包括多值有序自變量)”進行“算術均值變換”的處理方法，配合其他變量變換方法(指對定量自變量與因變量的多種變量變換方法)，較好地提高了回歸模型的擬合優度。然而，“算術均值變換”有改進的余地。因為在計算多值名義自變量各水平組中定量因變量的均值時，其“隱含前提條件”是“沒有其他自變量”或“其他自變量的影響完全相同”。事實上，在具有多自變量的回歸分析資料中，除了“多值名義自變量或多值有序自變量或二值自變量”外，還有多個“定量自變量”，而且，沒有理由認為這些“定量自變量”滿足前面述及的“隱含前提條件”。需要借助“協方差分析”的計算方法消除“其他定量自變量”對定量因變量的影響。此時，求出的“多值名義自變量”各水平下“定量因變量的均值”被稱為“校正均值”。采用“校正均值”取代“算術均值”的方法被稱為“校正均值變換”法。

1.2 用“校正均值變換”取代”啞變量變換”

1.2.1 何為“校正均值變換”

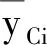
求“校正均值”的具體方法是借助“協方差分析”，在方差分析模型中，分組變量為“多值名義自變量”，它是一個“定性影響因素”，再將其他的定量自變量一同寫入“一般線性模型”，以“定量因變量”為協方差分析的“因變量”。在獲得“協方差分析”結果之前，需要計算出“消除了其他定量自變量影響”條件下“定性影響因素”各水平下“定量結果變量”的均值，它們被稱為“校正均值”。

1.2.2用“校正均值變換”取代“啞變量變換”的合理性

前文已用了較大篇幅陳述了用“算術均值變換”取代“啞變量變換”的合理性。由上面的內容可知，“校正均值”比未校正的“算術均值”更合理。故用“校正均值變換”取代“啞變量變換”的合理性，也就不言而喻了。

1.3 實際問題與數據結構

沿用本期科研方法專題第一篇文章《提高回歸模型擬合優度的策略(Ⅰ)——啞變量變換與其他變量變換》中的“實際問題與數據結構”[1]，此處不再贅述。

2 解決問題的思路和做法

2.1 對自變量和因變量的處置方法

2.1.1對“燃油種類(fuel)”這個“6值名義自變量”進行”校正均值變換”

求出“燃油種類(fuel)”各水平下“氧化氮釋放量(nox)”的校正均值所需要的SAS程序如下：

/*下面的SAS程序計算出多值名義變量各水平下定量因變量的校正均值*/

data aa;

set sashelp.gas;

proc glm data=aa;

class fuel;

model nox=fuel cpratio eqratio;

lsmeans fuel;

run;

【說明】上面的“lsmeans語句”就是希望輸出“多值名義自變量(fuel)”各水平下的“校正均值”。

【SAS輸出結果】

校正均值Fuelnox LSMEAN82rongas3.5185295994%Eth2.11619735Ethanol1.95691843Gasohol3.32335605Indolene3.54233497Methanol1.54554003

將“燃油種類(fuel)”的各水平變換成與定量因變量相應的“算術均值”所需要的SAS程序如下：

/*下面的SAS程序將多值名義變量各水平變換成與定量因變量相應的校正均值*/

data a1;

set sashelp.gas;

if fuel=' 82rongas' then mfuel=3.51853;

else if fuel=' 94%Eth' then mfuel=2.11620;

else if fuel=' Gasohol' then mfuel=3.32336;

else if fuel=' Indolene' then mfuel=3.54233;

else if fuel=' Methanol' then mfuel=1.545540;

else if fuel=' Ethanol' then mfuel=1.95692;

run;

通過運行上面的SAS程序，在原數據集sashelp.gas中就增加了一個定量自變量mfuel，將用它取代多值名義自變量“燃油種類(fuel)”。

2.1.2 對定量因變量和自變量的處置方法

“對定量因變量和自變量不做任何變換”“僅對定量自變量做變換”“僅對定量因變量做變換”和“同時對定量自變量和因變量做變換”，這幾種情況的“具體含義”參見“前文”“第2.1.2節至第2.1.5節”，此處從略。

2.2 對定量自變量和因變量進行變量變換的方法

2.2.1對定量自變量進行多種變量變換，以產生派生變量

所需要的SAS程序如下：

/*在數據集a1的基礎上增加定量自變量的各種派生變量18個，形成數據集a2*/

data a2;

set a1;

x1=log(cpration);x2=sqrt(cpration);x3=exp(cpration);

x4=cpratio**2;x5=x4*cpratio;

w1=log(eqration);w2=sqrt(eqration);w3=exp(eqration);

w4=eqratio**2;w5=w4*eqratio;

z1=log(mfuel);z2=sqrt(mfuel);z3=exp(mfuel);

z4=mfuel**2;z5=z4*mfuel;

m1=cpration*eqration;m2=cpration*mfuel;

m3=eqration*mfuel;

run;

運行以上SAS程序后，就創建了數據集a2，它在數據集a1基礎上增加了由三個定量自變量“cpratio”“eqratio”和“mfuel”派生出來的18個新自變量，它們分別是每個定量自變量的自然對數變換、平方根變換、指數變換、平方變換和立方變換的結果；還有三個定量自變量兩兩交叉乘積變換的結果。

2.2.2 對定量因變量進行5種變量變換

所需要的SAS程序如下：

/*在數據集a2的基礎上增加定量因變量的5種變量變換結果，形成數據集a3*/

data a3;

set a2;

y1=log(nox);y2=sqrt(nox);y3=exp(nox);

y4=1/nox;y5=exp(nox)/(1+exp(nox));

run;

運行以上SAS程序后，就創建了數據集a3，它在數據集a2基礎上增加了由定量因變量(nox)派生出來的5個新因變量，它們分別是自然對數變換(y1)、平方根變換(y2)、指數變換(y3)、倒數變換(y4)和Logistic變換(y5)的結果。

2.3 基于“校正均值變換”的建模策略

【說明】在以下的建模策略中，先對多值名義自變量進行“校正均值變換”；然后在以下每種情形中都將分別在“包含截距項”與“不含截距項”的條件下，分別采取“前進法”“后退法”和“逐步法”篩選自變量。

建模策略將由以下六部分組成：①以“氧化氮釋放量(nox)”為定量因變量；②以“氧化氮釋放量的自然對數變換結果(y1)”為定量因變量；③以“氧化氮釋放量的平方根變換結果(y2)”為定量因變量；④以“氧化氮釋放量的指數變換結果(y3)”為定量因變量；⑤以“氧化氮釋放量的倒數變換結果(y4)”為定量因變量；⑥以“氧化氮釋放量的Logistic變換結果(y5)”為定量因變量。以上6種建模策略的具體內容與“前文第2.3.1節至第2.3.6節”完全相同，此處從略。

3 基于“校正均值變換與其他變量變換”的回歸建模結果與評價

3.1 各種回歸建模策略下所得主要結果的匯總

以摘要形式呈現選出的24個擬合較好的回歸模型見表1。

3.2 基于“校正均值變換與其他變量變換”回歸建模效果的分組評價

這部分有六個小標題，其內容與“前文”中相應部分完全相同，詳見“前文第3.2.1節至第3.2.6節”，此處從略。

3.3 對各組模型中挑選出來的最優模型再進行擬合優度的總評價

從以上的“評價結果”可知：模型4、模型8、模型12、模型16、模型20和模型24分別是從6組模型中挑選出來的“最優模型”，現將它們從表1中摘錄出來，以便直觀比較和判斷。見表2。

表1 反映24個多重回歸模型擬合優度的計算結果

注：第1組模型對應的因變量為“氧化氮釋放量(nox)”；第2組模型對應的因變量為“氧化氮釋放量的自然對數變換結果(y1)”；第3組模型對應的因變量為“氧化氮釋放量的平方根變換結果(y2)”；第4組模型對應的因變量為“氧化氮釋放量的指數變換結果(y3)”；第5組模型對應的因變量為”“氧化氮釋放量的倒數變換結果(y4)”；第6組模型對應的因變量為”氧化氮釋放量的Logistic變換結果(y5)”

表2 各組挑選出來的6個“最優”多重回歸模型擬合優度的計算結果

由表2可知：模型24是6個“最優”模型中“最佳”的。該模型的因變量為“氧化氮釋放量的Logistic變換結果(y5)”，從全部(3+18=21個)自變量中篩選出了12個具有統計學意義的自變量，模型中不含截距項。具體計算結果如下：

變量參數估計值標準誤差II 型 SSFPr > FCpRatio-0.305280.151010.002474.090.0449EqRatio-294.7077832.775120.0489080.85<0.0001x21.516950.692470.002904.800.0300x40.004580.002060.003004.970.0273w187.098569.411430.0518085.65<0.0001w2-349.8387438.958570.0487780.64<0.0001w3284.6897431.703120.0487780.64<0.0001w5-130.5704714.465230.0492881.48<0.0001z20.342150.078430.0115119.03<0.0001z50.002360.000988630.003465.710.0180m1-0.024140.002950.0403766.74<0.0001m3-0.132250.018390.0312951.72<0.0001

輸出以上結果的“SAS過程步程序”如下：

/*模型24：R2=0.9992,調整R2=0.9992,MSE=0.00060486,Cp=14.9351,niv=12,無截距項*/

Proc reg data=a3;

model y5=cpratio eqratio mfuel x1-x5 w1-w5

z1-z5 m1-m3/noint selection=backward sls=0.05 r;

/*模型24*/

run;

3.4 小結

在對定量因變量構建多重回歸模型的過程中，摒棄了傳統統計思維下的理論和方法(對定量因變量和定量自變量保持一次方形式，即不做任何變量變換，也不產生派生變量；對多值名義自變量進行啞變量變換，構建所謂的“多重線性回歸模型”)，而引入了動態統計思維下的理論和方法(對定量因變量分別采取不做變量變換和做5種變量變換，即對數變換、平方根變換、指數變換、倒數變換和Logistic變換)；淘汰了對“定量自變量不做任何變換”和“永遠固定為一次方形式”的僵化思維，不僅對其做“對數變換、平方根變換和指數變換”，還引入了“平方項、立方項和交叉乘積項”；本文提出了一種新的變量變換方法，即對“多值名義自變量”進行“校正均值變換”，不僅將其變換成“定量自變量”，還產生出多項派生變量。

由表1和表2可知：基于傳統統計思維創建的回歸模型的擬合效果非常差(模型編號分別為1、5、9、13、17、21)，而基于動態統計思維創建的回歸模型的擬合效果很好(表2中除模型16之外)。其中，“校正均值變換”“引入派生變量”“假定回歸模型中不含截距項”和“找到定量因變量合適的變量變換方法(就本文實例而言，除了‘指數變換’外，其他4種變量變換方法的擬合效果都相當好，其中最佳的是Logistic變換)”是動態統計思維“建模策略”中的核心。

有興趣的讀者可以運用文獻[2-4]中“機器學習”算法，實現本文資料的回歸建模，并將其擬合結果與本文進行比較，從而發現不同分析方法的優缺點。