基于線性正弦跟蹤算法的PMSM無位置傳感器研究

何繼愛，郁 琪，李婕妤，馬 云

(1.蘭州理工大學, 蘭州 730000;2.中山市普陽電子科技有限公司,中山 528400)

0 引 言

內置式永磁同步電機(以下簡稱IPMSM)具有高功率密度、高效率等優點，在工業領域扮演重要角色[1]。在采用磁場定向矢量控制時，為了實現高性能的三相永磁同步電機控制系統，一般都需要獲取準確的轉子位置及轉速信息，但機械傳感器的安裝使用會增加成本，占用空間，并對使用環境有比較嚴格的要求[2-3]。高頻信號注入法的基本思想是把一個高頻電壓(電流)信號疊加到基波信號上，相應的高頻電流(電壓)信號中將攜帶轉子位置信息，通過適當的信號處理就能估計出轉子的位置[4-5]。

目前，常用的注入高頻信號主要有旋轉高頻電壓信號[6]和脈振高頻電壓信號[7]。脈振電壓信號注入法可以用于凸極率很小甚至表貼式永磁同步電機轉子位置檢測，但是轉子位置信息提取的快速性和準確性對高頻注入法位置跟蹤性能有極大的影響。文獻[8-9]設計了基于鎖相環(PLL)的轉子位置跟蹤方法，并將PI調節器和其串聯構成PLL系統，可以快速準確地跟蹤轉子位置。文獻[10]采用基于跟蹤觀測器的轉子位置估計方法，對轉子位置實現了較好的跟蹤。以上方法雖然可以實現轉子位置的快速跟蹤，但是為了獲得角度誤差，要預先對高頻響應電流進行幅值調制和低通濾波處理，增加了運算量。

本文基于脈振高頻電壓信號注入法，對IPMSM模型進行研究分析，將電力系統中對電信號的分析方法線性正弦跟蹤(LST)算法[11]引用到轉子位置跟蹤中，設計了LST位置跟蹤器，不需要對高頻響應電流進行幅值調制和低通濾波，就可以直接提取轉子角度誤差，從而實現永磁同步電機的無位置傳感器控制。

1 脈振高頻電壓信號注入法的原理

1.1 永磁同步電機數學模型

內置式三相永磁同步電機在旋轉坐標系下的電壓方程：

(1)

定子磁鏈方程：

(2)

將式(2)代入式(1)，電壓方程可變成：

(3)

式中：ud，uq分別是定子電壓的d，q軸分量；id，iq分別是定子電流的d，q軸分量；R是定子電阻；ωe是電角速度；Ld，Lq分別是d，q軸的電感分量；ψf代表永磁體磁鏈。

轉矩方程：

(4)

式中：Te為電磁轉矩；p為電機極對數。

1.2 脈振高頻電壓激勵下的永磁同步電動機電流響應

當電機運行于低速區且注入信號頻率遠高于電機運行頻率時，永磁同步電機可以近似等效為純電感模型。此時式(3)可以簡化：

(5)

式中：udh，uqh為d，q坐標系定子高頻電壓分量；idh，iqh為d，q坐標系定子高頻電流分量；Ldh，Lqh為d，q坐標系定子高頻電感。

圖1 幾種坐標系間關系

(6)

式中：

(8)

(9)

(10)

(11)

式中：uin為高頻電壓信號的幅值；ωin為高頻電壓信號的頻率。

此時，式(10)可以簡化：

(12)

將q軸高頻響應電流單獨列寫如下:

(13)

2 線性正弦跟蹤算法

2.1 線性正弦跟蹤的原理

線性正弦跟蹤(以下簡稱LST)算法可以實現對正弦信號幅值和相位的估計，根據最小方差原則和梯度下降法，再經過旋轉變化，得到線性常微分方程，從而設計線性正弦跟蹤器。當輸入正弦信號的角頻率等于濾波器的頻率參數，則濾波器輸出能夠實現對輸入的無幅值誤差、無相位誤差跟隨[10]。目前，LST算法主要應用于電力系統中對電信號的分析。

假設已知頻率為ωo的單個正弦信號表達式：

u(t)=Usin(ωot+δo) (-π≤δo≤π) (14)

(15)

把式(14)展開得到：

u(t)=Ucosδosin(ωot)+Usinδocos(ωot)(16)

(17)

幅值的估計值a(t)：

(18)

信號的估計誤差e(t)：

(19)

根據最小均方誤差思想，定義代價函數：

根據以上分析可以看出，流域內大部分區域作物都存在不同程度作物缺水情況，但是不同分區缺水的原因也有所區別。

(20)

采用隨機梯度下降法，并且每個狀態的變化方向為J(y)對該狀態的梯度的負方向：

(21)

μ為矩陣，調節y(t)收斂到最優值的速度以及算法的穩定性。令μ1>μ2>0，選擇：

(22)

得到周期系數線性動力系統：

y(t)做旋轉變換，令：

(24)

代入式(23)可得：

(25)

(26)

(27)

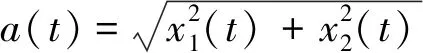
由式(28)可以對信號的幅值進行計算跟蹤。

2.2 LST算法的穩定性證明

(30)

對式(30)進行Laplace變換，有：

對式(31)進行Laplace逆變換，有三種情況：

(1)當μ=2η時，有：

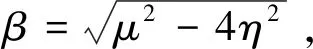
3 仿真與分析

由LST算法直接跟蹤式(13)的高頻響應電流的幅值變化，提取角度誤差值Δθe，并將其調節至0，那么Δθ也將為0，此時轉子位置的估計值收斂到轉子位置實際值。基于LST算法的脈振高頻電壓信號注入法原理，如圖2所示，其中T3s/2s表示三相坐標系轉換到靜止坐標的變換矩陣；T(θe)表示靜止坐標系轉換為旋轉坐標系的變換矩陣；T-1(θe)為旋轉坐標系轉換為靜止坐標系的變換矩陣。

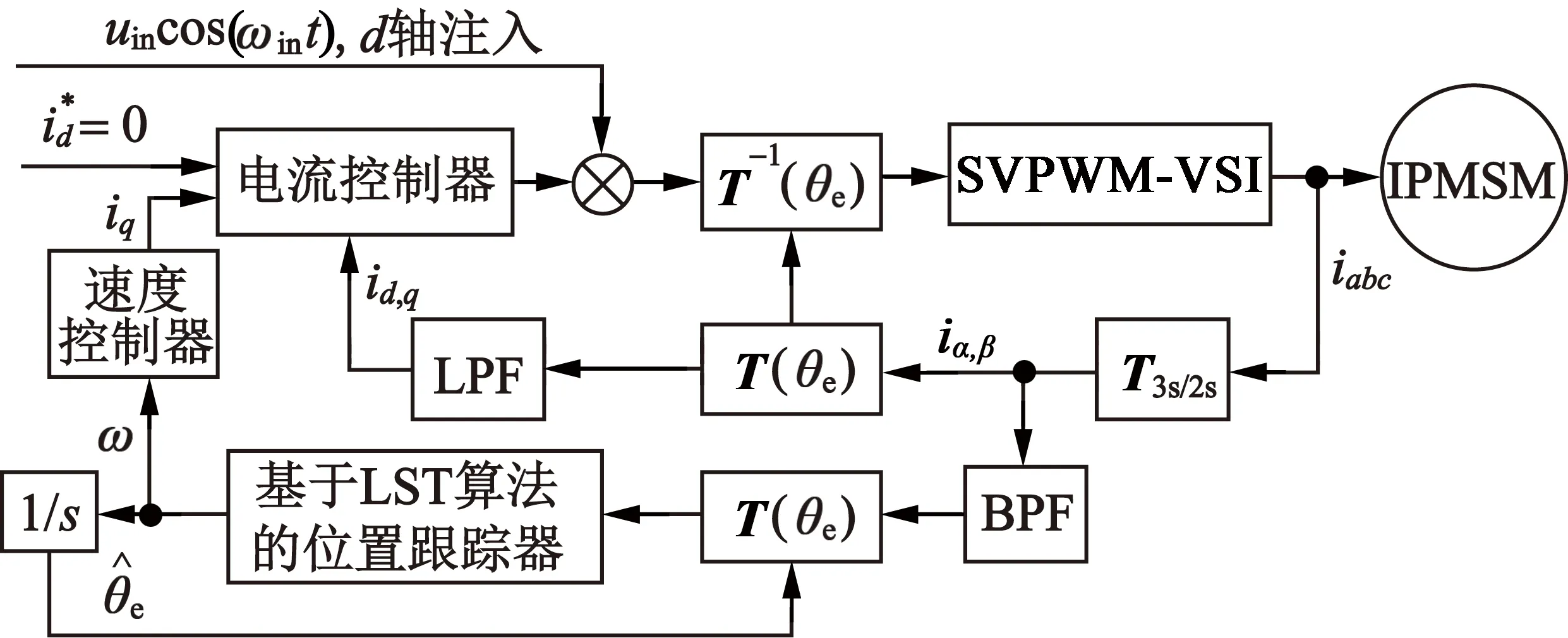
圖2 基于LST算法的脈振高頻電壓信號注入法原理框圖

為了驗證該方法的可行性，在MATLAB/Simulink環境下搭建系統仿真模型，電機仿真參數如表1所示。脈振高頻電壓信號的幅值uin=20 V，頻率ωin=1 000 Hz，低通濾波器(LPF)的設計采用巴特沃斯方法，階數為1，通帶頻率為150 Hz。帶通濾波器(BPF)的設計采用巴特沃斯方法，階數為2，低通帶邊緣頻率為987 Hz，高通帶邊緣頻率為1 018 Hz。仿真條件：采用變步長ode45算法，相對誤差為0.001，仿真時間為1 s。

表1 電機仿真參數

在參考轉速為100 r/min的空載運行下，圖3為轉子位置估計和實際值的對比圖，從圖3可以看出，估計值和實際值基本吻合。圖4為位置估計誤差，由圖4可以看出估計誤差小于1°(1 rad≈57.3°)，表明估計轉子位置能夠實時反映轉子的實際位置。

圖3 轉子位置對比圖

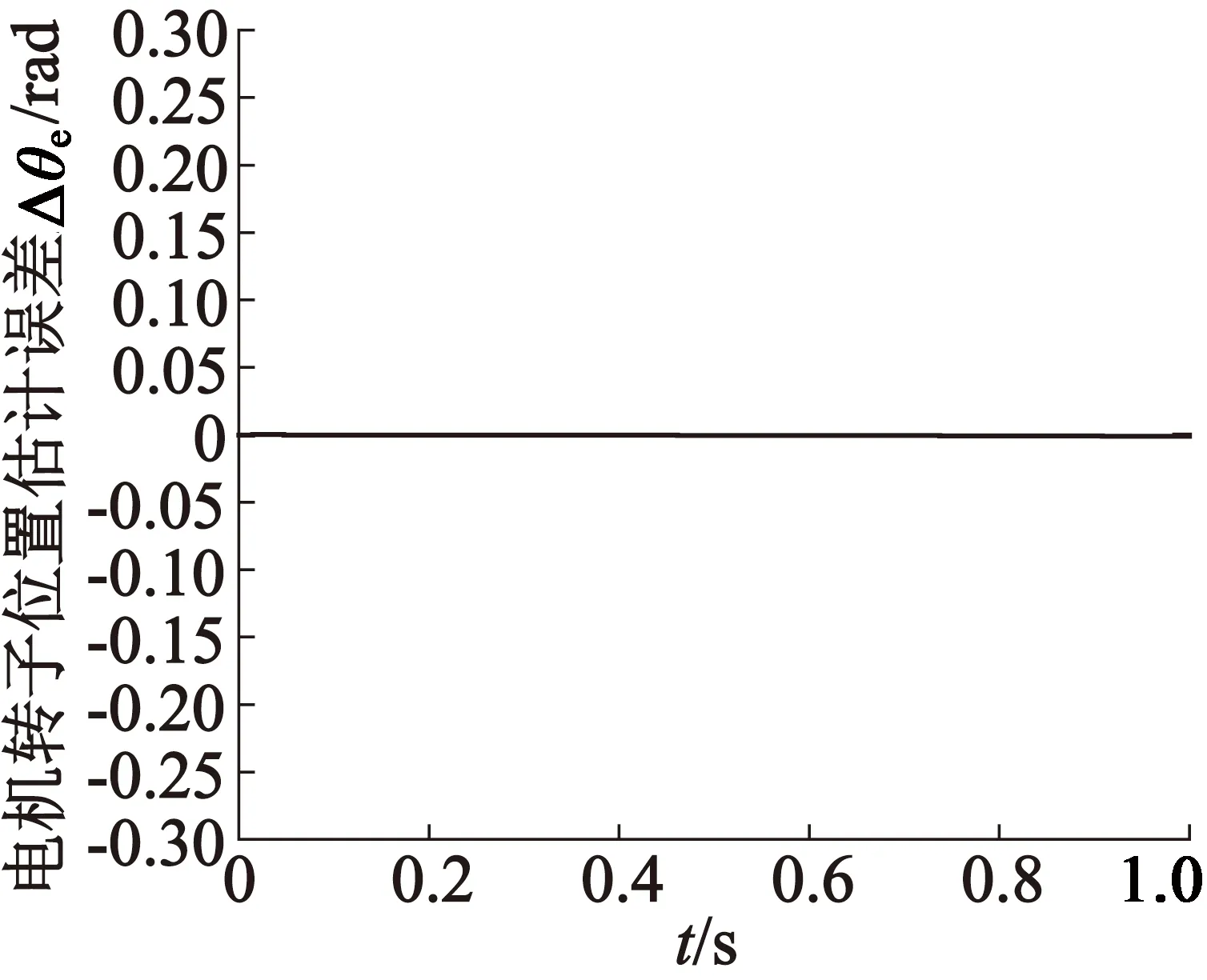
圖4 位置估計誤差

圖5為電機轉速估計值與實際值的對比圖，從圖5中可以看出，估計轉速響應速度快，超調小，較快地穩定在額定轉速值。圖6為轉速估計誤差，由圖6可以看出，在開始階段，轉速估計誤差較大，穩定之后，在轉速100 r/min時估計誤差可以控制在0.02 r/min的范圍內，說明估計轉速可以真實地反映實際轉速值，可用于電機的無位置傳感器控制。

圖5 電機轉速對比圖

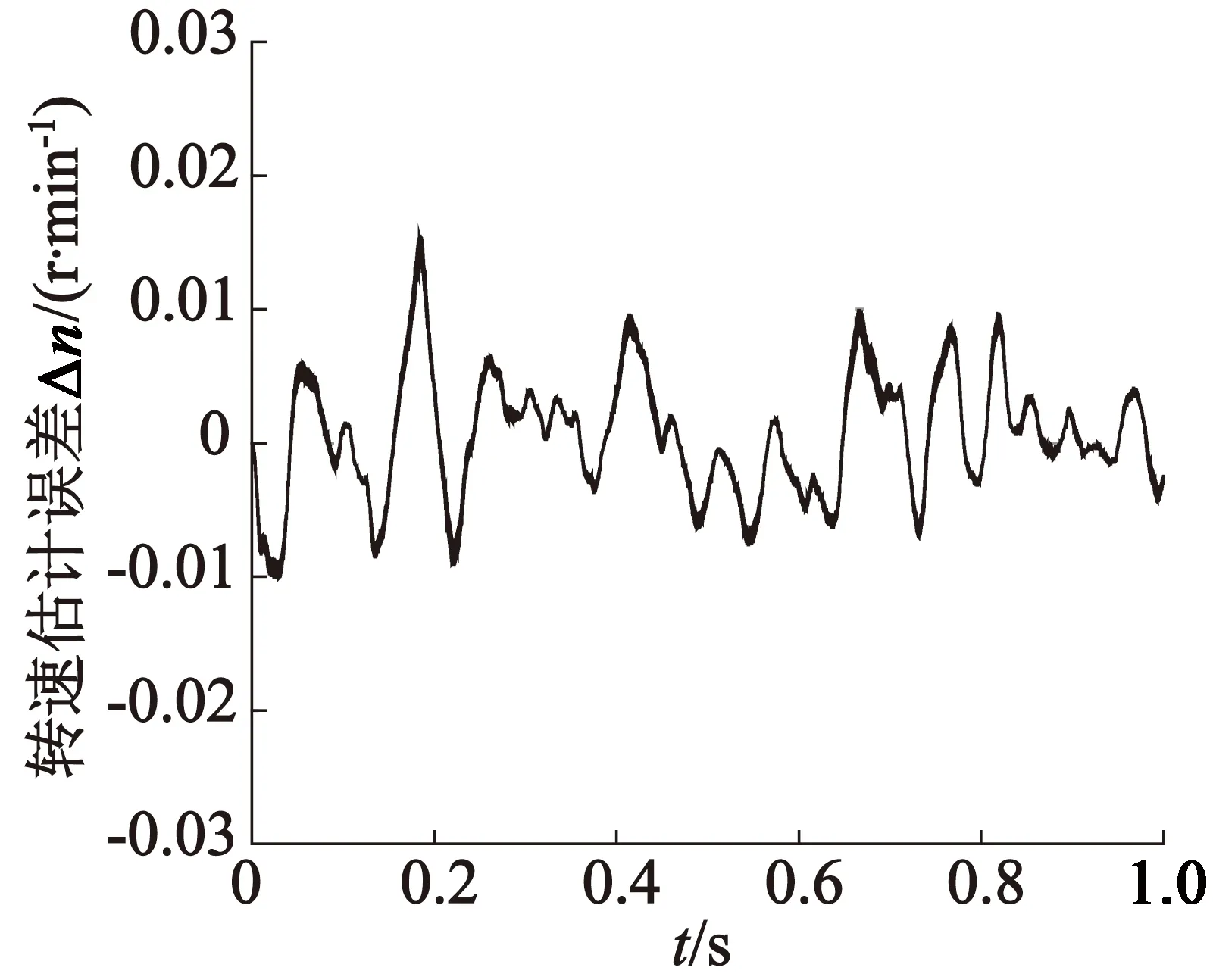
圖6 轉速估計誤差

4 結 語

本文對脈振高頻電壓信號注入法在永磁同步電機無位置傳感器控制的應用進行了研究分析，將電力系統中對電信號的分析方法——LST算法運用到電機控制系統，簡化系統結構，提高系統性能，實現了轉子誤差角度的快速準確提取，并通過仿真驗證了該方法的有效性，為永磁同步電機無位置傳感器控制提供了一種新的途徑。