永磁同步電機變指數快速冪次趨近律滑模控制

黃 燦，張遠來，李京鴻，段燕芳

(山東科技大學，青島 266590)

0 引 言

三相永磁同步電機(以下簡稱PMSM)是一個強耦合、多變量的非線性復雜系統，具有體積小、效率高、可靠性強等優點,在許多高精度控制場合被廣泛應用。目前PMSM調速大都采用PI調節器進行控制，但是當電機內部參數發生變化或者有外部擾動時，傳統的PI控制算法難以實現理想的高精度的調速要求。因此，PMSM的控制系統中應用了許多效果優異的非線性控制方法，其中包括滑模控制[1]、預測控制[2]、魯棒控制[3]、自抗擾控制[4]等。

滑模變結構控制由于其魯棒性強、對參數變化和外部擾動不敏感等優點，成為研究的熱點，并在電機控制系統中得到廣泛的應用。文獻[5]在等速趨近律中加入了系統狀態變量。該方法根據系統狀態距離平衡點的遠近，自適應調整等速趨近律的趨近速度，并減小抖振。文獻[6]采用最大轉矩電流比控制分配定子d，q軸電流，選取合適的積分滑模面和切換增益，增強了系統的魯棒性。文獻[7]通過引入非線性冪次組合fal函數，構造了基于跟蹤偏差的變速趨近律，使得切換增益具有隨系統偏差自適應調整的特性，抑制系統抖振。文獻[8]提出輸出受限約束下的變指數冪次趨近律，滿足無抖振、有限時間趨近滑模面、提高收斂速度的要求。

為了提高PMSM調速系統的動靜態性能,本文研究了一種變指數快速冪次趨近律的方法。在變指數冪次趨近律中加入純指數項和含有e-μ|s|項的函數，使系統狀態在趨近滑模面時收斂速度快，在滑模面上運動時抖振小。基于本文的趨近律，設計速度控制器，選取積分滑模面函數，在PMSM矢量系統中，與傳統指數趨近律控制、PI控制進行仿真對比，驗證變指數快速冪次趨近律速度控制器的優越性。

1 PMSM數學模型

為了方便控制器的設計，簡化分析，所選PMSM為表貼式，建立d，q坐標系下的數學模型：

(1)

式中：ud和uq分別是定子電壓的d，q軸分量；id與iq分別是定子電流的d，q軸分量；R，Ls是d，q軸坐標下的定子電阻與定子電感；p是電機磁極對數；ψf為永磁體磁鏈；TL是負載轉矩；J是轉動慣量；ωm是轉子機械角速度；B為摩擦系數[9]。

為了得到良好的控制效果，在表貼式PMSM控制系統中，令id=0。對式(1)進行整理可得如下數學模型：

(2)

設計PMSM矢量控制系統的速度控制器，就是為了讓電機在任何工況下的實際轉速ωm能快速準確地跟蹤給定轉速ω，所以定義PMSM的狀態變量：

x=ω-ωm(3)

對式(3)進行求導并結合式(2)得：

(4)

令u=iq，b=B/J，d=3pψf/(2J)，e=dω/dt，f=(Bω+TL)/J。把ω和TL的變化量當作擾動量，對式(4)進行整理，可以得到PMSM轉速控制系統狀態方程：

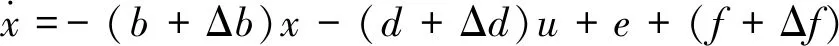
(5)

式中：Δb，Δd，Δf是電機參數變化量。令η=-Δbx-Δdu+Δf，式(5)可以簡化：

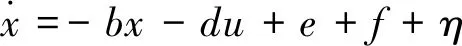
(6)

2 滑模速度控制器設計

滑模速度控制器的設計需要選擇合理的滑模面和設計合適的控制律，使系統軌跡在控制律的作用下快速趨近滑模面并沿著滑模面運動。針對PMSM轉速控制方程式(6)進行滑模面的選取與趨近律的設計。

2.1 積分滑模面的選取

傳統的滑模面函數中包含速度誤差的微分分量，容易產生高頻噪聲，引起系統抖振[10]。積分滑模面函數具有平滑轉矩、減小系統穩態誤差、削弱抖振、增強控制器穩定性的良好品質，所以本文針對PMSM轉速控制方程式(6)選取積分滑模面函數，進行速度滑模控制器的設計。積分項的s函數基本形式如下：

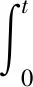
式中：k>0。

對式(7)進行求導，得到積分滑模面如下：

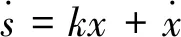
(8)

k值的大小影響系統響應趨于穩定的快慢。k值越大，穩定時間越短，但是k值太大，會加大滑模的抖振。k需要根據具體情況來選擇。

2.2 變指數快速冪次趨近律的設計

系統狀態在到達滑模面時并不是嚴格按照所設計的運動軌跡在滑模面上運動，而是在滑模面上下穿越，從而造成抖振。研究者為克服滑模控制的這一缺點，在等速趨近律、指數趨近律、冪次趨近律、一般趨近律的基礎上衍生出快速趨近律、多冪次趨近律等多種趨近律[11-13]，但大多都只是采用固定指數與固定增益的方法。本文在文獻[8]的基礎上設計了變指數快速冪次趨近律：

(9)

式中：ε>0，q>0，α>0，0<β<1，0<λ<1。

趨近律的第一部分是變指數冪次趨近項和含有指數項e-μ|s|的函數，第二項是純指數項。

1)當系統狀態遠離滑模面時，|s|的值較大，e-μ|s|趨近于零，h(s)趨近于1/λ，增大了變指數冪次項的增益，提高了趨近速度。在系統狀態接近滑模面時，e-μ|s|趨近于1，h(s)趨近于1，變指數冪次趨近項的增益保持不變，保留變指數冪次趨近項的優點。

2)當|s|≥1時，變指數快速冪次趨近律|s|的指數是|s|/α，能使系統狀態快速趨近滑模面，解決了傳統冪次趨近律趨近速度慢的問題。

3)當|s|<1時，變指數快速冪次趨近律|s|的指數是大于0小于1的常數，此時系統按照冪次趨近項和純指數項靠近滑模面，既減小了系統抖振，也增加了趨近滑模面的速度。

用經典的系統對本文所設計的趨近律與冪次趨近律、指數趨近律對比分析。考慮如下被控對象：

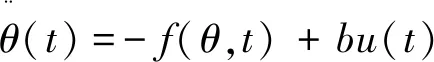
(10)

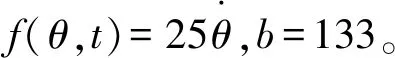
滑模函數：

(11)

式中：c>0。

跟蹤誤差：

(12)

式中：θd是理想位置信號。則：

(13)

式中：S為趨近律。

滑模控制器：

(14)

式中：c取15，指令信號θd(t)=sint。

冪次趨近律、指數趨近律、變指數快速冪次趨近律如下：

(a) 冪次趨近律

(b) 指數趨近律

(c) 變指數快速冪次趨近律

冪次趨近律、指數趨近律、變指數快速冪次趨近律仿真參數如表1所示。

表1 三種趨近律參數

三種趨近律仿真結果如圖1～圖3所示。相比指數趨近律、冪次趨近律的控制效果，變指數快速冪次趨近律無論是在趨近速度還是抑制抖振方面都有較好的優點，在趨近運動中收斂速度快，滑模運動中無抖振。

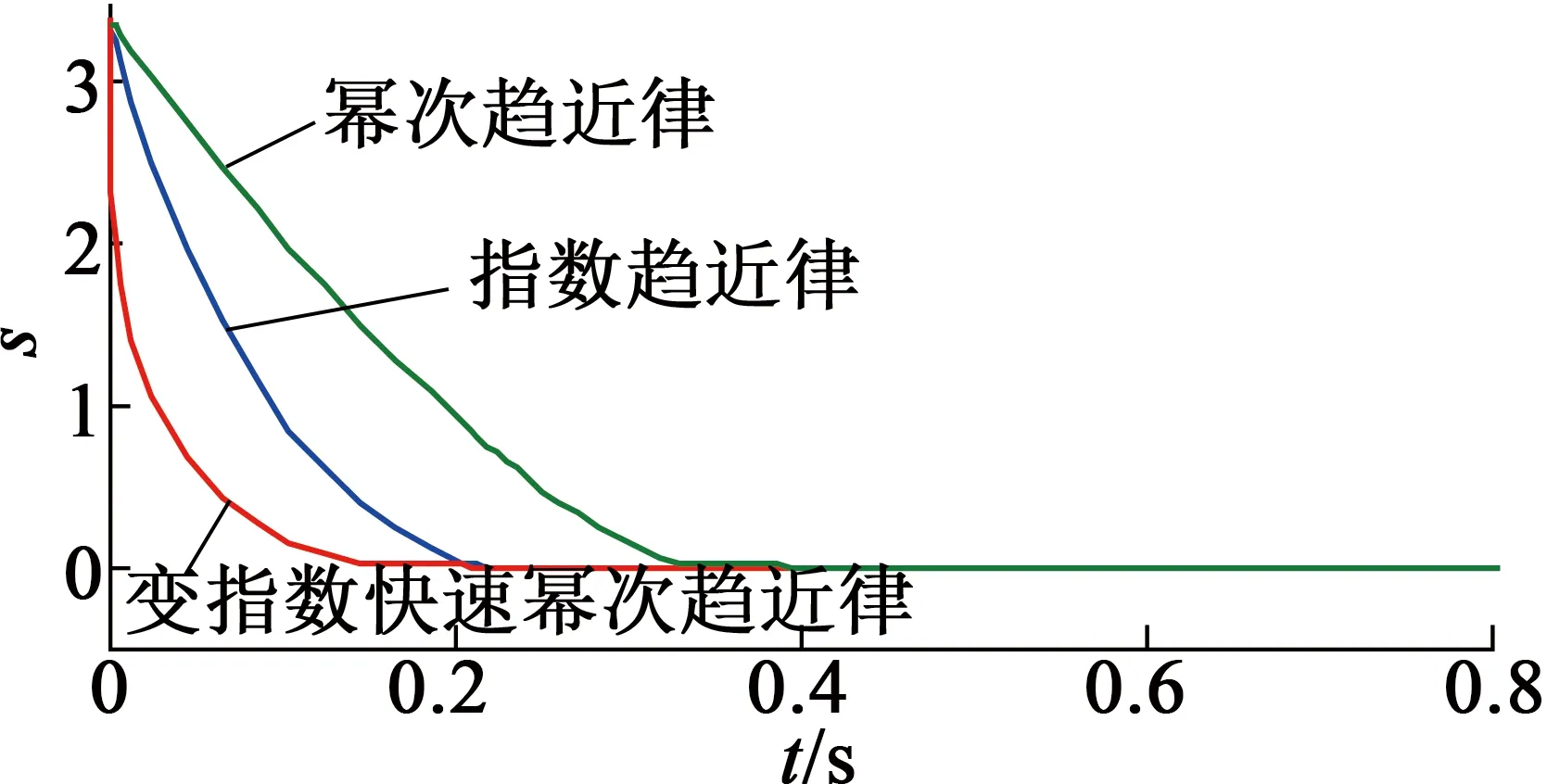
圖1滑模面函數s隨時間t變化曲線

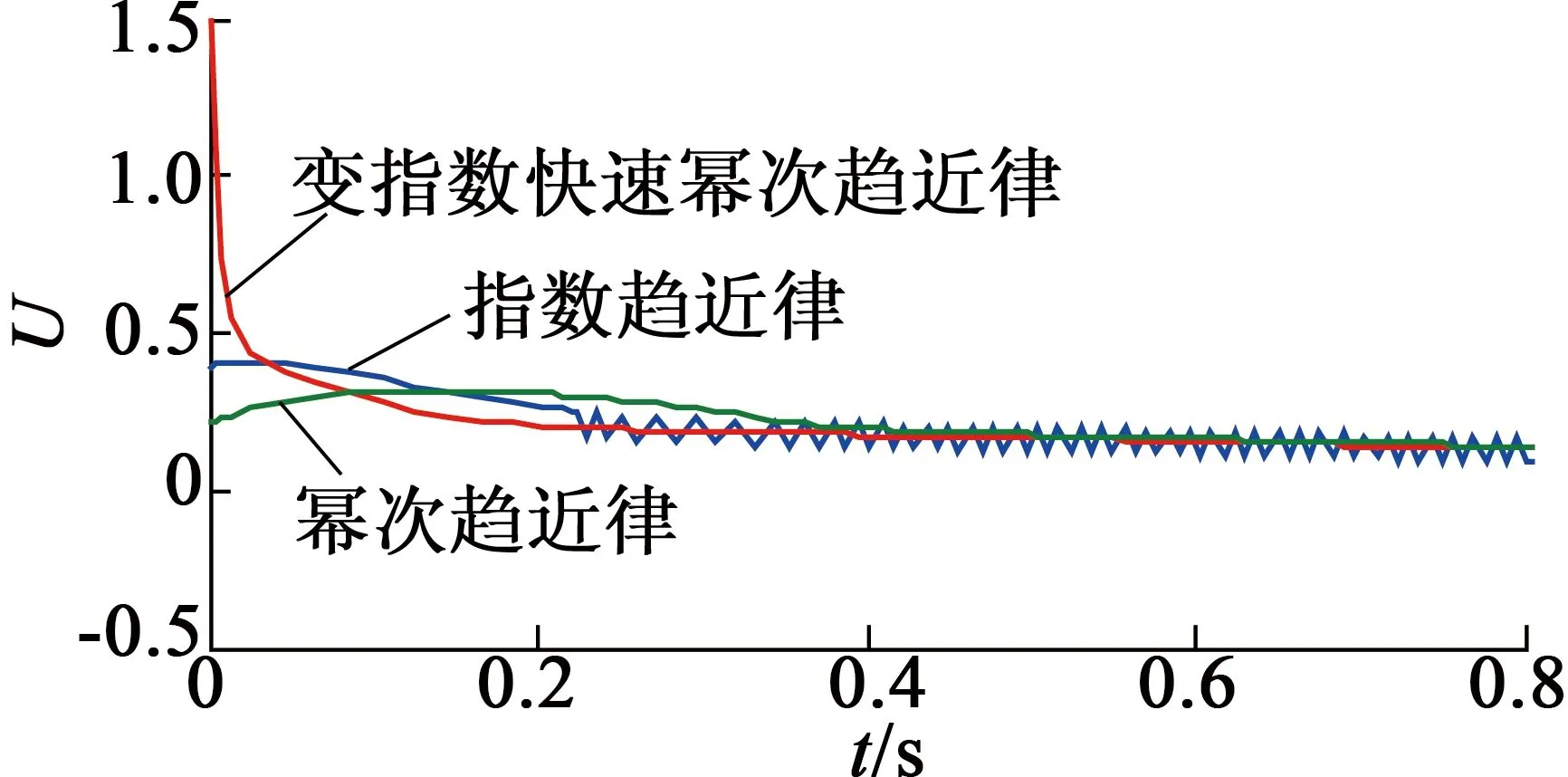
圖2控制輸入u隨t變化曲線

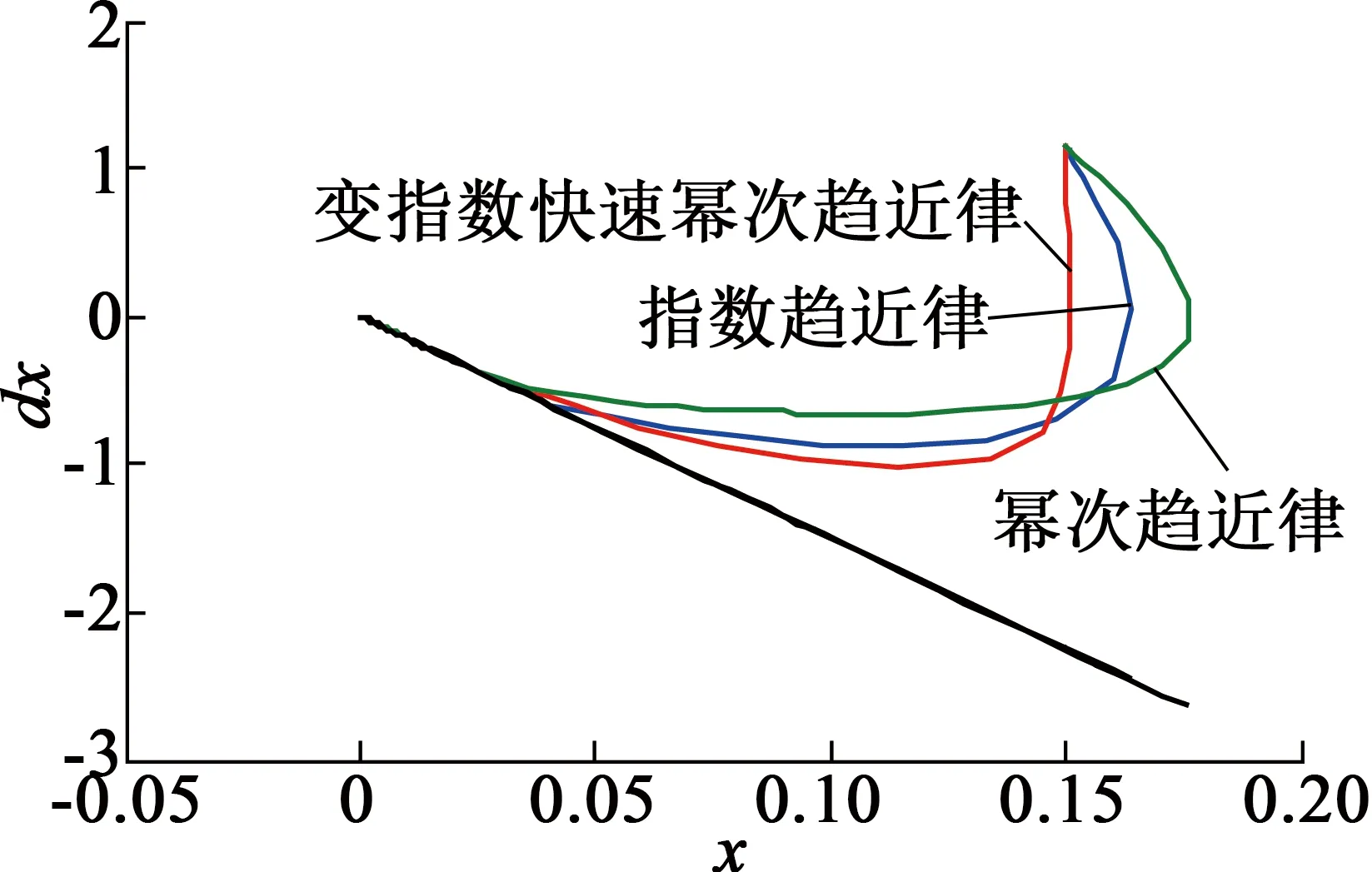
圖3不同趨近律相軌跡趨近過程

基于變指數快速冪次趨近律的優點，采用該趨近律式(9)、系統狀態方程式(6)和滑模面函數式(8)可以得到速度控制器的表達式：

(15)

3 滑模速度控制器穩定性分析

為了分析所設計的速度控制器的穩定性，首先定義Lyapunov函數：

(16)

對V(x)求導，則有：

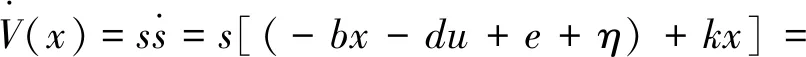
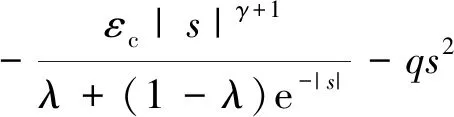
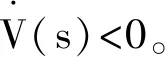
4 系統仿真及其分析

仿真對比變指數快速冪次趨近律滑模控制、指數趨近律滑模控制和PI控制。以表貼式三相PMSM矢量控制系統為例，應用MATLAB/Simulink搭建系統模型，PMSM的參數如下：極對數p=4，定子電阻R=2.875Ω，定子電感Ls=8.5mH，永磁體磁鏈ψf=0.175Wb，轉動慣量J=0.000 8kg·m2，阻尼系數B=0.001N·m·s。基于變指數快速冪次趨近律速度控制器的PMSM調速系統框圖如圖4所示，其中Nr為實際電機轉速，Nref為給定電機轉速。

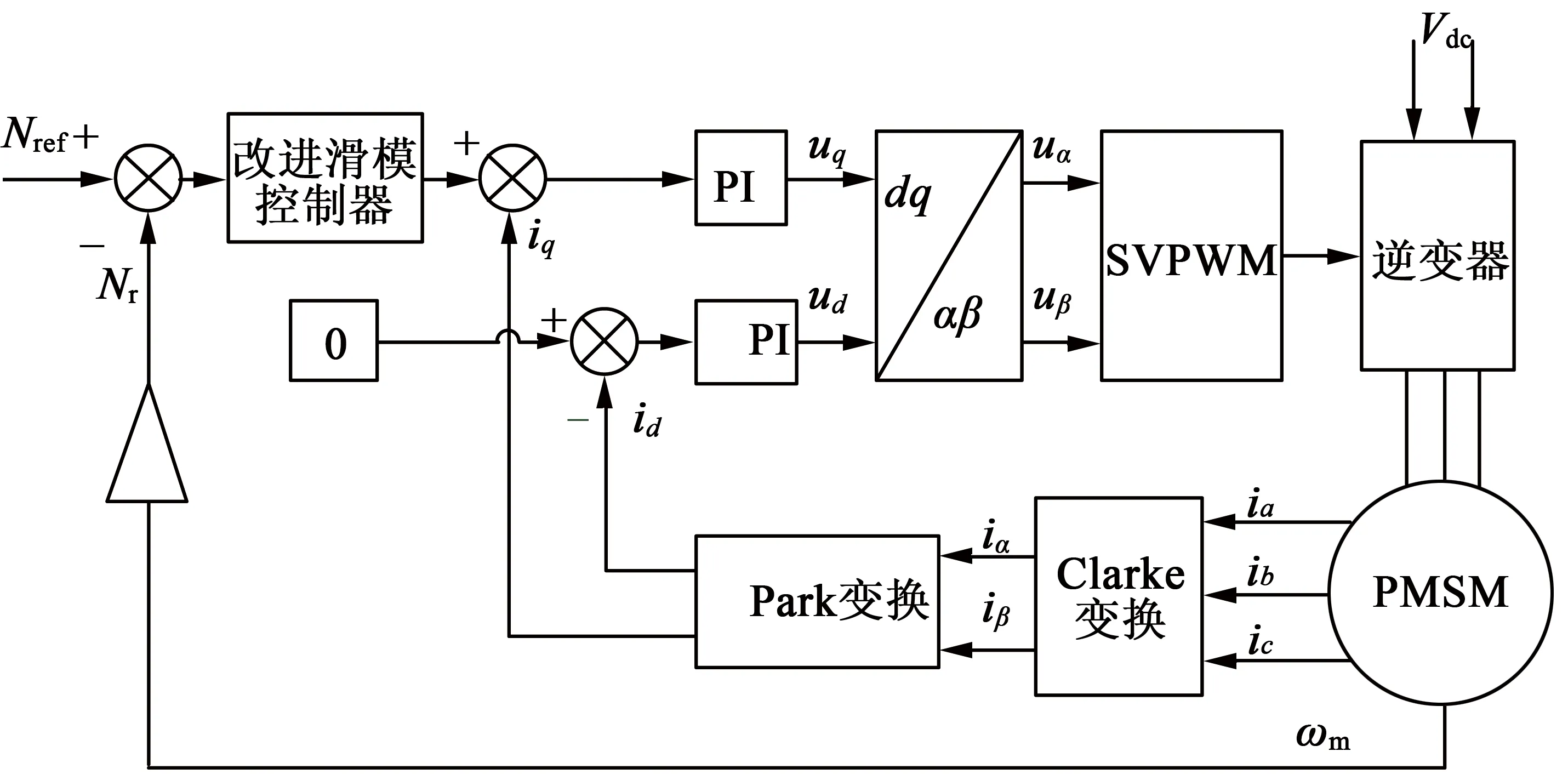
圖4基于變指數快速冪次趨近律速度控制器的PMSM調速系統框圖

上述三種控制方法的電流控制器均采用PI控制器，并且參數相同。仿真總時間為0.3s。仿真步驟如下：初始給定轉速200r/min，電機起動時負載轉矩為2N·m；在0.1s時，給定電機轉速600r/min；在0.2s時，電機負載由2N·m變為5N·m。

本文所設計的趨近律控制方法參數如下：k=2，εc=200，qc=200，α=18，β=0.5，λ=0.5；指數趨近律控制參數如下：c=55，εb=200，qb=300；PI控制器中比例增益kp=0.05,積分增益ki=0.25。

轉速響應曲線如圖5所示。從圖5(a)可知，當電機以給定速度起動時，PI控制有超調，并且響應一段時間才能恢復到給定轉速；指數趨近律控制雖然無超調，但趨近速度慢；變指數快速冪次趨近律趨近速度快，無超調。從圖5(b)可知，變指數快速冪次趨近律雖然都有一定量的超調，但是比PI控制、指數趨近律控制小得多。

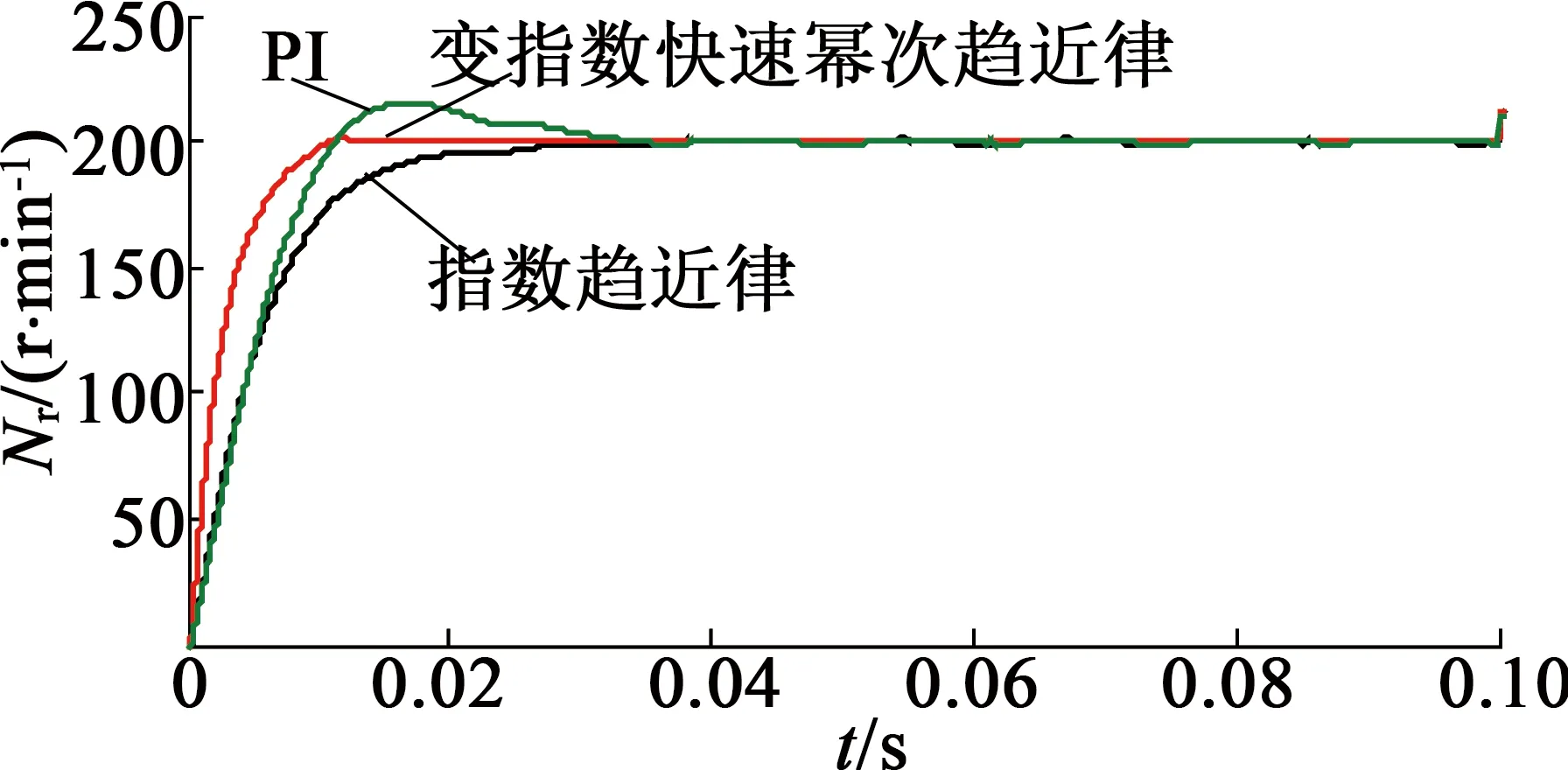
(a) 0～0.1 s轉速響應曲線

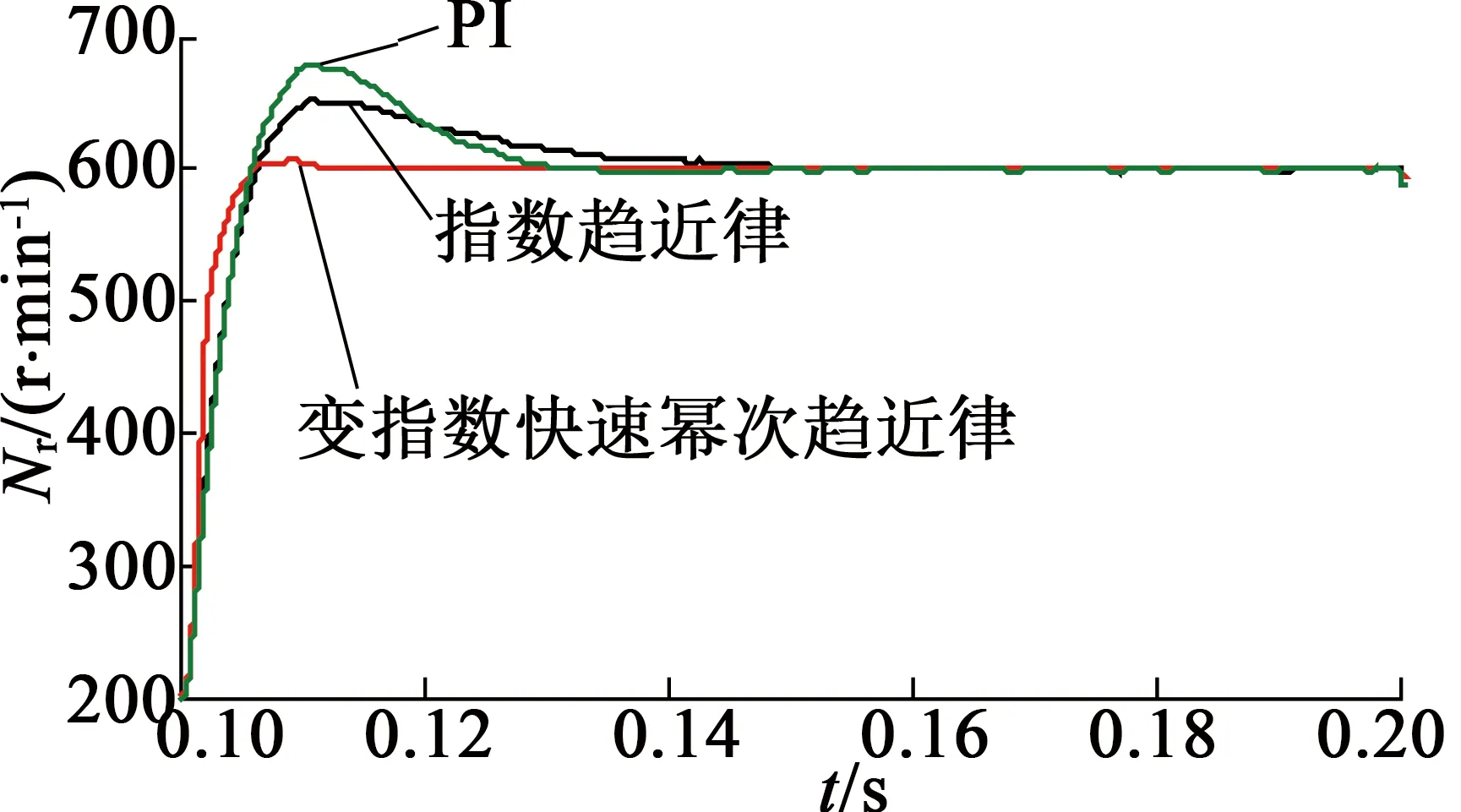
(b) 0.1～0.2 s轉速響應曲線

圖5給定速度變化時轉速響應曲線

負載轉矩變化時轉速響應曲線如圖6(a)所示，圖6(b)是0.25～0.29s轉速響應曲線放大圖。從圖6可知，變指數快速冪次趨近律控制時受擾動量小，在速度穩定時抖振小。

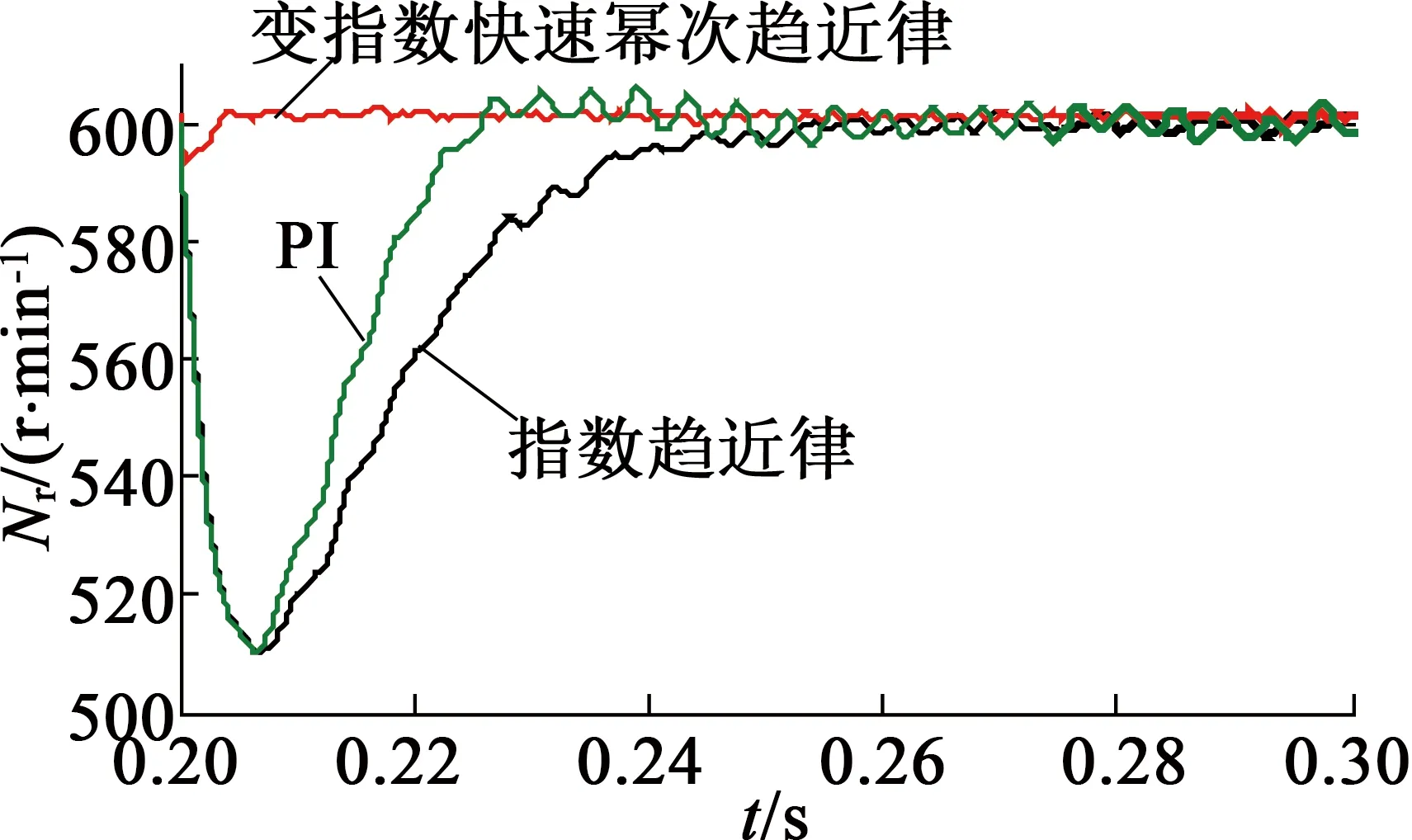
(a) 0.2～0.3 s轉速響應曲線

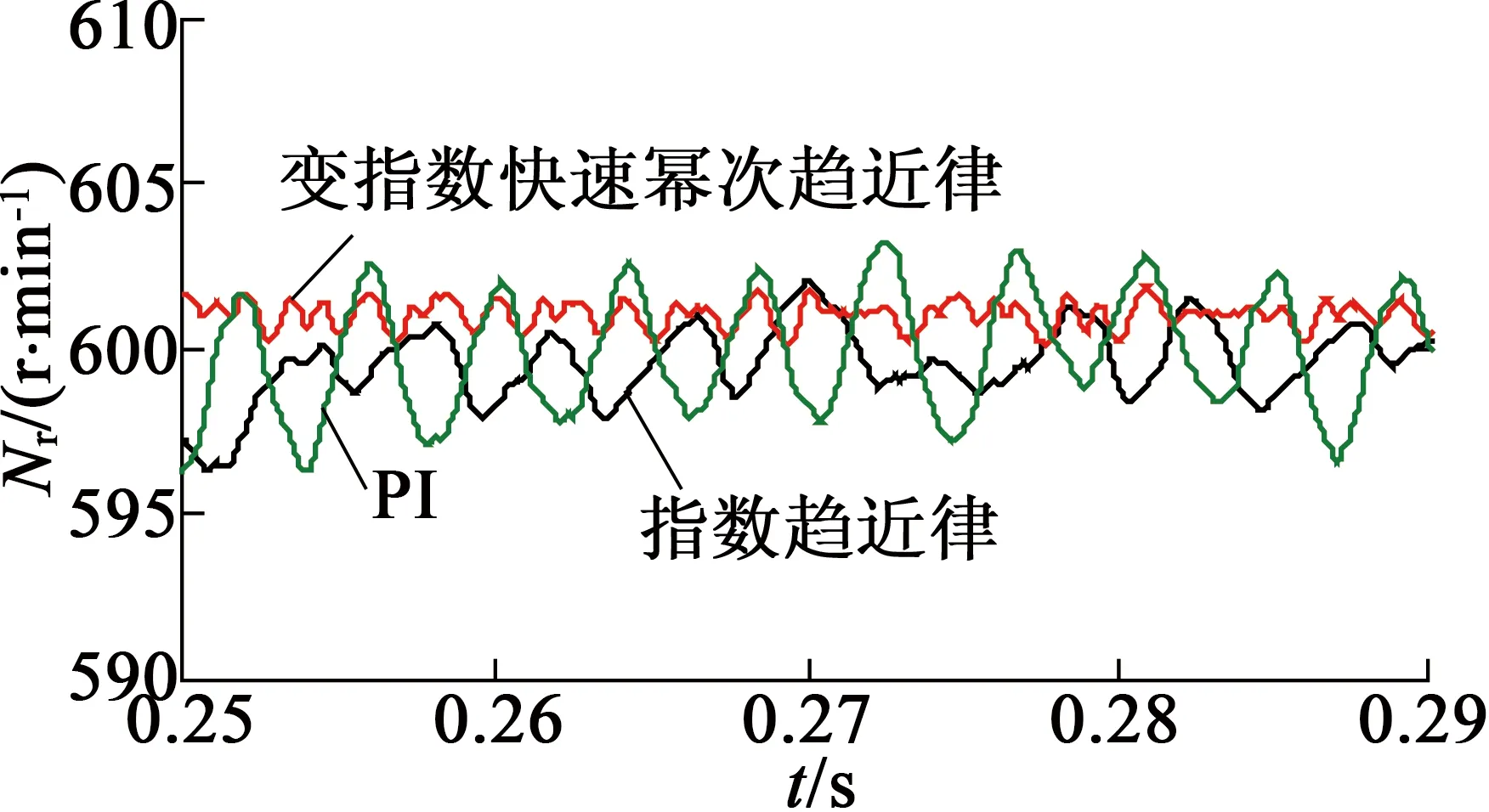
(b) 0.25～0.29 s轉速響應曲線

圖6負載變化時轉速響應曲線

為了更好地比較仿真結果，以速度響應無超調、響應時間更短為評價標準，從轉速響應曲線得到速度響應評價表，如表2所示。表2中的數據進一步說明了變指數快速冪次趨近律控制響應速度快，魯棒性強。

表2 速度響應評價表

5 結 語

針對傳統趨近律趨近速度慢，滑模變結構中固有抖振影響轉速系統性能的問題，設計了變指數快速冪次趨近律的控制方法。在變指數冪次趨近律的基礎上加入純指數項和含有e-μ|s|的函數，使系統狀態在遠離滑模面時趨近速度快，在滑模面運動時抖振小。基于變指數快速冪次趨近律，設計了積分滑模速度控制器，用Lyapunov函數證明了控制器的穩定性。在PMSM矢量控制系統中，該控制器與傳統指數趨近律控制器和PI控制器進行了仿真對比。結果表明，變指數快速冪次趨近律速度控制器在跟蹤速度、抑制抖振和消除外部負載擾動的影響等方面有較好的動靜態表現，具有較強的魯棒性和自適應性。