遼寧省水資源優化配置研究

程瑞修

(遼寧省丹東水文局，遼寧 丹東 118000)

近年來，隨著生態環境的變化和社會經濟的發展，水環境污染、水資源緊缺以及水災害頻發等問題日趨嚴峻，水資源問題已成為影響人水和諧相處以及生態文明建設的主要因素。水資源管理是以水資源配置機制為依托實現人水和諧相處的理念，是一個涉及社會水與自然水共同管理的復雜系統，通過約束和協調用水主體及水工程最終達到水資源可持續利用的目標[1]。針對水資源優化配置模型的研究國內外許多學者開展了大量的研究和探討，如王浩[2]等以黃河流域為例通過構建二元水循環系統耦合模型分析了該區域水資源配置模式，并給出了人工-天然二元水循環的結構模型。近年來，城市防洪排澇能力較低以及海綿城市的提出，不僅推動了雨洪管理模式的轉變，而且有利于城市水資源的合理調控和配置，同時促進了定量評價水資源配置問題，如李衛華[3]等以塔里木河源區為例利用投影尋蹤分類模型定量的評價分析了其水資源可持續利用水平。

目前，對水資源優化配置模型求解常用的方法主要有蟻群算法[4]、遺傳算法[5]、粒子群算法[6]等，而螢火蟲算法作為一種新的智能優化算法也被應用到水資源配置領域，并且涉及該方法的相關研究較少。據此，本文通過分析螢火蟲算法建立了優化配置模型，以期為水資源的科學配置提供了一種新的思路和解決方法。

1 螢火蟲算法

螢火蟲算法首先是由YANG于2008年提出一種可用于螢火蟲群體模擬和簡化的智能算法，每個螢火蟲在該算法中均可作為一個可行解，其亮度可代表此解的適應度[7]。螢火蟲可根據其感知能力對更亮個體進行搜尋，通過迭代作用建立相應的鄰域集，然后按照輪盤賭的方式移動，待移動完成后對其感知半徑進行更新，并進入下一輪更新亮度的迭代。通過螢火蟲的多次迭代逐漸聚集在較亮個體附近。對可變步長螢火蟲算法采用連續函數優化法基本過程如下。

(2)利用公式(1)可建立比自身亮的螢火蟲i的領域集Ni，螢火蟲i采用輪盤賭的方式向領域集Ni中j螢火蟲移動的概率pij，其表達式分別如下：

(1)

(2)

其中，螢火蟲i至領域集Ni中j螢火蟲的移動公式為：

(3)

式中，s—螢火蟲移動步長，其他各參數同上。

考慮采用可變步長的迭代方式，以此獲得更快的尋優搜尋速度，因此可采用下式對移動步長s進行調整：

(4)

式中，smax、smin—分別為移動步長的最大和最小值；gt、tmax—分別為當前和最大迭代次數。

(3)采用公式(5)、(6)分別作為螢火蟲的更新感知半徑與亮度，其表達式如下：

ri(t+1)= min{ri，max[0，ri(t)+β(ni-|Ni(t)|)]}

(5)

(6)

在當前解符合最優解或迭代至規定的次數時則停止迭代，否則重新代入進行計算。

2 建立水資源優化配置模型

2.1 目標函數

假定x為決策變量，采用下述模型作為遼寧省水資源優化配置方法，表達式如下：

(7)

式中，Z—水資源綜合效益最大值；F(x)、G(x)—分別為水資源綜合效益函數和條件約束集。

按照多個不同的子區將研究區域進行適當的劃分，其中各子區均包含多個蓄水用戶和供水水源，根據其供水范圍又可將區域內的水源劃分為獨立水源和公共水源。將研究區域劃分為K個子區，并且在k子區內存在J(k)個水用水部門和I(k)個獨立水源，在此范圍內存在M個公共水，可建立目標函數如下：

F(x)=opt[f1(x)，f2(x)，f3(x)]

(8)

式中，F(x)—水資源綜合效益函數；f1(x)、f2(x)、f3(x)—分別為社會、經濟、環境效益函數。

為便于優化模型的求解，可將式(8)中3個變量進行加權求和計算，公式如下：

(9)

采用區域內供水直接帶來的最大經濟效益代表經濟效益函數f1(x)，其表達式如下：

(10)

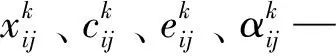
采用區域內最小的總缺水量來間接反映社會效益函數f2(x)，其表達式如下：

(11)

采用區域內最小的重要污染物排放量反映社會效益函數f3(x)，不同區域污染物排放狀況存在一定的差異，因此在選擇重要污染物時應有所區別，通常選取較為常用的汞、石油類以及氨氮類等污染物作為參數指標，假定區域內共有N種污染物，則f3(x)表達式如下：

(12)

2.2 約束條件

結合已有文獻對水資源配置模型的約束條件確定遼寧省各子區域供水、需水約束條件，采用區域發展的協調度指標，并且能夠對生態環境、社會、經濟相互協調程度進行反映[8]。區域發展程度可通過對協調度最低值的設定進行表征，其表達式如下：

(13)

其中：

(14)

(15)

(16)

2.3 綜合權重系數

對多目標問題的優化即為水資源配置的實質，確定多目標的權重系數就是對模型中不同目標的重要性進行有效的判斷。熵權法作為一種客觀權重計算方法，主要是根據指標包含的有效信息和重要性程度確定指標權重。本文對水資源多目標的權重系數考慮采用客觀與主觀相結合的方法進行確定，并成為綜合權重，求解過程如下。

(1)首先設定評價對象有m個，評價體系中包含的指標數總數為n，表達如下所示X=(xij)m×n;(i=1，2，，m;j=1，2，，n)。

(2)因不同評價指標之間的量綱和單位存在一定的差異性，為消除量綱的差異對評價結果造成的誤差需對判斷矩陣進行統一規范化處理，并得到相對隸屬矩陣：R=(rij)m×n(i=1，2，，m;n=1，2，，n)。

經濟型評價指標其計算結果越大則評價越優，經濟型評價指標的相對隸屬度可采用下式進行計算：

(17)

成本型評價指標其計算結果越小越優，此類評價指標的相對隸屬度可采用下式進行計算：

(18)

式中，rij—相對隸屬度；(xij)max、(xij)min—在不同方案中同一評價指標xij的最大值和最小值。

(3)結合評價指標熵值的具體含義，各評價指標熵的確定可按下式進行計算：

(19)

(20)

式中，Hi—評價對象中第i項評價指標的熵值；fij—第j個評價對象的第i項指標權重占評價的權重值。

根據上述計算結果可對各評價指標的熵權W求解，如下：

W=(ωi)1×m

(21)

(22)

式中，ωi—各評價指標的熵權，取值范圍為0～1，所有評價指標的熵權之和為1；W—熵權特征向量。

3 實例應用

本文以遼寧省水資源優化配置為研究對象，對目標綜合權重利用上述方法進行確定，并采用可變步長螢火蟲算法求解模型。

參考國民經濟行業分類和各行業對生態環境、社會、經濟的貢獻值確定單因子隸屬度，并利用各單因子評價結果建立相應的矩陣進行熵權、權值的計算，得到客觀權重，然后通過邀請專家對各指標的相對重要性權重進行打分，以打分平均值作為主管權重[9- 11]。利用文中所介紹的綜合權重計算方法得到相應的組合權重，結果見表1。

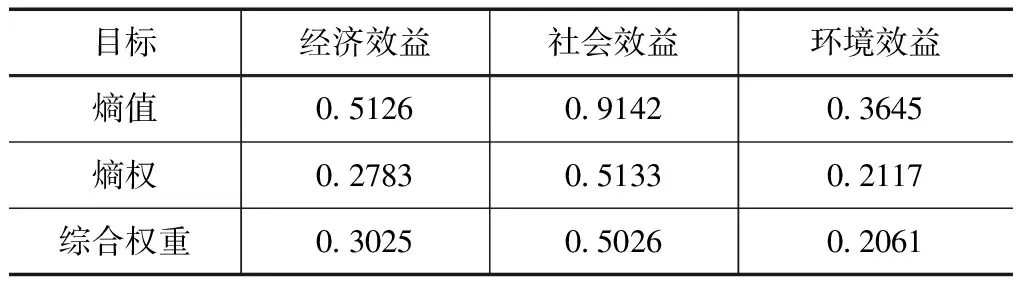
表1 多目標綜合效益值

3.1 模型參數確定

在確定模型參數時應充分考慮研究區域水資源實際狀況，部分參數參考相關文獻資料。其中螢火蟲更新因子選取為0.6，螢火蟲迭代次數為2500次，動態決策域更新率和熒光素揮發因子分別選取為0.07與0.4。

3.2 結果分析

結合遼寧省往年供水與需水量有關資料，分別對該區域2020、2025、2030年的需水量與供水量采用指標分析法進行預測。對遼寧省2020年75%保證率條件下的水資源綜合效益最優解分別利用可變步長螢火蟲算法和基本遺傳算法進行求解。結果顯示，在達到穩定最優解時，基本遺傳算法需要迭代次數為1520次，而螢火蟲算法需要1060次。由此表明，相對于基本遺傳算法，本文采用的可變步長螢火蟲法具有更快的收斂速度。

分別對50%、75%保證率下各水平年水資源優化配置模型采用螢火蟲算法進行求解，結果見表2。

表2 不同保證率下各水平年水資源優化配置

由表2計算結果可以看出，綜合效益在相同水平年隨保證率的增大呈現出一定的上升趨勢，由此進一步表明在環境、社會、經濟方面水資源優化配置呈現出更加和諧的發展趨勢。另外，不同保證率下社會效益在2020、2025、2030年均表現出增加趨勢。在實際供水量變化不大的情況下引起缺水率增加，因此為提高水資源綜合效益和利用率迫切需要進行科學調水、節約用水等措施降低對水資源的浪費，并促進社會經濟與水資源的和諧可持續發展的綜合目標[12- 13]。

4 結語

本文設定模型中螢火蟲更新因子選取為0.6，螢火蟲迭代次數為2500次，動態決策域更新率和熒光素揮發因子分別選取為0.07與0.4，結合遼寧省往年供水與需水量有關資料，分別對該區域2020、2025、2030年的需水量與供水量采用指標分析法進行預測，得出的結論如下。

(1)在達到穩定最優解時基本遺傳算法需要迭代次數為1520次，而螢火蟲算法需要1060次。由此表明，相對于基本遺傳算法，本文采用的可變步長螢火蟲法具有更快的收斂速度。

(2)綜合效益在相同水平年隨保證率的增大呈現出一定的上升趨勢，由此進一步表明在環境、社會、經濟方面水資源優化配置呈現出更加和諧的發展趨勢。

(3)在實際供水量變化不大的情況下引起缺水率增加，因此為提高水資源綜合效益和利用率就迫切需要進行科學調水、節約用水等措施降低對水資源的浪費，并促進社會經濟與水資源的和諧可持續發展的綜合目標。