非對稱單側懸臂施工斜拉橋結構參數敏感性研究

俞文龍 朱 飛 張勝雷

（1.中鐵十七局集團有限公司 山西太原 030006；2.中鐵十七局集團上海軌道交通工程有限公司 上海 200135）

1 引言

施工監控是保證橋梁實現設計意圖并確保施工安全的重要途徑［1-2］。在斜拉橋施工中，施工工序較多、施工程序復雜，結構影響參數也較多［3-4］。設計階段，這些結構影響參數多按規范或理論計算進行取值，但在實際施工過程中由于實際控制水平以及人為、材料等因素的影響，參數實測值與規范、理論值之間會存在一定的偏差［5］。此偏差將會引起橋梁結構實際受力狀態與設計狀態之間的差異。因此有必要對結構影響參數進行分析，找出敏感性參數。對于敏感性參數則需要通過正確地識別和修正，減小計算值與實際值之間的偏差；對于非敏感性參數，修正的范圍可適當放寬。敏感參數的合理取值與修正，不僅關系到橋梁的順利合龍，也關系到成橋的內力狀態和成橋線形，更關系到橋梁的施工安全［6-7］。

同時，斜拉橋施工方法的不同也將影響成橋時的結構內力以及主梁線形［8］。目前常規的混凝土斜拉橋施工方法是掛籃對稱懸臂澆筑，而本文研究的背景工程斜拉橋為非對稱結構，主跨側施工為掛籃懸臂澆筑，而邊跨側為支架現澆。對本橋梁結構進行參數敏感性分析，目的就是為了確定出對橋梁施工及結構受力影響較大的幾個主要參數，據此為橋梁施工監控提供理論依據［9］。

2 工程概況

蘇州長滸大橋CA輔道橋為非對稱、單塔單索面預應力混凝土斜拉橋，主橋跨徑布置為104 m＋75 m，主橋全長179 m，標準橋寬19 m。主橋采用剛構體系，墩塔梁固接。斜拉索采用扇形索面，梁上標準索距為7 m，邊跨加密段為3.5 m；塔上索距為1.8 m，全橋共24對斜拉索。主梁為單箱雙室斜腹板箱梁截面，中心線處梁高2.1 m，頂板寬19 m，底板寬8 m，翼緣板懸臂長度為3.5 m，箱梁頂板設1.5%的單向橫坡，底板水平。橋梁0#段長28 m，采用支架法現澆。跨運河側主跨采用前支點復合式牽索掛籃懸澆，分為標準節段、合龍段和支架現澆段，其中掛籃澆筑標準段每節長度為7 m，共11節段，編號分別為1#～11#節段，主跨現澆段長11 m，主跨合龍段長2 m。邊跨采用支架法現澆，與主梁0#段同步澆筑完成。由于斜拉橋設計為非對稱結構，為保證斜拉索拉力均衡以使主塔不承受過大的水平荷載，設計在邊跨側設有永久填充鐵塊。填充鐵塊布置在邊跨5#斜拉索向外的箱室內，除最外側兩節箱室，各節箱室填充鐵塊荷載重94.5 t，最外側兩節箱室填充鐵塊荷載分別為98 t和110.3 t。具體橋梁布置及節段劃分如圖1所示。

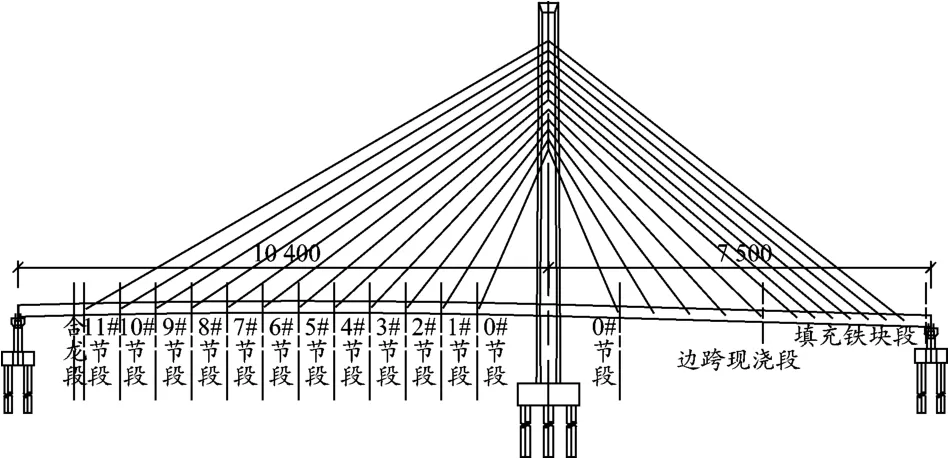
圖1 長滸大橋主橋總體布置（單位：cm）

3 結構影響參數分析

橋梁結構影響參數分析就是要確定出對橋梁施工及受力影響較大的設計參數，此參數即為敏感參數，影響相對較小的為非敏感參數［10］。而如何判斷各參數對橋梁受力狀態的影響，需要確定具體控制目標。對于斜拉橋，最主要的目標狀態就是成橋狀態和最大懸臂狀態。成橋狀態為橋梁施工的最終狀態，是施工過程控制的目的，控制好此狀態即可順利地完成設計意圖；最大懸臂狀態往往是橋梁施工過程中受力最不利的狀態，控制好此狀態，基本可以保證橋梁施工安全。因此本文分析各參數敏感性時確定的控制目標為：

（1）成橋狀態：成橋主梁線形、成橋主梁頂底面應力和成橋索力。

（2）最大懸臂狀態：最大懸臂端豎向位移、主梁根部頂底面應力。

根據背景工程橋梁的具體特點，擬分析的橋梁設計參數包括：主梁混凝土容重、混凝土彈性模量、斜拉索彈性模量、斜拉索初張力、主梁預應力荷載、施工臨時荷載以及邊跨填充鐵塊荷載。

3.1 參數敏感性分析

參數敏感性分析可采用的方法為：將擬分析的設計參數增大一定的幅值（此處取增大10%），其他設計參數不變，將成橋主梁線形、成橋主梁頂底面應力和成橋索力作為控制目標。對不同設計參數進行分別計算，根據計算所得的控制目標值隨設計參數變化的程度可以確定出敏感參數。

計算得出成橋狀態各控制目標隨各設計參數的變化如圖2～圖5所示。圖中橫坐標X表示主梁縱向里程，以主塔位置為坐標零點，主跨側為負里程，邊跨側為正里程；橫坐標索編號正值代表邊跨側斜拉索編號，負值代表主跨側斜拉索編號。

根據各計算結果分析得出：對成橋主梁線形影響較大的設計參數分別為斜拉索初拉力、主梁混凝土容重和斜拉索彈性模量，而其他幾個設計參數對主梁成橋線形影響相對較小；對于成橋索力影響較大的設計參數分別為主梁混凝土容重、斜拉索初拉力、鐵塊荷載和預應力荷載，其他幾個設計參數對成橋索力影響較小；對于成橋主梁頂底面應力，影響較大的參數分別為斜拉索初拉力、主梁混凝土容重、主梁預應力荷載和施工臨時荷載，其他參數對主梁成橋頂底面應力影響相對較小。綜合判斷，斜拉索初拉力和主梁混凝土容重對成橋狀態的幾個控制目標都有較大的影響，可確定為敏感參數；其余參數或是對某個控制目標影響較大，或是對各控制目標影響都相對較小，可判斷為非敏感參數。

圖2 設計參數增加10%引起的主梁豎向位移變化曲線

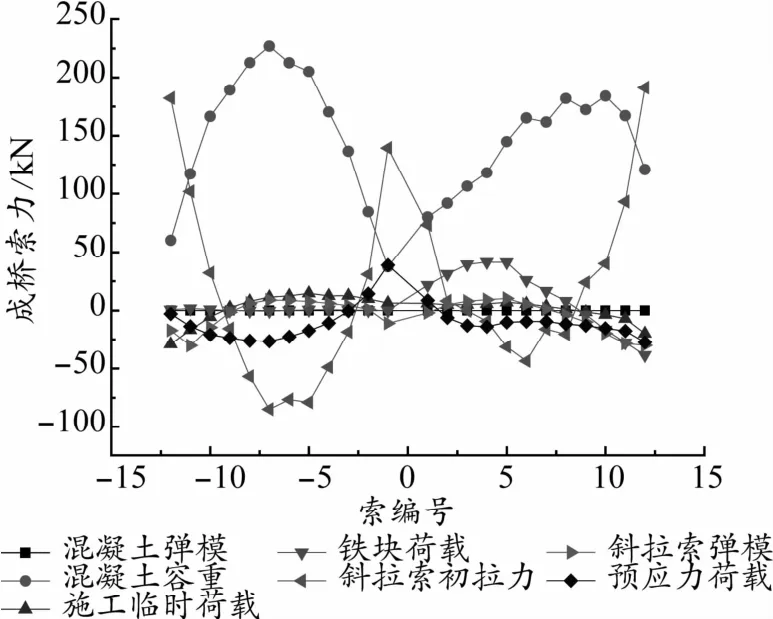
圖3 設計參數增加10%引起的成橋索力變化曲線

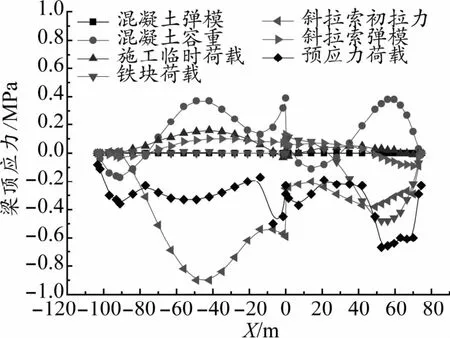
圖4 設計參數增加10%引起的主梁頂面應力變化曲線

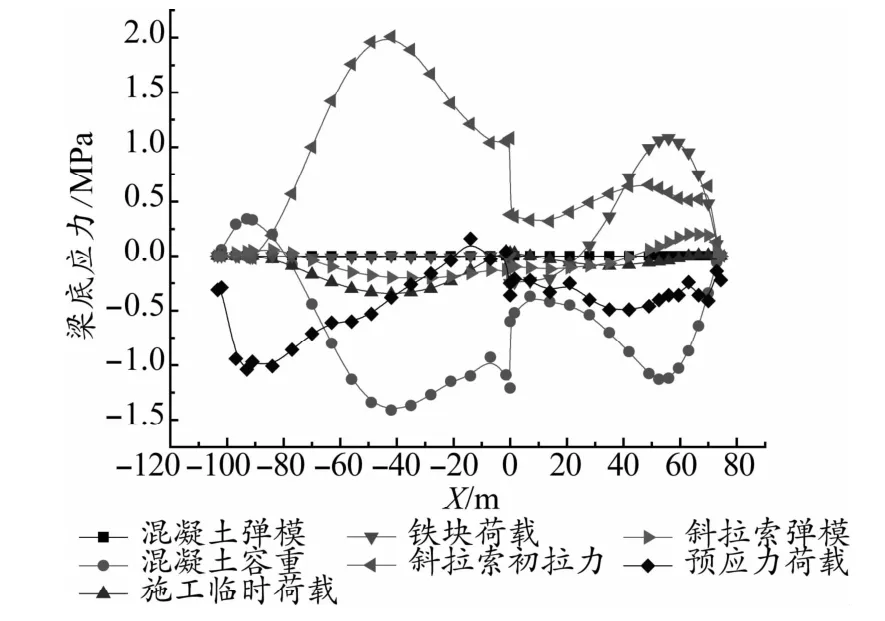
圖5 設計參數增加10%引起的主梁底面應力變化曲線

3.2 敏感度計算

以上分析方法可直觀地對比出各參數對控制目標的影響程度大小，并初步判斷出敏感參數和非敏感參數，但對控制目標的影響程度沒有給出量化指標。為更好地判斷各參數變化對控制目標影響的敏感性，以參數敏感度為具體指標［11］，對比分析設計參數敏感性。

參數敏感度計算原理為：僅對某一設計參數進行數值調整，其他設計參數不變，借以考量該設計參數的相對影響因子［12］。具體分析方法為：將最大懸臂狀態主梁懸臂端豎向位移和主梁根部頂底面應力作為控制目標，將各設計參數分別調整-6%、-3%、0、＋3%、＋6%，計算出不同調整率下的控制目標值。參數調整率與控制目標變化值之間的關系如圖6～圖8所示。從圖中可以看出控制目標變化值與參數調整率之間基本都呈線性關系，控制目標變化值與參數調整率組成的關系曲線斜率即可被定義為相應控制目標隨對應參數變化的敏感度。此敏感度的大小直接反映出設計參數變化對控制目標的影響程度，敏感度數值越大表示參數變化對控制目標的影響越大，敏感度值為正表示控制目標與設計參數之間呈正比例變化關系，敏感度值為負表示控制目標與設計參數之間呈反比例變化關系。根據以上計算方法，計算得出不同設計參數相對于控制目標的敏感度數值如表1所示。

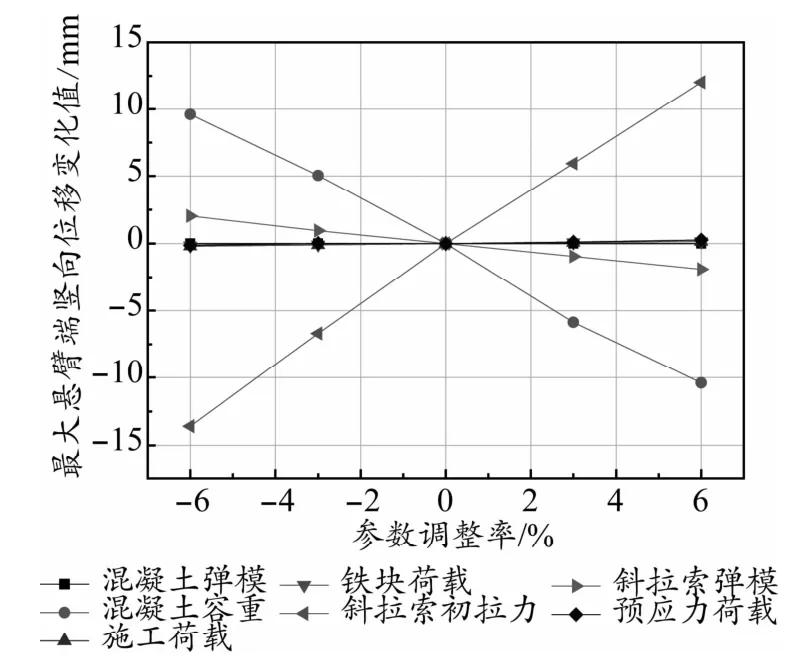
圖6 最大懸臂端撓度與各參數調整率關系曲線

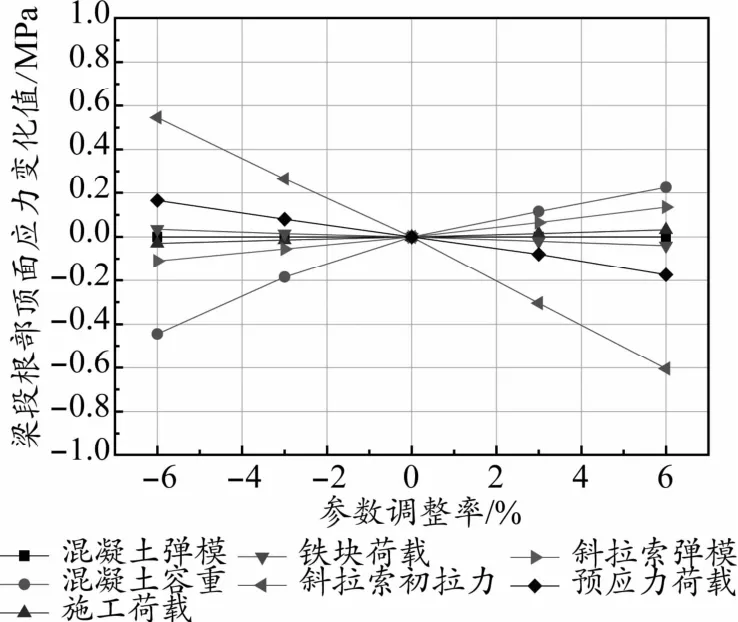
圖7 梁段根部頂面應力與各參數調整率關系曲線

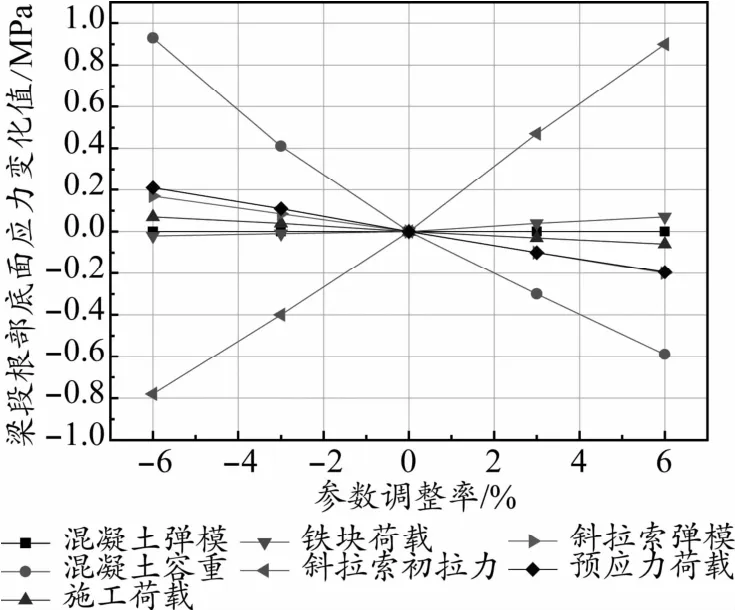
圖8 梁段根部底面應力與各參數調整率關系曲線

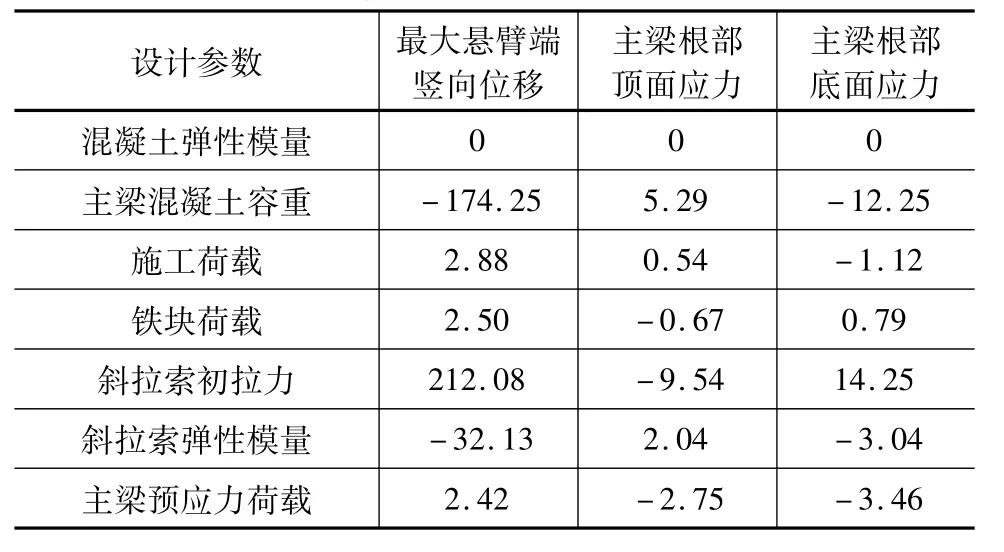
表1 不同設計參數相對于控制目標的敏感度值

從表1計算得出的敏感度值可以判斷，本橋最大懸臂施工狀態工況下，對主梁懸臂端豎向位移影響較大的設計參數依次為斜拉索初拉力、主梁混凝土容重和斜拉索彈模，此三個參數可判斷為主梁懸臂端豎向位移敏感參數，其余參數對主梁懸臂端豎向位移影響敏感度值較小，可判定為非敏感參數。對于主梁根部頂面應力影響較大的設計參數依次為斜拉索初拉力和主梁混凝土容重，此兩個參數可判斷為主梁根部頂面應力的敏感參數，其余參數可判定為主梁根部頂面應力的非敏感參數。對于主梁根部底面應力影響較大的設計參數依次為斜拉索初拉力、主梁混凝土容重、主梁預應力荷載和斜拉索彈模，此四個參數可判斷為主梁根部底面應力的敏感參數，其余參數可判定為主梁根部底面應力的非敏感參數。

綜合以上三個不同控制目標的不同參數敏感度數值，可認為對本斜拉橋最大懸臂狀態影響較大的設計參數為斜拉索初拉力和主梁混凝土容重，其余參數或是對某些控制目標影響稍大，或是對所有控制目標影響都較小，可判斷為非敏感參數。

4 結論

（1）以成橋狀態主梁線形、主梁頂底面應力以及成橋索力為控制目標，將各結構影響參數增大10%的幅值，得出敏感參數為斜拉索初拉力和主梁混凝土容重，其余參數可確定為非敏感參數。

（2）以最大懸臂狀態最大懸臂端豎向變形和主梁根部頂底面應力為控制目標，以參數敏感度為指標，分析得出此狀態下敏感參數為斜拉索初拉力和主梁混凝土容重，其余參數可判斷為非敏感參數。

（3）以成橋狀態和最大懸臂狀態分析得出的橋梁敏感性參數結論基本一致，以參數敏感度為指標可以量化判斷參數敏感性，建議具體分析時采用此類方法。