藍印花布紋樣建模與重構

陶 晨， 段亞峰， 徐蓉蓉， 楊劍平， 周 赳

(1. 紹興文理學院 紡織服裝學院， 浙江 紹興 312000； 2. 浙江理工大學 材料與紡織學院、絲綢學院， 浙江 杭州 310018)

作為國家非物質文化遺產之一，中國藍印花布是具有濃郁民族特色的紡織品。由于傳統工藝的特點，藍印花布紋樣總是以或斷或續的點和短線構成[1]，其獨特的藝術形式深刻地反映出中國傳統思想和美學觀念。已有大量文獻探討傳統藍印花布紋樣的文化與藝術內涵，但對于藍印花布紋樣的創新或未來則鮮有涉及。盡管可以提取紋樣元素，利用某些平面設計軟件進行再組合[2]，但這并不體現設計方法或模型。在紡織紋樣生成技術方面，已有的研究方法主要是依靠一些數學模型的可視化，典型的研究，如利用Mandelbrot 集變換的印花圖案設計[3]、L系統用于針織花型的設計[4]、弱混沌系統用于噴墨印花圖案的設計[5]等。此類方法得到的紋樣雖造型獨特；但具有很大的隨機性，難以保留原紋樣的特征，因此并不適用于藍印花布紋樣或其他經典紋樣的創新設計。

本文研究探索藍印花布紋樣的數學模型，使用數學模型進行紋樣的匹配和重構，實現紋樣的參數化，對參數化的紋樣進行函數映射和骨架重組，達到紋樣改造和創新設計的目的。本文提出的藍印花布紋樣的建模、重構和改造方法，可在保留藍印花布紋樣關鍵特征的同時，為藍印花布紋樣注入新的活力，以期在傳統紋樣的傳承和創新中發揮積極作用。

1 研究方法

本文研究所使用的紋樣來自一個藍印花布紋樣庫[6]，包含各種經典藍印花布紋樣，可作為中國傳統藍印花布紋樣的代表。典型紋樣(局部)如圖1所示。

圖1 藍印花布紋樣示例Fig.1 Sample of blue calico pattern

傳統工藝的特點決定了藍印花布紋樣在基本元素構成上，總是以各種形態的分離的點或短線呈現，通過點的大小、形態與疏密的變化達到紋樣造型的多樣性。此外，如受中國傳統哲學中關于陰陽平衡的影響，傳統藍印花布紋樣在基本元素構形上講求“剛柔并用”“凹凸互補”，通過對立統一達到和諧的效果，因此，建模的重要目標，除了表達紋樣元素豐富多樣的形狀，還要實現在剛與柔、凹與凸之間自由調節的能力。

1.1 模 型

1.1.1張力系數

給定4個控制點P0,P1,P2,P3，基數樣條C由以下公式[7]確定：

C=m1h3(a)+P1h1(a)+P2h2(a)+m2h4(a)

(1)

式中：a為插值參數；h1,h2,h3,h4為經典三次Hermite多項式，分別為：

(2)

基數樣條曲線以P1,P2為端點；m1,m2分別為曲線在點P1,P2處的正切值。

(3)

t即為張力系數，0≤t≤3。由式(3)可知：曲線在P1處的斜率由P0,P2,t決定；在P2處的斜率由P1,P3,t決定。圖2示出張力系數對曲線外觀的影響。

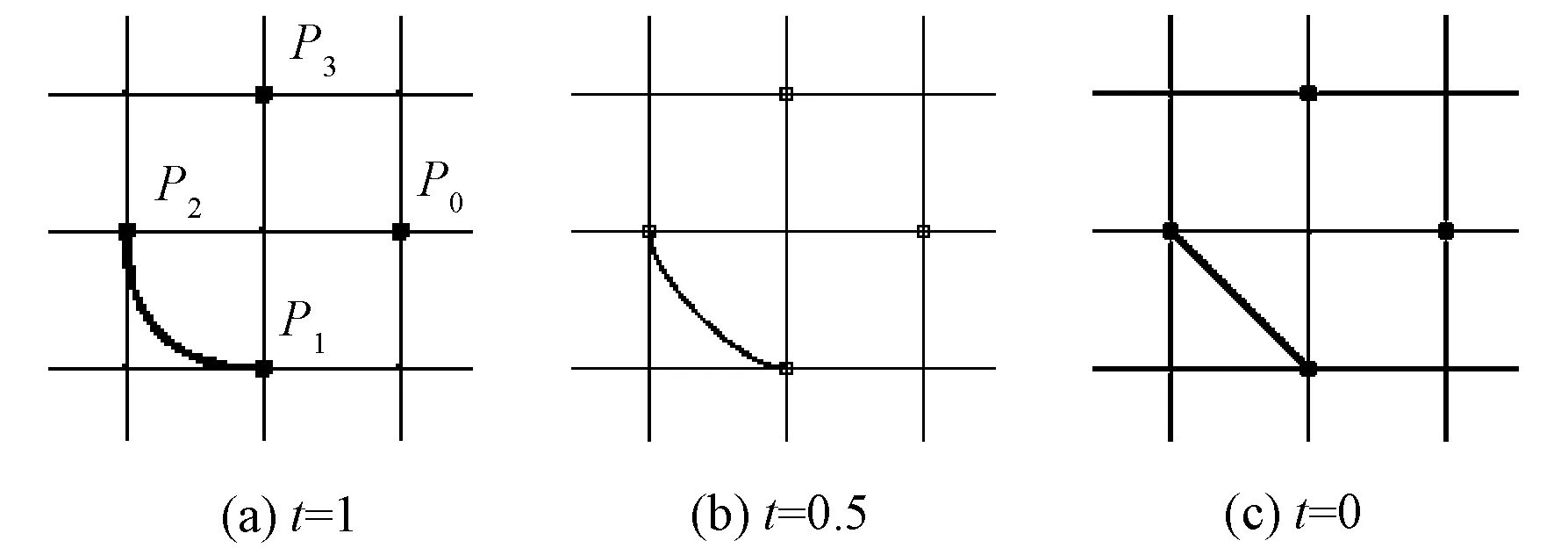
圖2 張力系數對樣條曲線的影響Fig.2 Influence of tension coefficient on spline

可見，利用張力系數能夠實現樣條曲線剛柔性的調節：張力系數值越大，曲線越柔和；反之則越剛硬；當t=0時，樣條退化為直線。為得到封閉的形狀，需將若干條樣條曲線首尾相接。對于P0,P1,P2,P34個節點的情況，可由如下順序確定4條基數樣條曲線：(P0,P1,P2,P3)、(P1,P2,P3,P0)、(P2,P3,P0,P1)、(P3,P0,P1,P2)，如圖3所示。

圖3 由基數樣條構成的封閉圖形Fig.3 Closed figuires composed of cardinal splines

這4條曲線首尾相連構成封閉形狀，且由基數樣條的關于端點處斜率的性質可知，在每個節點處連接平滑。通過調整張力系數，圖3中圖形實現了從圓紋到方紋的轉變。

1.1.2節點配置

將圖3所示圖形置于直角坐標系中，并進一步規定：P0,P1為活動節點，P2,P3為固定節點，如圖4所示。P2,P3位于坐標軸上，其坐標分別為(-1,0)和(0,1)。活動節點P0,P1則可在一定范圍內偏離坐標軸，其具體位置由活動半徑(r0,r1)和偏離角(d0,d1)決定。由此構成的圖形作為紋樣元素的一般模型。

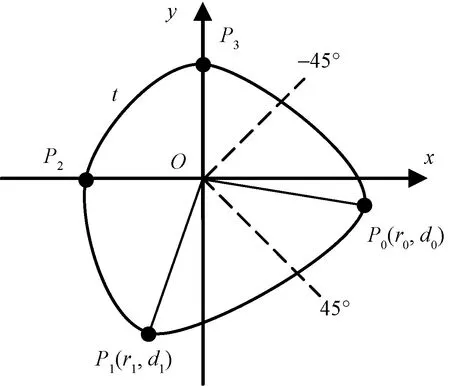
圖4 元素模型Fig.4 Element model

該模型具有t,r0,d0,r1,d1共5個構形參數，其中t為樣條曲線的張力系數。各個參數的取值范圍規定如下：

(4)

對活動半徑r0,r1取值范圍的限制是為了避免出現長條形實例(藍印花布紋樣元素應當避免的形狀)。對偏移角d0,d1(順時針為正，逆時針為負)取值范圍的限定，是為了將2個活動節點控制在各自的活動空間內，防止因交錯導致形狀畸變。張力系數t的取值范圍由基數樣條的性質決定。當這些參數值確定，模型形狀即確定。由特定構形參數值確定的模型形狀稱為模型實例。模型實例經仿射變換(平移、縮放和旋轉)即可匹配藍印花布紋樣中的元素形狀，如圖5所示。可見該模型對傳統藍印花布紋樣中一些典型元素的表達能力。

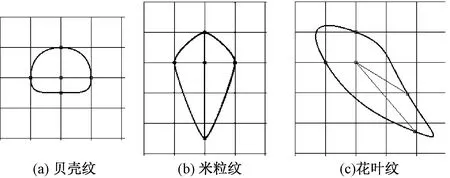
圖5 由模型實例表達的紋樣元素Fig.5 Pattern elements expressed in model instances.(a)Shell; (b)Rice; (c)Petal

圖5(a)所示為貝殼紋，模型參數為t=1.05,r0=1,d0=0,r1=0.5,d1=0；圖5(b)所示為米粒紋，模型參數為t=0.3,r0=1,d0=0,r1=2.5,d1=0；圖5(c)所示為花葉紋，模型參數為t=1.2,r0=2,d0=31.5,r1=3,d1=-40.5。實驗結果表明，該模型可表現大量元素形狀，包括剛柔性和凹凸性。當其中1個活動半徑為負時，模型即表現凹形狀。

1.2 重 構

紋樣重建，即對紋樣中的每個元素，選用合適的模型實例替代之，從而得到模型化的數字紋樣。首先需要從藍印花布紋樣圖像中提取紋樣元素，然后從大量模型實例中找出與之最接近的，將該模型實例進行仿射變換應用到紋樣空間以替代紋樣元素。

1.2.1輪廓跟蹤

輪廓跟蹤法[8]可用來對二值圖像中的目標進行輪廓提取。二值圖像中存在目標和背景2類像素，通常目標像素(白色)值為1而背景像素(黑色)值為0。輪廓跟蹤方法的步驟如下：

1) 按照從左到右、從上到下的順序逐行掃描像素矩陣，直至發現第1個目標像素P，記下P點位置。

2) 設定P點的初始搜索方向為沿左下方，搜索方向每次逆時針累加旋轉45°，直至找到第2個邊界點Q，記下Q點的位置。

3) 將當前搜索方向順時針旋轉90°，作為Q點的初始搜索方向，搜索方向每次逆時針累加旋轉45°，直至找到下一個邊界點，令該點為新的Q點，記下位置。

4) 重復步驟3)，直至回到最初的P點。

圖6為輪廓跟蹤示意圖。其中：空心圓點Q1～Q13表示搜索到的各個邊界點；在每個邊界點上，實線箭頭表示初始搜索方向。

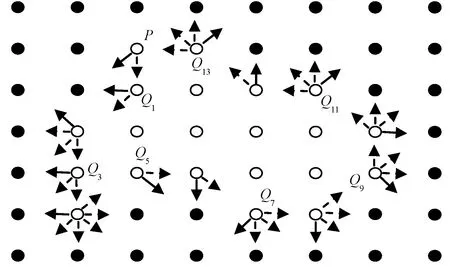
圖6 輪廓跟蹤原理圖Fig.6 Schematic of contour tracing

以藍印花布掃描圖像為原始素材，在進行輪廓跟蹤提取紋樣元素前，需要進行一些必要的預處理，主要步驟如圖7所示。

圖7 元素提取的步驟Fig.7 Procedures of element extraction. (a) Original image (grayed); (b) Median filtering; (c)Threshold segmentation; (d)Contour tracing

原始圖像經灰度化后，先通過中值濾波[9]去除噪聲；再使用OTSU算法[10]進行閾值分割，分離出目標與背景；最后，使用輪廓跟蹤算法提取圖像中每個紋樣元素的矢量輪廓。

1.2.2模型實例選取

圖像的Hu矩對應了一系列圖像，這些圖像可由其中任何一個平移、縮放和旋轉得到。換言之，Hu具有平移、縮放和旋轉不變性[11]。對于數字圖像f(x,y)，其p+q階標準矩mpq定義為

(5)

其中，N和M分別是圖像的高度和寬度。數字圖像的p+q階中心矩μpq定義為

(6)

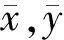
(7)

圖像的Hu矩是基于歸一化中心矩jpq的1組不變矩，它由7個特征值(M1～M7)組成：

(8)

形狀是圖像的特例，形狀f(x,y)的值域只有2個可能：0或1。當點(x,y)在形狀輪廓線上時，值為1；否則為0。本文研究涉及的模型形狀和元素形狀，均可轉換為數字圖像，從而利用Hu矩的不變性。進行實例選取時，先計算紋樣元素的Hu矩，然后比對元素形狀與每個模型實例的接近程度(2個Hu矩的歐式距離)，找出最接近的模型實例，結果如圖8(b)所示。其模型參數為t=1.2,r0=0.5,d0=0,r1=1,d1=0。

圖8 基于Hu矩的模型實例選取Fig.8 Instance selection based on Hu moments.(a) Pattern element; (b) slosest model instance

1.2.3模型實例變換

最接近(或對稱)實例與元素形狀相似度最高，需要對其進行仿射變換(平移、縮放和旋轉)，使之盡量與元素形狀重合，以替代紋樣元素。考慮到形狀重合的2個必要條件：形狀幾何重心一致；形狀面積相等。

圖9 實例變換過程Fig.9 Procedures of instance transform

其次，計算二者面積之差，若大于零(模型實例面積大于元素面積)則將模型形狀逐步縮小，否則逐步放大，直到二者面積相等，此時的縮放率記為s。

最后，將模型實例在0°～360°上旋轉，計算每個角度上模型實例與紋樣元素的重合度，記取重合度最大的角度θ。

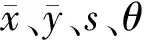
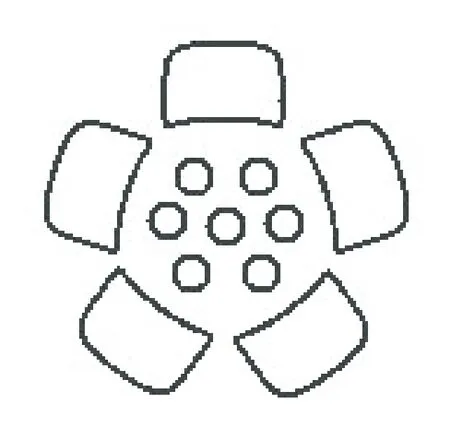
圖10 重構的紋樣Fig.10 Reconstructed pattern

1.2.4映射函數

對模型匹配后的數字化紋樣，使用映射函數將模型參數映射到新的區間，實現紋樣創新。參與映射的可以是構形參數，也可以是仿射參數。圖11示出對數字化紋樣進行重構的圖例。

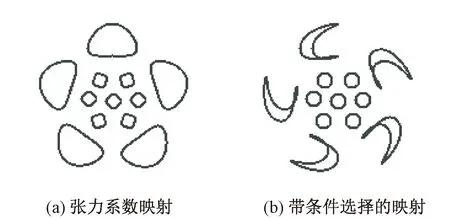
圖11 通過映射函數進行的紋樣改造Fig.11 Modifications by mapping functions. (a) Mapping of tension coefficient; (b) Mapping with conditions

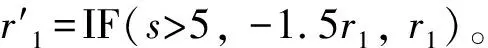
2 結果與討論

2.1 泛化的模型

本文研究提出的模型使用4個節點，按特定的順序定義4條首尾相連、平滑過渡的基數樣條曲線，形成封閉形狀。利用張力系數表現形狀的剛柔性，通過定義活動節點實現了形狀的凹凸性和多樣性。實驗結果證明，該模型能夠很好地表現大多數傳統藍印花布紋樣元素。但仍有一些紋樣元素超出了其能夠表達的范圍，特別是那些由于不便在傳統工藝下印制而在實踐中較少采用的元素[2]。這些元素超出了4節點樣條曲線所能表現的范圍，如圖12所示。表現這樣的元素形狀需要更多節點和更復雜的模型，這種模型可由上述4節點模型泛化而來。

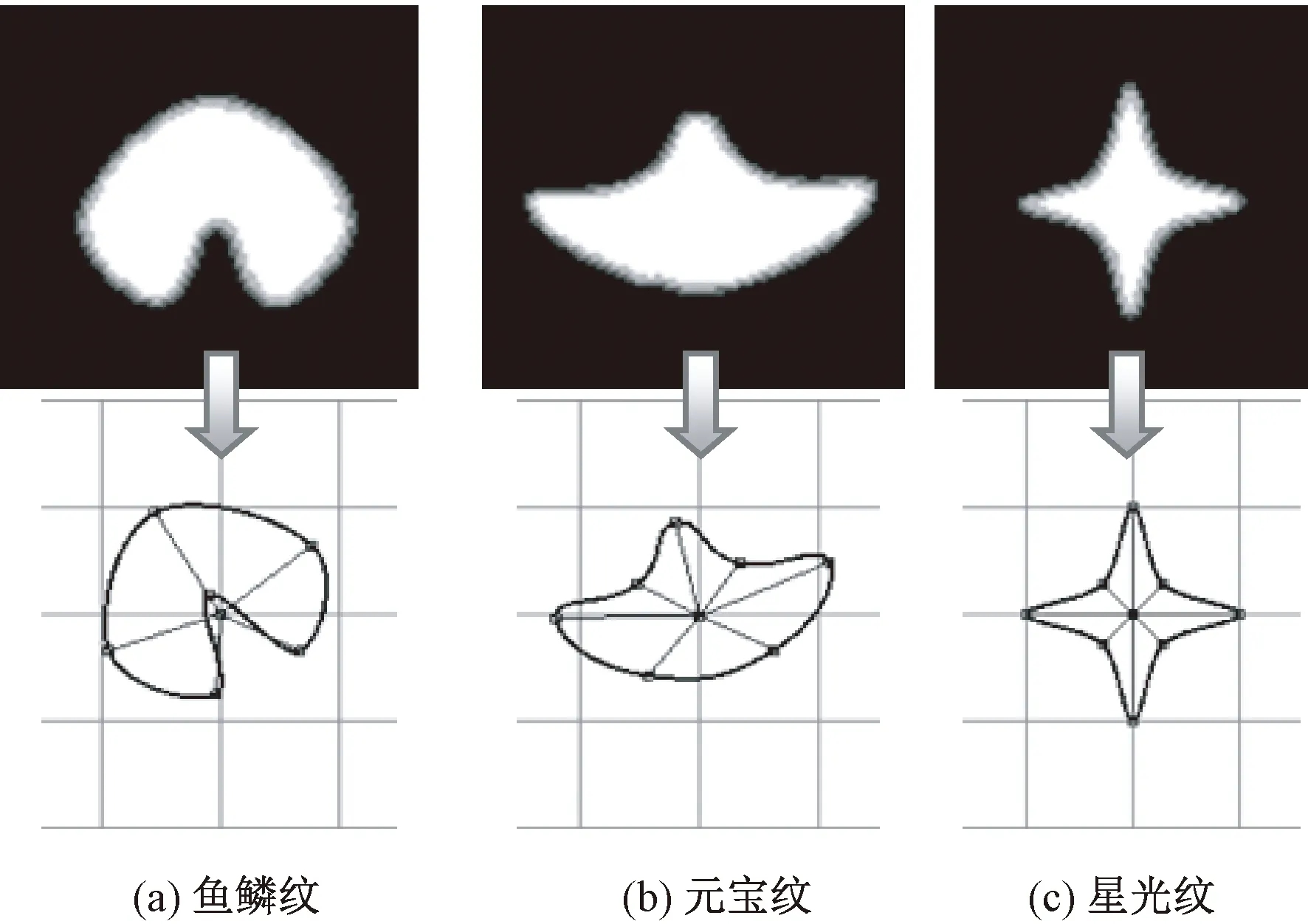
圖12 利用泛化模型表達復雜元素Fig.12 Complex elements expressed in generalized model.(a)Scale pattern; (b)Treasure pattern; (c)Starlight pattern

圖12(a)為魚鱗紋，模型參數為t=0.9,r0=0.75,d0=27,r1=-0.2,d1=0,r2=0.75,d2=-27,r3=1,d3=-20,r4=1.1,d4=0,r5=1,d5=20；圖12(b)為元寶紋，模型參數為t=0.7,r0=1.2,d0=-25,r1=0.7,d1=-25,r2=0.7,d2=25,r3=1.2,d3=25,r4=0.6,d4=5,r5=0.9,d5=0,r6=0.6,d6=-5；圖12(c)為星光紋，模型參數為t=0.8,r0=1,d0=0,r1=0.4,d1=0,r2=1,d2=0,r3=0.4,d3=0,r4=1,d4=0,r5=0.4,d5=0,r6=1,d6=0,r7=0.4,d7=0。

設有n(n≥4)個節點(記為P0,P1,P2，…，Pn-1)，以順時針方向分布于單位圓(半徑為1)的圓周等分點上，2個相鄰節點之間的圓心角為(360/n)°，點O為圓心或參考點，如圖13(a)所示。

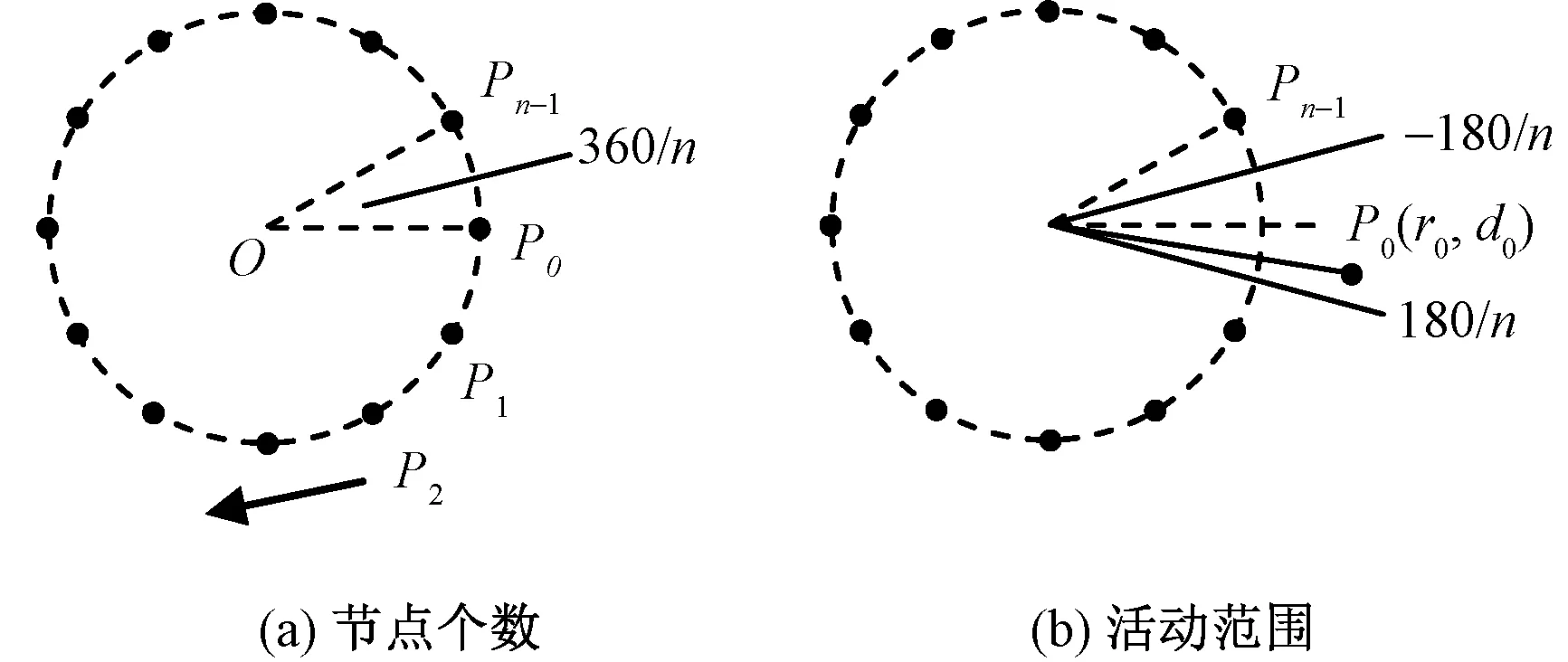
圖13 泛化模型Fig.13 Generalized model. (a)Number of knots; (b)Range of activity

規定每個節點可以偏離所在的等分點，其坐標位置由活動半徑ri(-10≤ri≤10)和偏離角di(-180/n≤di≤180/n)決定，如圖13(b)所示。使用基數樣條，按如下順序連接所有節點以構成封閉形狀：(P0,P1,P2,P3),(P1,P2,P3,P4)，…，(Pn-1,P0,P1,P2)。當n=4且固定節點P2,P3時，即為本研究中所使用的4節點模型。

此泛化模型中，每個節點對應2個參數(活動半徑和偏移角)，另外加上張力系數，模型中的參數個數為2n+1，模型實例的數量為m2n+1(m為取樣次數)。只要節點數量足夠多，模型就可以表達復雜紋樣元素。使用6節點、7節點及8節點模型表現復雜元素，如圖12所示。但節點增加，意味著模型參數的增加，造成重構過程運算量大幅上升。實際應用中可根據紋樣元素的復雜程度決定n的取值。

2.2 作為骨架的模型

目前為止，本文研究提出的模型是針對紋樣元素的，但實際上它也可以作為紋樣的骨架，進而實現更高層次上的建模。總體來說，藍印花布紋樣主要呈現2種基本的骨架，即環形骨架和線形骨架，如圖14中虛線所示。

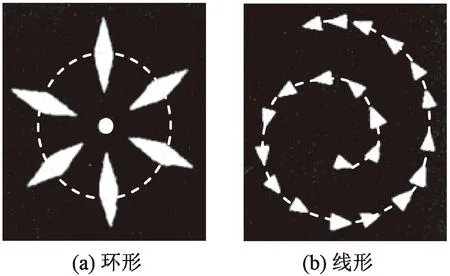
圖14 2種基本骨架Fig.14 Two basic skeletons. (a) Circular; (b) Threaded

在環形骨架中，骨架線上的紋樣元素圍繞一個中心點分布，該點稱為骨架中心；而在線形骨架中，紋樣元素根據骨架線的切線方向分布。需要注意的是，環形骨架的骨架線不一定是圓形，可以是任何閉合的形狀。大多數復雜的紋樣都可分解為這2種骨架的組合。

若以圖15所示的圓紋作為紋樣骨架，構成骨架的點集(xi,yi)可由式(1)中模型的樣條定義取得。其中：i=0,1,2，…,k-1；k是骨架線上的總點數。

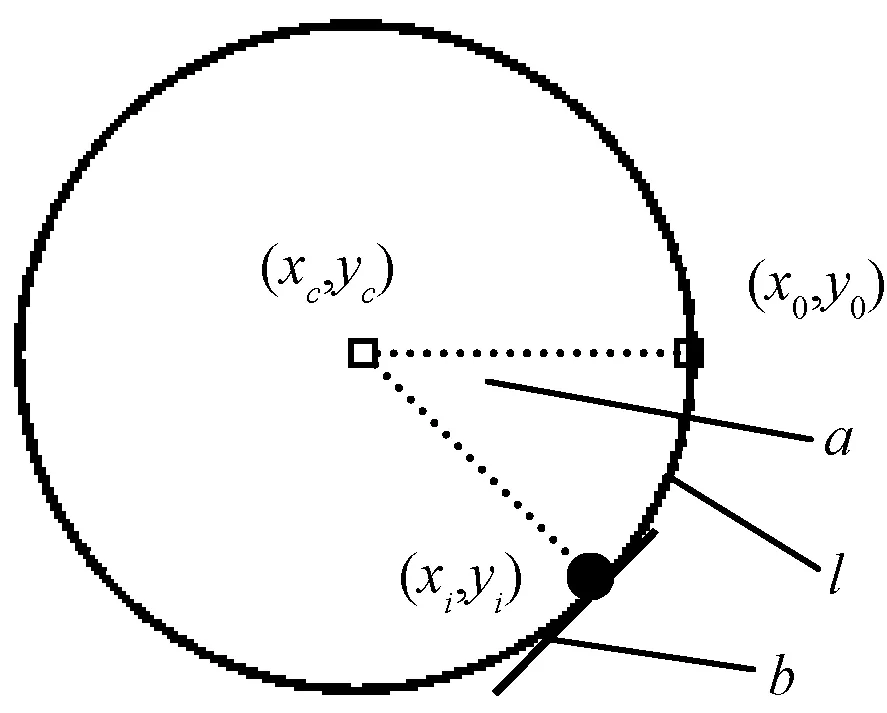
圖15 作為骨架的模型Fig.15 Model as skeleton

點(x0,y0)是骨架的起點，模型的原點(xc,yc)可作為骨架的中心點(在線性骨架中，該點可以忽略)。骨架上的每個點(xi,yi)擁有3個屬性，即中心角(以a表示)、切線角(以b表示)和步長(以l表示)。中心角是骨架起點、中心點及當前點構成的角度；切線角是當前點在骨架線上的切角；步長是沿骨架線從起點到當前點的路徑長度。這3個屬性可通過下式計算：

(9)

(10)

(11)

另外，骨架線的總長度(以L表示)為

(12)

沿骨架線進行紋樣元素的分布，稱為骨架的具化。上述3個屬性將對骨架的具化產生影響。在實施骨架具化前，構造1個種子元素(由5個構形參數和4個仿射參數決定)，1個定位器函數(Dp)和1個定形器函數(De)。定位器根據步長決定是否放置元素，在放置元素時定形器負責對種子元素實施調整，即根據當前中心角或切線角對種子元素的構形參數和仿射參數進行調整，實現骨架線上紋樣元素的變化。骨架具化的例子如圖16所示。

在圖16 (a)中，以方紋為骨架，用柱狀紋作為種子元素對其進行具化。定位器沿骨架路徑每隔L/8放置紋樣元素，定形器將元素的旋轉角θ(元素模型的仿射參數之一)設置為骨架中心角a的線性函數，從而實現了環形骨架。圖16(b)中的定形器在圖16(a)基礎上增加了對張力系數t的控制，通過將當前值設為對最近一次張力系數值(tprev)遞增，實現骨架上紋樣元素剛柔性的漸變。圖16(a)、(b)的骨架具化函數如下：

圖16 (c)、(d)中的紋樣都以貝殼紋作為骨架、以米粒紋作為種子元素。二者的區別在于，前者的定形器以中心角a作為參數產生了環形骨架，而后者的定形器以切線角b作為參數產生了線形骨架。可見，骨架具化過程中產生環形或線形骨架，取決于定形器使用中心角還是切線角作為參數。圖16(c)、(d)的具化函數如下：

圖16(e)、(f)中，都使用定形器產生環形骨架，同時對元素的縮放率s進行調整，通過將當前值設為對最近一次縮放率(sprev)的倍數，帶來了骨架線上元素尺寸的漸變。圖16(f)中的定位器引入了非線性函數，因此與圖16(e)相比，骨架線上元素間的間隔不是均勻的而是遞增的。圖16 (e)、(f)的具化函數如下：

上述實例展示了作為骨架的模型對2種基本骨架的模擬，以及通過模型參數變化帶來的創新。其中元素的漸變和非線性分布是對傳統藍印花布紋樣的創新性改造。

3 結 論

本文研究基于基數樣條曲線對藍印花布紋樣元素建模，利用張力系數表達形狀的剛柔性，通過配置活動節點實現形狀的凹凸性和多樣性。對于一些超出4節點模型表達范圍的形狀，可通過泛化模型覆蓋。在紋樣重構方面，先使用輪廓跟蹤技術從圖像中提取紋樣元素，然后利用Hu矩的不變性選取與之最接近的模型實例，再利用矢量形狀的重心、面積及重合度對模型實例進行仿射變換，將其應用到紋樣空間，完成紋樣數字化。對數字化紋樣，通過映射函數調節模型參數進行紋樣元素的改造和創新。對于擁有閉合骨架的紋樣，通過將元素模型應用到骨架進行紋樣骨架的改造，再利用定位器和定形器實施骨架具化，完成更為深刻的改造。實驗結果證明，本文模型及其泛化版本可以很好地表現絕大多數藍印花布紋樣元素，該模型用于紋樣骨架也可帶來豐富的創新效果。

FZXB