斯特林制冷機間隙密封泄漏的分子動力學模擬
穆德富,祁影霞,孟祥麒
(上海理工大學 能源與動力工程學院,上海 200093)
1816年,Stirling提出了一種由兩個等溫壓縮和膨脹過程與兩個等容回熱過程組成的閉式熱力循環,稱為斯特林循環。1862年,Krik將斯特林循環的逆循環用于制冷并獲得成功,該循環稱為逆向斯特林循環,也稱斯特林制冷循環[1]。早期的斯特林制冷機的可靠性和壽命問題限制了它的應用空間。傳統的斯特林制冷機一般采用活塞環實現密封,這種密封存在磨損,因而工作壽命受到限制。由運動部件上的密封環摩擦帶來的污染及密封環本身的磨損是影響制冷機使用壽命、增加泄漏的一個重要因素。直到牛津型斯特林制冷機的出現,制冷機的穩定性和壽命才得以大大提高。牛津型斯特林制冷機是20世紀80年代初,由牛津大學Davy首次在制冷機中采用線性驅動、間隙密封、擺線懸梁板彈簧支撐、工質泄漏污染等關鍵技術而研制成功的制冷機。
這類制冷機的壓縮機活塞由直線電機驅動自由壓縮活塞,采用線性驅動的制冷機在壽命上占優勢,不但減少了運動部件,簡化了結構,而且大幅度減少了干擾。非線性壓縮機的金屬部件之間使用潤滑油以形成液膜用于潤滑和冷卻運動部件[2],潤滑油也起到一定的密封作用。而自由活塞斯特林制冷機采用板彈簧支撐的間隙密封,利用板彈簧的軸向剛度小、徑向剛度大來保證活塞與氣缸的間隙密封[3]。與傳統的環密封相比,間隙密封軸孔兩零件采用間隙配合,使兩零件無接觸。因此,摩擦損失減小,提高了制冷機的壽命。斯特林制冷機一般采用少量氦氣作為制冷工質,整個循環無相變[4]。由于有間隙的存在,當密封兩端壓力不相等時會引起氣體的泄漏,所以必須考慮由于氣體泄漏而造成的冷量損失。
Bailey等[5]通過測量活塞移動位置來測量間隙密封的層流流動,以此估計在特定行程下的間隙密封損失;陳曦等[6]推導了活塞運動和交變壓力波同時存在情況下,環形間隙的泄漏量和一個周期內的平均泄漏量的計算公式,指出泄漏由活塞振動和壓差兩部分組成;龔俊等[7]建立了層流工況下斯特林發動機氣缸與活塞間隙密封的數學物理模型,推導了密封間隙的泄漏量,最后與理想條件下的泄漏量進行比較,得出實際工況和由位置偏心引起的密封間隙的泄漏量較理想狀態下泄漏量大;馬詩旻等[8]研究得出,壓力波和間隙寬度對泄漏量的影響較大,隨充氣壓力、壓比以及間隙的增大,泄漏量增加;盧明[9]分析了幾種形式的間隙密封的流動特性,并使用Fluent軟件對間隙密封在穩態層流、不可壓、定溫、定黏度、內外壁面無相對滑動的條件下進行了數值模擬,模擬結果與理論推導非常接近。
過去對間隙泄漏的研究主要集中在穩定層流、不可壓縮、恒定溫度的條件下使用流體力學方法的數值模擬。本文提出一種通過分子動力學模擬的方法來研究間隙密封的泄漏機理,分析泄漏機理、壓差對泄漏量的影響。
1 模擬的基本原理和方法
1.1 基本原理
分子動力學模擬是根據牛頓力學原理發展起來的計算方法。該方法最早由Alder[10]于1957年引入分子體系,其基本原理是通過牛頓經典力學計算物理系統中各個原子的運動軌跡,然后使用一定的統計方法計算出系統的力學、熱力學、動力學等性質。在分子動力學中,首先將由N個粒子構成的系統抽象成N個相互作用的質點,每個質點具有坐標(通常在笛卡兒坐標系中)、質量、電荷及成鍵方式,按目標溫度根據Boltzmann分布[11]隨機指定各質點的初始速度,然后根據所選用的力場中相應的成鍵和非鍵能量表達形式對質點間的相互作用能以及每個質點所受的力進行計算。接著依據牛頓力學計算出各質點的加速度及速度,從而得到經一指定積分步長(通常為1 fs)后各質點新的坐標和速度,這樣質點就移動了。經一定的積分步數后,質點就有了運動軌跡,同時設定一定的時間間隔對軌跡進行保存。最后對軌跡進行各種結構、能量、熱力學、動力學、力學等分析,從而得到所需要的計算結果。
1.2 模擬方法
利用Materials Explorer軟件模擬建立由鐵原子晶體與氦原子組成的物理模型。物理模型如圖1所示,圖中:L為壓縮腔長度;d為間隙寬度。首先,建立He制冷劑在間隙內部的周期性邊界條件,在背壓腔端和壁面1的右側,設置一定容積的He,標記為He1,在壁面3的左側空間,設置與He1同樣壓力的He2,壁面設置為一定空間規則排布的Fe原子。整個泄漏的模擬過程為He氣體從背壓腔通過寬度為d的間隙到達壓縮腔,壁面1和壁面2均由Fe原子構成,其中長度、寬度、高度方向上分別設置800、5、2個晶胞。由于Fe原子的晶胞都是緊密排列的,每個晶胞為 2.860 6 ?(1 ?=10-10m),由鐵原子晶胞組成壁面。該狹縫用來模擬斯特林制冷機中的間隙密封的寬度,將氦氣固定在狹縫的另一端,作為氣體源,通過改變狹縫一端的氦氣壓力來模擬密封間隙內壓力變化對泄漏的影響。
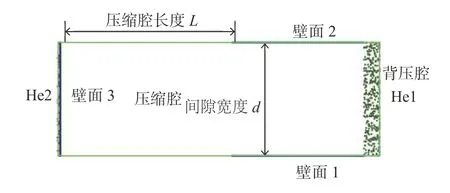
圖1 物理模型Fig.1 Physical model
用于Fe原子之間的勢能函數是Johnson勢能函數,He原子與He原子以及He原子與Fe原子之間采用UFF勢能函數。模擬在NVT系綜進行,溫度保持在298 K,時間步長為0.8 fs,模擬以10 000步的速度執行。總的運行過程是以這個速度連續運行,將建好的物理模型上傳到服務器中進行計算。運行一段時間后,統計從間隙中泄漏出的He原子數。
2 模擬結果及分析
2.1 He 原子運動軌跡分析
選取在壓力p= 200 kPa,溫度T= 298 K,d=2 000 ?,運行時間為 184 ps(1 ps = 1.0 × 10-12s)的He原子速度矢量圖,如圖2所示。從圖中可看出,當d= 2 000 ?時,在靠近壁面處 He 原子的密度大于中間原子的密度,在壁面附近,邊界層黏滯阻力以及He原子與Fe原子相互作用力影響He原子向壓縮腔泄漏的進程,而中間的He原子由于受到的影響小,向壓縮腔方向的泄漏進程變慢。從速度矢量上看,垂直于壁面的原子是不可能泄漏的,只有速度矢量與壁面呈一定夾角的原子,才有可能泄漏。
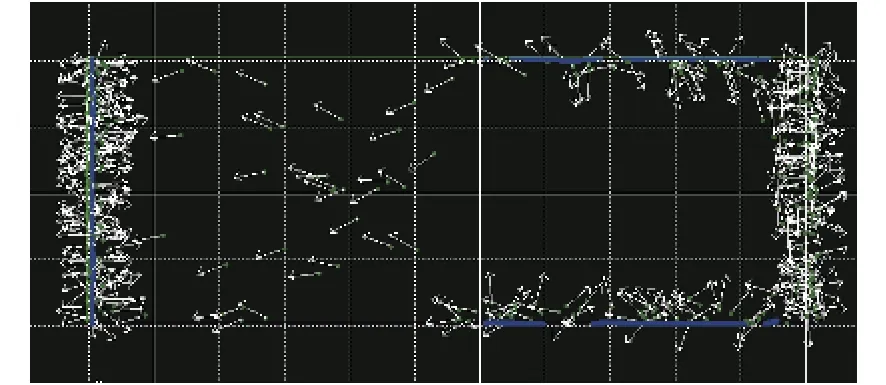
圖2 He 原子速度矢量圖Fig.2 Diagram of He actom velocity vector
2.2 不同壓力下間隙泄漏量隨時間的變化
在間隙寬度為2 000 ?,其他條件不變時,模擬了不同壓力下的泄漏量,統計出在不同壓力下泄漏分子數隨時間的變化,結果如圖3所示。
由圖中可知,間隙內He原子分別在p= 200、400、600、800 kPa下開始泄漏的時刻不同,總體趨勢均為泄漏量隨壓力的增大而增大。
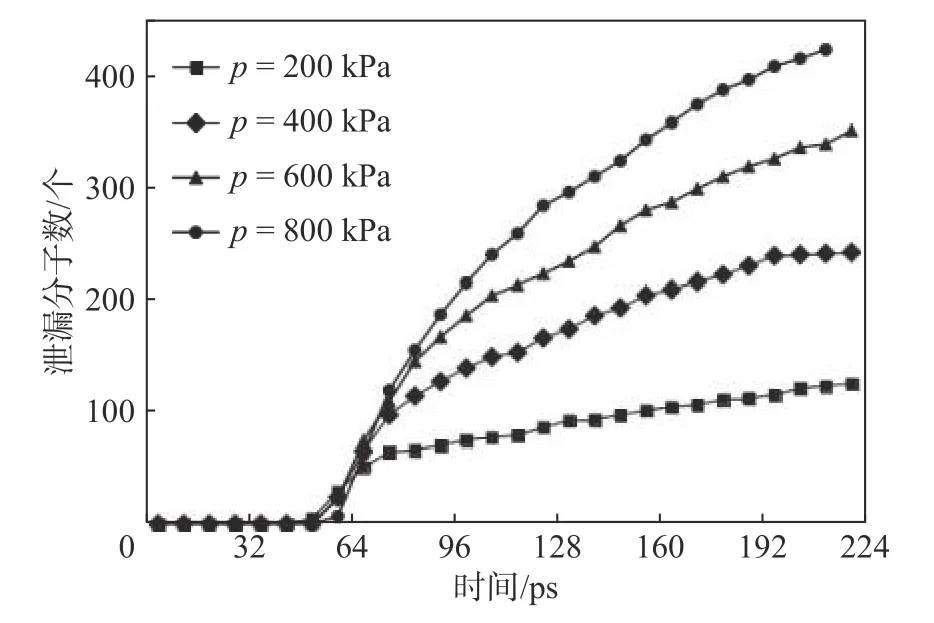
圖3 不同壓力下泄漏分子數的變化Fig.3 Changes of the leakage molecular number under different pressures
圖4為不同壓力下泄漏速率的變化,其中時間段 0~8 ps以 1 代替、8~16 ps以 2 代替,依此類推作為橫坐標數值。從圖中可看出,密封間隙內He原子從背壓腔到壓縮腔的泄漏速率先遞增后遞減,最后穩定在一定值。隨著壓力增大,泄漏速率峰值增大,并且最大峰值出現的時刻也推遲。一方面,由于背壓腔與壓縮腔的壓差增大,必然引起He原子向壓縮腔運動的動能增大,泄漏速率增大。而隨著時間推移,壓縮腔內He原子數增加,其背壓腔與壓縮腔的壓差逐漸減小,導致泄露速率逐漸減小。當兩腔體之間壓差穩定后,其泄露速率也相對平穩;另一方面,壓差增大也會引起He原子之間的運動變得劇烈,相互之間的膨脹加劇,向壓縮腔方向的運動也會受到影響,因此達到最大泄露速率的時間相對滯后。
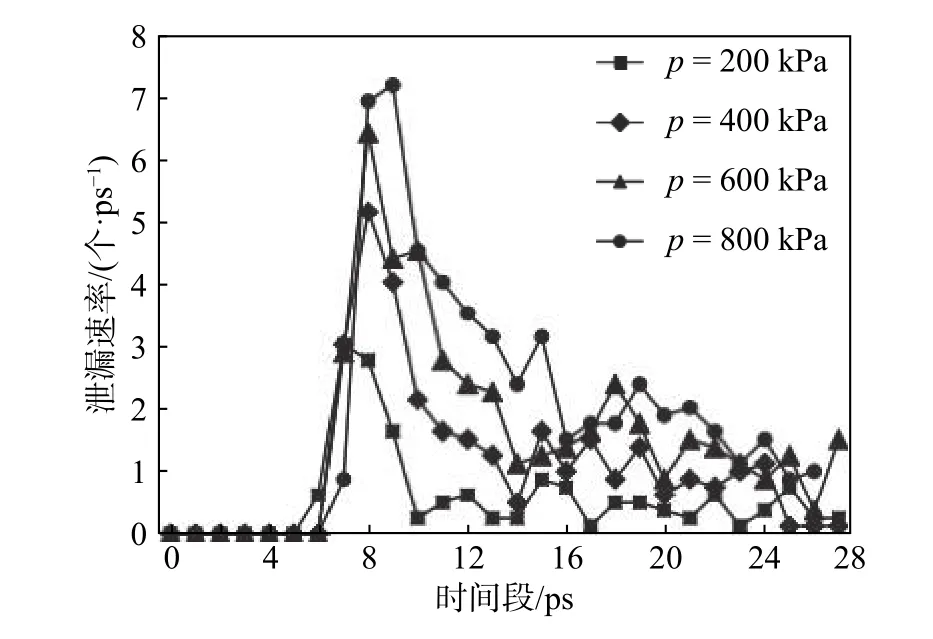
圖4 不同壓力下泄漏速率的變化Fig.4 Changes of the leakage rate under different pressures
2.3 不同間隙寬度下泄漏量隨時間的變化
在壓力為200 kPa,其他條件不變時,模擬了在間隙寬度不同時的泄漏量。根據模擬結果,統計出當d分別為 2 000、3 000、4 000、5 000 ?時泄漏分子數隨時間的變化,結果如圖5所示。從圖中可以看出:泄漏量隨著時間的推移逐漸增大;不同間隙寬度的泄漏量不同,隨著間隙寬度的增大,泄漏量增大。
圖6為不同間隙寬度下泄漏速率的變化,其中時間段 0~8 ps以 1 代替、8~16 ps以 2 代替,依此類推作為橫坐標數值。從圖中可以看出,密封間隙內的He原子從背壓腔到壓縮腔的泄漏速率先遞增后遞減,最后趨于穩定。隨著間隙寬度的增大,泄漏速率峰值也增大。這是由于隨著間隙寬度的增大,泄漏的橫截面變大,導致更多的He原子通過橫截面進入間隙中,造成泄漏量增多。隨著時間的推移,壓縮腔內He原子數增加,壓差減小,泄漏速率減小,并逐漸達到一個穩定的狀態。
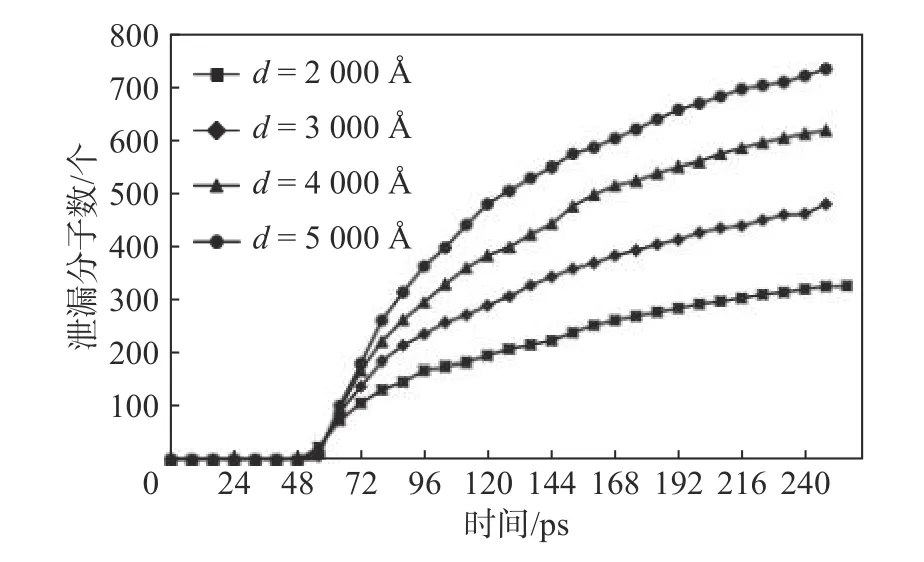
圖5 不同間隙寬度下泄漏分子數的變化Fig.5 Changes of the leakage molecular number under different gap width
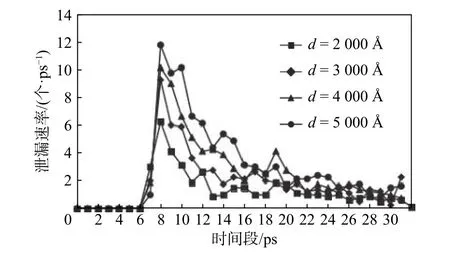
圖6 不同間隙寬度下泄漏速率的變化Fig.6 Changes of the leakage rate under different gap width
3 結 論
(1)通過分析整個模擬過程發現:在壁面附近He原子的密度大于在中間位置的密度;速度垂直于壁面的原子是不可能泄漏的,只有速度矢量與壁面呈一定夾角的原子才有可能泄漏。
(2)泄漏量隨著間隙內壓力和間隙寬度的增大逐漸增大,所以應在保證斯特林制冷機正常運行下,選擇合適的壓力,盡量減小間隙寬度,減小泄漏量,提高制冷機的效率。

