基于OpenSEES的鋼筋混凝土柱擬靜力分析*
薛興偉, 龐 興, 周俊龍
(沈陽建筑大學 交通工程學院, 沈陽 110168)
鋼筋混凝土結構在地震作用下進入非線性狀態并產生損傷,地震作用下鋼筋混凝土構件的非線性行為,對結構的抗震性能評估有重要意義.有限元法作為強大的數值分析方法,在鋼筋混凝土構件的非線性分析中發揮的作用日益顯著,而鋼筋混凝土是由混凝土和鋼筋這兩種性質差別很大的材料結合而成的組合材料,其性能明顯依賴于這兩種材料的性能,但在非線性階段,混凝土和鋼筋本構參數的合理設置,決定了鋼筋混凝土構件數值模擬分析的準確性.
目前有許多通用軟件,在模擬結構的非線性反應時存在許多的局限性,算法的容錯能力較差,當程序內部的固定算法不能完成收斂時,不能更換成更高效的算法,如SAP2000和MIDAS等.ABAQUS軟件在保證相同計算精度條件下,計算量通常較大.OpenSEES軟件適用于鋼筋混凝土結構的擬靜力分析、動力非線性分析等,其強大的非線性處理能力保證了計算的高精度與高效率,已廣泛應用于世界范圍內的高校和科研機構.
杜柯等[1]基于有限元軟件OpenSEES中的3種非線性單元,對纖維模型中單元、截面以及纖維的劃分問題進行了研究;張行等[2]考慮鋼筋屈曲效應,采用非線性纖維單元對4根鋼筋混凝土柱的擬靜力試驗進行了數值模擬;孫廣俊等[3]基于OpenSEES平臺,分別采用梁柱纖維單元和帶塑性鉸梁柱纖維單元建立了鋼筋混凝土單柱的纖維模型和纖維鉸模型,對循環荷載下的鋼筋混凝土單柱非線性滯回反應進行了數值模擬.
上述研究未對材料本構模型具體參數的設置進行詳細闡述和對比研究.本文基于有限元軟件OpenSEES中非線性纖維單元,對文獻[4]以彎曲破壞為主的4根鋼筋混凝土柱擬靜力試驗進行Concrete02材料λ參數、P-Δ效應、鋼筋強化系數、軸壓比及配箍率數值模擬,通過對比分析,給出了混凝土和鋼筋本構相關參數設置的建議.
1 試件簡介
本文選取的鋼筋混凝土構件的截面尺寸與配筋如圖1所示(單位:mm).
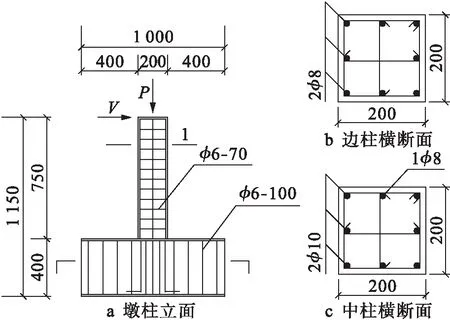
圖1 構件配筋Fig.1 Reinforcement of components
邊柱水平加載依次為10、20、30 kN,荷載循環一圈,此后以水平力控制加載,所加位移依次為10、15、20、25、30、37.5、55 mm,各級循環兩圈;中柱水平加載依次為10、20、30、40 kN,荷載循環一圈,此后以水平力控制加載,加載位移和循環圈數與邊柱相同.
2 材料本構模型
2.1 混凝土本構模型
混凝土采用基于Kent-Park模型的Concrete02模擬.在程序中,Concrete02材料定義的命令為uniaxialMaterial Concrete02,matTag,fpc,epsc0,fpcu,epsU,λ,ft,Ets[5].具體本構模型如圖2所示.
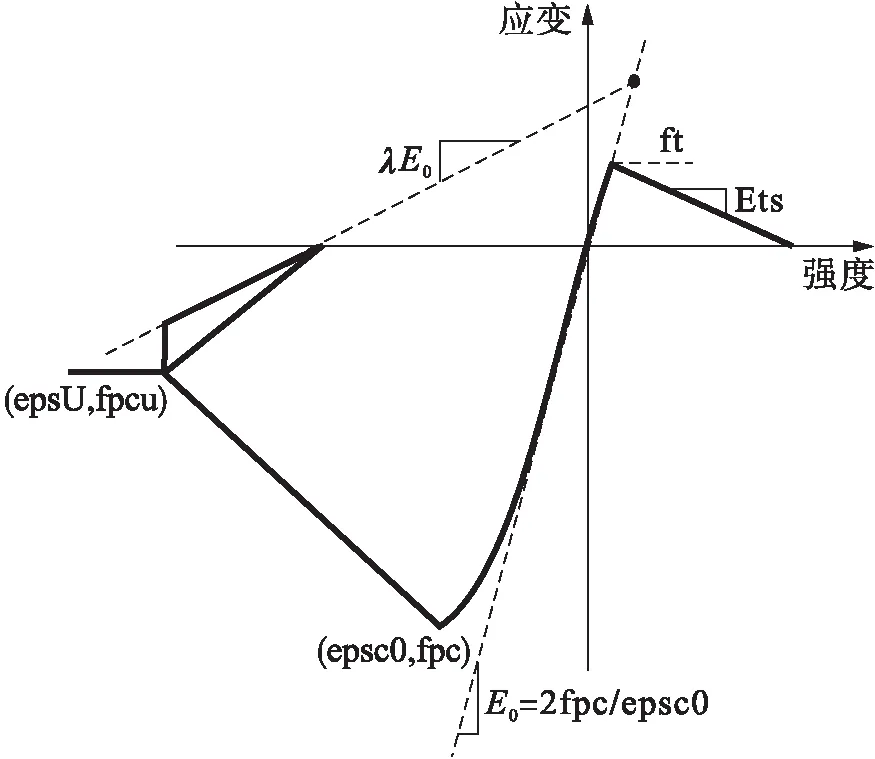
圖2 Concrete02本構模型Fig.2 Constitutive model for Concrete02
一般混凝土試驗數據涉及混凝土的強度,無法確定混凝土即將破壞時對應的混凝土彈性模量E,而在Concrete02本構關系中,λ=E/E0,故本文對λ參數進行計算分析,以期在無相關試驗數據情況下,給出合理設置的相關建議.
2.2 鋼筋本構模型
受力鋼筋采用基于修正后的Menegotto-Pinto本構模型中的Stee102[6],以反映Bauschinger效應的影響.在程序中,Stee102材料定義的命令為uniaxialMaterial Steel02,matTag,Fy,E,b,R0,cR1,cR2,a1,a2,a3,a4,sigInit.
鋼筋混凝土柱在地震作用或擬靜力荷載作用下,鋼筋是否能充分發揮拉伸試驗得到的強化系數存在著不確定性,故對Stee102材料中的鋼筋強化系數b值進行探討,給出合理設置的相關建議.
3 參數分析
3.1 Concrete02本構參數
λ參數為混凝土卸載時對應的卸載斜率與混凝土加載時的初始斜率E0的比值[7],即卸載斜率為λE0,而對應位置處重新加載對應的斜率為2λE0,故λ對混凝土后期加載的滯回曲線形狀影響明顯.

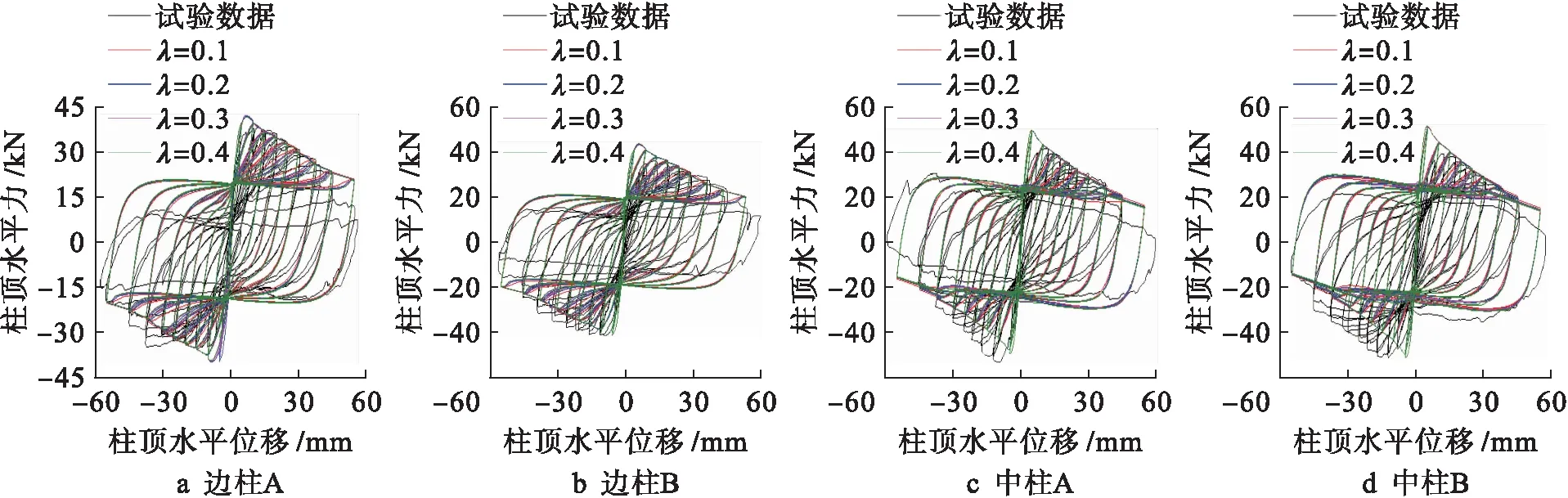
圖3 λ滯回曲線Fig.3 λ hysteresis curves
3.2 P-Δ效應
圖4為分析P-Δ效應對4個框架柱抗震性能的影響得到的相關滯回曲線[8],可以看出考慮P-Δ效應,數值模擬滯回曲線與試驗滯回曲線吻合較好,而不考慮P-Δ效應,數值模擬的4個框架柱的峰值荷載明顯比試驗峰值荷載要高,后期的骨架曲線對應的承載力明顯比試驗結果高,模擬效果不理想,高估了鋼筋混凝土柱在擬靜力荷載作用下的承載能力,因此,在做墩柱擬靜力試驗數值模擬分析時應考慮P-Δ效應.
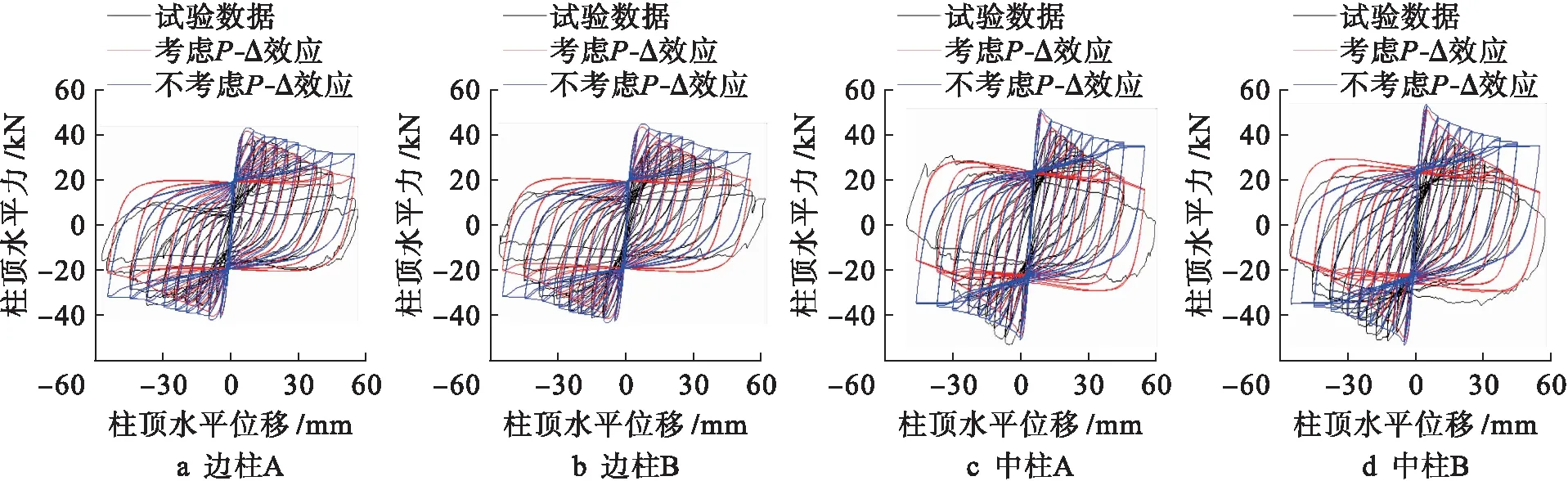
圖4 P-Δ滯回曲線Fig.4 P-Δ hysteresis curves
3.3 鋼筋強化系數
為了分析鋼筋強化系數[9]對框架柱抗震性能的影響,鋼筋強化系數b分別取0.001、0.01、0.1.由圖5可以發現,隨著鋼筋強化系數b的增大,對構件峰值荷載影響不大,但當構件承載力達到峰值點荷載后,構件的骨架曲線發生顯著變化,下降段斜率明顯變緩,甚至下降段轉變為上升段,承載能力明顯提高,同時卸載后在反向加載過程中,剛度變大.
本文模擬的4個框架柱采用的鋼筋類型為光圓鋼筋,其拉伸試驗測得的極限強度與屈服強度的比值均大于1.45,表現出了光圓鋼筋屈服后具有較高的抵抗變形的能力.由圖5可以看出,鋼筋強化系數b為0.001時與試驗模擬結果相近,吻合效果較好.當鋼筋強化系數b值增大到0.1時,承載能力明顯提高,模擬效果不理想,高估了框架柱在擬靜力作用下的承載能力.
因此,在做墩柱擬靜力試驗數值模擬分析時應不考慮或考慮較小的鋼筋強化系數,建議其取值范圍為0~0.01.
3.4 軸壓比與配箍率
根據上述數值模擬與試驗數據對比分析得到的結果,擴大研究范圍,建立邊柱A有限元數值模型時取參數λ為0.15,考慮P-Δ效應,鋼筋強 化系數b取0.001;改變邊柱A的配箍率,分析其在軸壓比分別為0.07、0.10、0.15、0.20時對鋼筋混凝土柱抗震性能的影響.
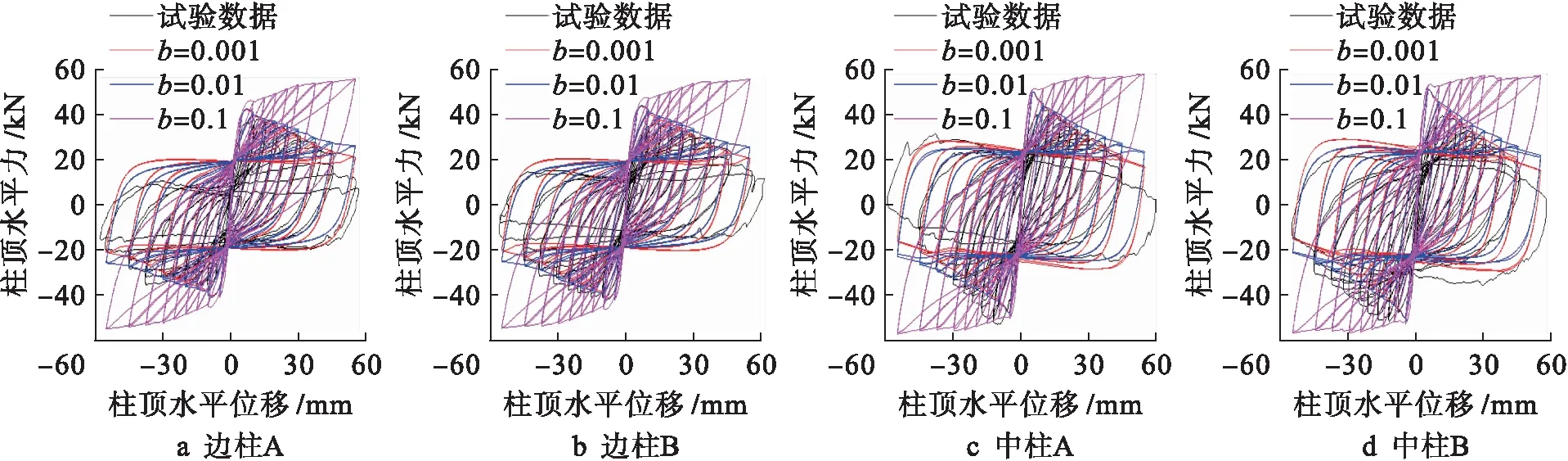
圖5 鋼筋強化系數b滯回曲線Fig.5 Reinforcement strengthening factor b hysteresis curves
構件的耗能能力一般由滯回曲線包圍的面積來評定,面積大則耗能能力強[10].由圖6~8可以看出,在配箍率相同的條件下,隨著軸壓比的增大,框架柱滯回曲線包圍的面積逐漸減少,耗能能力明顯降低.
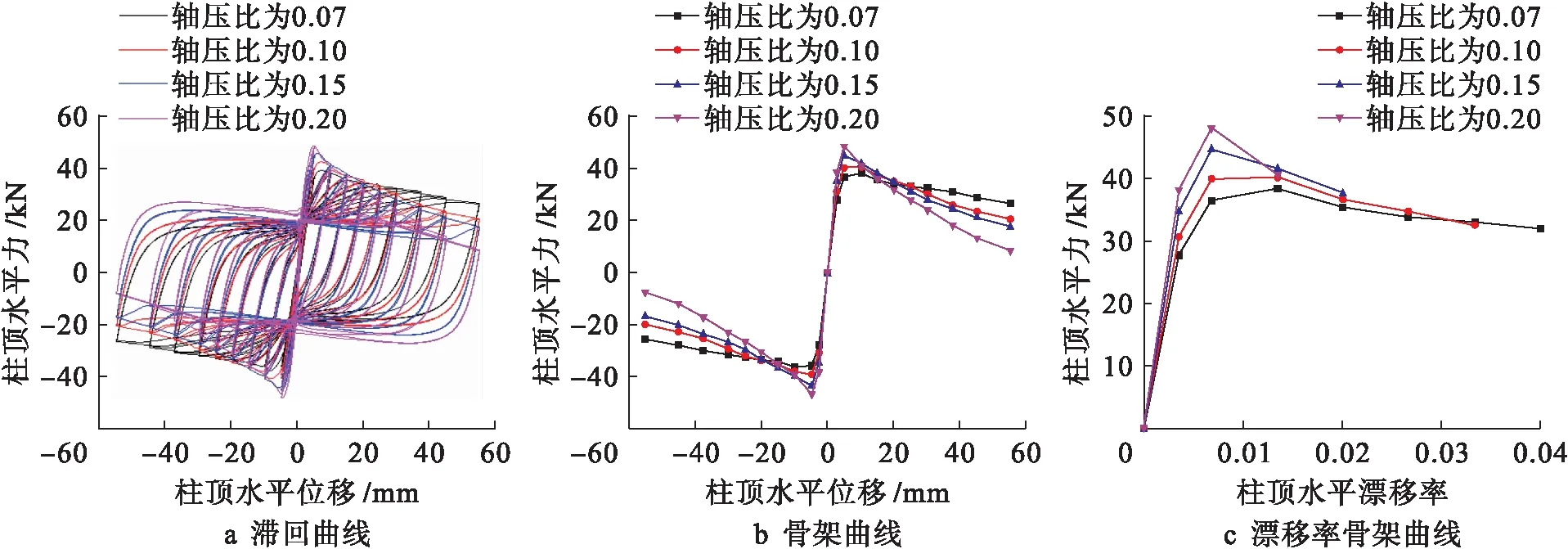
圖6 配箍率1.5%柱模擬數據Fig.6 Simulation data of column with stirrup ratio of 1.5%

圖7 配箍率2.1%柱模擬數據Fig.7 Simulation data of column with stirrup ratio of 2.1%
軸壓比的提高可增大柱的極限承載能力.在軸壓比為0.07、0.10時,框架柱達到峰值點荷載后,骨架曲線下降段斜率較為平緩,柱頂水平漂移率達到4%~6%,表現出了良好的延性能力.即使當荷載下降到承載能力的80%時,骨架曲線下降段依舊較為平緩,構件仍然具有一定的承載能力.
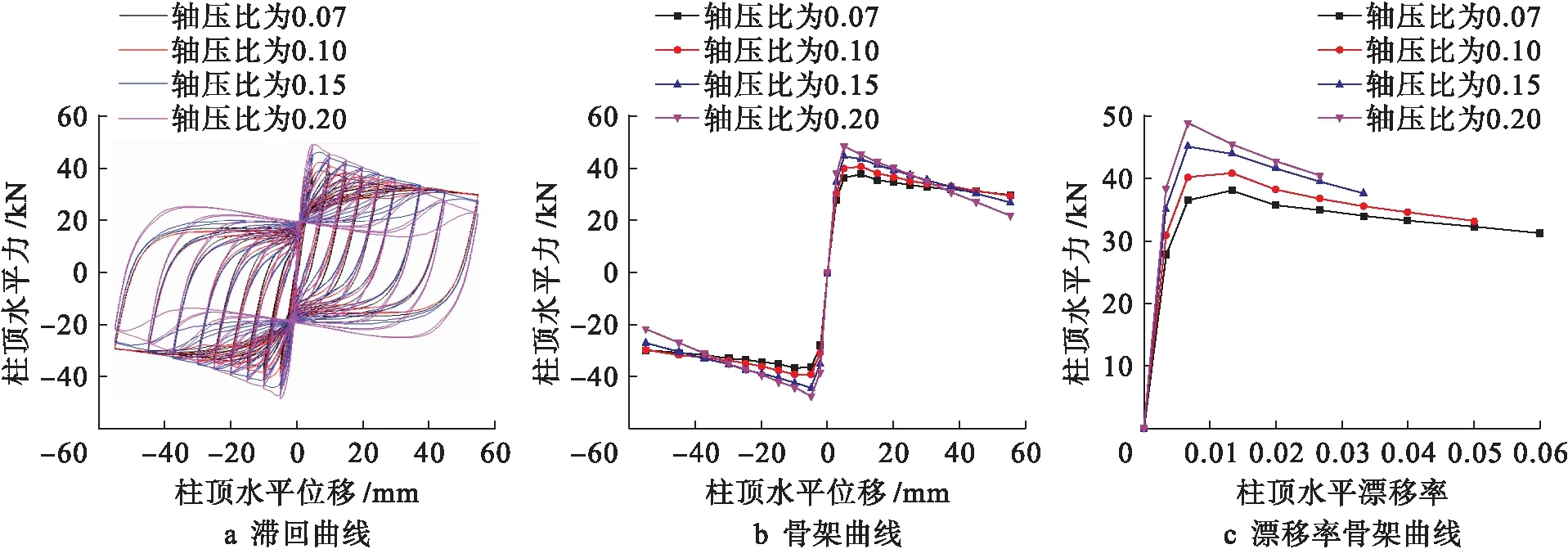
圖8 配箍率3.5%柱模擬數據Fig.8 Simulation data of column with stirrup ratio of 3.5%
但當軸壓比大于0.10時,P-Δ效應加劇,骨架曲線下降段越來越陡,斜率明顯變大,構件剛度急劇下降,柱頂水平漂移率也急劇下降,延性能力不足.
從上述三種配箍率分別對應的骨架曲線可以看出,構件配箍率的增大可提高構件的極限承載能力,在軸壓比為0.2時,荷載達到峰值點荷載后,配箍率為1.5%、2.1%的骨架曲線下降段急劇下降,未達到施加的最大強制位移時,構件已完全破壞;配箍率為3.5%的骨架曲線相較前兩種配箍率對應的骨架曲線下降段較為平緩,在完成施加的最大強制位移之前,構件剛度未出現陡降的情況.同時,從柱頂水平漂移率曲線可以看出,構件配箍率的增大,可增加柱頂水平漂移率值.在軸壓比為0.10時,三種配箍率框架柱分別對應的柱頂水平漂移率值為3.3%、4.0%和5.0%,故配箍率的增加可提高構件的極限承載能力和延性能力,同時在大軸壓比下,構件的配箍率應適當提高.
4 結 論
本文基于OpenSEES有限元軟件,采用非線性纖維單元對文獻[4]中4根以彎曲破壞為主、軸壓比處于0.09~0.20之間的鋼筋混凝土柱擬靜力試驗進行數值模擬,得出以下結論:
1) 采用OpenSEES中非線性纖維單元,利用Concrete02混凝土模型和Steel02鋼筋模型建立的非線性纖維單元數值模型,可高效、準確地模擬鋼筋混凝土柱擬靜力試驗.
2) 數值模擬與試驗數據對比表明,墩柱擬靜力試驗數值模擬分析應考慮P-Δ效應;鋼筋強化系數可不考慮或僅需設置0~0.01的較小強化系數值;Concrete02混凝土模型中的λ參數設置建議取0.1~0.2.
3) 通過不同軸壓比的鋼筋混凝土柱的擬靜力數值模擬分析得出:小軸壓比的鋼筋混凝土柱抗震性能較好,具有良好的延性能力.
4) 配箍率的增加可提高鋼筋混凝土柱的極限承載能力和延性能力,但在大軸壓比條件下,構件的配箍率應適當提高.

