基于SOA-MGM(1，n，q)模型的信息流通量預測*

羅朝輝， 黃激珊， 陳 昆

(興義民族師范學院 數學科學學院， 貴州 興義 562400)

隨著高等教育事業的發展，高等學校招生人數有了極大程度的增加，因此對高等教育資源的合理預測，對高等教育資源的合理調度和配置具有重要意義.對高校圖書館圖書信息流通量的定量研究和預測，對優化館藏、合理布置借閱空間、實現圖書借閱服務的科學管理及提高圖書利用率具有重要意義.

灰色模型最早由鄧聚龍教授提出，經過幾十年的發展，該理論被廣泛地應用于科學研究和工程應用，然而灰色模型的參數選擇直接影響預測效果和預測精度[1].為了提高灰色模型的預測精度，許多學者對灰色模型進行了改進和優化.文獻[2]將緩沖算子引入灰色模型，通過緩沖算子預處理原始數據，實現系統擾動對預測結果影響的消除；文獻[3]將信息差異法引入灰色模型，構建出指數算子、平移算子的模型，并對研究對象進行數據挖掘，該改進方法可以更好地挖掘數據的內在規律；文獻[4]運用遺傳算法進行灰色模型背景值最優參數的選擇，使得背景值的計算效果更加符合實際；文獻[5]應用粒子群算法對灰色模型的內在控制參數和發展系數進行最優選擇，從而實現該預測模型的參數自適應選擇和預測結果的最優化.人群搜索算法具有控制參數少、算法簡單和尋優速度快的優點，目前尚未發現該算法應用于灰色模型優化的文獻.本文將SOA算法和多變量灰色模型結合起來，提出一種基于SOA優化MGM(1，n，q)模型參數的預測模型，并將模型應用于高校圖書館圖書信息流通量更高精度的定量預測，在克服GM(1，1)、MGM(1，n)模型缺點的同時，提高了灰色模型的預測精度.

1 多變量灰色模型

1.1 GM(1，1)預測模型

灰色模型GM(1，1)的算法原理如下：設時間序列x(0)有n個觀測值，x(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}，通過累加生成新序列x(1)={x(1)(1)，x(1)(2)，…，x(1)(n)}，生成序列x(1)所對應的1階微分方程式為

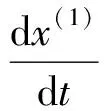
(1)

式中：u為內生控制灰數；a為發展系數.

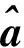
(2)

式中：

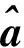
(3)

則GM(1，1)模型的時間響應序列可表示為

(4)

式(4)為GM(1，1)模型的預測方程，通過一次累減，預測方程可表示為

(i=0，1，2，…，n-1)

(5)

1.2 多變量MGM(1，n)模型

灰色GM(1，1)模型只能用于單一的時間序列數據，不能反映多個變量之間的相互影響，而GM(1，n)模型不用于預測，主要描述變量間的相互關系.本文將灰色GM(1，1)模型和GM(1，n)模型結合起來形成MGM(1，n)模型，該模型是GM(1，1)模型在n元變量情況下的擴展，由n元1階常微分方程組構成，GM(1，n)模型[6]表示為

則GM(1，n)模型矩陣表達形式為

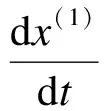
(6)

式中：M為內生控制參數矩陣；N為發展系數矩陣.連續時間響應函數[7]為

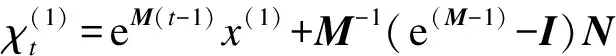
(7)

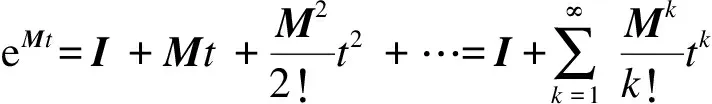
1.3 MGM(1，n，q)模型

針對式(6)進行向前差分和向后差分處理，MGM(1，n)的一般差分可表示為

(8)

由式(8)建立MGM(1，n，q)數學模型，對于任意q0，數據矩陣[8-9]有

(9)

(10)

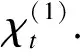
2 人群搜索算法

2.1 SOA算法基本思想

SOA算法是受人隨機搜索行為啟發而提出的智能搜索算法，該算法通過社會學習和認知學習獲取社會經驗和認知經驗，在結合智能群體的自組織聚集行為、以自我為中心的利己主義行為和人的預動行為基礎上，確定個體搜索方向，達到搜索尋優的目的[10-11].

2.2 SOA算法步驟

SOA算法的流程如下：

1)t→0.

2) 算法初始化，隨機產生m初始位置：{xi(t)|xi(t)=(xi1，xi2，…，xim)}.

3) 評價和計算每個位置的目標函數值.

4) 搜尋策略，計算每個個體i在每一維j的搜索方向dij(t)和步長cij(t).

搜索方向dij(t)由人的利己行為、利他行為和預動行為決定，任意第i個搜索個體的利己方向di，ego、利他方向di，alt和預動方向di，pro更新表達式為

di，ego(t)=pi，best-xi(t)

(11)

di，alt(t)=gi，best-xi(t)

(12)

di，pro(t)=xi(t1)-xi(t2)

(13)

式中：xi(t1)，xi(t2)分別為xi(t-2)，xi(t-1)的最佳位置；gi，best為第i個搜索個體所在鄰域的集體歷史最佳位置；pi，best為第i個搜索個體到目前為止經歷過的最佳位置.通過三個方向隨機加權幾何平均確定最終的搜索方向，其搜索方向更新表達式為

dij(t)=sign(ωdij，pro+φ1dij，ego+φ2dij，alt)

(14)

式中：φ1，φ2為[0，1]之間的常數；ω為慣性權值.

5) 對每個搜尋者位置進行更新，更新表達式為

xij(t+1)=xij(t)+Δxij(t+1)

(15)

Δxij(t+1)=αij(t)dij(t)

(16)

6)t→t+1.

7) 若算法終止條件滿足，算法終止；反之，則轉到步驟3).

3 基于SOA優化MGM(1，n，q)模型

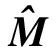
4 實驗分析

4.1 數據來源

為了驗證本文算法的有效性和可靠性，以某高等教育學校2000～2012年的圖書館實際統計流通量為研究對象進行實驗，具體數據如表1所示.

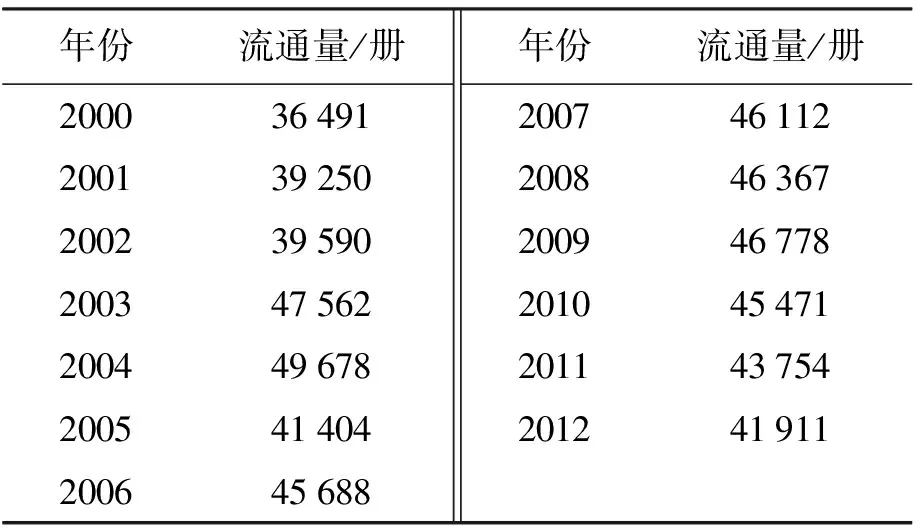
表1 某高等教育學校2000～2012年圖書館信息流通量Tab.1 Information capacity of library from 2000 to2012 for a higher education university

4.2 評價指標

為了評價預測效果，選擇平均絕對百分比誤差和均方根誤差作為評價指標，兩項指標的計算表達式為

(17)

(18)

4.3 實驗結果

為驗證本文算法的有效性，將SOA-MGM(1，n，q)與MGM(1，n)、GM(1，1)三種算法進行對比.

設定種群規模sizepop=100，最大迭代次數iteration=100，最大隸屬度值Umax=0.950 0，最小隸屬度值Umin=0.011 1，權重最大值Wmax=0.9，權重最小值Wmin=0.1，MGM(1，n，q)和GM(1，n)的控制參數n=2，三個數學模型的圖書館借閱信息流通量預測結果分別如圖1～3所示.預測誤差圖(包括絕對誤差和相對誤差)如圖4所示.

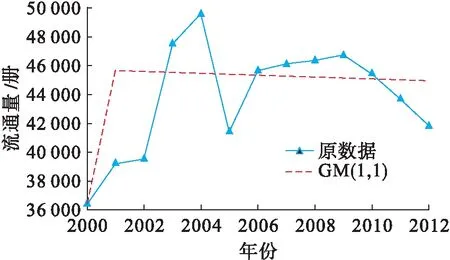
圖1 GM(1，1)預測結果Fig.1 Prediction results of GM(1，1)

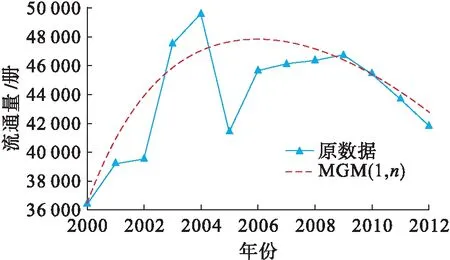
圖2 MGM(1，n)預測結果Fig.2 Prediction results of MGM(1，n)

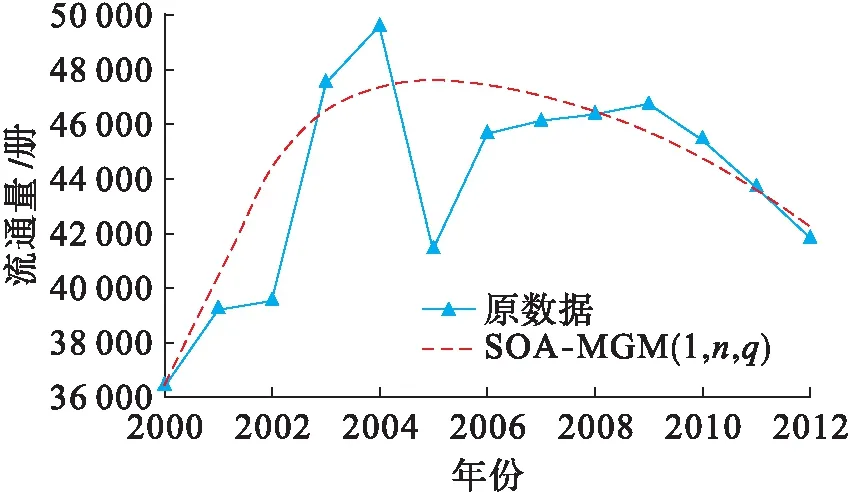
圖3 SOA-MGM(1，n，q)預測結果Fig.3 Prediction results of SOA-MGM(1，n，q)

由圖4a預測絕對誤差對比圖可知，SOA-MGM(1，n，q)的預測絕對誤差低于MGM(1，n)和GM(1，1)；由圖4b預測相對誤差對比圖可知，SOA-MGM(1，n，q)的預測相對誤差低于MGM(1，n)和GM(1，1)，從而說明本文算法的優越性，具有更高精度.圖5為SOA算法對MGM(1，n，q)進行參數尋優的收斂圖.不同算法的評價指標對比結果表2所示.

由表2可知，在RMSE和MAPE二個評價指標中，SOA-MGM(1，n，q)的預測精度最高，優于MGM(1，n)和GM(1，1)；其次，MGM(1，n)的預測精度優于GM(1，1)；GM(1，1)的預測精度最差，RMSE和MAPE分別比SOA-MGM(1，n，q)高5.02和4.64%.由此看出，本文提出的方法其預測效果較好，提高了預測精度.

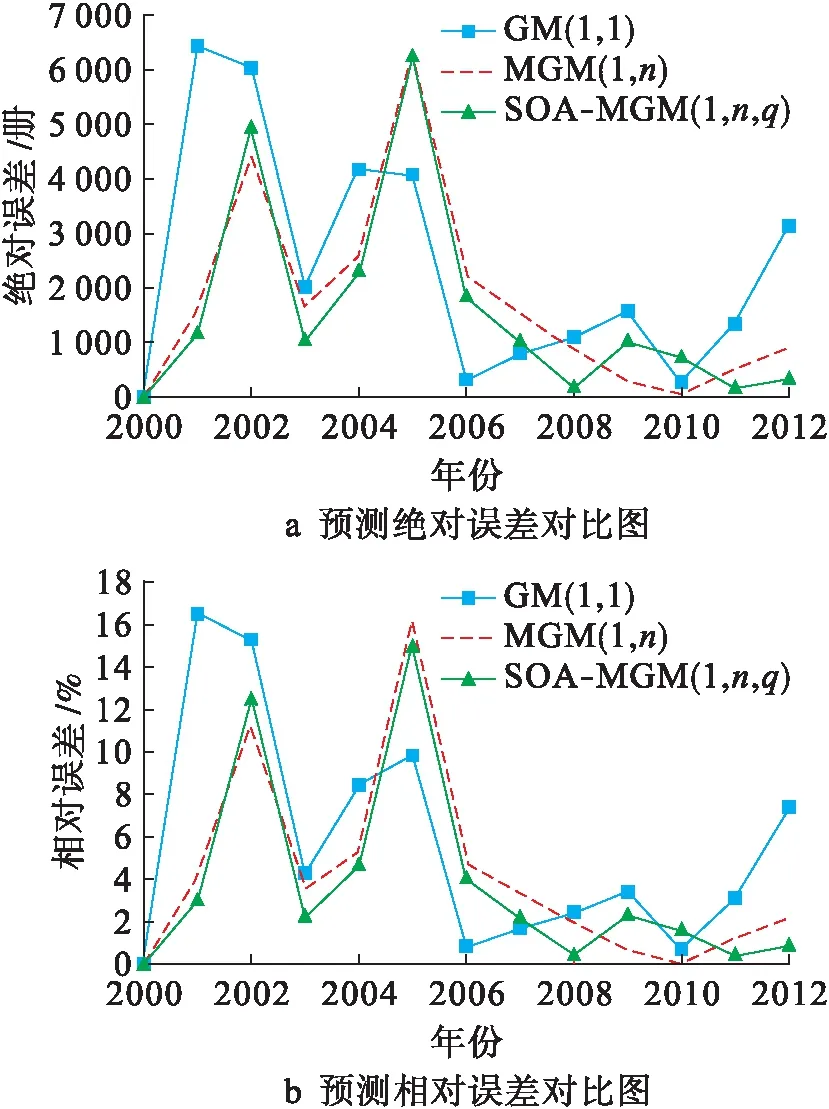
圖4 預測誤差圖Fig.4 Prediction error

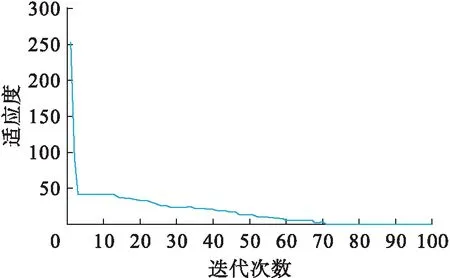
圖5 SOA-MGM(1，n，q)適應度曲線圖Fig.5 Fitness curve of SOA-MGM(1，n，q)

方法RMSEMAPE/%SOA-MGM(1,n,q)3.215.11MGM(1,n)4.375.98GM(1,1)8.239.75

5 結 論

針對傳統GM(1，1)模型和MGM(1，n)模型存在不同的缺點，本文將GM(1，1)模型和MGM(1，n)模型結合起來，運用SOA算法對模型MGM(1，n，q)的參數q進行尋優求解以獲得最優參數q0.本文以某高等教育學校2000～2012年圖書館實際統計流通量為研究對象進行實驗，實驗結果表明，與MGM(1，n)和GM(1，1)方法相比，本文算法模型可以提高預測精度和預測效果，從而為圖書館借閱信息流量的控制和圖書借閱策略的優化提供了科學合理的決策依據.