基于雙線性映射的支持全操作的公共可驗證外包數據庫模型
王 強 周福才 玄鵬開 吳淇毓
(東北大學軟件學院 沈陽 110169) (wangq3635@126.com)
隨著云計算的發展,數據庫外包服務[1]成為近些年新興的一種應用模式.越來越多資源受限的客戶或企業為了節約硬件存儲資源和管理成本,取消自己的數據中心,將數據庫外包給專業的數據庫服務提供商[2]進行管理和維護.但是數據外包后,數據擁有者喪失了對數據的直接控制[3],云服務器可能會篡改數據庫的內容或偽造查詢結果來減少響應的時間和計算代價,因此研究外包數據庫查詢結果的完整性問題具有重要意義.
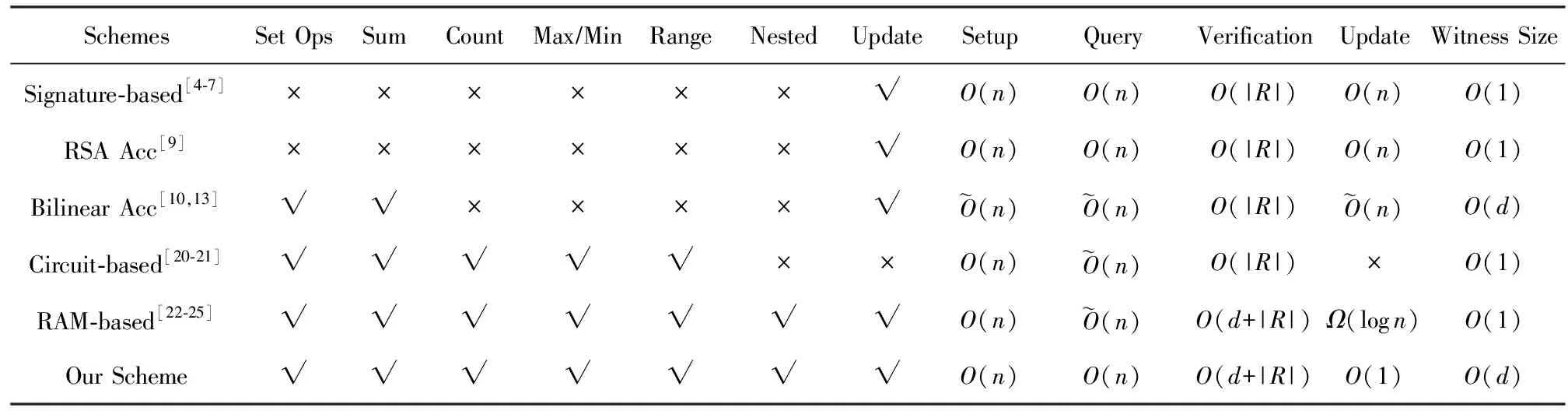
目前,為解決外包數據庫的查詢結果完整性驗證問題,國內外學者展開了大量的研究,主要分為3類:基于數字簽名的[4-7]、基于認證數據結構的[8-16]、基于可驗證計算的[17-25].1)使用數字簽名技術的方法[4-7]中,數據擁有者需要對外包數據庫中的每個元組進行簽名,客戶查詢時,服務器需返回查詢結果和查詢結果中每個元組所對應的簽名.但是該類方法存在的問題是驗證和更新的代價較高,且只支持范圍查詢.2)基于認證數據結構的方法是對基于數字簽名方法的改進,通常是基于認證樹和累加器的.基于認證樹[8,11-12,14-15]不需要對每一條元組進行簽名,而是先對元組排序,再使用Hash函數計算出樹中每個節點的Hash值,最終對樹的根節點簽名,客戶使用認證路徑和根節點簽名值進行驗證.但是該類方法存在的問題是由于葉子節點是排序好的元組的Hash值,任何一次更新都可能破壞已有認證數據結構,更新代價較高.認證路徑隨元組的數量呈對數級增長,只支持范圍和元素隸屬關系的查詢.另一種基于累加器的[9-10,13],只支持集合交集、并集、差集及元素隸屬關系的查詢,不支持求和、計數、范圍,最大值和最小值查詢.此外,文獻[16]提出了一種基于可翻轉的布隆過濾器的外包數據庫驗證方案,該方案雖解決了數據更新操作時額外的計算開銷,但布隆過濾器存在誤算率,會導致查詢結果的精準性.3)基于可驗證計算的方法分為2類:①針對特定查詢類型的[17-19];②針對通用方案的[20-25].前者的效率優于后者,但是查詢類型單一.例如Papadopoulos等人[19]基于雙線性映射累加器提出了支持多維范圍查詢的完整性驗證的方案,該方案只支持多維范圍查詢且不支持高效地更新數據.針對通用方案的可分為2類:基于電路的[20-21]和基于RAM(random access memory)模型的[22-25].兩者均是將外包庫編譯到程序中(表示成一個布爾/算數電路,或者是基于RAM模型進行計算),在編譯好的程序中輸入查詢語句,返回與之對應的結果.這2種方法計算代價高并不實用.基于電路的方法效率低,程序中電路的大小至少與數據庫本身一樣大,不支持嵌套查詢,每進行更新操作都需要重新編碼.基于RAM模型支持全部查詢操作,但是編碼難度較高和性能較差.
綜上所述,現有的方案存在的問題:1)查詢類型單一不支持全操作;2)證據隨查詢結果呈線性或對數增長;3)驗證和更新代價較高;4)方案的整體效率低下難以應用.
針對上述問題,本文提出了一個基于雙線性映射的支持全操作的公共可驗證外包數據庫(publicly verifiable database model with full operations based on bilinear map, BMPVDB)模型,該模型具有3個特點:
1) 功能全面(全操作).該模型支持的查詢操作全面,包含了交集、并集、補集等各種集合操作,求和、計數、最小值、最大值、范圍查詢以及嵌套查詢操作.
2) 高效.驗證代價為常數級,獨立于外包數據庫的大小和查詢的中間結果.證據大小只依賴于查詢語句分解為單個查詢語句的數量,不依賴于外包數據庫和中間結果的大小.更新的代價為常數級,不依賴于外包數據庫和中間結果的大小.
3) 公共可驗證、公共可更新.任何客戶擁有公鑰和摘要都能對查詢結果進行完整性驗證.任何一個被數據擁有者授權的客戶無需私鑰參與就能對外包的數據進行更新.
1 相關知識
1.1 雙線性映射
雙線性映射指的是2個循環群之間相對應的線性映射關系.定義一個概率多項式時間雙線性映射生成算法(e,g,G,GT,p)←BMGen(1λ)生成雙線性映射e:G×G→GT,其中p為λ比特的素數,G和GT均為p階乘法循環群,g為群G的生成元,雙線性映射e滿足3個性質:
1) 雙線性.對于任意的a,b∈p和P,Q∈G,均滿足e(Pa,Qb)=e(P,Q)ab.
2) 非退化性.e(g,g)≠1GT,其中1GT為群GT的單位元.
3) 可計算性.對于任意的P,Q∈G,都存在有效的算法計算出e(P,Q).
雙線性映射可通過超奇異橢圓曲線上的Weil和Tate配對來進行構造.
1.2 多項式分解定理
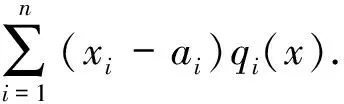
1.3 泰勒展開式
若函數f(x)在包含x0的某個閉區間[a,b]上具有n階導數,且在開區間(a,b)上具有(n+1)階導數,則對閉區間[a,b]上任意一點x,均有:
其中,f(i)(x)為f(x)的i階導數,Rn(x)為泰勒公式的余項,是(x-x0)n的高階無窮小.
1.4 雙線性q -階強判定性Diffie-Hellman假設[26]
雙線性q-階強判定性Diffie-Hellman困難性假設(bilinearq-strong Diffie-Hellman,q-BSDH),給定(e,g,G,GT,p)←BMGen(1λ)和q元組(gα,…,gαq),不存在一個概率多項式算法A能以不可忽略的概率輸出(c,h),使得h=e(g,g)(α+c)-1.其形式化定義為
其中,neg(λ)為可忽略函數.
1.5 變體的雙線性Diffie-Hellman指數假設[27]
變體的雙線性Diffie-Hellman指數困難性假設(variant of bilinear Diffie-Hellman exponent, VBDHE),給定(e,g,G,GT,p)←BMGen(1λ),gαi(i∈[1,q])和gβiαj((i,j)∈[1,q]×[1,q]),不存在一個概率多項式算法A能以不可忽略的概率輸出(G(·),h),使得h=e(g,g)G(α)βq.其形式化定義為
其中,neg(λ)為可忽略函數.
2 BMPVDB模型
本節主要介紹了基于雙線性映射的支持全操作的公共可驗證外包數據庫BMPVDB模型.首先給出了模型的架構及交互流程,然后對模型進行了形式化定義,最后針對模型應滿足的不同安全需求給出了安全性定義.
2.1 BMPVDB模型的架構
BMPVDB模型中包含數據擁有者、客戶、云服務器3方實體,其中數據擁有者和客戶是可信的,云服務器是不可信的.其模型架構圖如圖1所示:
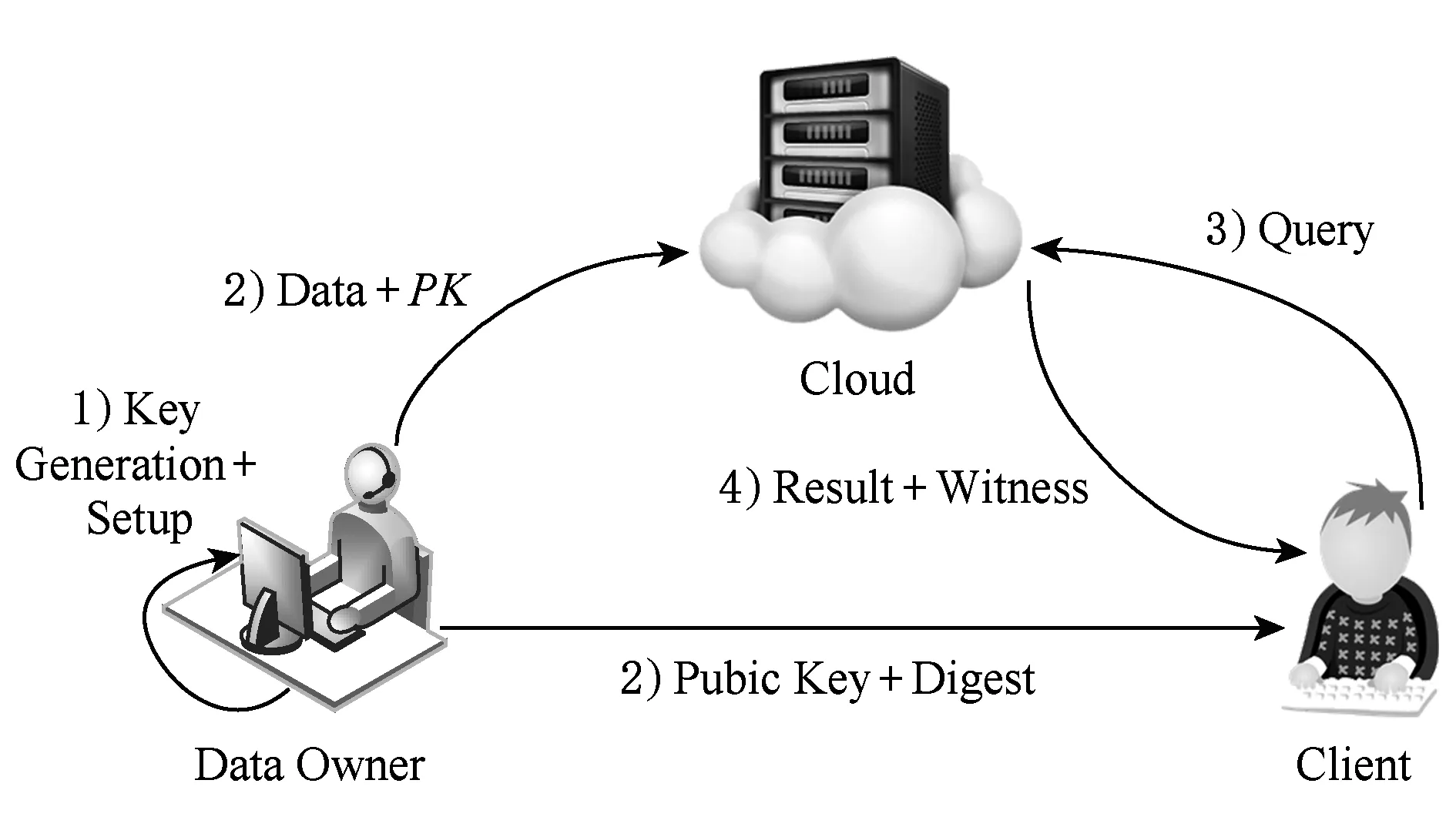
Fig. 1 The architecture of BMPVDB圖1 BMPVDB方案的架構
數據擁有者首先執行密鑰生成算法生成公私鑰對,其中公鑰主要用于生成和驗證證據,私鑰主要用于對外包數據庫的更新.然后執行初始化算法生成外包數據庫摘要.將數據庫外包到云服務器進行存儲和管理,同時將公鑰發送給云服務器.然后將公鑰和摘要發送給客戶.當客戶向云服務器發起查詢請求后,云服務器返回查詢的結果和證據.客戶利用本地儲存的公鑰、摘要及云服務器返回的證據對結果進行驗證.該模型中云服務是不可信的,可能篡改查詢的結果.為保證查詢結果的完整性,云服務器在返回查詢結果的同時,還將返回相應的證據供客戶驗證.驗證時涉及公鑰和摘要,且均為公開的,因此該方案支持公共可驗證,即擁有公鑰的客戶都可對查詢的結果進行驗證.
2.2 BMPVDB的形式化定義
該模型可用五元組表示為{KeyGen,Setup,Query,Verify,Update},五元組中每個元組都代表一個多項式時間算法.5個算法具體描述如下:
1) 密鑰生成算法(PK,SK)←KeyGen(1λ).輸入安全參數λ,數據擁有者執行該算法生成公私鑰對(PK,SK).其中私鑰SK被數據擁有者私密保存,公鑰PK被公開.
2) 初始化算法σDB←Setup(PK,DB).數據擁有者將公鑰PK和外包數據庫DB作為輸入,調用該算法得到數據庫摘要σDB,最后公開σDB.
3) 查詢算法(R,π)←Query(Q,PK,DB).云服務器將公鑰PK,外包數據庫DB和客戶給定的查詢Q輸入至該算法,算法輸出查詢的結果R及證據π.
4) 驗證算法{‘1’ or ‘0’}←Verify(PK,σDB,R,π).客戶對云服務器返回的結果進行驗證.算法輸出‘1’表示驗證通過,接受查詢結果R,否則輸出‘0’,拒絕查詢結果R.
2.3 BMPVDB的正確性及安全性定義
2.3.1 正確性
模型的正確性簡單來說,當模型中每個算法都正確執行,驗證算法Verify始終輸出‘1’,即永遠不會拒絕一個正確的查詢結果.其形式化定義為
其中,neg(λ)為可忽略函數.
2.3.2 安全性
模型的安全性是針對不可信云服務器來說的.簡單來說,云服務器偽造一個惡意的結果和證據始終不能通過驗證.下面通過構造敵手A和挑戰者C之間的安全性實驗∑來定義該模型的安全性.
對于任意的查詢Q,敵手A試圖通過4個步驟來偽造一個查詢結果和證據并通過驗證:
1) 給定安全參數λ,C執行算法KeyGen生成公私鑰對(PK,SK),并將PK發送給A,私鑰SK私密保留.
2) 敵手A選定一個外包數據庫DB,并將DB發送給挑戰者C.
3) 挑戰者C在接收到DB后,執行算法Setup,生成外包數據庫DB的摘要σDB.
4) 敵手A可向挑戰者C發起多項式poly(λ)次更新與查詢:
更新.A選定更新操作upd,將upd發送給C.C
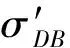
查詢.A對于查詢Q偽造一個結果R*和證據π*.如果算法Verify(PK,σDB,R*,π*)輸出‘1’,敵手獲勝.
對于任意一個概率多項式時間的敵手A,如果A在上述安全性實驗∑中獲勝的概率是可忽略的,則稱BMPVDB是安全的.
3 BMPVDB模型的實施方案
本節主要介紹了基于雙線性映射的支持全操作的公共可驗證外包數據庫BMPVDB模型的實施方案.首先給出了該模型實施方案的總體描述及核心思想,然后給出了該模型實施方案中各算法的詳細設計,并給出了安全性證明.最后給出了該模型實施方案的擴展及應用.
3.1 BMPVDB模型實施方案的總體描述
對數據庫任意查詢操作都可看成對表中行或列的操作,而數據庫表中每行或每列所包含的元素均可看作一個集合,因此對數據庫的查詢就相當于對集合的操作.從查詢輸入和輸出的類型可以將查詢分成5類:
1) 輸入2個集合輸出1個集合,該類型的查詢對應于交集∩、并集∪、差集和對稱差集Δ.
2) 輸入輸出均為一個集合,該類型的查詢對應于補集和范圍查詢RANGE.
3) 輸入一個集合輸出一個整數,該類型的查詢包含最大值MAX、最小值MIN、計數COUNT和求和SUM.
4) 輸入一個集合輸出為一個布爾值,該類型的查詢包含了屬于∈x和不屬于?x.
5) 嵌套查詢,該類型查詢是上述4種類型查詢的自由組合.
在本方案中類型1和類型2中所包含的查詢均可通過交集查詢來實現(詳見3.2節),范圍查詢可通過最大值,最小值和集合操作來實現詳見(詳見3.2節),嵌套查詢可通過復合上述4種類型查詢來實現詳見(詳見3.2節),下面將重點介紹集合交集、最大值、最小值、求和、計數.
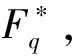
(α1+α2+α3)(β2αq-2+β3αq-3+β4αq-4)=
(β2αq-1+β3αq-2+β4αq-3)+(β2αq+β3αq-1+
β4αq-2)+(β2αq+1+β3αq+β4αq-1)=
(β2+β3)αq+Q(β,α).
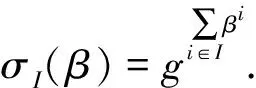
3.2 BMPVDB模型實施方案的詳細設計及安全性證明
本節首先詳細介紹了基于雙線性映射的支持全操作的公共可驗證外包數據庫方案中密鑰生成算法,初始化算法和更新算法.然后給出了不同查詢類型下的查詢算法與驗證算法的具體構造,并進行了安全性證明.下面分別對其進行描述.
1) 密鑰生成算法(PK,SK)←KeyGen(1λ).該算法用于生成公私鑰對(PK,SK).算法的主要步驟為:
② 給定安全參數λ,調用算法BMGen生成(e,g,G,GT,p).
③ 對于所有的i,j∈q,計算gαi和gβiαj,其中q=poly(λ).
④ 將(e,g,G,GT,p),gαi(i∈[1,q])和gβiαj((i,j)∈[1,q]×[1,q])當作公鑰PK.
⑤ 輸出(PK,SK).
2) 初始化算法σX←Setup(PK,X).該算法主要用于計算集合X的摘要.算法主要步驟為:
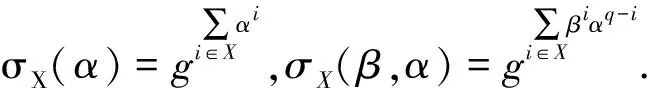
② 輸出集合X的摘要σX=(σX(α),σX(β,α)).
4) 查詢與驗證算法
查詢算法用于返回查詢的結果和證據.驗證算法用于驗證查詢結果的正確性.
① 交集I=X∩Y
查詢:
(i) 計算出集合X,Y交集的結果I.
(ii) 根據集合X,I和Y中元素,求得多項式
(iii) 求得多項式
Q(y,x)=X (x)Y(y,x)-I(y)xq.
(iv) 根據公鑰PK,計算出證據π=(gI(β),gQ(β,α)),返回I和π.說明:如果證據π中包含2個元素,則令π=(π[0],π[1]).
驗證:
(ii) 根據公鑰PK,σX(α),σY(β,α)和證據π來驗證下列等式是否成立:
e(σX(α),σY(β,α))=e(π[0],gαq)e(π[1],g).
(iii) 如果等式成立,則接受交集查詢的結果I,輸出‘1’,否則拒絕結果I,輸出‘0’.
安全性證明見定理1:
定理1. 如果在概率多項式時間內存在一個敵手A能以不可忽略的概率偽造出錯誤的結果I*和證據π*=(g∑aiβi,g∑bi,jαiβj)通過驗證(即贏得安全性實驗∑),那么任意一個敵手A能找到一個有效的算法B解決VBDHE難題和q-BSDH難題.
證明. 因為A偽造的結果及證據通過驗證,則有:
e(σX(α),σY(β,α))=e(π*[0],gαq)e(π*[1],g),
(1)
對于正確的結果和證據,則有:
e(σX(α),σY(β,α))=e(π[0],gαq)e(π[1],g).
(2)
由式(1)和式(2)可得:
e(π[0],gαq)e(π[1],g)=
e(π*[0],gαq)e(π*[1],g)?
e(π[0],gαq)e(π[1],g)=
e(g∑aiβi,gαq)e(g∑bi,jαiβj,g)?
gI(β)αq+Q(β,α)=g(∑aiβi)αq+∑bi,jαiβj?
g(I(β)-∑aiβi)αq=g∑bi,jαiβj-Q(β,α).
令G(β)=I(β)-∑aiβi,如果I(β)≠∑aiβi,可求得gG(β)αq=g∑bi,jαiβj-Q(β,α),因此A可找到有效的算法B解決VBDHE問題.又因為該問題是難解的,所以I(β)≠∑aiβi不成立,故有π*[0]=π[0]且I≠I*.令xmin為I∪I*中最小元素,因為π*[0]=π[0],所以:
(3)
式(3)右邊提供了有效的算法B解決q-BSDH問題.又因為該問題是難解的,所以π*[0]=π[0]且I ≠I*不成立.
綜上,在概率多項式時間內A難以以不可忽略的概率贏得安全性實驗∑,因此該方案是安全的.
證畢.
② 其他集合操作
集合的其他操作可通過交集來實現[28],其查詢算法,驗證算法和安全性證明均與交集相似,這里將不在贅述,只給出驗證查詢結果正確性的等式.
σZ(α)=σX(α)σY(α)σI(α).
(ii) 差集D=XY(D=X∩I),驗證等式:
σD(α)=σX(α)σI(α).
(iii) 對稱補集S=XΔY(S=XI)∪(YI),驗證等式:
σS(α)=σX(α)σY(α)σI(α)2.
(v) 子集X?Y(X =X∩Y),驗證等式:
σX(α)=σI(α).
(vi) 屬于x∈X ({x}=X∩(x)),驗證等式:
σI(α)=gαx.
(vii) 不屬于x?X (?=X∩(x)),驗證等式:
σI(α)=1.
③ 計數count(X)
查詢:
(iii) 根據多項式分解定理(詳見1.2節),計算出多項式Q(x)=(X (x)-X (1))(x-1).
(iv) 根據公鑰PK,計算出證據π=gQ(α),并返回R和π.
驗證:
(i) 利用查詢返回的結果R,計算gR.
(ii) 根據公鑰PK,σX(α)和證據π來驗證下列等式是否成立:
e(σX(α),g)=e(g,gR)e(π,gα-1).
(iii) 如果等式成立,則接受交集查詢的結果R,輸出‘1’,否則拒絕結果R,輸出‘0’.
安全性證明見定理2:
定理2. 如果在概率多項式時間內存在一個敵手A能以不可忽略的概率偽造出錯誤的結果R*和證據π*通過驗證(即贏得安全性實驗∑),那么任意一個敵手A能找到一個有效的算法B解決q-BSDH難題.
證明. 因為A偽造的結果及證據通過驗證,則有:
e(σX(α),g)=e(g,gR*)e(π*,gα-1)=
e(g,gR*)e(gQ*(α),gα-1),
(4)
對于正確的結果和證據,則有:
e(σX(α),g)=e(g,gR)e(π,gα-1)=
e(g,gR)e(gQ(α),gα-1).
(5)
由式(4)和式(5)可得:
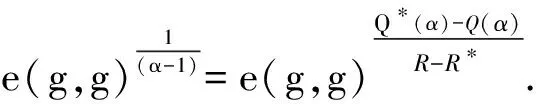
(6)
式(6)右邊提供了有效的算法B解決q-BSDH問題.又因為該問題是難解的,所以在概率多項式時間內A難以以不可忽略的概率贏得安全性實驗∑,因此該方案是安全的.
證畢.
④ 求和sum(X)
查詢:
(iii) 計算X (1),根據泰勒展開式(詳見1.3節,其中n=2),計算出多項式Q(x)=(X (x)-X (1)-X′(1)(x-1))(x-1)2.
(iv) 根據公鑰PK,計算出gQ(α),將(X (1),gQ(α))作為證據π,返回R和π.
驗證:
(i) 利用查詢返回的結果R,計算gR.
(ii) 根據公鑰PK,σX(α)和證據π來驗證下列等式是否成立:
e(σX(α),g)=
e(gπ[0],g)e(gR,g(α-1))e(π[1],g(α-1)2).
(iii) 如果等式成立,則接受交集查詢的結果R,輸出‘1’,否則拒絕結果R,輸出‘0’.
安全性證明見定理3:
定理3. 如果在概率多項式時間內存在一個敵手A能以不可忽略的概率偽造出錯誤的結果R*和證據π*通過驗證(即贏得安全性實驗∑),那么任意一個敵手A能找到一個有效的算法B解決q-BSDH難題.
證明. 因為A偽造的結果及證據通過驗證,則有:
e(σX(α),g)=
e(gπ*[0],g)e(gR*,g(α-1))e(π*[1],g(α-1)2)=
e(gπ*[0]+R*(α-1),g)e(π*[1],g(α-1)2),
(7)
對于正確的結果和證據,則有:
e(σX(α),g)=
e(gπ[0],g)e(gR,g(α-1))e(π[1],g(α-1)2)=
e(gπ[0]+R(α-1),g)e(π[1],g(α-1)2).
(8)
由式(7)和式(8)可得:
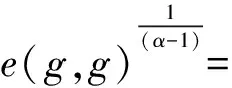
上式右邊提供了有效的算法B解決q-BSDH問題.又因為該問題是難解的,所以在概率多項式時間內A難以以不可忽略的概率贏得安全性實驗∑,因此該方案是安全的.
證畢.
⑤ 最小值min(X)
查詢:
(ii) 查看集合中最小元素或將多項式最小指數最為最小值查詢的結果R=min(X).
(iii) 根據公鑰PK,計算出證據π=g(X(α)-αR)αR+1,并返回R和π.
驗證:
(i) 根據公鑰PK,σX(α),證據π和結果R來驗證下列等式是否成立:
e(σX(α),g)=e(gαR,g)e(π,gαR+1).
(ii) 如果等式成立,則接受交集查詢的結果R,輸出‘1’,否則拒絕結果R,輸出‘0’.
安全性證明見定理4:
定理4. 如果在概率多項式時間內存在一個敵手A能以不可忽略的概率偽造出錯誤的結果R*和證據π*通過驗證(即贏得安全性實驗∑),那么任意一個敵手A能找到一個有效的算法B解決q-BSDH難題.
證明. 如果敵手A偽造的結果及證據通過驗證,則有:
e(σX(α),g)=e(gαR*,g)e(π,gαR*+1).
(9)
當R* e(gαR*,g)=e(σX(α),g)e(π*,gαR*+1)? (10) 當R*>R=min(X)時,定義U={i∈X:i (11) 因為U∩W=?,可得αR是U(α)和W(α)最大公因子,再由廣義歐幾里德定理可得,存在2個多項式a(α)和b(α),使得: 因此式(11)可得: 上式右邊提供了有效的算法B解決q-BSDH問題.又因為該問題是難解的,所以在概率多項式時間內A難以以不可忽略的概率贏得安全性實驗∑,因此該方案是安全的. 證畢. ⑥ 最大值max(X) 查詢: (i) 根據集合X中的元素,求得 (ii) 查看集合中最大元素或將多項式中關于y最大指數作為最大值查詢的結果R=max(X). (iii) 根據公鑰PK,計算出證據π=g(X(β,α)-βRαq-R)αq-R+1,并返回R和π. 驗證: (i) 根據公鑰PK,σX(α),證據π和結果R來驗證下列等式是否成立: e(σX(β,α),g)=e(gβRαq-R,g)e(π,gαq-R+1). (ii) 如果等式成立,則接受交集查詢的結果R,輸出‘1’,否則拒絕結果R,輸出‘0’. 最大值查詢的安全性證明與最小值查詢類似,因此不再贅述. ⑦ 范圍查詢range(l,r) 查詢: (i) 根據查詢范圍[l,r],將被查詢集合X分割成3個不相交集合U,V,W,其中U={i:i∈X,i (ii) 分別調用集合U∩V,U∩W和V∩W查詢算法返回對應的結果和證據. (iii) 分別調用集合U和W的最大值和最小值查詢算法返回對應的結果和證據. 驗證: (i) 分別調用集合U∩V,U∩W和V∩W驗證算法,若驗證失敗,輸出‘0’,否則,執行下一步. (ii) 分別調用集合U和W的最大值和最小值驗證算法,若驗證失敗,輸出‘0’,否則,執行下一步. (iii) 驗證max(U) 范圍查詢的安全性證明依賴于集合的交集、最大值和最小值查詢的安全性,上文已證,因此不再贅述. ⑧ 嵌套查詢 本方案是嵌套查詢,查詢時遞歸調用嵌套查詢中的每個查詢,但是無需返回中間的結果,只需返回中間結果的摘要和對應的證據.驗證時,同樣遞歸調用嵌套查詢中的每個查詢所對應的驗證算法,驗證查詢結果的正確性.該查詢的安全性依賴于上述各類查詢的安全性,因此該查詢也是安全的. Table1 Comparison with Prior Work表1 方案對比 Notes:√ means the scheme is applicable;× means the scheme is not applicable. 根據4.1節中方案的對比分析可知:基于簽名的可驗證外包數據庫方案無論在功能上還是性能上都低于其他2類方法;基于認證數據結構的方法中,雖然在部分方案與基于可驗證計算的方案中性能相近,但是前者所支持的操作遠小于基于可驗證計算方案所支持的操作.因此只與基于可驗證計算的方案相比較.而在基于可驗證計算的方案中,基于電路的方案所支持的查詢操作不及基于RAM的方案豐富,且基于RAM的方案中SNARK方案[25]較高效.因此在實驗分析中只與SNARK 方案進行對比.實驗中,主機的配置為Intel?CoreTMi7-4770 3.40 GHz主頻的處理器和32 GB內存,選定的安全參數λ=128,測試語句為嵌套查詢語句count((X∩Y)∪(U ∩W)),其中每個集合大小相等均為n.數據集利用偽隨機數生成器以時間戳為輸入隨機產生.每次執行時,數據集都不相同.保證了數據集的隨機可靠性和程序的健壯性.對本方案和SNARK方案中的初始化算法的效率、查詢算法的效率、驗證算法的效率、證據的大小和云服務器所需的存儲空間進行了測試、對比與分析. 兩方案中初始化算法的效率比較結果如圖2所示,橫坐標為集合的大小,縱坐標為該算法運行的時間.將本方案運行時間放大10 000倍,仍遠小于SNARK方案的運行時間.因此,在初始化算法上,雖然理論分析上兩方案相近,但本方案更高效. Fig. 2 Comparison for setup in time cost圖2 初始化算法運行時間比較 兩方案查詢算法的效率比較結果如圖3所示,將本方案運行時間放大100倍,仍小于SNARK方案的運行時間.因此,在查詢算法上,雖然理論分析上兩方案相同,但本方案更高效. Fig. 3 Comparison for query in time cost圖3 查詢算法運行時間比較 兩方案中驗證算法的效率比較結果如圖4示,兩方案中驗證效率均為常數級,不隨集合大小增加而增大,且本方案驗證效率小于SNARK方案.因此在驗證算法上,雖然理論分析上兩方案相近,但本方案更高效.在進行更新操作時,本方案在任意大小的數據下所消耗的時間大約為2.6 μs.由于SNARK對硬件要求較高,在現有的實驗條件內未測出SNARK更新操作所需的精準時間,但實驗表明了其所需時間要遠大于本方案所需時間.此外,4.1節理論分析可知,更新時,SNARK的效率為Ω(logn),本方案的效率為O(1)遠小于SNARK的效率.基于以上2點,本方案中更新算法的效率遠高于SNARK方案中更新算法的效率. Fig. 4 Comparison for verify in time cost圖4 驗證算法運行時間比較 兩方案中證據的大小比較結果如圖5所示,兩方案中證據的大小恒定不變,不隨集合大小的增加而增加,且本方案中證據的大小小于SNARK方案.因此在證據的大小上,雖然理論分析上兩方案相同,但本方案通信代價更低. Fig. 5 Comparison for witness size圖5 證據大小比較 兩方案中云服務器所需要的存儲空間比較結果如圖6所示,橫坐標為集合的大小,縱坐標為云服務器所需的存儲空間.將本方案所需的存儲空間放大10倍,仍小于SNARK方案.因此本方案的數據膨脹率更低. Fig. 6 Comparison for storage size圖6 存儲空間比較 以上實驗結果表明,本方案在初始化算法的效率、查詢算法的效率、驗證算法的效率、證據的大小及存儲空間上均優于SNARK方案.因此本方案效率更高、通信代價更小、數據膨脹率更低,更適合應用于實際. 針對現有可驗證外包數據方案存在查詢類型單一、效率低下、驗證和更新代價較高,難以應用于實際等問題,深入系統地研究了國內外關于可驗證外包數據庫相關方案,并總結各方案的優缺點.在此基礎上,基于雙線性映射提出了一個支持全操作的公共可驗證外包數據庫方案,給出了該方案的形式化定義,正確性及安全性定義.然后給出了方案的構建,并證明了方案的安全性.最后將本方案與已有方案相比較,理論與實驗分析表明該方案功能更全面性,效率更高,數據的膨脹率更低,更新計算代價更低.本方案中數據的驗證和更新不依賴于私鑰,實現了公共可驗證和公共可更新.因此本方案對外包數據庫查詢結果完整性問題的研究具有一定的理論意義和實踐價值.
e(g,g)=e(σX(α),(gαR*+1)-1)e(π*,g).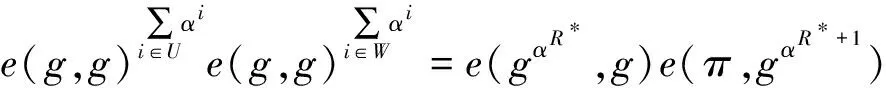
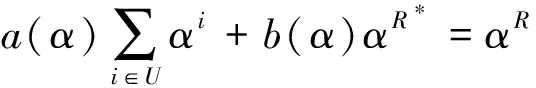
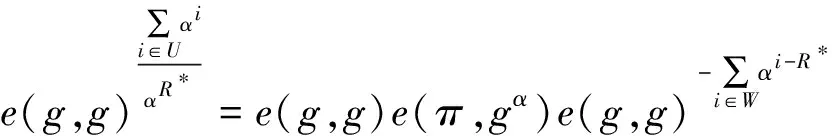
4 性能分析
4.1 方案對比
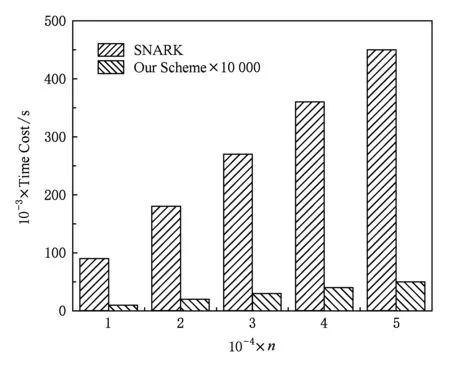
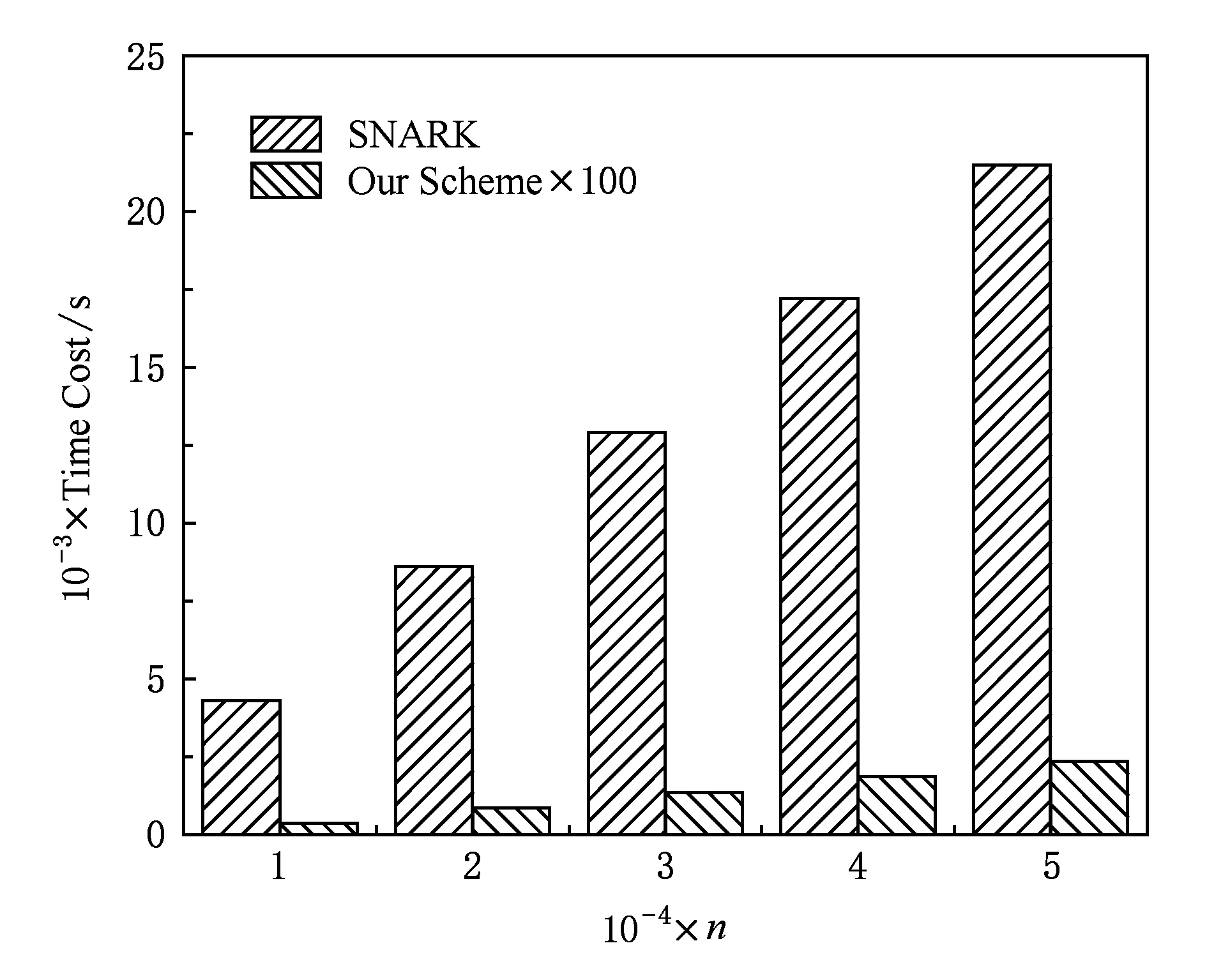
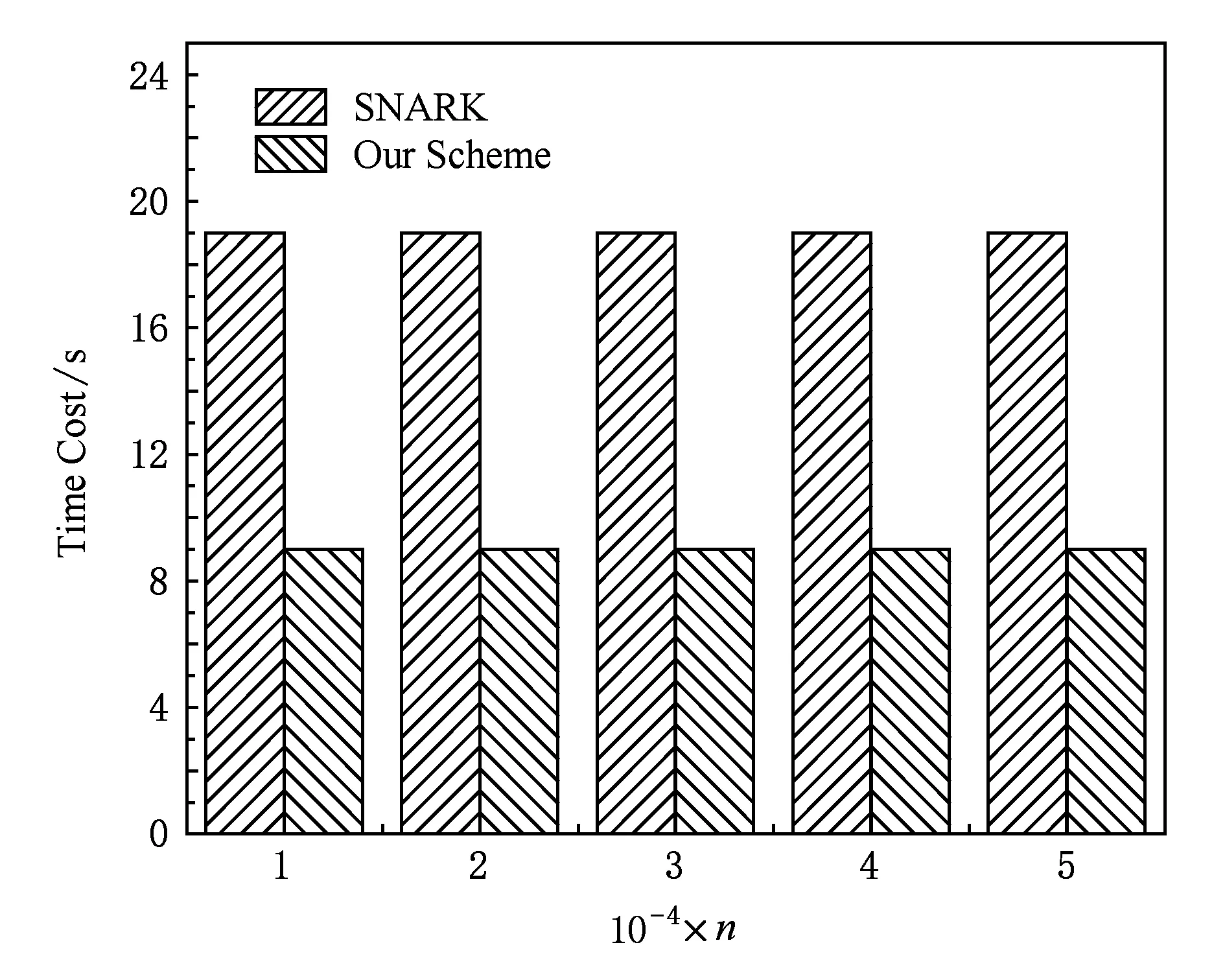
4.2 效率分析
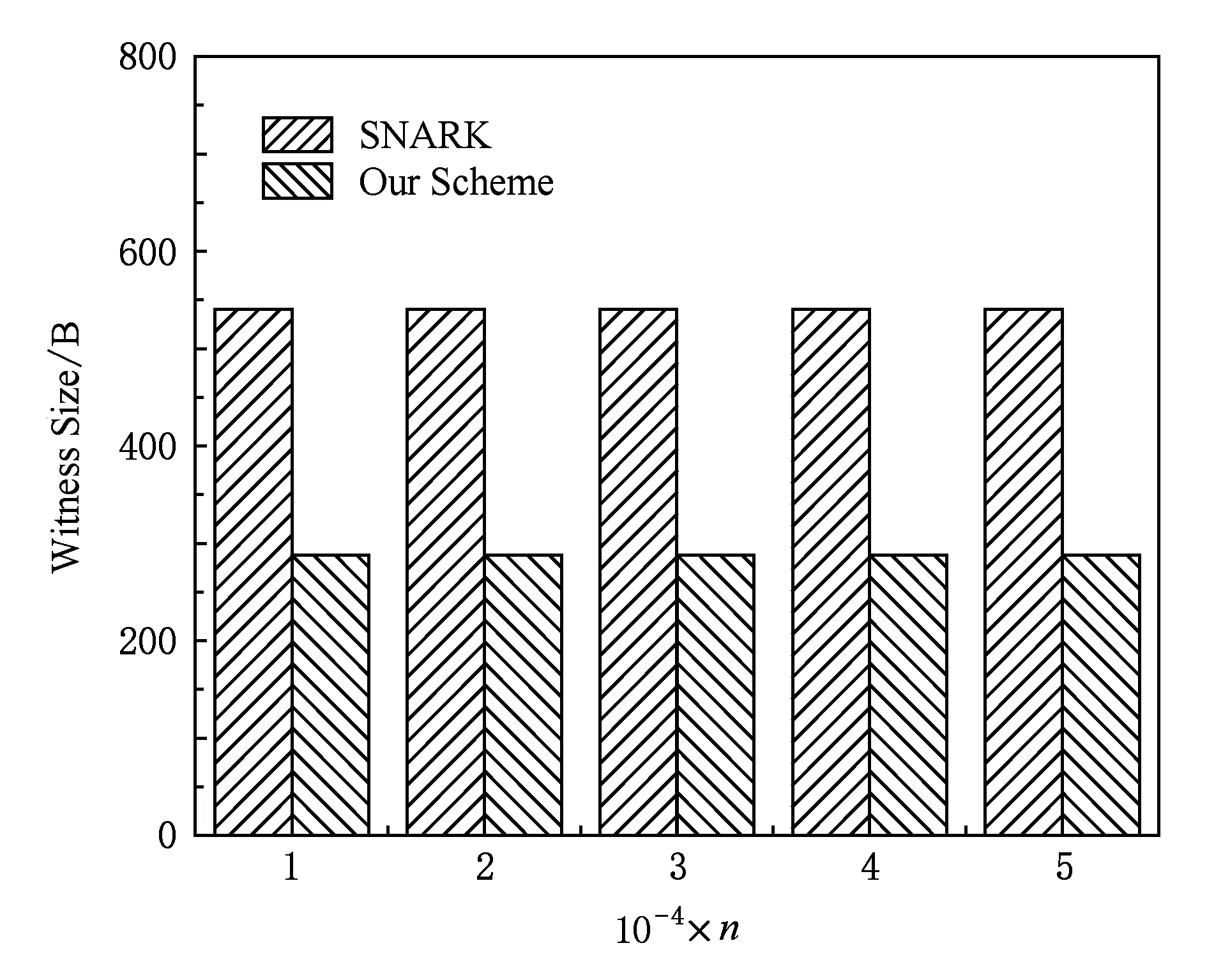
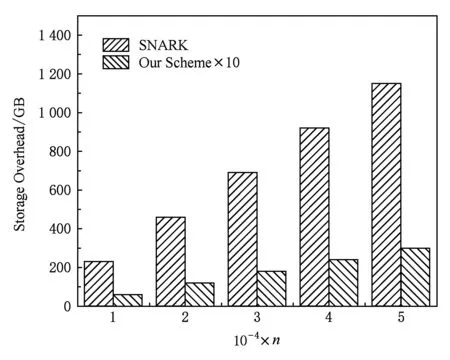
5 結 論

