一類邊界耦合波方程的穩定性
梁琦琦,馮紅銀萍
(山西大學 數學科學學院, 太原 030006)
在工程和物理學中,系統的耦合是普遍存在的。 在文獻[1]中,作者討論了ODE-熱方程的耦合系統,證明了該耦合系統是指數穩定的。文獻[2]研究了Euler-Bernoulli梁方程與熱方程在邊界耦合的系統,熱方程作為整個耦合系統的控制器,使得耦合系統的解是指數穩定的。在文獻[3-5]中,Zhang和Zuazua分別討論了熱方程和波方程在兩類不同邊界條件下的耦合,并證明了兩種情況下的耦合系統是多項式穩定的。文獻[6-7]研究了兩個波方程的主方程耦合的系統,并且證明了在不同的假設條件下系統為指數穩定或一般穩定、本文研究了一類新的邊界耦合的波方程系統,并證明了耦合系統是適定的、漸近穩定的但不是指數穩定的。
本文討論如下的耦合波方程:
(1)
其中:k,c為正常數;wx或w′表示w對x的導數,wt表示w對t的導數。令:
φ(x,t)=u(1+x,t), 0
則上述系統等價于如下的耦合系統:
(2)
因此,只需考慮耦合系統(2)的適定性和穩定性。定義系統(2)的能量函數為:
對E(t)求導,并結合(2)得到:
因此E(t)是單調遞減的。
將在如下狀態空間上考慮系統(2)的適定性和穩定性:
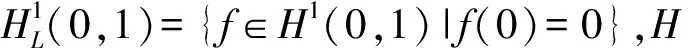
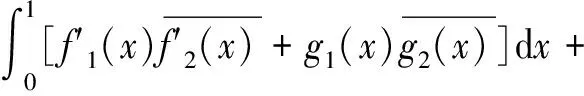
(3)
?Xi=(fi,gi,hi,mi)∈H,i=1,2
定義算子Α:D(Α)(?H)→H為:
(4)
則系統(2)可以寫成如下發展方程:
其中:X(x,t)=(w(·,t),wt(·,t),φ(·,t),φt(·,t)),X0(x)=(w0,w1,φ0,φ1)。
定理1 對任意初值(w0,w1,φ0,φ1)∈H,系統(2)有唯一的解使得(w(·,t),wt(·,t),φ(·,t),φt(·,t))∈C([0,∞);H)。此外,系統(2)的解是漸近穩定的,即:
(5)
證明算子Α由式(4)定義,則對任意的(f,g,h,m)∈D(Α),簡單計算可得:
Re〈Α(f,g,h,m),(f,g,h,m)〉=
cm(0)h(0)=-kg2(1)≤0
(6)
因此Α在H中耗散。對任意的(p,q,r,s)∈H,解方程Α(f,g,h,m)=(p,q,r,s)可得:
(7)
因此Α-1存在。根據Sobolev嵌入定理[8],Α-1在H中是緊的。由Lumer-phillips定理[9]得:Α在H上生成C0-壓縮半群。
接下來證明系統(2)是漸近穩定的。根據文獻[10]可知:只要證明算子Α在虛軸上無特征值即可。事實上,假設
Α(f,g,h,m)=iz(f,g,h,m),(f,g,h,m)∈D(Α)
其中z∈R,可以得到(f,g,h,m)滿足如下的方程組:
(8)
如果z=0,則f=g=h=m=0。現在假設z≠0,在式(8)前兩個等式兩邊分別與f,h做內積,可得:
(9)
另一方面,利用分部積分公式,有:
(10)
比較式(9)和(10)可知:
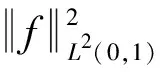
(11)
化簡可得:
(12)
比較式(12)等號兩邊的虛部可知-izk|f(1)|2=0,由于k≠0,z≠0,故f(1)=0。由式(8)得(f,h)的解:
(13)
其中系數c1、c2、c3、c4滿足如下的齊次線性方程組:
(14)
要使得方程組(13)只有零解,當且僅當方程組(14)的系數矩陣的秩為4, 即系數矩陣中有一個四級子式不為0。上述方程組的系數矩陣為:
它的四級子式分別為:
4isinz(zsinz-ccosz)
4isinz
4sinz(csinz+zcosz)
4cosz(zsinz-ccosz)
4(zsinz-ccosz)
若sinz≠0,則|A2|≠0,結論成立;若sinz=0,則cosz≠0,于是|A4|≠0,故方程組只有零解。表明Α在虛軸上沒有譜,所以eΑt是漸近穩定的。
注記1 若Α為由式(4)定義的算子,則eΑt不是指數穩定。
事實上,對任意的λ∈σ(Α),解Sturm-Liouville問題:
Α(f,g,h,m)=λ(f,g,h,m),(f,g,h,m)∈D(Α)
(15)
與定理1的第二部分證明類似,f,h式中的系數滿足如下條件:
(16)
如果上述方程組有非零解,當且僅當系數矩陣的行列式值為零,即:
(c+λ)(k+2)e2λ+(2-k)(c-λ)e-2λ-2kλ=0
這就等價于:
(17)
只考慮下面1種情況:
(18)
根據Rouche定理[11],得到如下的漸近表達:
λ=λn=nπi+O(n-1),n→∞
(19)
將式(19)代入式(18),可以得到O(n-1)所滿足的條件為:
(20)
結合式(19),可得:
(21)
這里n是整數。由此可得系統(2)不是指數穩定的。

