基于CFD的羅茨真空泵的瞬態流場計算與性能預測

黃 思，康文明，陳首挺，莫宇石

(1.華南理工大學 機械與汽車工程學院, 廣州 510640；2.廣東省肯富來泵業股份有限公司, 廣東 佛山 528000)

羅茨真空泵是一種旋轉容積式真空泵，能在較寬的壓力范圍內工作，且泵腔內無油，目前已廣泛應用于半導體、電子、石油、化工等行業的真空系統[1-2]。

羅茨真空泵運行過程中涉及熱變形、流量脈動和排氣口回流等復雜過程，難以通過理論分析進行研究。隨著CFD技術的廣泛應用，采用數值計算方法對羅茨泵內部實際流動進行模擬并分析其流動狀況成為一種有效手段。國內外學者針對羅茨泵型線、泄漏、內部流場以及進排氣流量脈動展開了深入的研究[3-17]。Hsieh等[3]利用實驗結合數值分析的方法研究了采用直齒和斜齒轉子的羅茨泵的內部流動情況，揭示了兩者的內部流動規律。Burmistrov 等[4]建立了分子流態下羅茨泵的泄漏通道流導系數的模型，充分考慮了轉子的返流對泄漏的影響。戴映紅等[13]從嚙合理論出發，研究了各種型線轉子的容積利用系數，并對羅茨真空泵內部流動情況進行了瞬態模擬。魏列江等[14]通過對羅茨泵進行數值計算，發現徑向間隙是導致泄漏的重要因素。劉正先等[15]運用動網格對羅茨泵內部排氣脈動、渦流等進行了相關研究，并修正了泄漏經驗公式。目前，關于羅茨泵的研究主要還是基于特定工況展開的，而對于不同工況下羅茨泵性能的系統全面的研究則尚不多見。本文以ZJQ-600型羅茨真空泵為研究對象，對不同壓差、轉速、轉子間隙、有無逆流冷卻、進氣溫度等條件下羅茨泵進行全面系統的研究，探究各參數對羅茨泵性能的影響，并將數值計算結果和抽速實測結果進行對比，以驗證計算模型的有效性。

1 氣體流動的控制方程

羅茨真空泵內氣體視為可壓縮理想氣體，其工作過程屬于流動與傳熱的耦合問題，滿足下列的連續性方程、動量方程、能量方程及氣體狀態方程：

(1)

(2)

(3)

(4)

其中：ui是速度矢量在i方向的分量；ρ為氣體密度；μ為動力黏度；cp為氣體比熱；λ為氣體分子導熱系數；R為氣體常數；Si為動量守恒方程的廣義源項；ST為黏性耗散相。

2 羅茨真空泵流場的計算

2.1 流體域建模與網格劃分

所研究的ZJQ-600型羅茨真空泵示意圖如圖1所示，包括吸氣腔、攜帶腔、逆流冷卻段和排氣腔，其中入口直徑D1=200 mm，出口直徑D2=150 mm，逆流冷卻口直徑D3=75 mm，中心距L=208.2 mm，轉子厚度B=420 mm，設計轉速n=1 460 r/min。逆流冷卻就是在羅茨真空泵基元容積與排氣口連通之前，從排氣口引回一部分高溫高壓氣體，經冷卻后進入圖1所示的逆流冷卻口，使基元容積內部壓力預先接近排氣壓力。

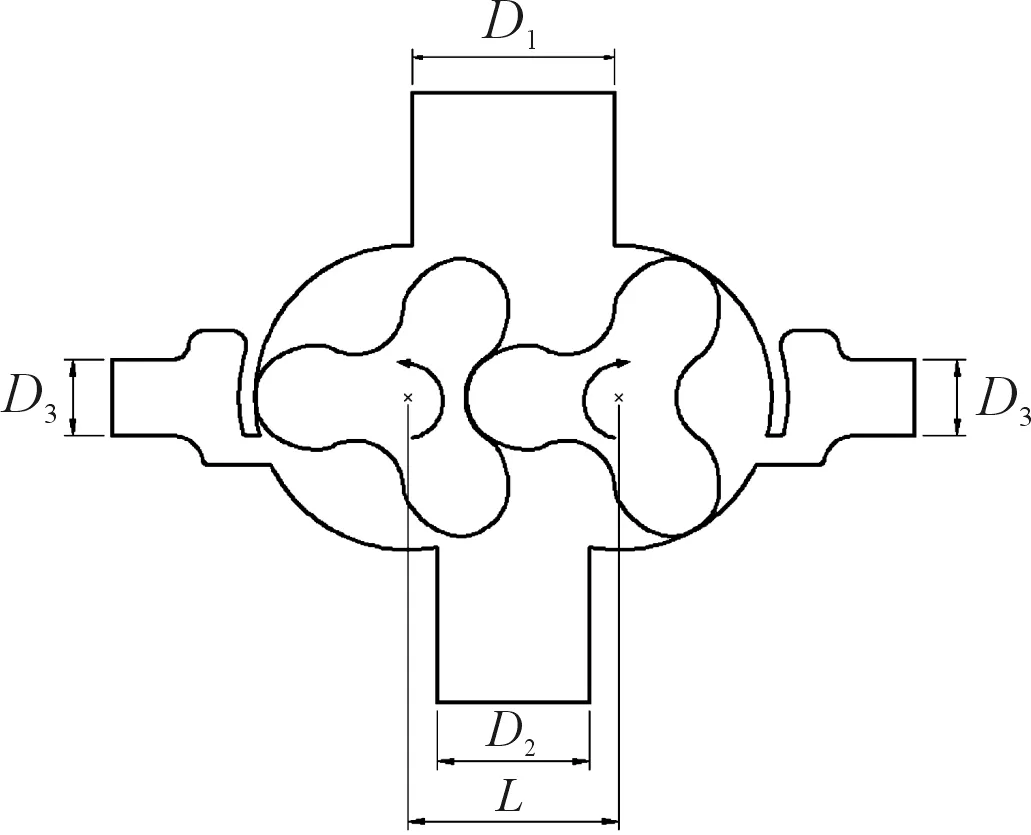
圖1 羅茨泵示意圖

由于羅茨真空泵進排氣容積呈周期性變化，計算域與網格隨時間的變形和位移十分顯著，因此在現有的CFD技術中只有動網格才能實現這種狀況下的瞬態模擬。本文采用局部網格再生成和彈性光滑模型來實現動網格以適應實際流場的需要。對建立好的流體域模型進行網格劃分，結果如圖2所示，網格總數為 473 725。

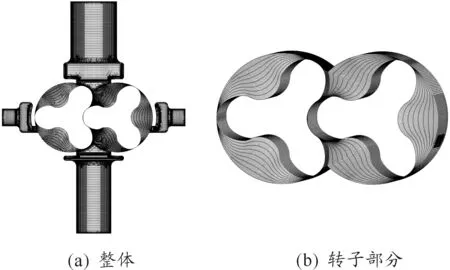
圖2 羅茨泵計算域網格劃分

2.2 操作條件設置

運用CFD動網格技術進行羅茨泵的瞬態流場計算。選擇RNGk-ε模型，該模型能夠更好地處理高應變率及流線彎曲程度較大的流動。壓力項用PRESTO格式離散。其余項用二階迎風格式離散。壓力速度耦合方程采用PISO算法求解。設置材料為理想空氣，邊界條件設置為壓力入口和壓力出口。根據羅茨泵的最大轉速，計算設置時間步長為10-5s。

2.3 計算結果驗證

設置出口壓力pd為大氣壓，分別計算入口壓力ps=101 325、60 000、45 000、30 000、25 000和20 000 Pa(絕對壓力，下同)時羅茨泵的抽速qs。圖3是不同ps下計算抽速qs在一個周期內的平均值與實測抽速的對比。由圖3可以看出：在ps比較大(大于30 000 Pa)時，計算結果與實際抽速比較接近；ps較低時(25 000 Pa)，計算結果與實際抽速偏差較大，偏差較大的原因是當進出口壓比pd/ps較大時，泵內溫度較高造成了轉子和泵殼等熱膨脹變形而產生了較多的泄漏。

2.4 內部流場分析

圖4和圖5分別是基元容積未與排氣口連通時，有、無逆流冷卻裝置羅茨泵的流速矢量和壓力分布。結合圖4、圖5可以看出：高壓冷氣持續流入逆流冷卻羅茨泵基元容積內，形成較大的旋渦，致使基元容積內壓力不斷增大，接近甚至超過排氣口壓力。圖5(b)基元容積內的2個低壓區對應于圖4(b)中的旋渦中心。無冷卻羅茨泵流動過程則相對較平穩，圖5(a)基元容積內壓力接近吸氣腔，但由于存在泄漏，基元容積內壓力在轉動過程中略有增大。

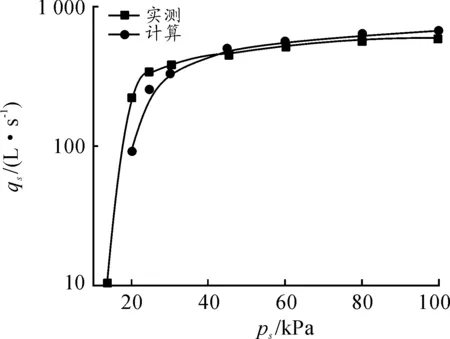
圖3 抽氣速率的實測值和模擬計算值的對比

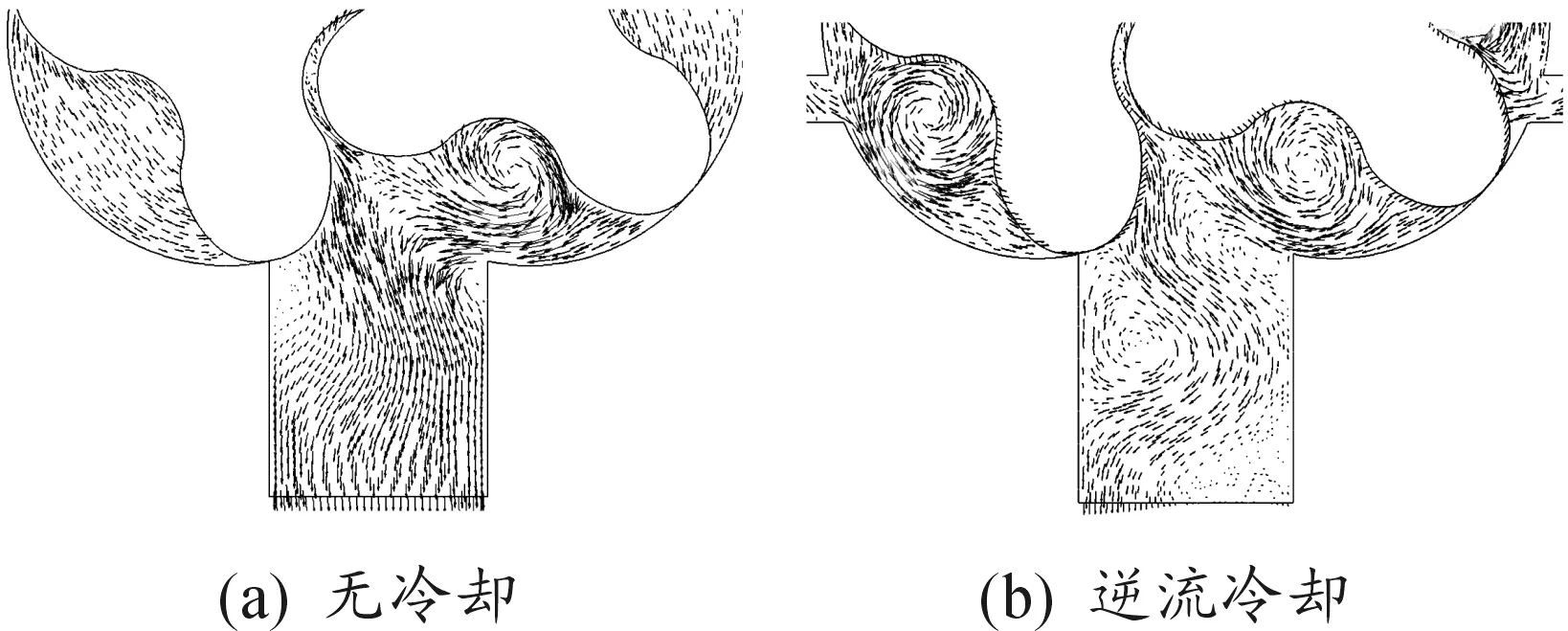
圖4 基元容積未與排氣口連通時流速矢量

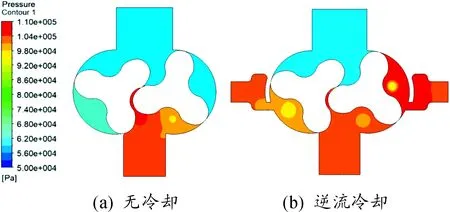
圖5 基元容積未與排氣口連通時壓力分布

圖6和圖7分別是基元容積與排氣口充分連通后有、無逆流冷卻裝置羅茨泵的流速矢量和壓力分布。結合圖6和圖7可以看出：由于逆流冷卻的預進氣使封閉的基元容積在與排氣口連通之前，內部壓力已達到或接近排氣壓力，所以此時并無明顯的回流現象，大幅度降低了排氣時的氣體回流及其帶來的氣流噪聲；無逆流冷卻羅茨泵在排氣初始時排氣腔與基元容積間存在極大的壓差，當基元容積與排氣腔連通后，排氣側的高壓氣體迅速均壓回流，圖6(a)中回流氣體與基元容積中的排出氣體相遇，在連通處形成旋渦。

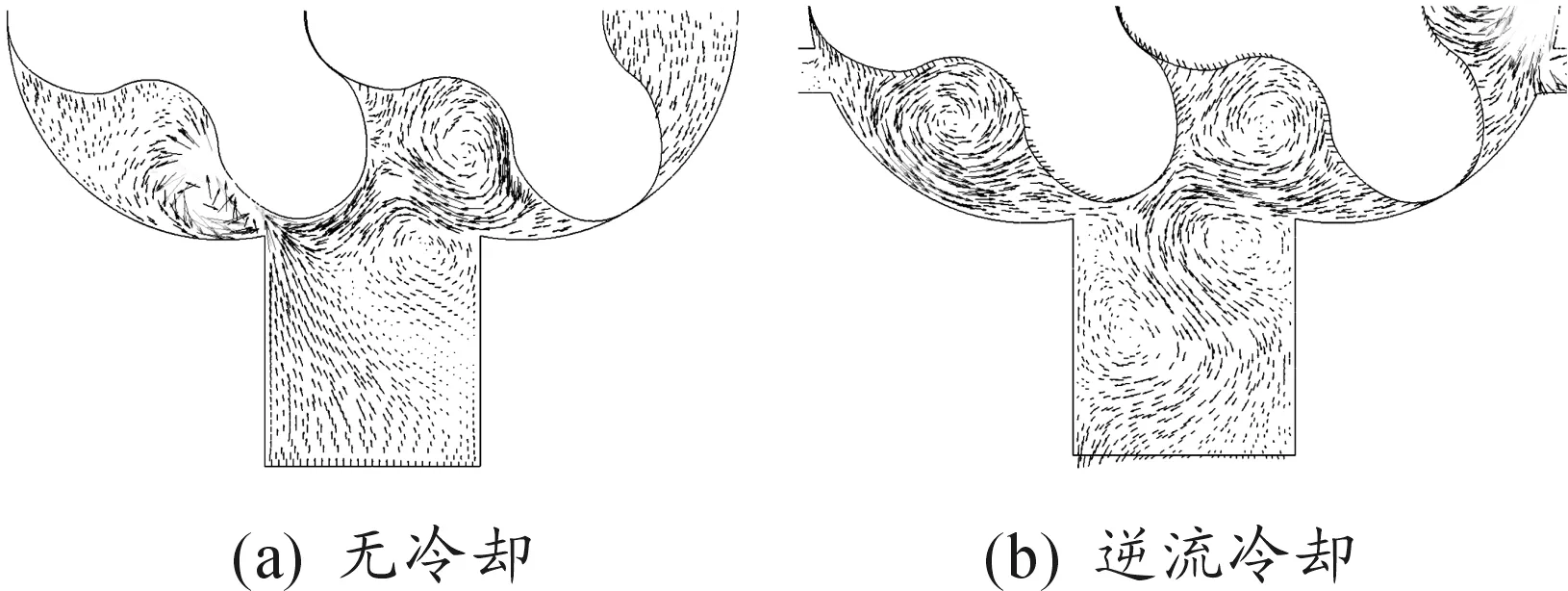
圖6 基元容積與排氣口連通后流速矢量

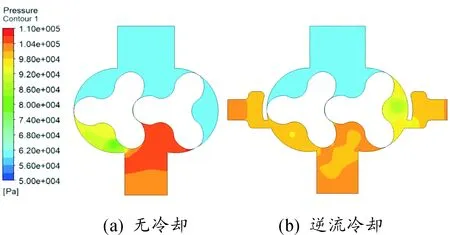
圖7 基元容積與排氣口連通后壓力分布

3 各種參數對抽速的影響

3.1 入口壓力

圖8是出口壓力為101 325 Pa時分別計算ps=101 325、60 000和45 000 Pa得到的羅茨泵穩定運行后qs隨轉動角度θ的變化，qs的平均值分別為675、550.7和496 L/s。由圖8可知：在一個轉子旋轉周期內，qs隨時間出現6次諧波變化，頻率正好是羅茨泵轉子葉片數的2倍，這是2個轉子交互作用所產生的結果。在入口壓力較高時，抽速平穩，脈動幅度小，隨著入口壓力的降低，氣體脈動強度增大。不同入口壓力下波峰的位置不同，即抽速達到最大值的轉子角度并不一致。

3.2 轉速

圖9是入口壓力6 000 Pa、出口壓力14 100 Pa和入口壓力60 000 Pa、出口壓力101 325 Pa兩種工況下的qs隨轉子轉速n(980、1 460、1 750 r/min)的變化曲線。由圖9可知：抽速和轉速大致呈線性關系，滿足流量相似定律，即幾何相似的泵在相似工況下運行時，其流量比與轉速比的一次方成正比。

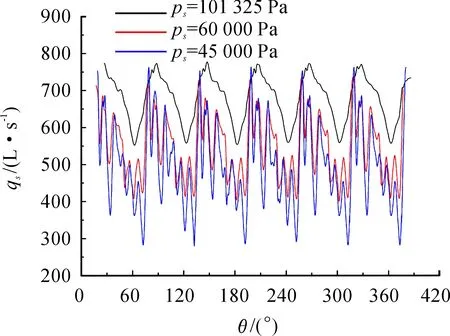
圖8 不同入口壓力下抽速隨轉子轉角的變化

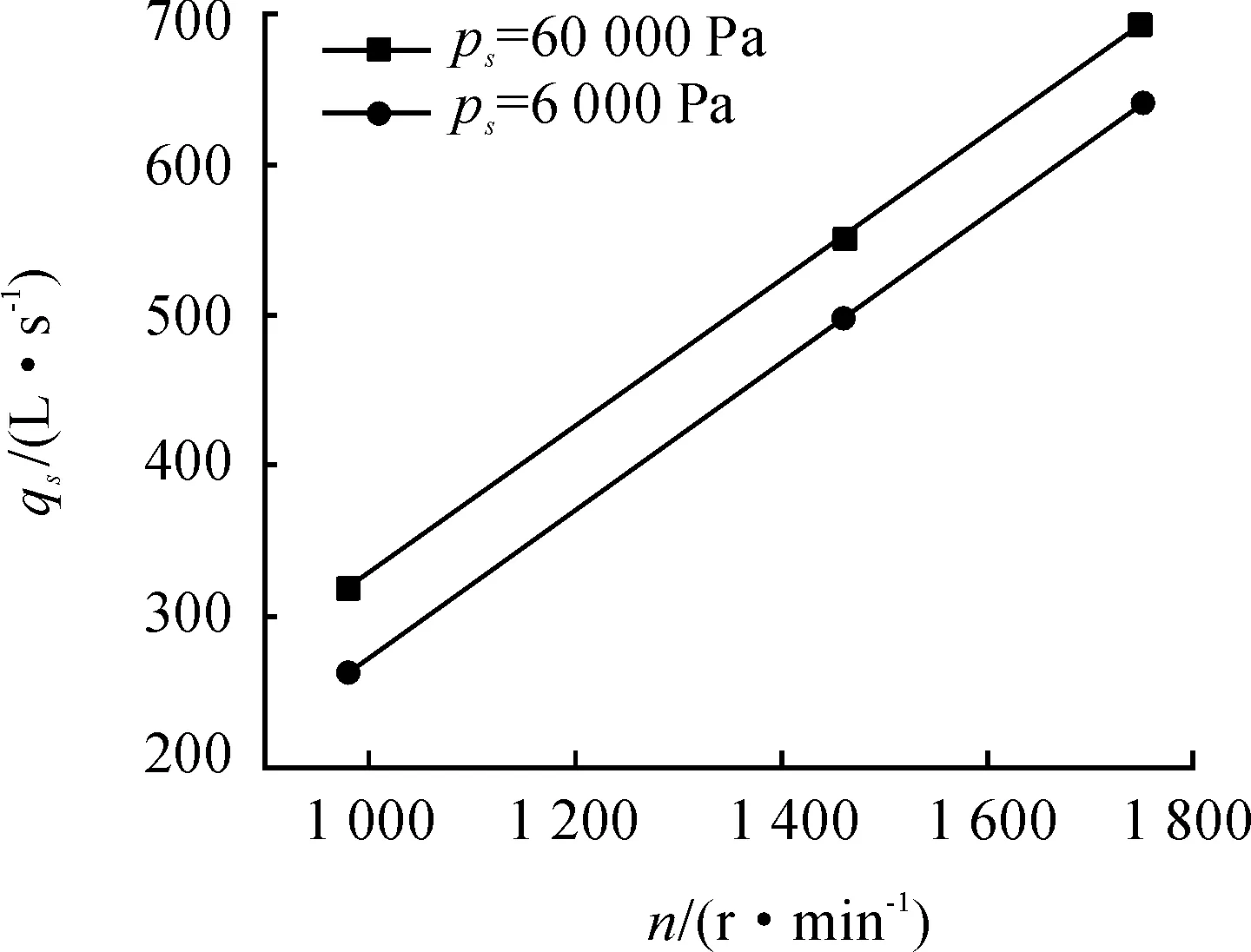
圖9 轉子轉速對抽速的影響

3.3 轉子間隙

圖10是入口壓力為 60 000 Pa，出口壓力101 325 Pa時qs隨轉子間隙δ(0.15、0.2、0.6、0.8 mm)的變化曲線。由圖10可知：抽速隨著轉子間隙的增大而逐漸減小，但減小的趨勢不斷變緩。在間隙較小時，泄漏速度較大，抽速對轉子間隙變化比較敏感。

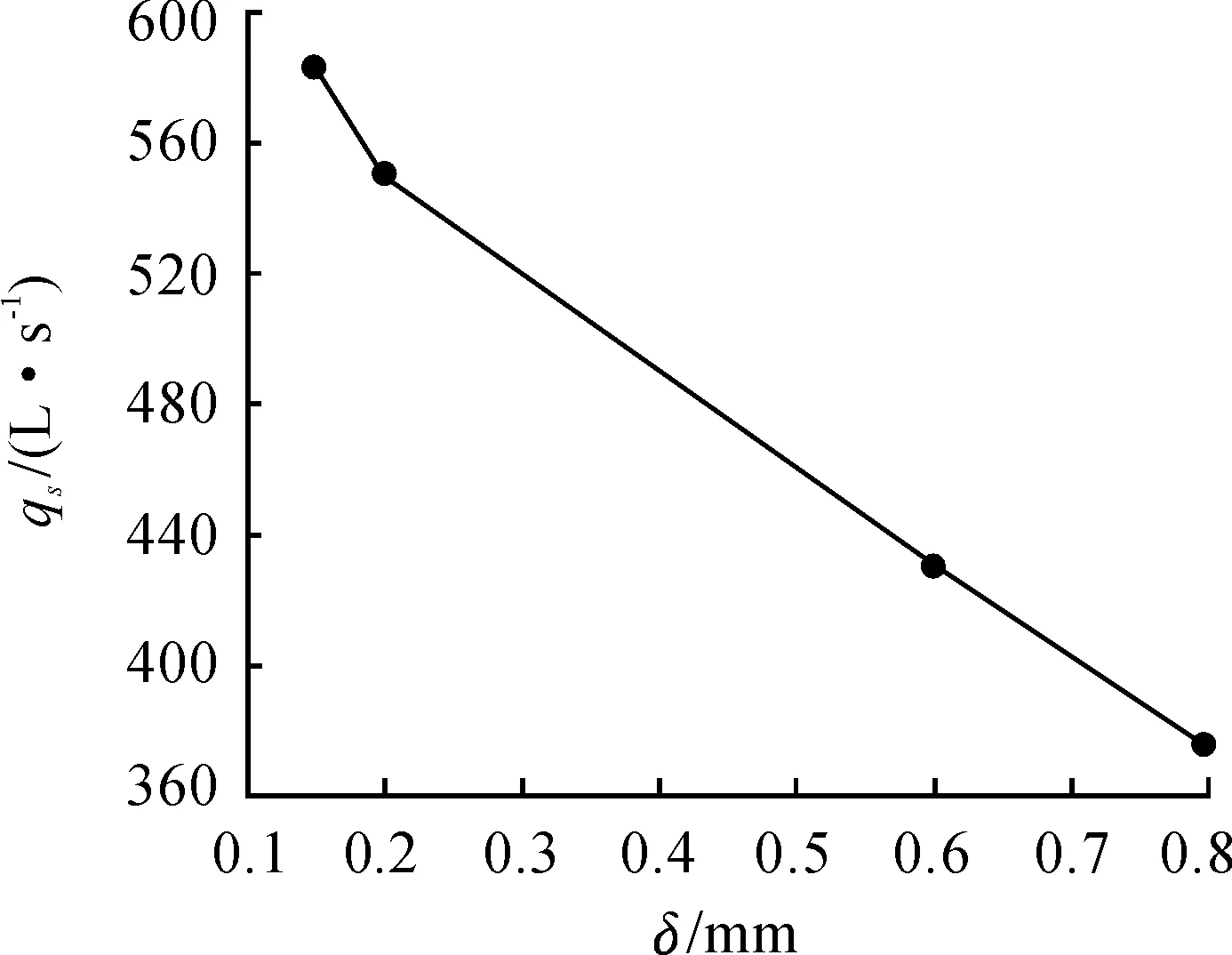
圖10 轉子間隙對抽速的影響

3.4 逆流冷卻

圖11是入口壓力為60 000 Pa時，有無逆流冷卻2種工況下羅茨泵穩定運行后qs隨轉子轉角θ的變化曲線。

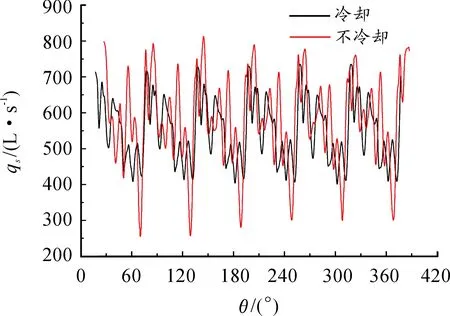
圖11 逆流冷卻對抽速的影響

由圖11可知：無逆流冷卻的抽速脈動幅度大于有逆流冷卻的羅茨真空泵，且平均抽速577.4 L/s，略大于有逆流的550.7 L/s。這是因為此時壓比不大，排氣溫度較低，當不考慮轉子及泵殼的熱膨脹變形給流體域帶來的影響時，增加逆流冷卻裝置將會使壓縮過程提前，壓縮周期延長，基元容積中氣體壓力大致接近排氣壓力，會有更多的氣體向進氣腔泄漏；同時增加逆流冷卻裝置會使基元容積以及預冷進氣通道中產生較大的旋渦，嚴重阻礙了氣體向排氣側流動。

3.5 進氣溫度

圖12是入口壓力為60 000 Pa時，進氣溫度ts分別為20 ℃和60 ℃兩種工況下羅茨泵穩定運行后qs隨轉子轉角θ的變化曲線。計算得到20 ℃和60 ℃時的平均抽速分別為550.7 L/s和547 L/s，出口排氣溫度分別為50 ℃和53 ℃。從圖12可以看出：兩者的脈動幅度和脈動頻率大致是一樣的，在同一轉子轉角時有最大抽速。在壓比較低時，進氣溫度對抽速的影響較小，抽速隨進氣溫度升高略有下降。

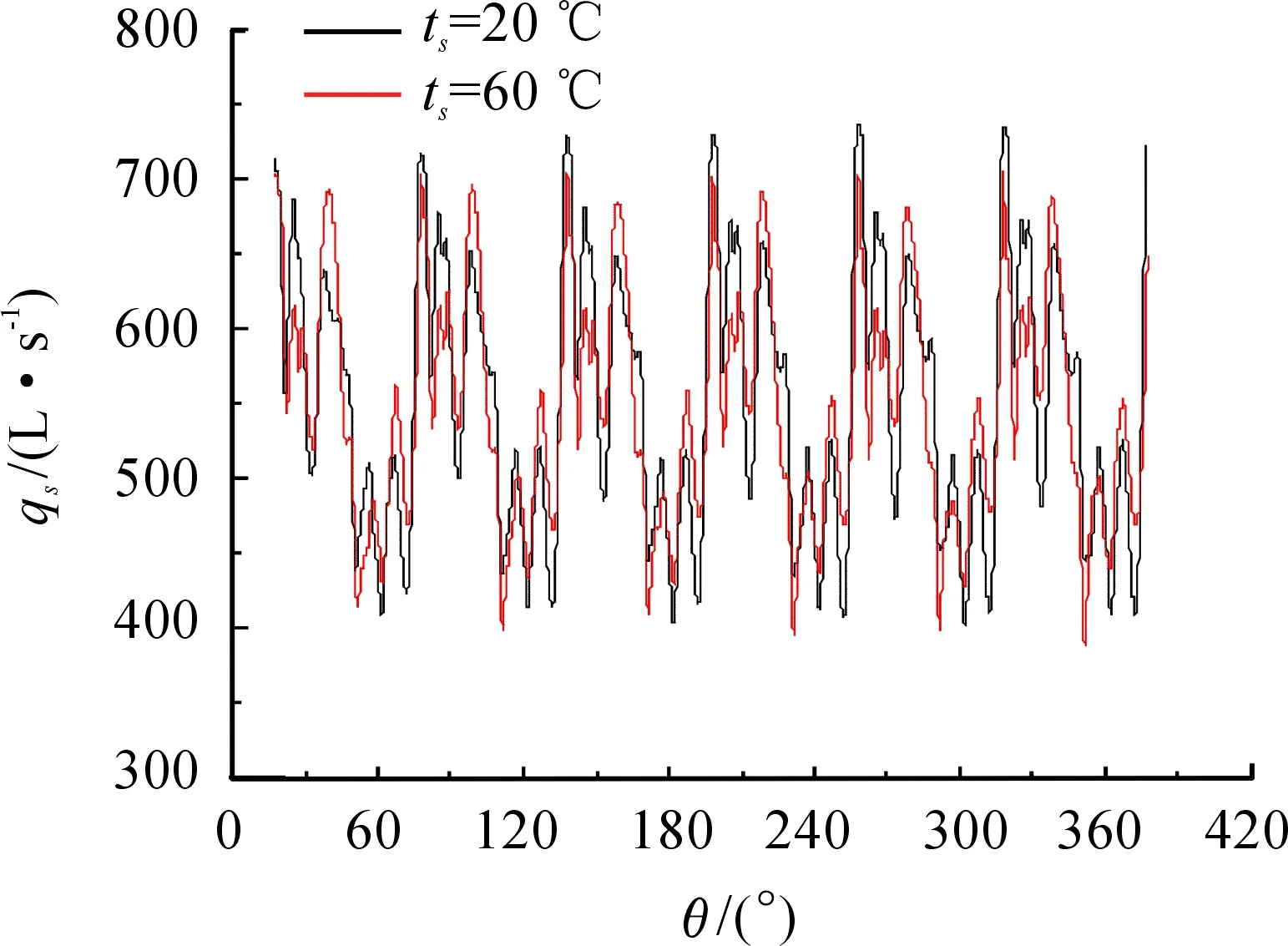
圖12 進氣溫度對抽速的影響

4 結論

本文通過對羅茨真空泵流場數值計算并與實測抽速進行了對比，得到以下結論：

1) 逆流冷卻排氣口連通之前基元容積內部壓力已達到排氣壓力，所以排氣口并無明顯的回流現象；無逆流冷卻羅茨泵在排氣初始時排氣腔與基元容積間存在極大的壓差，當基元容積與排氣腔連通后，排氣側的高壓氣體迅速均壓回流，在連通處形成旋渦。

2) 系統研究了各參數對羅茨泵性能的影響，得到羅茨真空泵的性能變化規律。出口壓力一定時，隨著入口壓力降低，抽速減小，流量脈動劇烈。抽速和轉速線性相關，近似滿足流量相似定律，抽速比與轉速比的一次方成正比。抽速隨著轉子間隙的增大而逐漸減小，但減小的趨勢不斷變緩。

3) 當壓比較小時，增加逆流冷卻會使基元容積以及預冷進氣通道中產生較大的旋渦，阻礙氣體向排氣側流動。因此，增加逆流冷卻并不能增大抽速，抽速隨進氣溫度升高略有下降。