基于貝葉斯方法優效非劣效性試驗轉換研究*
中國藥科大學生物統計與計算藥學研究中心(210009) 于 莉 蔣麗蕓 尹竹琳 言方榮
【提 要】 目的 基于Bayesian框架,討論由優效性向非劣效性試驗轉換,或由非劣效性向優效性試驗轉換時,試驗的Ⅰ類錯誤率能否控制在可接受范圍內。方法 通過不同場景下模擬得到的全局Ⅰ類錯誤率予以驗證,并對設計中的重要參數進行敏感性分析。結果 模擬結果表明,在一般條件下,全局Ⅰ類錯誤率都能很好的控制在0.1以內,而在稍加嚴格的條件下,全局Ⅰ類錯誤率可控制在0.05以內。結論 由優效性向非劣效性試驗轉換,或由非劣效性向優效性試驗轉換時,整個試驗的Ⅰ類錯誤率能得到有效的控制。
Ⅱ期臨床試驗主要用來檢驗新藥的有效性,應用安慰劑或已上市藥物作為對照藥對新藥的療效進行評估,而進行隨機臨床試驗(randomized clinical trial,RCT)是比較不同藥物療效的最佳方法。根據不同的試驗目的,可以將RCT分為優效性試驗、非劣效性試驗及等效性試驗。優效性試驗旨在驗證新藥的療效是否優于標準藥物或安慰劑;非劣效性試驗旨在驗證新藥的療效是否不比標準藥物差;等效性試驗旨在驗證新藥的療效是否與標準藥物的療效相當[1-2]。傳統的RCT設計中,根據不同的目的選擇相應的試驗類型,受試者完全入組后對所得的受試者數據進行檢驗,一旦檢驗結果不能達到預期目標,則試驗失敗,前期的投入也將付之東流。為了盡可能減少企業的損失、提高新藥申報的成功率,一個解決方法是:如果原先進行的是優效性試驗,則可以選擇下調試驗目標,再進行一次非劣效性檢驗,若二次檢驗得出該新藥滿足非劣效性,則試驗成功,可以繼續進入Ⅲ期臨床試驗[3]。而對于檢驗結果已達到預期且有望達到更高目標時,同樣可以上調試驗目標,對應的過程即由非劣效性試驗“升級”為優效性試驗。
歐盟藥品局(European Medicines Agency,EMA)曾出臺指導原則[4]專門探討了這種上調或下調試驗目標的方法:即當優效性檢驗的結果不顯著時,若能接受非劣效性的結果且存在預設的非劣效邊界,則可以下調試驗目標,進行非劣效性檢驗;當非劣效性檢驗的結果有可能超出預期達到優效性時,則可以進行一次優效性檢驗加以驗證。然而,一個核心的問題是如何在進行兩次檢驗時控制Ⅰ類錯誤。通常,對于單個的假設檢驗,需要將Ⅰ類錯誤率控制在0.1或0.05以內;而上述優效性試驗轉換為非劣效性試驗或非劣效性試驗轉換為優效性試驗的過程中,由于改變了試驗目的,需要進行兩次假設檢驗,若每次檢驗的Ⅰ類錯誤率都控制在0.05以內,那么進行兩次檢驗自然就遇到全局Ⅰ類錯誤率是否會膨脹的問題,然而,EMA的指導原則中并未做出詳細說明。綜上,本文基于貝葉斯框架對優效非劣效試驗相互轉換問題進行了研究,并通過多種場景下的模擬,探討了在這種轉換試驗目標的情況下其Ⅰ類錯誤率的控制問題。
原理及方法
1.優效性試驗及非劣效性試驗的假設檢驗原理
優效性試驗是為了證明新藥的療效優于已存在的藥或安慰劑,其原假設(H01)為新藥的反應率(pT)不高于標準藥的反應率(pC),備擇假設(H11)為新藥的反應率(pT)高于標準藥的反應率(pC),即
H01:pT≤pCH11:pT>pC+δ
其中δ為優效邊界。
非劣效性試驗[5]是為了證明新藥的療效不比已存在的藥差,其原假設(H02)為新藥的反應率(pT)低于標準藥的反應率(pC)且超出了臨床可接受范圍,備擇假設(H12)則為新藥的反應率(pT)不比標準藥的反應率(pC)差,即
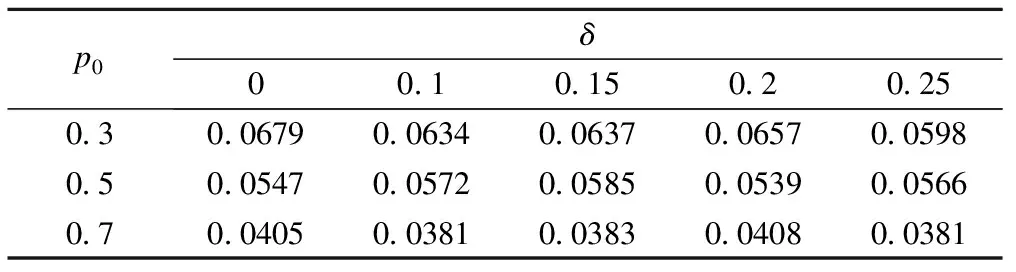
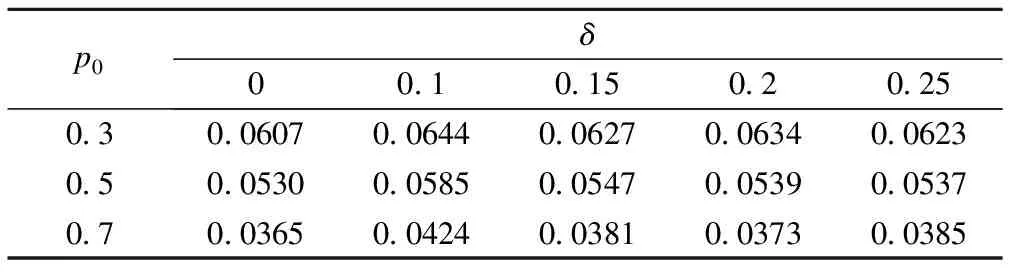
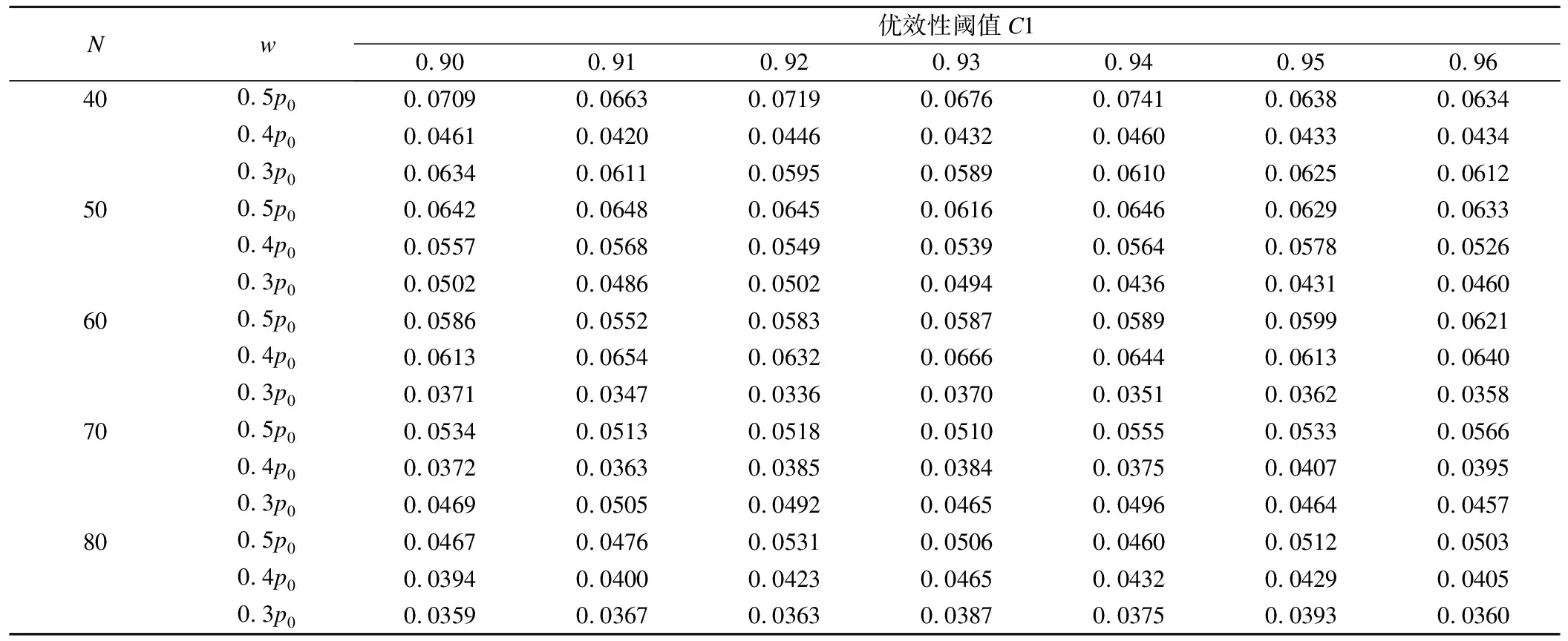
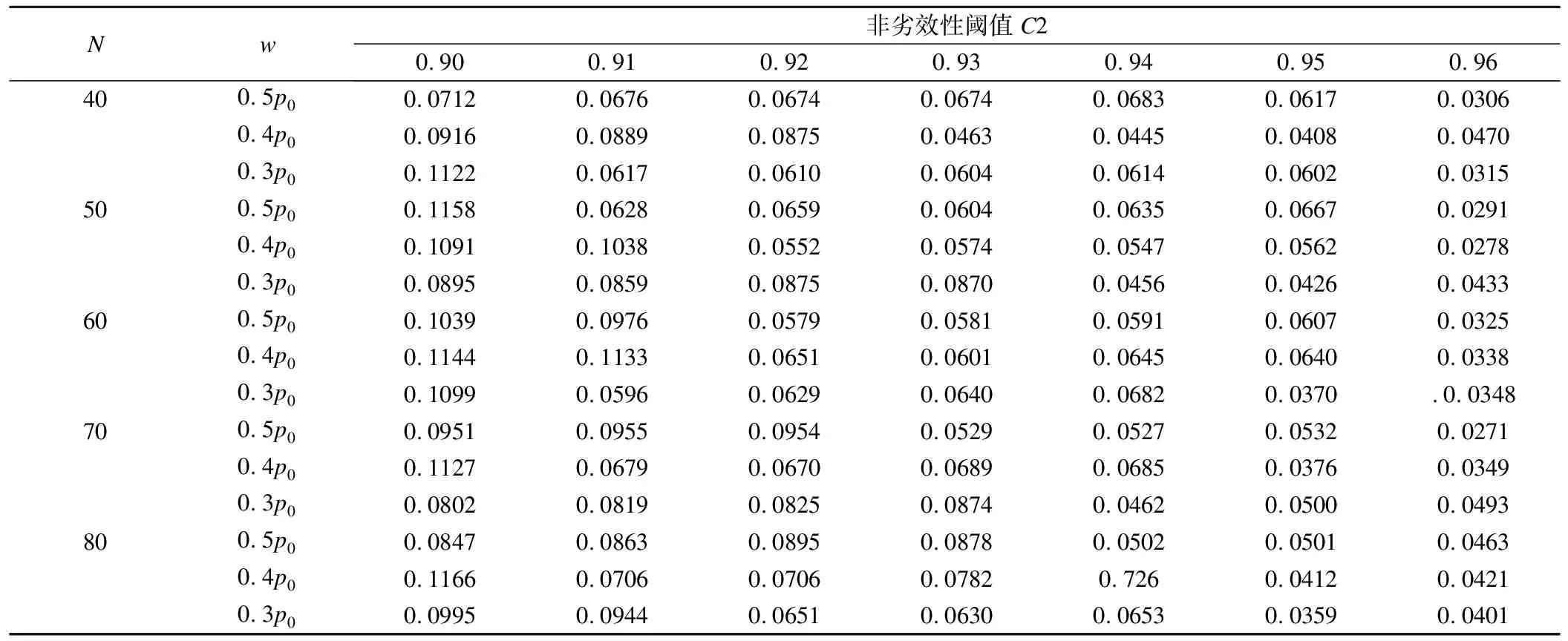
H02:pT 其中w為非劣效邊界[6-7]。 本文采用雙臂試驗,且選用陽性對照。假定實驗組和對照組分別入組N個受試者,各組有療效反應的人數分別為y1,y2,假定新藥和標準對照藥的有效反應率服從先驗分布beta(a,b),由共軛性可知,后驗分布分別為pT|Dn~beta(a+y1,b+m-y1),pC|Dn~beta(a+y2,b+m-y2)。 2.優效性試驗轉為非劣效性試驗 優效性轉非劣效性試驗流程如圖1a所示: (1)首先進行優效性檢驗。入組預定數目的受試者,根據所得的受試者數據判斷新藥比標準藥物有效的后驗概率值Pr(pT>pC+δ|Dn)是否滿足Pr(pT>pC+δ|Dn)≥C1(C1為優效性閾值,一般在(0.9,1)內取值),若滿足,則拒絕H01,認為新藥的療效優于標準藥;否則,接受H01,說明新藥的療效不理想,則進一步接受條件更為寬松的檢驗,即非劣效性檢驗。 (2)進行非劣效性檢驗。根據已獲得的受試者信息判斷新藥不比標準藥差的后驗概率值Pr(pT≥pC-w|Dn)是否滿足Pr(pT≥pC-w|Dn)≥C2(C2為非劣效性閾值,一般在(0.9,1)內取值),若滿足,則拒絕H02,認為新藥的療效不劣于標準對照藥;否則,接受H02,認為新藥比標準藥差,且超出了臨床可接受范圍。 圖1 流程圖,a為優效性轉非劣效性試驗流程,b為非劣效性轉優效性試驗流程 3.非劣效性試驗轉為優效性試驗 非劣效性轉優效性試驗流程與上述相反,如圖1b所示: (1)首先進行非劣效性檢驗。入組預定數目的受試者,根據所得的受試者數據判斷新藥療效不比標準藥差的后驗概率值Pr(pT≥pC-w|Dn)是否滿足Pr(pT≥pC-w|Dn)≥C2(C2為非劣效性閾值,一般在(0.9,1)內取值),若不滿足,則接受H02,認為新藥與標準藥相比療效太差,不能接受;否則,拒絕H02,說明新藥療效可觀,則接受進一步的條件更為嚴格的檢驗,即優效性檢驗。 (2)進行優效性檢驗。根據已獲得的受試者信息判斷新藥比標準藥物有效的后驗概率值Pr(pT>pC+δ|Dn)是否滿足Pr(pT≥pC-w|Dn)≥C1(C1為優效性閾值,一般在(0.9,1)內取值),若滿足,則拒絕H01,認為新藥的療效與標準藥相比更優;否則,接受H01,認為新藥的療效并不優于標準藥,但也不過差于標準藥,即為非劣效的。 4.全局Ⅰ類錯誤 第Ⅰ類錯誤,也稱為“棄真”錯誤,是指在統計檢驗時,在原假設H0為真的情況下,作出了拒絕原假設,即“棄真”的一種錯誤推斷,Ⅰ類錯誤可記為Pr(H1|H0)。在本文中,以上述非劣效性試驗轉為優效性試驗為例,其步驟為先進行非劣效性檢驗,若拒絕原假設H02則進行優效性檢驗,當試驗最終得到非劣效結果(接受H01)為“真”時,卻做出優效或劣效的推斷(拒絕H01),則犯了Ⅰ類錯誤。由于優效性檢驗是在H02不成立的條件下進行的,所以該Ⅰ類錯誤(拒絕H01)其實是綜合考慮了本設計中的兩個假設檢驗,故稱為全局Ⅰ類錯誤。 根據封閉檢驗原理[8],即當需要檢驗多個假設且整體Ⅰ類錯誤率為α時,如果在局部水平α上拒絕了涉及H0i的所有可能的交叉假設,則可以在α水平上拒絕H0i。同樣地,對于上例中存在兩個假設檢驗的情況,若在α水平上拒絕了H01∩H02,則可以在α水平上拒絕H01。由對兩個檢驗的原假設的定義可知H01∩H02=H02,因此,換句話說,在非劣效性試驗轉為優效性試驗的情況下,若非劣效性檢驗的Ⅰ類錯誤率(拒絕H02)能控制在α水平上,則全局Ⅰ類錯誤率理論上可以控制在α水平上。同理,在優效性試驗轉為非劣效性試驗的情況下,若在α水平上拒絕了H01∩H02,則可以在α水平上拒絕H02,由于H01∩H02=H02,所以同上,全局Ⅰ類錯誤率仍然可控制在水平α上。 綜上可知,當優效非劣效性試驗相互轉換時,其全局Ⅰ類錯誤率能夠得到有效的控制,且由非劣效性檢驗的Ⅰ類錯誤率決定。 1.模擬試驗設置及結果 設計中涉及到的參數:(p0,δ,w,C1,C2,N),p0為標準藥的初始有效反應率,δ為優效邊界,w為非劣效邊界,C1為優效性閾值,C2為非劣效性閾值,N為最大樣本量。假定一組取值:p0=(0.3,0.5,0.7),δ=(0,0.1,0.15,0.2,0.25),w=0.5*p0,C1=C2=0.95,N=50,并采用無信息先驗beta(0.6,1.4)作為pT、pC的先驗分布進行模擬。 表1、2分別為優效性試驗轉為非劣效性試驗以及非劣效性試驗轉為優效性試驗的10000次模擬結果,從數據可以直觀地看出,在p0與δ的不同取值下Ⅰ類錯誤率都能控制在0.1以內。 通過以上模擬,進一步驗證了存在多個假設檢驗的情況下,全局Ⅰ類錯誤率能夠控制在合理的范圍內,即不會出現全局Ⅰ類錯誤率膨脹的情況。 表1 優效性試驗轉為非劣效性試驗的10000次模擬結果 表2 非劣效性試驗轉為優效性試驗的10000次模擬結果 2.敏感性分析 由表1、2可以看出,標準藥的初始有效反應率p0對試驗的Ⅰ類錯誤率有較大影響,且隨著p0的增大呈下降趨勢;而優效邊界δ的變化對試驗的Ⅰ類錯誤率幾乎無影響。 進一步考慮樣本量N、非劣效邊界w及閾值C1、C2的變動對全局Ⅰ類錯誤率的影響。其余變量值固定為:p0=0.3,δ=0.1。以優效性試驗轉為非劣效性試驗為例,模擬結果見表3、4(非劣效性試驗轉為優效性試驗結果類似),其中第一行為閾值的幾種取值情況,第一列表示樣本量,對于每個樣本量值,有3種非劣效邊界的取值。 由表3、4可以看出,全局Ⅰ類錯誤率基本可以控制在0.1以內。不同樣本量N之間的全局Ⅰ類錯誤率有所差異,但總體來看差異并不明顯;不同的非劣效邊界w對試驗的Ⅰ類錯誤率有一定的影響;優效性閾值C1的變動對全局Ⅰ類錯誤率幾乎無影響,而對于不同的非劣效性閾值C2,試驗的Ⅰ類錯誤率波動很大。當C2=0.9時,Ⅰ類錯誤率較大在0.1左右,當C2=0.96時,Ⅰ類錯誤率均小于0.05,總的來說,試驗的Ⅰ類錯誤率隨著C2的增加呈下降趨勢。 表3 優效轉非劣效試驗中樣本量N、非劣效邊界w及優效性閾值的變動對全局Ⅰ類錯誤率的影響 *:此時C2固定為0.95。 表4 優效轉非劣效試驗中樣本量N、非劣效邊界w及非劣效性閾值的變動對全局Ⅰ類錯誤率的影響 *:此時C1固定為0.95。 模擬研究結果表明,無論是優效性試驗轉換為非劣效性試驗還是非劣效性試驗轉換為優效性試驗,一般條件下,其Ⅰ類錯誤率都能控制在0.1以內,而在稍加嚴格的條件下,如增大非劣效性閾值,則全局Ⅰ類錯誤率可控制在0.05以內。 通過敏感性分析可知,非劣效性閾值對試驗的Ⅰ類錯誤率的影響很大,甚至會影響到定性判斷,這是因為非劣效性閾值的大小直接影響到了非劣效性檢驗的Ⅰ類錯誤率從而導致全局Ⅰ類錯誤率的較大變化。由以上數據可直觀地看出,當非劣效性閾值的取值大于0.91時是比較安全的,即能確保Ⅰ類錯誤率小于0.1。推薦非劣效性閾值取為0.95,此時的Ⅰ類錯誤率幾乎在0.05左右;若考慮進一步削減試驗的Ⅰ類錯誤率,則可以選擇稍大一點的非劣效性閾值,如0.96,此時的全局Ⅰ類錯誤率均控制在0.05以內。而不同的標準藥初始有效反應率p0對試驗的Ⅰ類錯誤率也有較大影響,p0越大,試驗的Ⅰ類錯誤率則越小。p0的取值一般根據標準藥的歷史試驗給出。 對于其他參數的取值,其中優效性閾值一般取為0.95,由于該閾值對全局Ⅰ類錯誤率的影響甚微,因此也可以在其附近取值。而非劣效邊界值一般情況下可以取0.5*p0(p0為標準對照藥的初始有效反應率),但最優的非劣效邊界值并非是固定的,需視不同藥物的情況而定。 本文基于貝葉斯框架就優效性試驗與非劣效性試驗轉換時Ⅰ類錯誤率的控制問題進行了模擬研究分析,驗證了其全局Ⅰ類錯誤率能得到有效的控制,證明了優效性試驗與非劣效性試驗相互轉換的可行性,在實際臨床中可加以應用。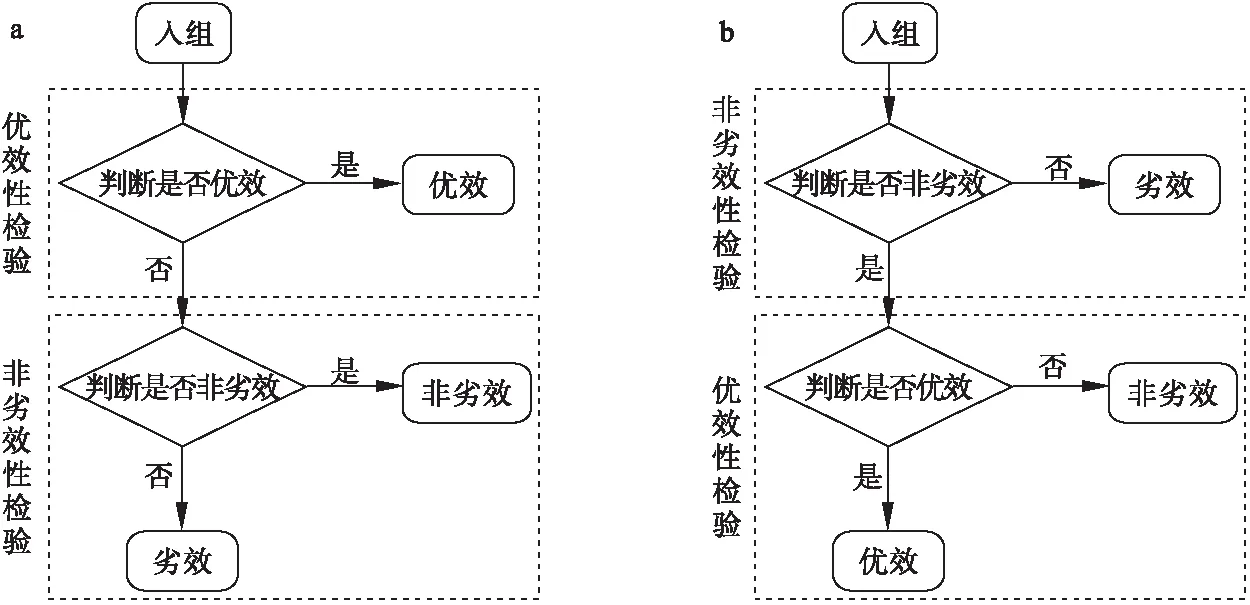
模 擬
討 論

