大氣PM2.5中多環芳烴濃度缺失值填補方法的研究
王燚烊 王瑞福 武建輝△
【提 要】 目的 研究大氣PM2.5中多環芳烴(PAHs)濃度缺失值的填補方法。方法 采用Pearson相關分析16種∑PAHs濃度與氣象因素及大氣污染物的相關關系;采用Box-Cox變換、多元線性逐步回歸法和曲線擬合法擬合回歸方程,將缺失的16種∑PAHs濃度作為因變量,相關變量作為自變量,以預測值作為PAHs濃度填補值。結果 16種∑PAHs濃度與平均溫度、風速和日照小時數呈負相關,與平均相對濕度和平均氣壓呈正相關,與PM2.5、PM10、SO2、NO2濃度呈正相關,與O3呈負相關。氣象因素中平均溫度對16種∑PAHs濃度影響最大,大氣污染物中PM2.5對16種∑PAHs濃度影響最大,回歸方程預測的2017年16種∑PAHs濃度與實測的比較,結果顯示均無差別。結論 對數據Box-Cox變換后采用多元線性逐步回歸法建立16種∑PAHs濃度與平均溫度和平均風速的回歸方程,回歸模型擬合效果較好,可用來填補缺失的PAHs濃度。
隨著空氣污染的加劇,大氣PM2.5中的多環芳烴(PAHs)由于具有隨顆粒物遠距離遷移的特征,而受到了國內外學者的關注,很多地區都開展了大氣中PAHs濃度的監測[1],國內大氣PM2.5中PAHs對人群健康影響的研究受到廣泛關注[2]。而在PAHs濃度的收集過程中缺失數據是不可避免的,如果忽略缺失數據,直接把獲得觀測值的先后順序當作時間順序來建模,勢必會得到錯誤的擬合模型[3]。
填補法是對各種填補措施的總結概括,常見的填補法有替代法和建模估計法[3]。唐山市的路北監測點由于時間和條件的限制,樣品的采集不是逐日開展的,為填補PAHs濃度缺失值,采用Box-Cox變換、多元線性逐步回歸法和曲線擬合法擬合方程填補缺失的PAHs濃度。
材料與方法
1.資料來源
(1)PAHs濃度 PAHs濃度數據來源于2015年1月-2017年12月唐山市路北監測點,在固定采樣日(每月10~16日)和霾日(AQI>200)進行PM2.5采樣,利用高效液相色譜法成分分析得到PAHs的濃度。
(2)大氣污染物濃度 同期的大氣污染物濃度資料來源于唐山市6個國控大氣環境監測站點,由唐山市環境保護局監測。
(3)氣象資料 同期氣象數據來源于唐山市氣象局,主要包括平均氣壓(hpa)、平均溫度(℃)、日平均風速(m/s)、平均相對濕度(%)和日照小時數(h)。
2.統計學方法
用SPSS 19.0和R 3.4.4軟件進行統計分析;Pearson相關分析16種PAHs濃度與氣象因素和大氣污染物的相關性;利用Box-Cox變換、多元線性逐步回歸法和曲線擬合法擬合回歸方程,將缺失變量PAHs濃度作為因變量,相關變量為自變量,以預測值作為PAHs濃度填補值,對未監測的PAHs濃度進行填補。
結 果
1.相關性分析
表1為2015-2016年PAHs濃度與氣象因素和大氣污染物之間的Pearson相關系數。結果顯示,PAHs濃度與平均溫度、風速之間呈負相關,與平均相對濕度和平均氣壓之間呈正相關;與PM2.5、PM10、SO2、NO2濃度呈正相關,與O3呈負相關。
2.路北監測點16種∑PAHs濃度與氣象因素的多元線性逐步回歸方程
(1)16種∑PAHs濃度與氣象因素的多元線性逐步回歸方程
多元線性逐步回歸分析2015年1月-2016年12月氣象因素與16種∑PAHs濃度的關系,運用逐步法,α入=0.10,α出=0.15,最后篩選進入方程的是平均溫度和平均風速。直線方程為:
Y1=307.999-7.718X1-50.463X2
式中Y1表示16種PAHs總濃度,ng/m3;X1表示平均溫度,℃;X2表示風速,m/s。
結果顯示,擬合的回歸方程有統計學意義(P<0.05)。X1的標準化回歸系數為-0.577,X2的標準化回歸系數為-0.305,說明平均溫度對16種多環芳烴總濃度影響最大。
(2)Box-Cox變換后16種∑PAHs濃度與氣象因素的多元線性逐步回歸方程

表1 PAHs與大氣污染物和氣象因素之間的Pearson相關系數
注:a為P<0.01;b為P<0.05;c為P>0.05
對因變量Y進行Box-Cox變換,不同取值λ(-2≤λ≤2),用R中的boxcox函數采用最大似然估計法進行估計[4],計算其似然函數的最大值ln(Lmax(λ)),圖1為似然函數的最大值ln(Lmax(λ))隨λ變化的曲線,結果顯示:λ=0時,ln(Lmax(λ))的值最大。

圖1 似然函數的最大值ln(Lmax(λ))隨λ變化的曲線
根據似然原理,λ=0時為對數變換,對因變量Y經Box-Cox變換后的數據再次進行多元線性逐步回歸分析[5],回歸方程為:

(3) Box-Cox變換后建立的16種∑PAHs濃度與氣象因素方程的回歸診斷
圖2為Box-Cox變換后建立的16種∑PAHs濃度與氣象因素方程的回歸診斷結果,結果顯示,變換后建立的回歸方程滿足正態性的假設,滿足方差齊性的條件。
3.路北監測點16種∑PAHs濃度與大氣污染物的多元線性逐步回歸方程
(1) 16種∑PAHs濃度與大氣污染物的多元線性逐步回歸方程
多元線性逐步回歸分析2015年1月-2016年12月16種∑PAHs濃度與大氣污染物的關系,α入=0.10,α出=0.15,最后篩選進入方程的是PM2.5、PM10、O3和SO2。直線方程為:
Y2=153.151-0.152X3+0.42X4-0.269X5+0.141X6

圖2 Box-Cox變換后16種∑PAHs濃度與氣象因素方程的回歸診斷
式中Y2表示路北監測點16種多環芳烴總濃度,ng/m3;X3表示O3,μg/m3;X4表示PM2.5,μg/m3;X5表示PM10,μg/m3;X6表示SO2,μg/m3。
結果顯示,擬合的回歸方程有統計學意義(P<0.05)。X3的標準化回歸系數為-0.368,X4的標準化回歸系數為1.267,X5的標準化回歸系數為-1.084,X6的標準化回歸系數為0.171,說明PM2.5對16種多環芳烴總濃度影響最大。
(2) Box-Cox變換后16種∑PAHs濃度與大氣污染物濃度的多元線性逐步回歸方程
對因變量Y進行Box-Cox變換,圖3為似然函數的最大值ln(Lmax(λ))隨λ變化的曲線,結果顯示:λ=0時,ln(Lmax(λ))的值最大。
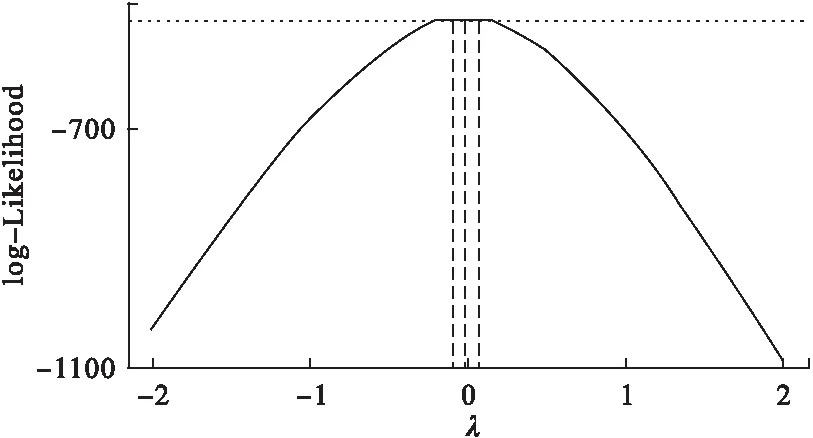
圖3 似然函數的最大值ln(Lmax(λ))隨λ變化的曲線
對因變量Y經Box-Cox變換后的數據再次進行多元線性逐步回歸分析,回歸方程為:
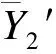
(3) Box-Cox變換后建立的16種∑PAHs濃度與大氣污染物濃度方程的回歸診斷
圖4為Box-Cox變換后建立的16種∑PAHs濃度與大氣污染物回歸方程的回歸診斷結果,結果顯示,Box-Cox變換后建立的多元線性回歸方程滿足正態性的假設,方差齊。
4.曲線擬合法建立路北監測點16種∑PAHs 濃度與平均溫度的方程
(1) 平均溫度與路北監測點16種∑PAHs的回歸方程
直線回歸分析2015年1月-2016年12月路北監測點16種∑PAHs濃度與平均溫度的關系,直線方程為:
Y3=201.444-8.217X7

圖4 Box-Cox變換后16種∑PAHs濃度與大氣污染物濃度方程的回歸診斷
式中Y3表示路北監測點16種多環芳烴總濃度,ng/m3;X7表示平均溫度,℃。
(2) Box-Cox變換后16種PAHs濃度與平均溫度的回歸方程
對因變量Y進行Box-Cox變換,圖5為似然函數的最大值ln(Lmax(λ))隨λ變化的曲線,結果顯示:λ=0時,ln(Lmax(λ))的值最大。
根據似然原理,λ=0時為對數變換,對因變量Y經Box-Cox變換后的數據再次進行直線回歸分析[5]。回歸方程為:
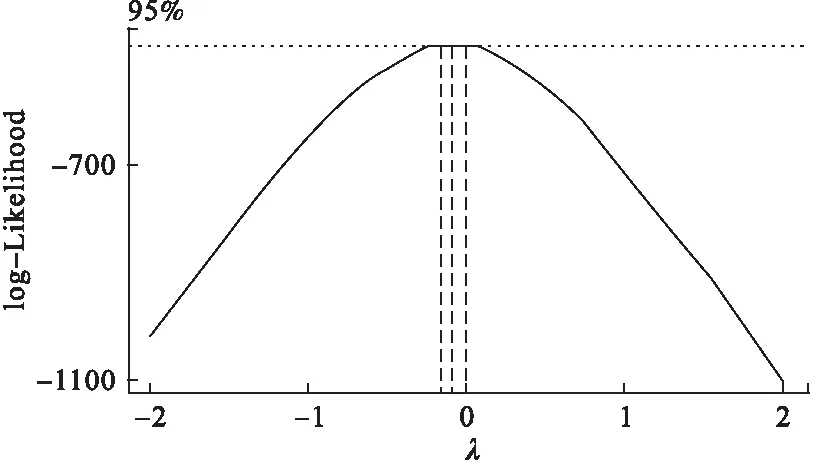
圖5 似然函數的最大值ln(Lmax(λ))隨λ變化的曲線

回歸方程的方差分析顯示,擬合的回歸方程有統計學意義(P<0.001)。對回歸系數進行假設檢驗,回歸系數也有統計學意義(P<0.001)。
(3) Box-Cox變換后建立的16種∑PAHs濃度與平均溫度回歸方程的回歸診斷
圖6為Box-Cox變換后建立的16種∑PAHs濃度與平均溫度的直線回歸方程的回歸診斷結果,結果顯示,Box-Cox變換后建立的回歸方程滿足正態性的假設,滿足方差齊性的條件。
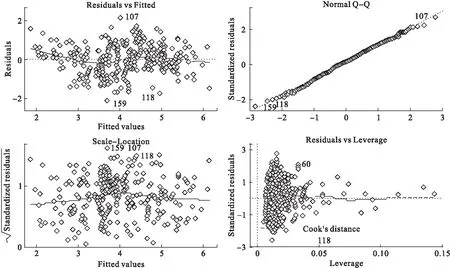
圖6 Box-Cox變換后16種∑PAHs濃度與平均溫度方程的回歸診斷
5.Box-Cox變換前后建立的回歸方程回歸分析結果比較
表2為 Box-Cox變換前后采用多元線性逐步回歸法和直線回歸法建立的回歸方程的回歸分析結果比較,結果顯示,經Box-Cox變換后,決定系數(R2)升高,對數據變換后建立的回歸方程的效果好于變換前建立的回歸方程。
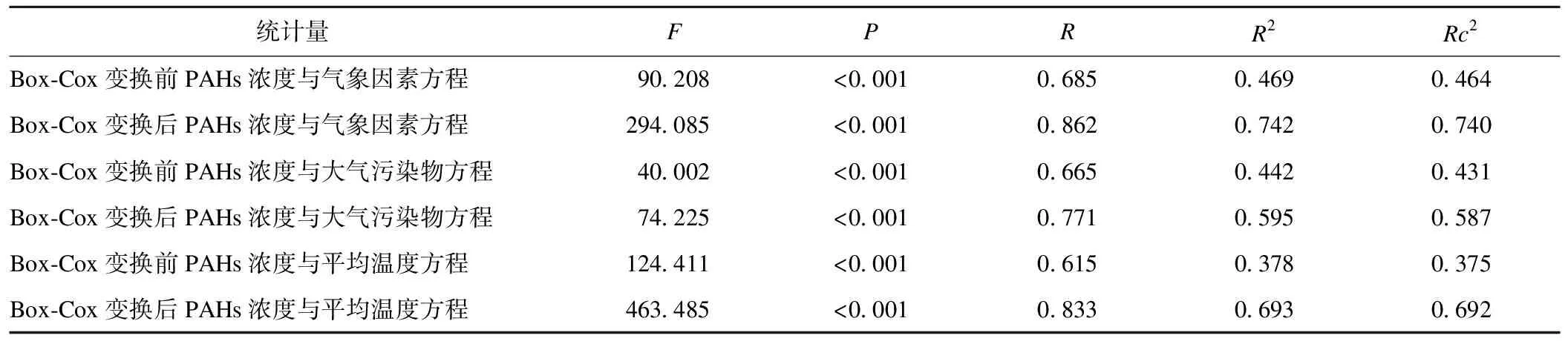
表2 Box-Cox變換前后建立的回歸方程的回歸分析結果比較
6.Box-Cox變換后建立的回歸方程預測值與實測值的比較
表3為Box-Cox變換后多元線性逐步回歸法和直線回歸法建立的回歸方程預測的2017年固定采樣日(每月10~16日)和霾日(AQI>200)的16種∑PAHs濃度與路北監測點實測的16種∑PAHs濃度的比較,經Kruskal-wallis H檢驗,P=0.154>0.05,按α=0.05檢驗水準,尚不能拒絕H0,差別無統計學意義,即Box-Cox變換后建立的方程預測的16種∑PAHs濃度與監測點實測的16種∑PAHs濃度均無差別。

表3 不同方程預測與實測的PAHs濃度的比較
討 論
16種∑PAHs濃度與平均溫度、風速和日照小時數之間呈負相關關系,與平均相對濕度和平均氣壓之間呈正相關關系,溫度高、日照時間長都會加速多環芳烴的分解,風速高會不利于多環芳烴的沉積[6],這與本研究16種∑PAHs濃度均與平均溫度、風速和日照小時數之間呈負相關關系結果一致。大氣中的PAHs主要以可吸入顆粒物和氣相的形式吸附在顆粒物或者在大氣飄塵中,空氣中的PAHs與氧氣、臭氧或其他氧化劑反應生成內環過氧化物[7]。PAHs濃度與PM2.5、PM10、SO2、NO2濃度呈正相關關系,與O3呈負相關結果一致。
將缺失變量16種∑PAHs濃度作為因變量,相關變量作為自變量,采用多元線性逐步回歸法和直線回歸法對因變量Y經Box-Cox變換前后擬合回歸方程。直線回歸方程顯示,大氣污染物中PM2.5對16種∑PAHs濃度影響最大;氣象因素中平均溫度對16種∑PAHs濃度影響最大[7]。研究表明,影響大氣中的 PAHs存在狀態的因素包括PAHs的理化性質、氣象因素、其他污染物(如PM10、SO2、NO2)等[8]。Callén等人利用多元線性回歸模型,用氣象因素和PM10濃度作為可能的預測指標能較好的模擬出空氣中PAHs濃度[9]。Mehmet等人也利用多元回歸分析預測PAHs與氣象因素和顆粒物濃度的關系,結果顯示,溫度對PAHs濃度影響較大,而相對濕度和氣壓影響相對較小,利用方程預測和實測的PAHs年均濃度相近,可以較好的說明多元回歸模型可用于PAHs濃度和相關因素的預測[10-11]。
對因變量Y經Box-Cox變換后采用多元線性逐步回歸法和直線回歸法預測得到2017年固定采樣日(每月10-16日)和霾日(AQI>200)的16種∑PAHs濃度與監測點實測的16種∑PAHs濃度進行比較,結果顯示,建立的方程預測的16種∑PAHs濃度與路北監測點實測的16種∑PAHs濃度均無差別。因變量Y經Box-Cox變換后采用多元線性逐步回歸法建立的回歸方程擬合效果優于Box-Cox變換前建立的回歸方程,而且采用多元線性逐步回歸法和曲線擬合法建立回歸方程較為簡單易行,可操作性強,能更直接的說明PAHS濃度與氣象因素和大氣污染物濃度之間的關系。因變量Y經Box-Cox變換后采用多元線性逐步回歸法擬合的PAHS濃度與平均溫度和風速的回歸方程效果較好(R2=0.742),能較好的預測16種∑PAHs濃度。可以用Box-Cox變換和多元線性逐步回歸法擬合16種∑PAHs濃度與平均溫度和風速的方程,然后用預測值來填補未監測日期的16種∑PAHs濃度。

