未來氣候模式下淮河流域極端降水量的時空變化分析

陳 琛，石 朋,2，瞿思敏，孫 龍，牟時雨，馮 穎，董豐成，崔彥萍

(1.河海大學水文水資源學院，江蘇南京210098；2.河海大學水文水資源與水利工程科學國家重點實驗室，江蘇南京210098；3.水利部信息中心，北京100053；4.江蘇省水文水資源勘測局江蘇南京210029)

在當前全球氣候變化的背景下，洪水、臺風、干旱以及雨雪冰凍等極端事件頻發，災害損失加劇，越來越多的人開始關注極端事件[1]。IPCC第五次評估報告指出，在多數陸地地區強降水事件發生的頻率呈增加趨勢[2]，觀測研究也表明，我國的極端強降水平均強度和極端降水值都有增加的趨勢[3]。為能準確預測極端降水變化情況，國內外眾多學者利用多種不同的極值分布類型對不同地區的極端事件進行研究，肖卉等[4]發現Pearson-Ⅲ型分布可以較好擬合江蘇省大暴雨分布特征，汪方等[5]證明了Gamma概率分布模型在降水擬合上有較好的擬合效果，張利平等[6]總結了不同極端水文事件中各分布函數的擬合效果。同時，也有學者對極端降水的變化情況做出研究，閔屾等[7]對極端降水的區域性和持續性特征做出了探究，表明不同地區的區域性和持續性特征各有差異，其中長江以南地區的區域性與持續性征均較大，容易誘發區域性洪水。

淮河流域位于中原地區，地跨河南、湖北、安徽、江蘇、山東5省，人口密集，降雨空間分布不均勻[8]，一旦發生洪澇事件將給當地居民的生命財產安全帶來極大危害，極端降水作為洪水的主要驅動因素，已引起眾多學者的廣泛關注。王麗萍等[9]發現1961年以來流域降水過程強度明顯增強,特強和強降水過程均明顯增多，劉暢等[10]對淮河流域極端降水的頻度和強度變化情況做出了分析。現有研究均著眼于過去極端降水變化，對未來氣候模式下的極端降水量變化研究還不多。本文在上述研究基礎上，基于小柳巷以上14個氣象站1960—2015年(共計55年)的逐日降水數據，選取英國Hadley氣候中心開發的HadGEM2-ES氣候模式，選取3種排放情景(RCP2.6、RCP4.5、RCP8.5)，使用delta統計降尺度方法預測未來60年該地區逐日降水量，結合統計特征，分析了未來氣候模式下淮河流域小柳巷以上區域的極端降水量時空變化規律。

1 數據與方法

1.1 研究數據

研究區及14個氣象站的分布情況見圖1，氣象數據均來自國家氣象信息中心http://data.cma.cn/。為保證研究結論的可靠性，首先對觀測資料進行了一致性檢驗，以排除由于臺站遷移、觀測儀器和方法變更等非氣象因素帶來的非均一性問題。本文利用Wijingaard等[11]提出的均一性檢驗方法，對14個氣象站的逐日降水觀測資料進行均一性檢驗，結果表明，所有站點資料均通過了95%置信水平下的顯著性檢驗。

圖1 淮河流域氣象站點分布圖Fig.1 Huaihe River Basin and location of meteorological stations

為規避只選取年最大值法會出現的遺漏有價值信息或混入無價值信息問題，對現有觀測數據和未來模擬數據，本文均同時考慮兩類極值序列，一類是年最值序列(Annual Maximum，AM)，另一類是超門限峰值序列(Peak over Threshold，POT)。POT序列的獲得很大程度上依賴于閾值的選擇，Reiss和 Thomas指出 Hill圖是尋找最優閾值的理想工具[12]，本文用Hill圖法選取最優閾值。經計算，本文選取日降水觀測資料超過99.5th分位點的數據組成待分析的POT序列。根據余敦先等[13]的研究結果，GEV(廣義極值分布)與GPD(廣義Pareto分布)為AM序列與POT序列的最優擬合。

1.2 分析方法

1) 極值分布模型與參數估計方法

廣義極值分布(GEV)與廣義Pareto分布(GPD)被廣泛應用于極值序列的擬合，已有研究表明，這兩種極值分布分別是淮河流域現有觀測資料AM序列與POT序列的最優分布[13]，故本文選取這兩種分布模型進行簡要介紹。

a) 廣義極值分布模型(GEV)

設X1,...,Xm是服從廣義極值分布的獨立隨機變量，則分布函數Fx(x)為：

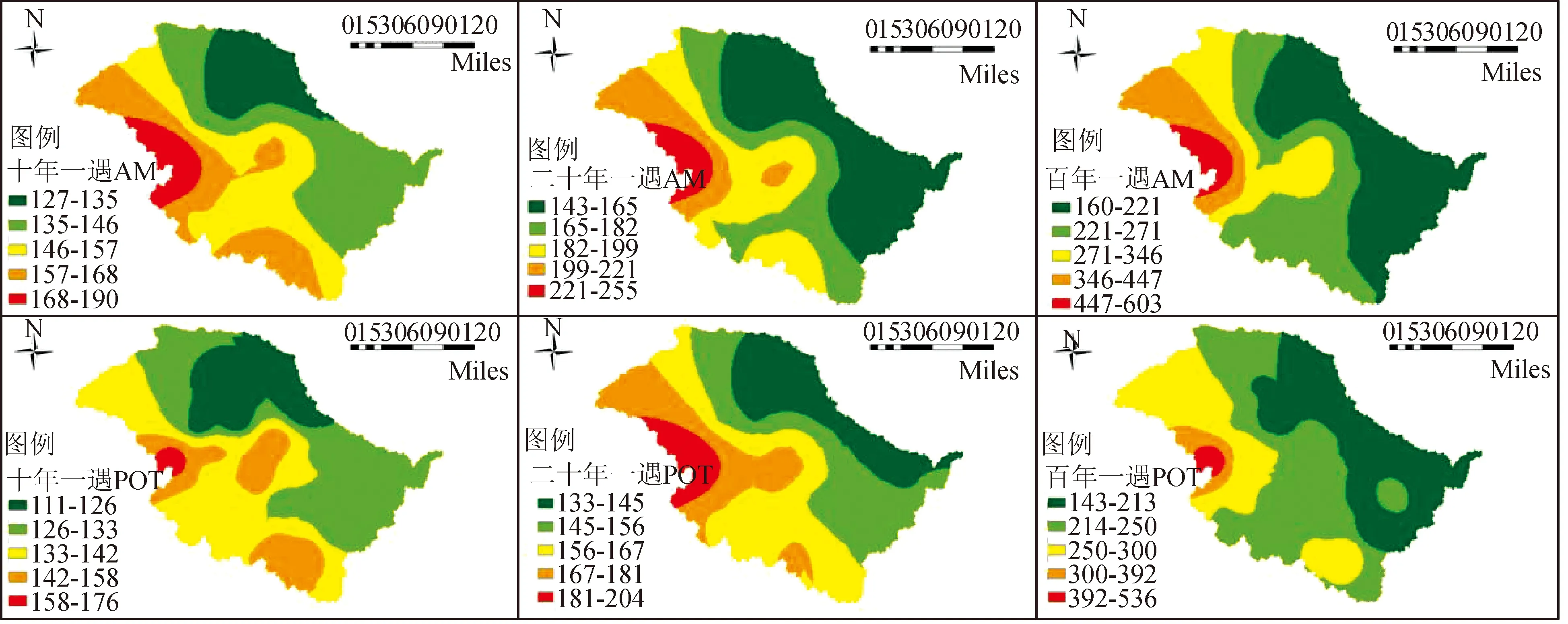
Fx(x)=P[X

(1)

式中：μ、σ、ξ分別為位置參數、尺度參數、形狀參數。位置參數μ∈R，尺度參數σ>0，形狀參數ξ∈R。μ=0,σ=1時稱為標準形式。

b) 廣義Pareto分布(GPD)

GPD的分布函數為：

(2)

式中：x是隨機變量，μ為門限值，σ為尺度參數，ε為形狀參數。

c) 參數估計方法

本文采用極大似然估計對以上2種分布參數進行估計，極大似然估計法對大樣本量的復雜模型有較好的適應性，與此同時，還可以得到分布的漸進分布、參數標準差和置信區間。

設{x1,x2,…,xn}為相互獨立且同分布的概率分布F(x),極大似然估計可通過下式求得：

(3)

使得上式值達到最大值的點即為相應參數的極大似然估計。

2)擬合優度檢驗方法

本文選取CVM檢驗(Cramér-von Mises test)來檢驗各分布的擬合效果，CVM檢驗是用來檢驗擬合優度的一種檢驗方法，對大小為n的順序統計量，定義統計函數

(4)

式中Fθ(x)是在參數為θ情況下，目標函數的累計分布函數。當ω2值大于臨界值時，拒絕原假設。

3) delta(CF)降尺度方法

第一步：估計GCM模擬基線和未來氣候的均值：

(5)

(6)

第二步：計算加法和乘法變化因子(CFadd、CFmul)：

(7)

CFmul=GCMf/GCMb

(8)

第三步：通過應用CFadd和CFmul獲得局部縮放的未來值(LSfadd,i和LSfmul,i)：

LSfadd,i=LObi+CFadd

(9)

LSfmul,i=LObi×CFmul

(10)

式中：LObi是在單個氣象站觀測到的氣象變量(在第i個時間步長中)的值，或者是指定時間域的流域的平均氣象時間序列。LSfadd,i和LSfmul,i是用CFM的加性和乘法公式得到的變量未來情景的值。

2 結果分析

未來氣候模式，是通過控制溫室氣體的排放，運用氣候系統模式來對未來氣候情景做出定量的描述。IPCC第四次報告中將溫室氣體排放劃分為高(A1)中(A1B)低(B1)三種模式。在IPCC第五次報告中，為了更好地將排放與社會經濟情景有機結合，從而更好地模擬出未來氣候變化對區域的影響，開發出新的情景模式(RCPs)[14]。本文選取英國Hadley氣候中心開發的HadGEM2-ES氣候模式，模式模擬精度為1.88°×1.25°，選取3種排放情景(RCP2.6、RCP4.5、RCP8.5)(數字越大代表人類社會活動對流域影響越大)，使用delta統計降尺度方法預測未來60年該地區逐日降水量。

GEV分布和GPD分布分別為淮河流域現有觀測數據AM序列與POT序列的最優擬合分布。為判斷GEV分布與GPD分布是否仍可以較好模擬未來氣候模式下流域降水量的AM序列與POT序列，使用CVM檢驗對兩種序列對應的分布進行檢驗。檢驗結果見表1，CVM檢驗值越趨近于1，則擬合效果越好，表中檢驗值絕大多數大于0.5，即GEV分布與GPD分布仍可較好擬合三種排放情景下淮河流域的AM序列與POT序列。

將1960—2075年劃分為3個年代際，分別是1960—2015年、2016—2045年、2046—2075年，計算各年代際間極端降水均值并表示在空間圖中，以觀察不同年代際間、不同排放情景下淮河流域極端降水暴雨中心是否發生明顯變化，見圖2～4。

表1 2016—2075年AM序列與POT序列CVM檢驗值Tab.1 Value of CVM test of AM series and POT series during 2016—2075

圖2 RCP2.6，1960—2015年、2015—2045年、2046—2075年AM序列與POT序列暴雨中心分布圖Fig.2 Rainstorm center of AM series and POT series during 1960—2015,2015—2045,2046—2075 under RCP2.6

圖3 RCP4.5，1960—2015年、2015—2045年、2046—2075年AM序列與POT序列暴雨中心分布圖Fig.3 Rainstorm center of AM series and POT series during 1960—2015,2015—2045,and 2046—2075 under RCP4.5

圖4 RCP8.5，1960—2015年、2015—2045年、2046—2075年AM序列與POT序列暴雨中心分布圖Fig.4 Rainstorm center of AM series and POT series during 1960—2015,2015—2045,and 2046—2075 under RCP8.5

從圖2～4可以看出，在RCP2.6、RCP4.5、RCP8.5三種排放情景下，各年代際間的極端降水最大值仍集中在流域南部，年代際間暴雨中心都未發生明顯偏移，均分布在淮河流域上游(信陽站、霍山站一帶)。從數值來看，在三種排放情景下，未來60年極端降水均值相比于現在略有增長，但2016—2045年與2045—2075年兩個年代際間相比，未發生明顯變化，相同年代際間，AM序列略大于POT序列。三種排放情景之間相比，RCP8.5極端降水均值增長最為明顯，在2045—2075年間，RCP8.5下AM序列的極端降水最大值152.5 mm，RCP2.6中為123.1 mm，兩者相差29.4 mm，增長約23.9%。由以上結果可以看出，在未來氣候模式下，淮河流域暴雨中心雖未發生明顯偏移，但極端降水量有增大趨勢，且隨人類活動對流域影響的增大而增大。

對未來氣候模式下AM序列與POT序列，分別用GEV分布與GPD分布計算重現期。

圖5～7表明，在三種排放情景下，淮河流域AM序列與POT序列十年一遇、二十年一遇與百年一遇的降水量空間分布基本相同，降水極大值多發生于淮河上游。而從數值上看，RCP2.6、RCP4.5、RCP8.5三種排放情景下，相同序列、相同重現期的降水量數值依次增大。

重現期與事件發生的概率相對，重現期越長，則事件發生的概率越小，對應的降水量越大，這與不同重現期下AM與POT序列模擬的降水量分布數值是相對應的，同時可以發現，在相同排放情景、相同重現期情況下，AM序列模擬數值普遍大于POT序列，這與現有實測資料AM序列與POT序列均值的比較結果相吻合。

圖5 RCP2.6，AM序列與POT序列重現期分別為10a、20a、100a時的降水量分布圖Fig.5 Precipitation distribution of AM series and POT series in reappearing periods of 10a,20a,100a under RCP2.6

圖6 RCP4.5，AM序列與POT序列重現期分別為10a、20a、100a時的降水量分布圖Fig.6 Precipitation distribution of AM series and POT series in reappearing periods of 10a,20a and 100a under RCP4.5

圖7 RCP8.5，AM序列與POT序列重現期分別為10a、20a、100a時的降水量分布圖Fig.7 Precipitation distribution of AM series and POT series in reappearing periods of 10a,20a and 100a under RCP8.5

3 結 論

本文以淮河小柳巷以上流域14個氣象站1960—2015年逐日降水數據為基礎，模擬不同排放情景下研究區2016—2075年逐日降水過程，通過統計分析，研究淮河流域未來不同排放情景下極端降水的時空變化特征，得出結論。

1) 3種排放情景下，未來60年淮河流域暴雨中心未發生重大偏移，暴雨中心仍將集中于淮河上游(信陽站、霍山站一帶)，將給該地區帶來潛在的防洪壓力；同時3種模式下極端降水數值都略有增加，增加數值隨著人類活動對流域的影響增大而增大。

2) 計算重現期為10年、20年與100年下的極端降水，兩種序列空間分布情況一致，降水分布均為南多北少，極值中的最大值均分布在流域上游，隨著重現期的延長，極端降水數值增大，且隨著人類活動影響增大而增大。

3) 在相同排放情景，相同重現期下AM序列的極端降水數值要略大于POT序列，這與現有實測資料AM序列與POT序列均值的比較結果一致。