軸向磁場作用下Czochralski淺液池內熱對流特性研究
高 鍵,彭 嵐,馬 力,朱承志
(重慶大學動力工程學院,低品位能源利用技術及系統(tǒng)教育部重點實驗室,重慶 400044)
1 引 言
在Cz法制備晶體的過程中,熔體在溫差梯度作用下會產生表面張力梯度,形成Marangoni-熱毛細對流。當溫差梯度超過某一臨界值后,熔體流動將轉變?yōu)榉欠€(wěn)態(tài)振蕩流動,其會使晶體的均勻性受到破壞、影響晶體材料的生長質量[1]。近幾十年來,學者們對不同工質[2-3]、不同幾何模型[4-5]、不同邊界條件[6-8]下的熔體對流運動進行了大量的研究,得到了熱毛細對流的演變規(guī)律,并分析和解釋了相應的物理機制。Teitel等[9]對Cz液池內流動不穩(wěn)定性進行了研究,考慮不同內外徑之比對流動的影響,發(fā)現(xiàn)增大內外徑之比可以減小臨界溫差。Peng等[10]對Cz淺液池內硅熔體的熱對流過程進行了深入的研究,發(fā)現(xiàn)隨著徑向溫差的不斷增大,流動會發(fā)生由穩(wěn)態(tài)流動向非穩(wěn)態(tài)流動的轉變,并確定了流型轉變的臨界條件。
施加外部磁場是抑制熔體熱對流的一種行之有效的方法。Virbulis等[11]采用二維軸對稱模型,研究了穩(wěn)態(tài)磁場、交變磁場和復合磁場對熔體對流對界面形狀的影響,并與實驗數據進行了比較。Ozoe等[12]對磁場作用下矩形池內的熱對流進行了三維數值模擬,研究結果表明:磁場方向對熔體的對流運動具有較大的影響,當外加磁場方向垂直于豎直邊界層時,抑制效果最強;而當外加磁場方向平行于豎直邊界層時,抑制效果最弱。Takagi等[13]研究了在水平溫差作用下,坩堝旋轉和軸向磁場對熔體熱毛細對流的影響。結果發(fā)現(xiàn):單獨施加磁場和同時施加磁場和旋轉均對流動具有較好的抑制作用。
目前對磁場作用下熔體熱對流的研究主要集中在由單向水平溫差引起的流動,而在Cz法生長單晶硅的過程中,由于熔體溫度較高,易與外界進行輻射換熱、引起散熱損失;同時,生產中對坩堝底部進行加熱,均會導致垂直自由表面方向產生相當大的溫差梯度[14]。故在實際工程應用中,雙向溫差梯度往往同時存在,共同驅動流體進行運動。因此,本文采用數值模擬方法對Cz液池內Marangoni-熱毛細對流進行研究,保持底部熱流密度恒定,主要討論了軸向磁場對臨界水平溫差Macri、穩(wěn)態(tài)流動和非穩(wěn)態(tài)流動的影響。
2 物理數學模型
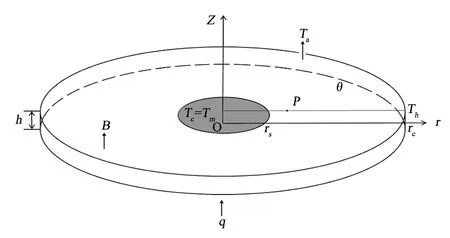
圖1 物理模型Fig.1 Configuration of system
物理數學模型如圖1所示,晶體半徑rs=15 mm,坩堝半徑外徑rc=50 mm,圓柱形坩堝半徑內充滿了深度h=3 mm的硅熔體。坩堝側壁和熔體-晶體界面分別維持恒定溫度Th和Tc,水平溫差ΔT=Th-Tc。熔體表面與外界進行輻射換熱(環(huán)境溫度:Ta)。坩堝底部以均勻的熱流密度q進行加熱,并沿Z軸正方向施加磁場強度為B的靜態(tài)磁場。
為簡化計算,作以下假定:(1)熔體流動速度較低,可考慮為層流;(2)熔體為不可壓縮牛頓流體;(3)除自由表面以外,其他界面均滿足貼壁無滑移條件;(4)自由表面考慮熱毛力作用,其與溫度滿足線性關系;(5)邊界都為電絕緣。
根據上述假設,無量綱化基本方程如下:
▽·V=0
(1)
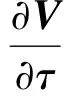
(2)

(3)
式(2)中F為洛倫茲力,其無量綱分量如下:
(4)
(5)
FZ=0
(6)
其中,φ為電勢,滿足下列方程式:
▽2φ=▽·(V×B)
(7)
無量綱化邊界條件為:
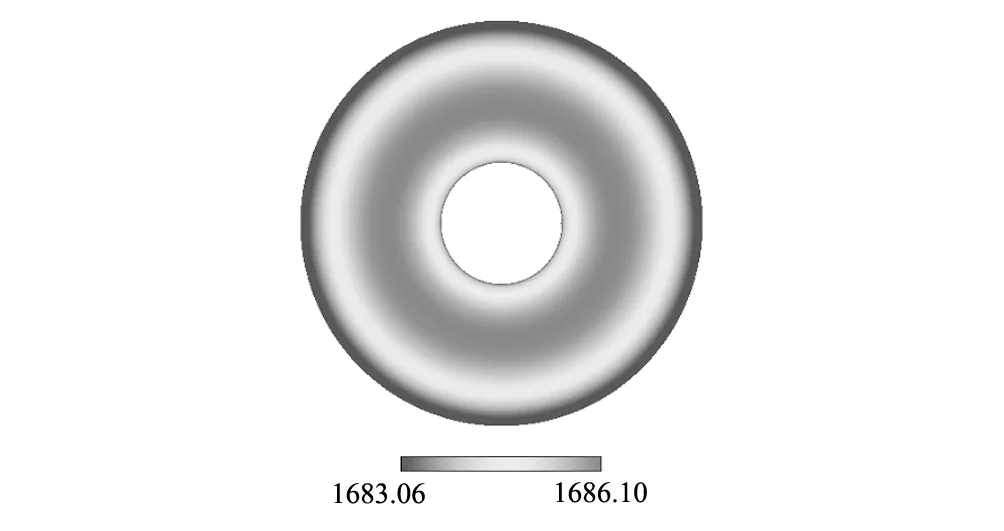
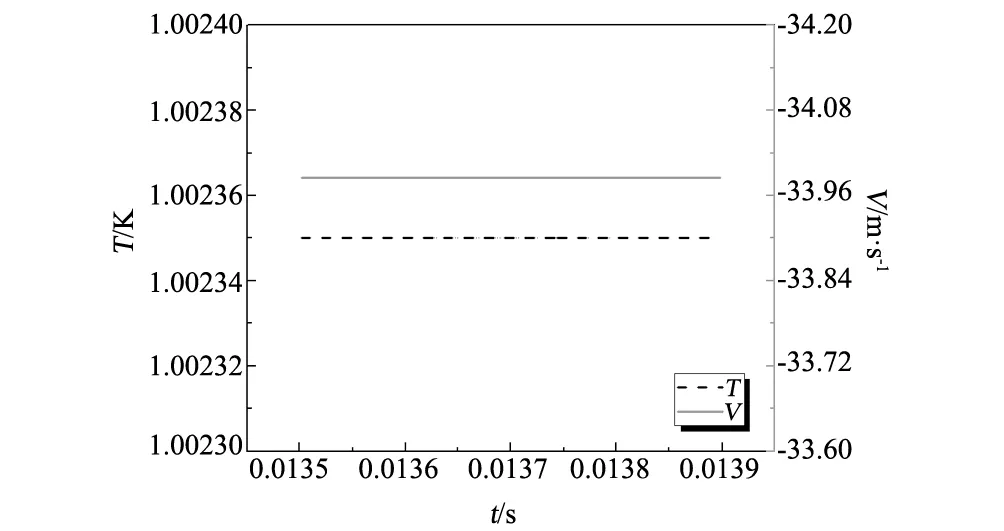
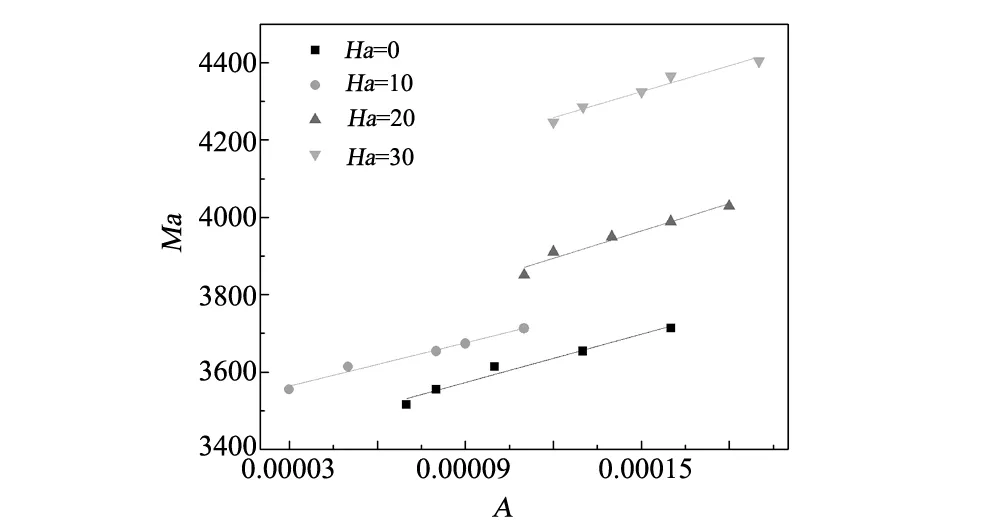
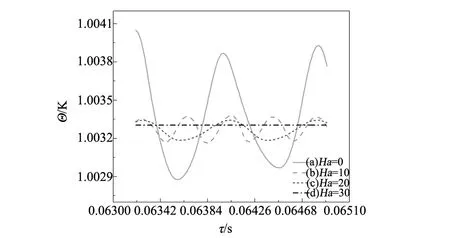
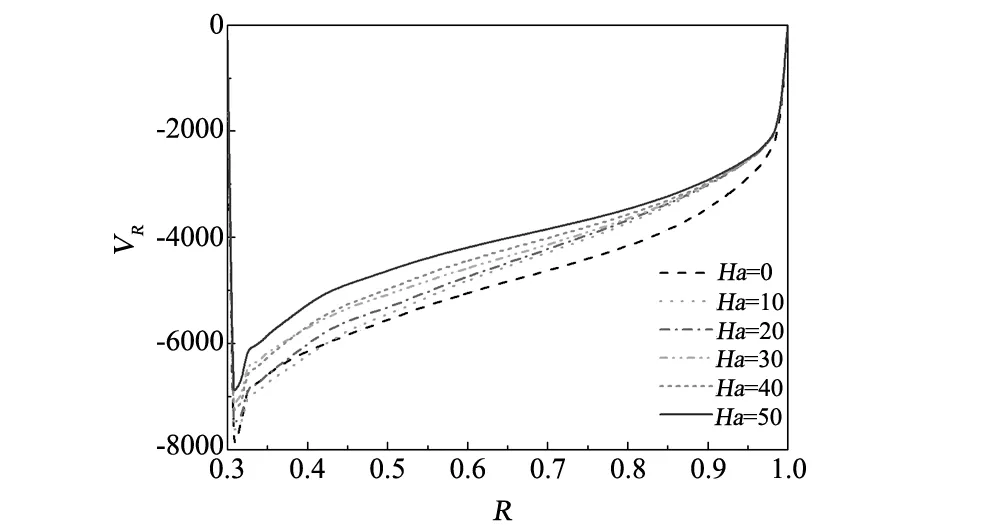
自由表面(Z=h/rc,rs/rc (8) 液池底部(Z=0,0 (9) 熔體-晶體界面(Z=h/rc,0 (10) 坩堝側壁(0 (11) 利用有限容積法對控制方程進行離散,壓力插值采用PRESTO格式,對流項為QUICK格式,擴散項為中心差分格式,壓力-速度修正采用PISO算法,程序的正確性驗證參閱文獻[14]。在Ma=1185,Q=1.5705×10-2工況下分別對不同大小的網格進行了計算,結果如表1所示,采用80R×120θ×40Z非均勻交錯網格。 表1 網格無關性檢驗Table 1 Grid independent test 由于硅熔體熔點溫度較高,易與外界環(huán)境進行輻射換熱。為了避免因熱量損失導致硅熔體溫度下降而形成結晶,在坩堝底部施以恒定熱流密度對熔體進行加熱。圖2給出了底部熱流為Q=1.3461×10-2(q=3 W/cm2)時自由表面溫度分布情況。此時,熔體的最低溫度不低于晶體的熔點溫度1683 K,確保了物理模型的合理性。故本文保持底部熱流密度恒定(即Q=1.3461×10-2),重點考察磁場強度和水平溫差梯度對熔體傳熱和流動過程的影響。 當水平溫差較小時,液池內硅熔體的流動將保持軸對稱穩(wěn)定狀態(tài),這種流動被稱為基本流。圖3 給出了Ma=2370(ΔT=12 K)時,自由表面監(jiān)測點P處溫度和速度隨時間的變化關系,此時監(jiān)測點溫度和速度都不隨時間而變化,熔體內Marangoni-熱毛細對流為穩(wěn)態(tài)流動狀態(tài)。為了進一步了解磁場強度對這種穩(wěn)態(tài)流動的影響,定義自由表面溫度波動δΘ為: 圖2 Ma=0(ΔT=0 K),Q=1.3461×10-2時,自由表面溫度分布Fig.2 Ma=0,Q=1.3461×10-2,free surface temperature distribution 圖3 Ma=2370(ΔT=12 K),Qmin=1.3461×10-2時,監(jiān)測點P處溫度和速度變化Fig.3 Ma=2370,Qmin=1.3461×10-2,variations of temperature and velocity at the monitoring point P 圖4給出了不同Ha數下自由表面溫度波動情況。當磁場強度較低時(0≤Ha≤20),此時Ha值較小,波型結構保持不變,為直條幅波;當磁場強度增加到Ha=30時,磁場對流動結構具有顯著的抑制效果,波型由直條幅波演化成橢圓狀波,波數由12減少到4;隨著磁場強度進一步增大(40≤Ha≤50),由于此時流動強度已十分微弱,導電流體在磁場作用下產生與流動方向相反的洛倫茲力,其數值也相對較小,磁場對流動的抑制效果逐漸減弱,自由表面溫度波動結構和波數不再發(fā)生變化。 圖4 Ma=2370(ΔT=12 K),Q=1.3461×10-2時,不同Ha數下自由表面溫度波動情況Fig.4 Ma=2370, Q=1.3461×10-2, free surface temperature fluctuation 隨著水平溫差不斷增大,液池內硅熔體流動強度將進一步加劇。當Ma超過臨界Macri時,流動會發(fā)生失穩(wěn),此時監(jiān)測點P處的溫度可呈現(xiàn)出周期性的等幅振蕩,如圖6(b)所示。一個振蕩周期內最高溫度和最低溫度的差值即為溫度振幅,其與Ma呈近似的線性關系[15]。利用線性外推法可確定不同磁場強度作用下流動轉變的臨界Macri。圖5給出了當底部熱流Q=1.3461×10-2,Ha數分別為0、10、20和30時,監(jiān)測點P處的無量綱溫度振幅A與Ma數之間的變化規(guī)律。 表2給出了相應條件下臨界Macri和線性擬合公式。可以看出,在保持底部熱流密度恒定的情況下,隨著軸向磁場不斷增強,臨界Macri不斷增加且變化幅度愈來愈大,說明軸向磁場的引入會提高Marangoni-熱毛細對流的穩(wěn)定性。 表2 Q=1.3461×10-2時不同Ha數下的臨界水平溫差MacriTable 2 Critical Ma with different Ha when Q=1.3461×10-2 圖5 Q=1.3461×10-2時不同Ha數下監(jiān)測點P處溫度振幅A與水平溫差Ma的關系Fig.5 Change of the temperature amplitude A with Ma at the point P for different Ha when Q=1.3461×10-2 圖6 Ma=3950(ΔT=20 K),Q=1.3461×10-2時,不同Ha數下監(jiān)測點P處溫度變化Fig.6 Ma=3950, Q=1.3461×10-2, temperature evolution at the monitoring point P for different Ha 圖7 Ma=3950(ΔT=20 K),Q=1.3461×10-2時,不同Ha數下自由表面溫度波動情況Fig.7 Ma=3950, Q=1.3461×10-2, free surface temperature fluctuation 由表2可知,在沒有軸向磁場的作用下,當Ma>3385.3時,流動為非穩(wěn)態(tài)振蕩對流。為了研究軸向磁場對非穩(wěn)態(tài)流動的影響,對水平溫差Ma=3950(ΔT=20 K)時,不同Ha數下的熔體流動進行了一系列數值模擬。圖6給出了自由表面監(jiān)測點P處溫度隨時間的變化情況,從圖中可以看出:當磁場強度為零時(Ha=0),溫度振蕩混亂而無規(guī)律;隨著磁場強度不斷增大(10≤Ha≤20),溫度呈現(xiàn)規(guī)律的等幅振蕩,但流動仍保持三維非穩(wěn)態(tài)狀態(tài);當Ha=30時,此時Ma數已小于對應磁場強度下的臨界Macri,溫度振幅減小至零,流動由非穩(wěn)態(tài)轉變?yōu)榉€(wěn)態(tài)。 圖7所示為Ma=3950時,不同磁場強度下自由表面的溫度波動圖。當未施加軸向磁場時(Ha=0),自由表面溫度波動為一種典型的熱流體波,呈現(xiàn)出彎曲的輪輻狀;引入軸向磁場后(10≤Ha≤20),流動的不穩(wěn)定性逐漸減弱,溫度波動由原來的熱流體波轉變?yōu)椴鏍罱Y構;當Ha=30時,自由表面呈現(xiàn)出明暗相間的直條紋,波動結構由三維非穩(wěn)態(tài)流動過渡為三維穩(wěn)態(tài)流動,波數m=11;隨著磁場強度進一步增大(40≤Ha≤50),此時磁場對流動的影響較小,與圖4中的計算結果類似,溫度波動結構基本保持不變,但自由表面波數先減小后增大。 圖8 Ma=3950(ΔT=20 K),Q=1.3461×10-2時,不同Ha數下自由表面徑向速度分布Fig.8 Ma=3950,Q=1.3461×10-2,radius velocity distributions on free surface 圖8給出了Ma=3950時,不同磁場強度下自由表面熔體徑向速度分布圖。從圖中可以看出,最大無因次徑向速度出現(xiàn)在靠內壁面附近。隨著磁場強度的不斷增加,徑向速度沿徑向分布的非線性程度不斷減弱,速度分布曲線愈加平緩。當Ha=0時,最大無因次徑向速度為7490.67;而Ha=50時,最大無因次徑向速度為6850.74,最大無因次徑向速度隨著磁場強度的增加而不斷減小,表明洛倫茲力對熔體流動的具有顯著的抑制效果。 表3給出了水平溫差Ma=2370、3950(ΔT=12 K 、20 K),熔體在Ha數為0、10、20、30、40、50下,自由表面最大溫度波動值。從表中可以看出,軸向磁場對穩(wěn)態(tài)和非穩(wěn)態(tài)Marangoni-熱毛細對流均有抑制作用,當磁場強度Ha=30時,自由表面最大溫度波動值呈數量級遞減,此時磁場對流動的抑制效果最為明顯。隨著磁場強度進一步增大(40≤Ha≤50),自由表面最大溫度波動值變化幅度逐漸減弱,這是因為此時熔體流動已較為微弱,磁場對流動的抑制效果也逐漸減弱,這與圖4和圖7中自由表面溫度波型結構的演變過程相吻合。同時也可以看出,在磁場強度保持一定的情況下,隨著水平溫差梯度的增加,自由表面最大溫度波動值不斷增大,熔體內部流動也更為劇烈。 表3 不同Ha數下Ma=2370、3950時自由表面最大溫度波動值Table 3 Maximum temperature fluctuation value with different Ha when Ma=2370, 3950 本文采用三維數值模擬方法研究了軸向磁場對雙向溫差作用下Czochralski淺液池內Marangoni-熱毛細對流的影響,主要討論了軸向磁場對臨界Macri、穩(wěn)態(tài)流動和非穩(wěn)態(tài)流動的影響,結果表明: (1)在底部熱流密度恒定的情況下,確定了不同Ha數下流動由三維穩(wěn)態(tài)向三維非穩(wěn)態(tài)轉變的臨界Macri。隨著Ha數的增大,臨界Macri不斷增大,軸向磁場的引入會增強Marangoni-熱毛細對流的穩(wěn)定性。 (2)軸向磁場對液池內穩(wěn)態(tài)和非穩(wěn)態(tài)Marangoni-熱毛細對流均具有較好的抑制效果。對于穩(wěn)態(tài)流動,磁場的引入會使自由表面溫度波動幅值受到削弱,波數減少;對于非穩(wěn)態(tài)流動,隨著磁場強度的不斷增加,監(jiān)測點P處的溫度振蕩逐漸減弱直至消失,流動由三維非穩(wěn)態(tài)轉變?yōu)槿S穩(wěn)態(tài),自由表面溫度波動結構發(fā)生顯著變化,波動幅值逐漸下降。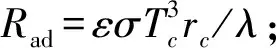

3 結果與討論
3.1 軸向磁場對穩(wěn)態(tài)流動的影響

3.2 軸向磁場對臨界Macri的影響


3.3 軸向磁場對非穩(wěn)態(tài)流動的影響

4 結 論

