基于PCA和AP的嵌套式KNN金融時間序列預測模型
, ,
(1.西南財經大學 天府學院 智能金融學院,四川 成都 610052; 2.成都大學 商學院,四川 成都 610106; 3.重慶金融學院 智能金融研究中心,重慶 400067)
1 引言
金融時間序列預測是一個極具挑戰性的理論和技術問題,具有重要的經濟意義,近年來引起了金融界和計算機界的廣泛關注。金融時間序列概率可預測性已被大量文獻所證實。在有效市場假說(EMH)的基礎上,Box和Jenkins[1]提出了ARIMA模型,Engle[2]提出了ARCH模型,Bollerslev[3]提出了GARCH模型,認為金融市場的價格波動有可預測性,但并非是價格本身。而一些跨學科的研究人員采用從其他不同角度繼續研究金融市場預測,包括常見的混沌理論模型[4],支持向量機(SVM)的預測模型[5],神經網絡(NN)的預測模型[6],和基于k-最鄰近元(KNN)的預測模型[7]。
在這些常用的預測模型中,Cover和Hart[8]提出的KNN可以處理高維數據,并能夠簡單直觀地從特征空間中提取相似實例進行預測分析,由此被廣泛應用于時間序列預測[9]。但是KNN有兩個明顯的缺陷會影響其性能也是眾所周知的。第一,計算量過大,因為需要計算測試點與已知樣本中的所有點的相似度,并找到k個最鄰近元;第二,受不均衡樣本影響,當不同類所含樣本點數量差距較大時,測試點的k個最鄰近元中,大樣本類容易占多數而影響測試點的分類或者回歸效果。為了解決這兩個問題,本文提出了一種嵌套式KNN,稱為Nested KNN。Nested KNN分成兩層:第一層首先計算預測點前一時點t與各個聚類中心的相似度,并找到其最近的聚類中心和相應的聚類;第二層計算t與第一層輸出的聚類中的各個點的相似度,并找到t的k個最鄰近元。由于第一層只需要計算t與各個聚類中心的相似度,所以大大減少了算法的計算量;第二層只計算t與同一聚類中的各個點的相似度,因此避免了受不均衡樣本的影響。
Tsai和Hsiao[10]指出特征提取是金融時間序列預測的關鍵。本文采用主成分分析(PCA)和仿射傳播聚類(AP)對歷史數據集進行特征提取,將輸出的特征作為Nested KNN預測的輸入。由此提出了一種將PCA、AP和Nested KNN組合起來的智能預測模型,簡稱為PANK模型(PCA+AP+Nested KNN)。該模型將用于實證預測歐元兌美元匯率及滬深300指數的走勢。
2 PANK預測模型的結構框架
本文在KNN回歸的基礎上,提出了PANK金融時間序列預測模型。PANK模型通過PCA來減少原始金融時間序列中的冗余信息,生成富含有效信息的主成分,并將其輸入AP進行聚類以找到時間序列的最優聚類方案和相應的聚類中心集,最后輸入兩層嵌套式Nested KNN進行回歸預測。
一般地,我們取一段足夠長的歷史數據對模型進行訓練和測試。首先,需要確定數據的時間框架,本文采用日數據,用日作為基本時間尺度。時間序列X(t)表示t時間(一天)的數據,包含了四個價格分量:開盤價X.O(t)、最高價X.H(t)、最低價X.L(t)、收盤價X.C(t)和交易量X.V(t)。在本文中,我們只考慮X.C(t),因此在后面的論述中X(t)僅包含X.C(t),在后續研究中我們將會加入更多的分量。
對于任意X(t),定義當日相對收益率
(1)
其中λ表示預測步長,最基本預測步長為1,因此在沒有具體說明時,本文用RR(t)表示RR(t,λ)。取足夠長的歷史相對收益率數據
DR(t,T)=(RR(t),RR(t-1),…,
RR(t-(T-m)+1))
(2)
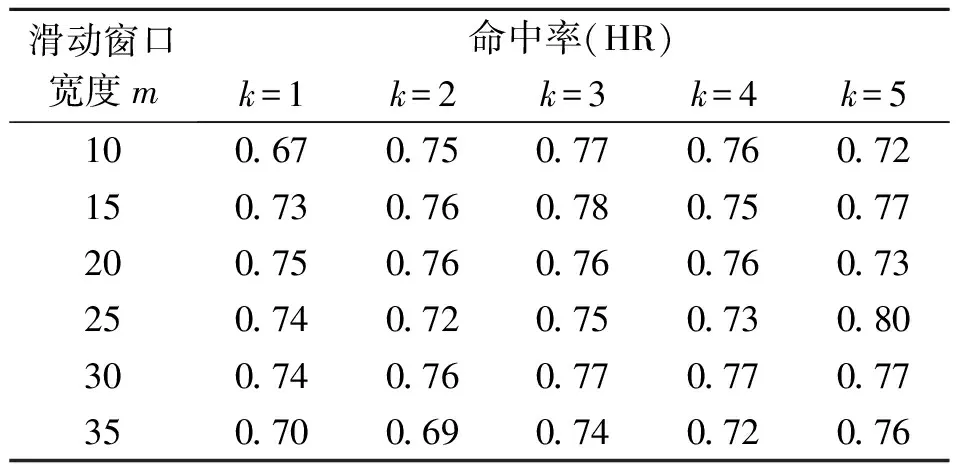
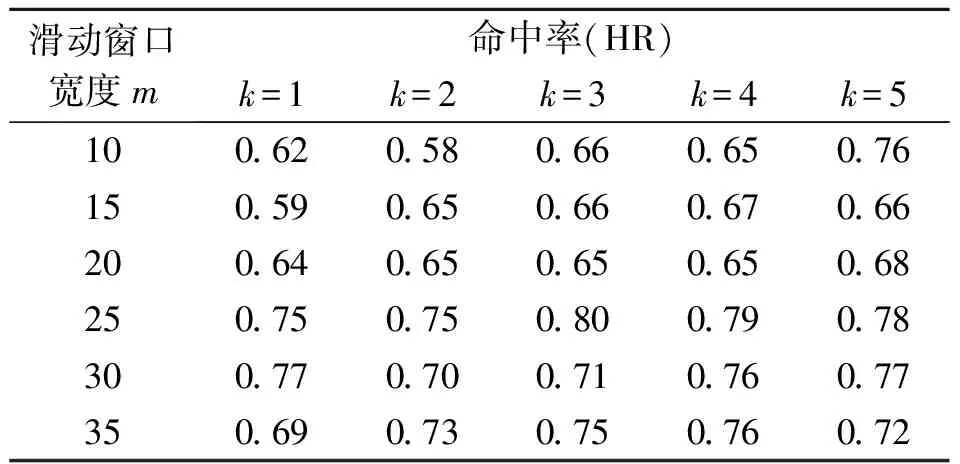
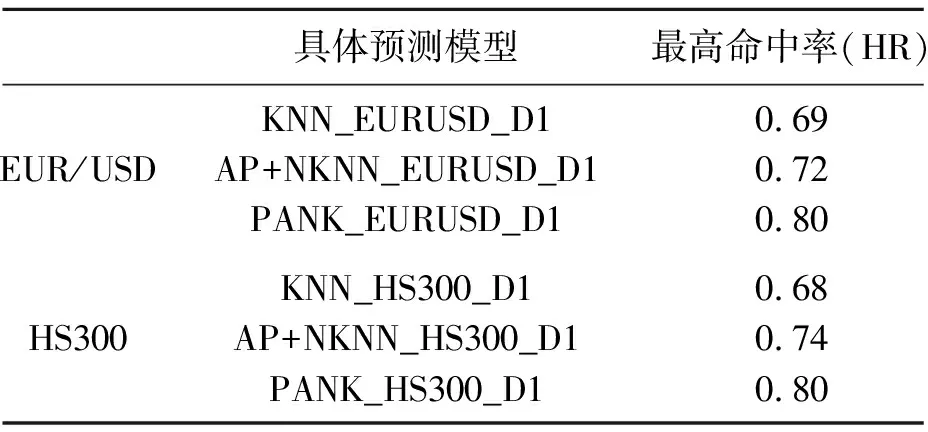
其中t表示所取得的數據中最近的時間點;T表示全部數據的總天數;m< 一般的PANK預測模型可以表達為 PANK:RR(t+λ)=NKNN(C(t),k) (3) 其中NKNN表示嵌套式KNN;C(t)是AP聚類后生成的最優聚類結果,是預測模型提取的特征集;k是模型參數;RR(t+λ)是模型輸出的預測日的相對收益率。具體地,PANK模型使用PCA和AP聚類生成特征集C(t),因此,PANK模型可以進一步地表達為 PANK:RR(t+λ)=NKNN{FE[AP(PCA(DR(t,m)))],k} (4) 其中FE( )(Feature Extraction, FE)表示聚類提取特征值的過程。 PANK模型由PCA、AP和Nested KNN三個部分組成。模型首先采用PCA提取富含原始數據信息的主分量,并輸入AP進行信息傳播聚類,生成特征集C(t),最后輸入Nested KNN進行回歸預測。下面將依次介紹PANK模型的各個組成部分及其算法流程。 主成分分析(Principal Component Analysis, PCA)是1901年由Pearson提出并于1933年由Hotelling發展[11,12],是一種常用的減少冗余信息,對大數據進行降維的方法。在應用PCA提取主分量之前,需要采用滑動窗口(窗口寬度為m)技術截取歷史數據[13],形成預測模型的輸入,并形成預測模型訓練輸入輸出數據集 DT(t,T-m)={D→R} (5) D=(DR(t-1,m)DR(t-2,m)…DR(t-(T-m),m))′ (6) R=(RR(t)RR(t-1)…RR(t-(T-m)+1))′ (7) PANK模型的第一步是PCA變換減少冗余數據,獲取主分量,這實際也是一個奇異值分解過程。首先對歷史數據矩陣D進行標準化處理和奇異值分解,可得矩陣Z Z=UΣVT (8) 其中U和V都是正交矩陣,分別是ZZT和ZTZ的特征向量矩陣。Σ是非負矩形對角矩陣,其左上角的子矩陣的對角元素λi(i=1,2,…,r)為ZZT的特征值。由此可以得到數據轉換矩陣 P=ZTU=VΣTUTU=VΣT (9) 其中矩陣P的各列依次為各個主成分。 實際上,在時間序列組成的矩陣中,存在信息冗余,其信息主要集中于前面部分主分量上。因此,我們可根據對主成分累積貢獻率(Cumulative Contribution Rate, CCR)的約束來提取前l(l< (10) 仿射傳播聚類(Affinity Propagation, AP)是2007年Frey和 Dueck[14]在Science上提出的一種快速有效的新聚類算法,該算法事先將所有的數據點都看作是可能的聚類中心,通過不斷的循環迭代,最終獲得包含有一系列聚類中心和相應的聚類集的聚類方案。在含有N個數據點的樣本中,AP算法首先計算每兩個數據點之間的相似度,并組成相似度矩陣SN×N。在此基礎上,每個數據點都被看作是潛在的聚類中心(稱為exemplar),然后通過迭代循環,在信息的搜集和傳遞過程中不斷競爭,最后產生一系列最優的聚類中心,并將各個數據點分配到最相似的聚類中心所代表的類中,形成AP最優的聚類結果[14]。下面將具體說明AP的算法流程。 在金融時間序列經過PCA后,將選出的主成分組成樣本空間,計算每兩個樣本點i和j之間的相似度S(i,j)。在本文中,以歐氏距離作為相似度測度,后續的研究中將探索更適合金融時間序列相似度的測度方法,有 S(i,j)=-‖i-j‖2 (11) 同時生成了由所有的相似度S(i,j)組成的相似度矩陣S。 為了找到最合適的聚類中心,AP算法在相似度矩陣S的基礎上,對每個樣本點進行信息搜集和傳遞,并進行迭代循環。在每一個迭代循環過程中,對于任意一個潛在的聚類中心e,都從任意一個樣本點i搜集信息R(i,e),同時,也為點i從潛在的聚類中心e搜集信息A(i,e) (12) (13) 其中R(i,e)表示點e對點i的吸引度(responsibility)或者說是點e適合作為點i的聚類中心的程度。A(i,e)表示點i對點e的歸屬度(availability)或者說是點i選擇點e作為其聚類中心的適合程度。整個過程中R(i,e)和A(i,e)不斷被計算迭代直到R(i,e)+A(i,e)達到最大值,點e才是選出來的最適合點i的聚類中心。 需要指出的是,在相似度矩陣的對角線上存在非常重要的偏向參數p,它表示每個點被選作聚類中心的傾向性。一般地,設定p的初始值pm為相似度矩陣S中元素的中值,下降步幅[15] (14) 在迭代循環的過程中,若聚類個數收斂到某個值h時,以pstep逐漸減小p,并繼續迭代,以獲得不同聚類個數的不同聚類方案。為了在不同的聚類方案中,選取一個最優的,可引入能夠有效反映聚類結構中的類內緊密性和類間分離性的Silhouette指標[15]。假設樣本空間被分成了r個聚類Ci(i=1,2,…,r),可以計算點x*的Silhouette指標 (15) 其中d(x*,Ci)表示聚類Cj中的點x*與另一聚類Ci(i≠j)中所有的點之間的平均不相似度,a(x*)表示聚類Cj中的點與同聚類中其他所有點的平均不相似度。由此,可以計算出整個樣本空間中所有點的Silhouette指標的平均值Silaverage (16) Silaverage值可以有效反映聚類結果的質量,Silaverage>0.5表示各個不同聚類間具有明顯的可分離性,Silaverage值越大表示聚類質量越好[15]。 作為一種簡單、直觀、有效的非參數模式識別方法,KNN既能用于分類,又能用于回歸,因此被廣泛應用[16,17]。但是KNN算法有兩個非常明顯的缺點:計算量過大和受不均衡樣本影響。為了改進KNN算法的這兩個不足之處,本文特別提出了一種嵌套式的KNN算法,稱為Nested KNN。 對于一段足夠長的、包含N個樣本點的歷史時間序列,可構建基于原始KNN的預測模型 x(t+λ)=KNN(N,k) (17) 首先,用歐氏距離作為相似度測度,計算測試點x(t)與任意樣本點xn(n=1,2,…,N)的相似度 S(x(t),xn)=-‖x(t)-xn‖2 (18) 將S進行排序,找到前k個最大的S值和最相似的k個最鄰近元xj(j=1,2,…,k),其中k (19) 針對KNN的兩大不足之處,本文特別在以上模型的基礎上,將KNN改進為兩層嵌套式算法Nested KNN。該算法由三個函數:NKNN、NKNN1和NKNN0組成。其中NKNN作為主函數,對應整個算法的輸入-輸出,并調用NKNN1找到與輸入測試點最相似的聚類中心和相應的聚類;NKNN1再調用NKNN0在前一步輸出的聚類中找到與測試點最相似的k個最鄰近元用于回歸預測。具體如下: 函數NKNN1, 輸入預測點Xt+λ的前一點Xt=DR(t,T)和AP聚類輸出的r個類Ci(i=1,2,…,r)的集合C和各個聚類中心ei(i=1,2,…,r)的集合E,輸出與Xt最相似的聚類中心enearest和相應的聚類Cnearest,即 (Cnearest,enearest)=NKNN1(Xt,C,E,k=1) (20) 計算Xt與任意聚類中心ei(i=1,2,…,r)之間的相似度S(Xt,ei)。當S(Xt,enearest)為最大值時,enearest就是與Xt最相似的聚類中心,由此,可以得到以enearest為代表的聚類Cnearest,并將Xt歸為此類。 函數NKNN0,輸入Xt和Cnearest,輸出Xt+λ,即 (Xt+λ)=NKNN0(Xt,Cnearest,k) (21) (22) 其中參數k直接影響輸出結果。在實際的測試中,具體的不同樣本都對應于不同的最優k值,因此,為了得到更好的預測效果,本文將通過模型訓練,找到最優的k值。 函數NKNN,輸入Xt、C和E,先調用NKNN1輸出Cnearest和enearest,再調用NKNN0輸出Xt+λ,即 (Xt+λ)=NKNN(Xt,C,E,k) (23) 其中有Xt+λ=DR(t+λ,T),由此可以得出RR(t+λ)。 在Nested KNN算法中,NKNN1只需要計算測試點Xt與各個聚類中心之間的相似度,因此較KNN算法極大地減少了計算量。同時在NKNN0中,只需要計算測試點Xt與其最相似的聚類中心所在聚類Cnearest中的各個點之間的相似度,因此有效避免了不均衡樣本的問題。 在構建一個具體的PANK預測模型時,需要設定三個關鍵的模型結構參數:m,λ,k。其中m表示截取歷史金融時間序列的滑動窗口寬度;λ表示預測未來時間序列的步幅;k表示所取最鄰近元的個數。由此,可以將(3)式和(4)式中的PANK模型表達為 PANK:RR(t+λ)=NKNN{AP*[PCA(DR(t,m))],k} (24) 其中AP*=FE(AP)表示聚類提取預測輸入的過程。 對于時間序列預測模型的效能測度,我們常見的指標有均方根誤差(Root Mean Square Error, RMSE)[18]、平均絕對百分比誤差 (Mean Absolute Percentage Error, MAPE)[19]和平均絕對誤差(Mean Absolute Difference, MAD),用來測度實際值與預測值偏差。然而,對于量化投資而言,只有在預測趨勢方向有了顯著的正確率后,這些效能測度指標才有意義。因此,本文對于具體PANK預測模型的效能測度將采用衡量預測趨勢方向正確性的命中率(Hit Rate,HR)[20] (25) 浮動匯率制度在世界市場有效,大家對外匯市場廣泛關注,為了避免外匯市場風險,提出了各種匯率趨勢預測的模型[21,22]。與此同時,中國的股市,如滬深300股指等也受到了研究者的關注[23]。在本文的模型實證部分,我們構建了兩個具體的PANK預測模型,分別對歐元兌美元匯率和滬深300指數真實的歷史數據進行預測實證。 PANK_EURUSD_D1預測模型針對歐元兌美元匯率日線收盤價數據,對t+1日線收益率進行預測,該模型可從(24)式具體化為 PANK_EURUSD_D1:RR(t+1) =NKNN{AP*[PCA(EURUSD_D1_DR(t,m))],k} (26) 模型訓練和測試的歷史數據集由2002年11月1日至2017年11月24日期間的3909個交易日數據組成,前面時段的3128個數據點用于樣本內訓練,后面時段的781個數據點用于樣本外檢驗。表1顯示了PANK_EURUSD_D1預測模型的樣本外檢驗預測命中率結果,其中在m=25和k=5時,取得了最高的命中率0.80(80%),這表明PANK_EURUS_D1模型是一種性能優良的匯率預測模型。 表1 PANK_EURUSD_D1 預測歐元兌美元匯率t+1日線收益率的命中率 PANK_HS300_D1預測模型針對滬深300指數日線收盤價數據,預測t+1日線收益率,該模型可從(24)式具體化為 PANK_HS300_D1:RR(t+1) =NKNN{AP*[PCA(HS300_D1_DR(t,m))],k} (27) 模型訓練和測試的歷史數據集由2002年1月4日至2017年7月28日期間的3775個交易日數據組成,前面時段的3020個數據點用于樣本內訓練,后面時段的755個數據點用于樣本外檢驗。表2顯示了PANK_HS300_D1預測模型的樣本外檢驗預測命中率結果,其中在m=25和k=3時,取得了最高的命中率0.80(80%)。該實證結果表明PANK_HS300_D1模型仍然具有良好的預測效能。 表2 PANK_HS300_D1預測滬深300指數t+1日線收益率的命中率 為了進一步對PANK模型的預測效能進行評價,本文另外構建了兩個具體的KNN預測模型和兩個具體的AP+Nested KNN預測模型與之進行比較。 KNN_EURUSD_D1:RR(t+1) =KNN{[EURUSD_D1_DR(t,m)],k} (28) KNN_HS300_D1:RR(t+1) =KNN{[HS300_D1_DR(t,m)],k} (29) AP+NKNN_EURUSD_D1:RR(t+1) =NKNN{AP[EURUSD_D1_DR(t,m)],k} (30) AP+NKNN_HS300_D1:RR(t+1) =NKNN{AP[HS300_D1_DR(t,m)],k} (31) 為了更直觀地對六個具體模型的預測效能進行比較,我們選取了每個模型預測的最高命中率。表3顯示了對比結果,PANK預測模型不管是在外匯市場還是在股指上都有著最優的預測效果,由此可以說明PCA、AP和Nested KNN在PANK模型中都是有效果的,能夠有效改進KNN模型的預測效果。表3中不同模型的預測效能對比結果表明PANK預測效能優于AP+Nested KNN,而AP+Nested KNN又是優于KNN預測模型的。這正如Krogh和Vedelsby[24]證明的一樣,“當構成組合預測模型的單一模型足夠精確且足夠多樣化時,組合預測模型一定能獲得比單一模型更好的預測效果。” 表3 PANK模型與其他相關模型的預測效能比較 本文提出的PANK模型,是一種集成PCA、AP和Nested KNN算法的金融時間序列預測的計算智能模型。從整體結構上看,該模型具有PCA+AP的特征提取過程和Nested KNN回歸預測兩大部分,是具有創新性的。而模型中的Nested KNN算法是本文針對KNN算法本身的缺陷,提出的一種嵌套式的KNN改進算法。該算法由三個函數組成了兩層計算:(1)在PCA+AP輸出的聚類中心集中進行計算,并找到最相似的聚類中心及所在類。(2)在第一層輸出的聚類中進行計算,并找到最相似的k個最鄰近元進行回歸預測。這樣的分層計算比原始的KNN算法具有更有效的分類效果和更快的運算速度,從而能夠更有效地對金融時間序列進行回歸預測。為了驗證PANK模型的有效性,本文在預測歐元兌美元匯率和中國基準指數滬深300上進行了實證,對日線收益率進行了預測。實證結果表明PANK模型的預測性能明顯優于KNN和AP+Nested KNN預測模型,在每日時間框架內,最佳命中率均達到0.80(80%)。 在后續的研究中,我們的金融時間序列預測模型可以從以下方面進行改進研究:(1)將線性變換PCA換成一種更適合金融時間序列的非線性方法,比如“自編碼器”。(2)將歐氏距離換成一個更適合金融時間序列相似性度量的方法,以提高模型預測性能。(3)將KNN換成更有效的非線性預測模型,比如“隨機森林”。3 PANK預測模型的三個組成部分及其算法
3.1 主成分分析(PCA)
3.2 仿射傳播聚類(AP)
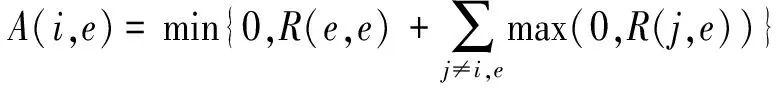
3.3 嵌套式k-最鄰近元(Nested KNN)
4 PANK預測模型的結構參數和效能測度
4.1 PANK預測模型的結構參數
4.2 PANK預測模型的效能測度
5 PANK預測模型的實證分析
5.1 PANK_EURUSD_D1預測歐元兌美元匯率日線收益率
5.2 PANK_HS300_D1預測滬深300指數日線收益率
5.3 與KNN和AP+Nested KNN預測模型的實證比較
6 結論與展望

