集成TEO解調和隨機共振的行星齒輪箱早期故障診斷方法

張俊 鐘敏 張建群 姚立綱 鄭近德

摘要：針對行星齒輪箱早期微弱故障難以診斷的問題，提出一種結合Teager能量算子（TEO）解調和隨機共振增強輸出的方法以實現故障特征提取。首先，對行星齒輪箱振動信號進行經驗模式分解（ EMD）并選取包含故障信息的分量信號，使用TEO解調運算獲得分量信號的解調信號。其次，為滿足隨機共振系統的小參數條件，將解調信號做適當壓縮處理并進行頻率二次采樣。再次，以定義的隨機共振系統輸出信噪比為適應度函數，采用粒子群算法優化隨機共振系統的結構參數，進而重構隨機共振系統以實現信號、噪聲以及非線性系統的最佳匹配。最后，將信號重新輸入參數優化后的隨機共振系統實現故障特征的增強提取。仿真和實驗均表明：該方法獲取了隨機共振系統的大信噪比輸出，實現了強噪聲下微弱故障特征的準確和高效提取，是一種行之有效的行星齒輪箱早期微弱故障診斷方法。

關鍵詞：故障診斷;行星齒輪箱;能量算子;經驗模式分解;隨機共振

中圖分類號：TH165+.3;TH132.4

文獻標志碼：A

文章編號：1004-4523 （2019） 06-1084-10

DOI：10. 16 385/j. cnki. issn. 1004-4523. 2019. 06. 018

引言

行星齒輪傳動因其具有體積小、傳動比大和承載能力強等優點，在各類工業機械中得到廣泛應用。在某些重要領域行星齒輪箱一旦發生故障將引起極其嚴重的后果，因此開展行星齒輪箱的故障診斷并探索高效的故障診斷方法勢在必行。

對振動信號包含的故障信息進行提取是齒輪箱故障診斷的有效方法。齒輪早期故障信號往往非常微弱，容易被噪聲淹沒，因此常規的信號處理方法在提取齒輪微弱故障信號時失效[1]。針對齒輪箱微弱故障信號提取問題，眾多學者進行了有益的探索。胥永剛等[2]利用復小波結合形態分量分析對信號進行降噪重構獲得故障信息;孫海亮等[3]采用多小波閾值降噪方法對軋機齒輪箱故障特征進行了提取。W ang等[4]采用集合經驗模式分解（EEMD）實現了風電齒輪箱軸承故障信號的分離提取;Cheng等[5]結合EEMD和熵特征融合進行了行星齒輪箱故障信息的提取;采用類似方法的研究還有文獻[6-7]。孟玲霞等[8]運用盲源分離技術對風電齒輪箱的齒輪磨損進行了預報;Li等[9]使用盲源分離技術對船用齒輪箱進行了故障診斷。需要指出的是，上述的小波分析與EEMD等方法均是通過對信號進行振動模式的分解以獲得故障所引起的振動分量。但是，當故障信號所具有的能量極小而噪聲占據主導時，信號分解的結果將出現明顯的模態混疊現象，單獨使用這類方法不易實現故障信號的有效提取。而盲分析技術存在欠定以及對非平穩信號分離困難等問題，限制了其實際應用效果。

不同于小波分析與EEMD等方法，隨機共振利用信號、噪聲與非線性系統的協同作用，以噪聲能量增強周期信號的輸出，來實現微弱周期信號的提取[10]。文[11-12]等較早地將隨機共振方法運用在直升機減速器齒輪點蝕故障診斷以及轉子碰摩故障分析。調節隨機共振系統的結構參數，可以有效誘導隨機共振，但早期的研究往往是依靠經驗來選取隨機共振系統的結構參數，其操作難度較大，故一些學者提出結合智能優化算法的自適應參數調節隨機共振方法，并將其運用于故障診斷。Li等[13]采用遺傳算法優化隨機共振系統的結構參數，并將結合遺傳算法優化的隨機共振方法用于軸承故障的診斷;Lei等[14]采用蟻群算法融合隨機共振對行星齒輪箱缺齒故障進行了診斷;謝有浩等[15]采用魚群算法得到優化參數的隨機共振，實現對齒輪斷齒故障的診斷;李繼猛等[16]等采用粒子群算法優化隨機共振系統，并將其運用于水輪機故障信號的提取。

綜上所述，當前采用隨機共振方法對行星齒輪箱早期微弱故障進行診斷的研究較少。相較于定軸齒輪箱，行星齒輪箱發生故障時其振動信號具有以下特點[14]：從嚙合點到固定傳感器的信號傳遞路徑是時變的，信號調制現象顯著;在信號頻譜中，不再嚴格具有以嚙合頻率及其倍頻為中心的故障邊頻帶;處于低頻段的故障特征容易被噪聲淹沒。以上特點增加了行星齒輪箱早期故障的診斷難度，而信號預處理是降低診斷難度的有效途徑。在已有的研究中，采用隨機共振方法提取故障特征前多未對信號進行充分預處理，限制了診斷效果。解調是常用的一種信號預處理方法。相較于Hilbert解調，Teager能量算子（Teager Energy Operator，TEO）解調在精度和實時性上有顯著優勢，因此TEO廣泛應用于機械故障診斷領域中的信號解調分析[17-18]。

有鑒于此，針對行星齒輪箱早期微弱故障難以診斷的問題，提出基于TEO解調和隨機共振的行星齒輪箱早期故障診斷方法。該方法的基本思路是：先對齒輪箱振動信號進行EMD分解以選取包含故障信息的分量信號，再利用TEO運算獲得該分量信號的解調信號;對解調信號進行壓縮和二次采樣以滿足隨機共振的小參數條件;將信號輸入隨機共振系統并計算定義的隨機共振輸出信噪比，使用粒子群算法優化系統的結構參數并重構隨機共振系統;將信號重新輸入隨機共振系統，最終實現行星齒輪箱微弱故障信號的隨機共振增強提取。下文將圍繞這一方法的各環節做具體闡述，并分別結合含故障行星齒輪箱的仿真信號與實測信號分析，對所提方法的有效性予以證實，希望為行星齒輪箱早期微弱故障診斷提供一種行之有效的技術解決途徑。由于EMD方法在眾多文獻中有使用，故本文只使用此方法，不再對其進行詳細的理論介紹，可參閱文獻[17]。

1 TEO解調方法

Teager在研究語音建模時，提出了一種信號分析算子。定義信號x（t）的Teager能量算子φ為

對一般形式的調幅一調頻（AM—FM）信號[17]

x（t）=a（t） cosφ（t）

（2）式中 a（t）為調制幅值;φ（f）為調制相位。

由信號x（t）及信號微分x（t）的Teager能量算子實現信號的瞬時幅值和瞬時頻率解調：

相較于Hilbert解調，TEO解調具有精度優勢，不妨以下述的AM-FM信號為例予以說明：x（t）=[1+0. lcos（2∏fst）]cos[2∏fmt+sin（2∏ f，t）]其中，fm =10 Hz;fs=0.2 Hz; fl=0.3 Hz。

圖1為分別使用兩種解調方式的解調結果。直接觀察可知，TEO解調對調制信號的恢復效果優于Hilbert解調，端點附近尤為明顯。從量化指標上看，TEO幅值解調和頻率解調的均方誤差（MSE）值分別只有0.00 3 3和1. 7097，而Hilbert解調MSE值分別為0.0214和2.5635，表明TEO解調具有較高精度。

需要指出的是，TEO解調對噪聲較敏感，故對多分量信號的解調效果往往不夠理想。鑒于此，對信號預先進行EMD分解以獲得包含故障信息的本征模式分量（IMF），再對其進行TEO解調。

2 微弱信號隨機共振檢測方法

2.1 雙穩隨機共振系統模型

周期信號驅動的雙穩態隨機共振系統可以用以下的郎之萬方程（Langevin Equation，LE）來表示[19]式中 U（x）為對稱雙穩態勢函數，其中a和b為其形狀參數即隨機共振系統參數;s（t）為多頻周期信號;Ai和fi分別為第i個周期分量信號的幅值和頻率;n（t）為高斯白噪聲，滿足：1）噪聲均值E[n（t）]=O;2）噪聲相關矩E[n（t）n（t'）]=2Dδ（t一t'），即不同時刻噪聲互相獨立。S（t）+n（t）為混合噪聲與周期信號的系統輸入，x為系統的輸出。

如圖2所示，勢函數U（x）具有兩個穩定的極值點x=±a/b（勢阱）和一個不穩定的極值點x=0（勢壘），勢壘高度△V =a2/（4b）。

對上述系統給予輕微的噪聲干擾，將導致粒子Pl最終穩定在定態解x=±a/b處。假想粒子在噪聲和周期信號協同下，克服勢壘高度△V并在兩勢阱之間做躍遷運動，當躍遷頻率正好等于周期信號的頻率，系統出現隨機共振現象。

外界噪聲驅動下，粒子P2在兩個穩態點之間的平均躍遷頻率fM為

由式（6）可知：（1）當參數a和b確定時，躍遷頻率取決于噪聲強度D，極限躍遷頻率a/（2b∏），即改變噪聲強度可以誘導隨機共振;（2）噪聲強度一定時，改變參數a或b將導致勢壘高度變化，從而改變粒子的躍遷頻率，同樣可以實現隨機共振。

控制噪聲強度來誘導隨機共振具有較大的操作難度，故在工程中常通過調節結構參數a和b實現系統在參數驅動下的隨機共振。

2.2 隨機共振小參數條件

隨機共振需滿足小參數條件，即驅動信號的幅值和頻率以及噪聲強度均比1小得多。然而，實際工況中采集的信號一般難以滿足小參數條件。為此，需要對信號進行預處理。

為滿足噪聲強度的小參數條件，需對信號進行壓縮處理。首先將有用信號和噪聲統一按噪聲處理，得到噪聲方差的估計值δ2x至，再選取適當的信號壓縮比q對信號進行q倍壓縮，使得壓縮后的噪聲方差a2x=a2x/qz滿足要求。

采用文獻[20]提出的二次采樣方法來滿足信號頻率的小參數要求。假設信號采樣頻率為fsp，特征信號的頻率為fs。設定頻率變換比R，則可以得到二次采樣的頻率f cr=fsp/R。以h=1/fcr作為數值計算步長，將信號輸入雙穩隨機共振系統，進行數值迭代獲得系統輸出。若輸出信號中獲得的小參數特征頻率為fs'，進行尺度恢復即可得到特征頻率fs= fs'×R。

2.3 隨機共振輸出信噪比

隨機共振輸出信噪比定義為特征信號功率與背景噪聲功率的比值，即式中 S（fs）為特征信號功率，通過計算輸出頻譜中特征信號頻率fs處幅值y（fs）的平方可得，N（fs）為背景噪聲功率，需做進一步估計。

由于難以對實際采集的齒輪箱振動信號進行精確的噪聲功率計算，故在上述公式基礎上提出適用于離散的實測含噪信號的信噪比公式式中 Y（k）為系統輸出信號頻譜中特征頻率fs所對應的第k個傅里葉點處的幅值;N（fs）為噪聲功率的估計值，定義為系統輸出頻譜中第k點左右各M個點（不包含k點）的平均功率，M的選擇與采樣頻率fsp有關，采樣頻率高則M取較大。

3 粒子群優化算法（ PSO）

為保證參數調節隨機共振的效果，需要根據信號的不同自適應地選擇參數a和b。為此，采用PSO算法，以式（8）定義的輸出信噪比為適應度函數，對隨機共振系統參數a和b進行優化。

PSO算法中，粒子在一個N維空間進行搜索，則粒子i的信息可用兩個N維向量來表示：粒子i的位置X i =（xil，xi2，…，XiN）T，飛行速度vi=（ui1，ui2，…，uin）T，根據以下兩式更新粒子信息：式中 d為搜索維數;ukid和xkid分別為粒子i在第k次迭代中第矗維的速度和位置;Cl，C2為學習因子;randk1，randk2為[O，1]之間的均勻隨機數;Pbestkid為第k次迭代，粒子i第d維最優位置;Gb estkd為第k次迭代，粒子中第d維最優位置。

PSO算法的具體步驟如下：

（1）種群的初始化。設定學習因子Cl和C2，種群規模M，最大迭代次數N max，速度范圍[Vmin，V max]，a，b的搜索范圍。產生初始種群并計算適應度。

（2）進化和更新。進入主循環，根據式（9）和（10）更新每個粒子的速度和位置，計算適應度并更新個體最優位置Pbest和全局最優位置Gbest，將本次迭代全局最優Gbest賦予Gbestc。

（3）迭代和更新。進行下一次迭代，重復步驟（2）更新Gbestc，達到最大迭代次數Nmax，則算法停止。

4 仿真數據分析

為驗證本文所提方法的有效性，首先進行仿真信號的分析。不失一般性，以下述簡化的太陽輪局部故障信號模型[21]為例式中 COS（2∏fmt）為由嚙合剛度周期變化引起的基礎嚙合振動部分;1- cos（2∏fsrt）為太陽輪旋轉調幅函數;l+Acos（2∏fst）為太陽輪局部故障調幅函數;Bsin（2∏fst）為太陽輪局部故障調頻函數;n（t）為模擬實際工況所添加的背景噪聲信號。

設定各項參數如下：嚙合頻率fm=1024 Hz;太陽輪旋轉頻率fsr=16 Hz;太陽輪局部故障頻率fs=42 Hz;故障的調幅和調頻強度設定A=B=0.1;添加均值為O、信噪比為-1 dB的高斯白噪聲。信號采樣頻率fsp=5000 Hz，采樣總時間為Is。

對信號進行EMD分解，得到前5個本征模式分量IMFi -IMFs如圖3所示。

對各分量進行TEO頻率解調，IMFi -IMF5信號的瞬時頻率分別圍繞頻率1 000，8 80，45 0，2 2 0以及115 Hz上下波動。圖4為IMFi分量的TEO頻率解調結果，由于行星齒輪箱輪齒發生故障時，一般表現為以嚙頻為載波頻率的故障調制現象，因此可認定IMFi是包含故障信息的有效分量信號，選取IMFi作進一步處理。

對IMFi進行TEO幅值解調和FFT運算，得到如圖5所示的TEO解調包絡頻譜，同時圖中右上方給出的是IMFi的時域波形。

觀察得知：頻譜峰值出現在太陽輪旋轉頻率fsr=16 Hz處，時域波形中出現的較明顯周期信號（9T=O. 56 s，f=16. 07 Hz）與其相吻合;故障特征頻率fs=42 Hz處的幅值很小。結果表明，信號中太陽輪旋轉的調幅作用占據主導，微弱的故障特征被噪聲淹沒，使用“EMD+TEO解調”方法未能提取到故障特征，需對解調信號做進一步處理。

將含噪解調信號僅當成噪聲處理，計算得到信號的噪聲方差估計δ2x=0.6 618，噪聲強度不滿足小參數條件。因此，設定信號的壓縮比q=30，以此壓縮比對信號進行壓縮，得到壓縮后信號的噪聲方差估計δ2x=7. 35×10_4。信號的采樣頻率5000 Hz，亦不能滿足頻率小參數要求，設定頻率變換比R=1250，則二次采樣頻率fcr=5000/1250=4 Hz。

使用壓縮后的信號作為隨機共振系統的含噪輸入，以二次采樣頻率確定的步長h=l/fcr =0. 25 s進行數值求解系統輸出。對式（5）所示朗之萬方程的數值求解采用文獻[19]提出的適用于雙穩隨機共振方程離散求解的四階龍格一庫塔法，概括如下式中 h為步長，x為系統的輸出，un為混合噪聲與信號的系統輸入的第n個點離散數據采樣點。

由式（8）計算輸出信噪比并作為適應度函數，使用PSO優化得到的隨機共振系統結構參數的最優組合為（a=10，b=3. 74），重構得到針對本問題的最優隨機共振系統模型。將經過前述方法處理得到的小參數信號重新輸入最優隨機共振模型，得到仿真信號的隨機共振提取結果，如圖6所示。

觀察可知：在隨機共振輸出時域波形中，信號的低頻周期特征得到了顯著的增強;頻譜圖中，頻率成分fs'0. 0336 Hz處出現了明顯譜峰，對該成分做R =12 50尺度恢復正好等于太陽輪局部故障特征頻率fs=42 Hz。此時的輸出信噪比SNRout=28. 62dB，而同樣利用式（8）計算的輸入信噪比為7.65dB，信噪比增益顯著。顯然，采用本文所提方法可實現太陽輪局部微弱故障特征的增強輸出。

5 實驗數據分析

為進一步驗證提出方法的有效性，搭建如圖7所示的動力傳動故障模擬試驗臺（DDS）。該實驗臺主要由驅動電機、單級行星齒輪箱、兩級平行軸齒輪箱、磁粉制動器以及數據采集模塊組成。

如圖7所示，在行星齒輪箱太陽輪連續兩齒的齒根位置加工切深裂紋，裂紋深度為0.5 mm。該裂紋將使輪齒剛度降低，進而產生故障沖擊，因此能較好地模擬太陽輪發生早期故障的情況。在輸出端施加1.2 A（約46 N·m）的扭矩負載，驅動電機轉速為39. 26 Hz。使用加速度傳感器采集行星齒輪箱箱體的振動信號，采樣頻率fsp=12800 Hz，采樣總時間Is。單級行星齒輪箱的齒數參數如表1所示，行星輪個數為4，由齒數參數和輸入轉速，按下式計算行星齒輪箱各主要特征頻率，計算結果如表2所示。式中 fsr，fc，fm，fs分別為太陽輪轉頻、行星架轉頻、嚙合頻率以及太陽輪故障特征頻率;Zs，Zr，N分別為太陽輪齒數、內齒圈齒數以及行星輪個數。

利用本文方法，首先進行信號EMD分解，其前5個本征模式分量IMFl -IMF5如圖8所示。

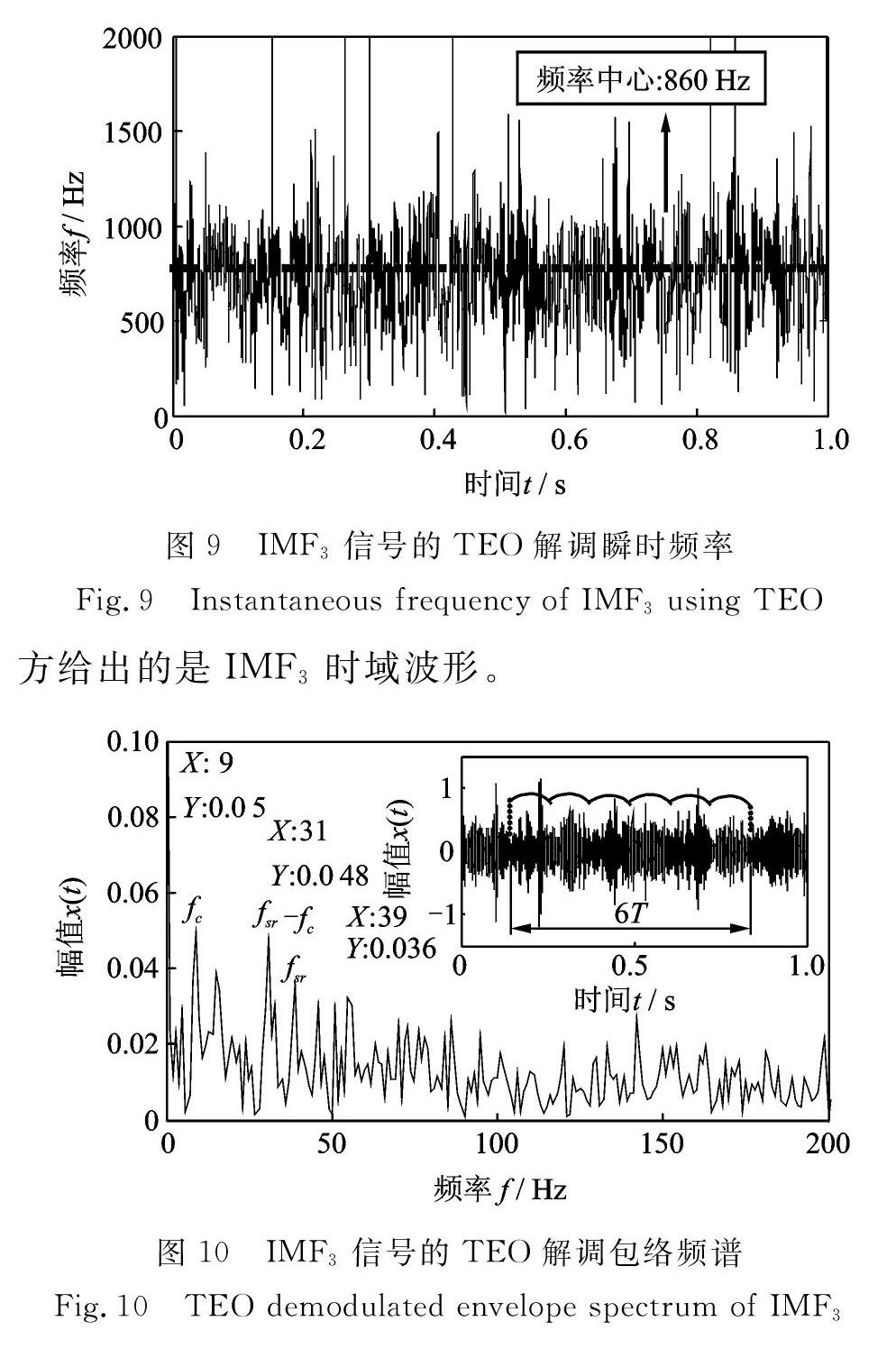
對各分量進行TEO頻率解調，IMFi -IMFs信號的瞬時頻率分別以頻率2100，1250，860，400以及220 Hz為中心上下波動。圖9為IMF3分量的TEO頻率解調結果，注意到IMF3大致圍繞嚙合頻率859 Hz波動，與仿真信號相同的選取原則，確定IMF3為下一步分析的目標分量。

對IMF3做TEO幅值解調和FFT運算，得到如圖1 0所示的TEO解調包絡頻譜，同時圖中右上

觀察時域波形發現，信號中存在較為明顯的周期調制信號，由6T=O.7 s，f=l/T≈8.57 Hz與行星架旋轉頻fc吻合。由于行星架旋轉和太陽輪旋轉引起行星輪一內齒圈以及行星輪一太陽輪嚙合位置的周期變化，固定位置的傳感器采集到的信號受到行星架旋轉和太陽輪旋轉的調制。反映在頻譜圖中，各譜線的峰值出現在行星架旋轉頻率fc和太陽輪旋轉頻率fsr以及它們的組合頻率如fsr-fc處，而故障特征頻率fs處未見明顯峰值。這一結果表明，微弱的裂紋故障特征完全被噪聲淹沒，使用“EMD+TEO解調”方法未能提取到故障特征。

將解調信號僅當成噪聲處理，噪聲方差估計值δ2x=0.4 4 5過大，故對信號進行q= 30倍的壓縮，壓縮后δ2x0. 445×10_4滿足要求;設定R=2560，則二次采樣頻率fcr為5 Hz，步長h=l/fcr =0.2 s，將信號帶人方程（12）求解郎之萬方程得到系統輸出。

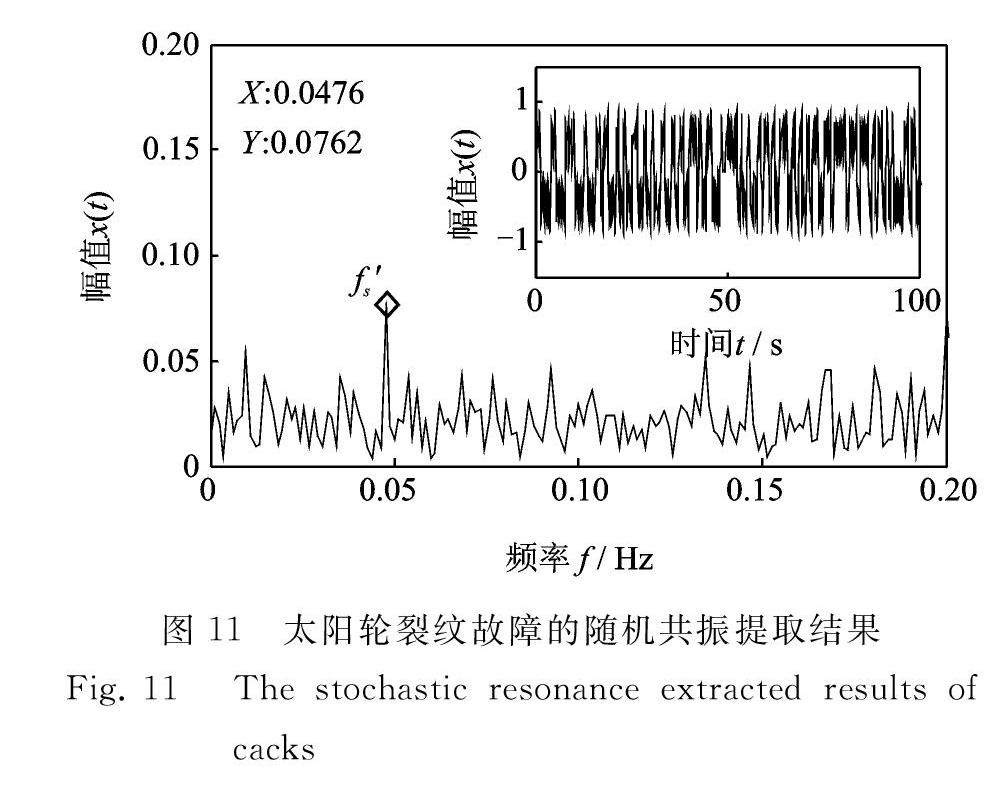
由式（8）計算輸出信噪比并作為PSO算法適應度函數，使用PSO算法得到的隨機共振系統結構參數的最優組合為（a=11. 122，b=11. 794）。隨后，利用最優參數a和b重構雙穩隨機共振系統。將前述處理后的小參數信號重新輸入系統，求解郎之萬方程得到系統輸出，如圖11所示。

觀察可知：在隨機共振的作用下，時域波形中信號的低頻周期性得到顯著增強;頻譜圖中，頻率成分fs'=0. 0476 Hz處出現明顯峰值，恢復尺度得到f=122 Hz，正好等于太陽輪局部故障頻率fs。此時SNRout =25. 62 dB，而同樣利用式（8）計算的輸入信噪比為-4. 11 dB，信噪比增益顯著。結果表明，針對實測振動信號，采用本文所提方法，微弱的太陽輪裂紋故障特征得到了有效提取。

行星齒輪箱由于其結構特點，在無故障條件下也存在明顯的調制現象，如行星架調制、太陽輪旋轉調制以及可能存在的其他誤差調制，且有可能造成對故障狀態的誤判。為驗證本文所提方法的可靠性，對實驗采集的一組無故障狀態下的振動信號進行分析。EMD分解（目標分量信號為IMF3）以及TEO解調的詳細過程不再贅述。PSO尋優獲得的隨機共振系統參數組合為（a=10. 667，b=ll. 264），此時隨機共振輸出信噪比為16. 28 dB。給出IMF3的TEO解調包絡頻譜以及對解調信號的隨機共振增強輸出結果，分別如圖1 2和1 3所示。

由圖1 2和1 3可知，相較于含太陽輪裂紋的箱體振動信號，無故障狀態下IMF3信號的時域波形較為平穩，無顯著的信號沖擊，包絡頻譜中出現行星架旋轉頻率及其倍頻的主導頻率成分;區別于故障狀態，行星架轉頻在隨機共振的作用下有所增強，而在故障特征頻率（fs'=0. 0476 Hz）處，未發現顯著高于周圍頻率成分幅值的譜峰，因此認定齒輪箱無故障。結果表明，所提出方法能夠有效地甄別出行星齒輪箱的健康/故障狀態，本文所提方法對行星齒輪箱輪齒早期故障的診斷結果是可靠的。

6 對比與討論

6.1 EMD分解對提取效果的影響

為說明對信號進行EMD分解的必要性，對上述仿真和實驗的太陽輪故障信號不經EMD分解，其余信號處理方式相同，同樣采用PSO優化參數a和b，對故障特征進行隨機共振提取。

對仿真和實驗信號，PSO優化得到的隨機共振系統結構參數最佳組合分別為（a=8. 563，b=13. 291）和（a=11. 187，b=7.768）。將信號輸入重構的隨機共振系統得到共振輸出，其結果如圖14所示。

由圖1 4可知，盡管故障特征頻率fs'得到了隨機共振增強，但對比圖6與1 1，其幅值明顯偏低，同時出現了較高幅值的干擾頻率成分，容易造成對故障狀態的誤判。

6.2TEO解調對提取效果的影響

為說明對信號進行TEO預解調的必要性，對上述仿真和實驗的IMF分量信號不經TEO解調，其余信號處理方式相同，同樣采用PSO算法優化參數a和b，對故障特征進行隨機共振提取。

對仿真和實驗信號，PSO優化得到的隨機共振系統結構參數最佳組合分別為（a=9. 818，b=12. 119）和（a=12. 554，a=3.361）。將信號輸入重構的隨機共振系統，獲得如圖1 5所示的隨機共振輸出。

由圖1 5可知，對仿真信號的提取結果中，故障特征頻率fs'得到了隨機共振增強，但是對比圖6，其幅值明顯更低。對實驗信號，盡管故障特征頻率fs'處幅值較高，但存在多處較明顯的干擾譜峰，其譜線分辨能力對比圖1 1較差，不利于故障辨別。

6.3 討論

為便于比較，表3列出了3種組合方法獲得的隨機共振輸出信噪比指標。

由表3可知，基于本文提出方法獲得的隨機共振輸出信噪比具有明顯優勢。相比之下，其余兩種組合方法，無論是輸出信噪比指標還是譜線分辨能力，其診斷效果均較差。對比結果表明，為獲得更好的診斷效果，進行故障特征的隨機共振提取前對信號進行EMD分解和TEO解調是必要的，這是由于EMD分解的過程實質也是信號降噪的過程，它降低了數據的復雜程度，因此對IMF信號進行隨機共振更容易實現故障特征的有效提取。同時由于箱體振動信號本身存在調制特性，而TEO能夠很好地提取包含故障信息的解調信號，降低故障提取難度。

7 結 論

（1）提出了一種基于TEO解調與隨機共振的行星齒輪箱早期故障診斷方法，成功實現了含太陽輪早期裂紋損傷的行星齒輪箱故障特征的準確提取。

（2）實際工況下的行星齒輪箱振動信號一般不滿足經典隨機共振的頻率及噪聲的小參數要求，需對其進行信號壓縮和二次采樣處理，才可滿足系統的小參數條件。

（3）單純基于EMD+SR的方法或TEO+SR的方法均難以實現行星齒輪箱早期故障的準確提取。

參考文獻：

[1] 李繼猛，張金鳳，張云剛，等，基于自適應隨機共振和稀疏編碼收縮算法的齒輪故障診斷方法[J].中國機械工程，2016，27（13）：1796-1801，1809.

Li Jimeng， Zhang Jinfeng， Zhang Yungang， et al.Fault diagnosis of gears based on adaptive stochasticresonance and sparse code shrinkage algorithm[J].China Mechanical Engineering 2016， 27 （13）： 1796-1801， 1809.

[2] 胥永剛，趙國亮，馬朝永，等，雙樹復小波域MCA降噪在齒輪故障診斷中的應用[J].航空動力學報，2016， 31（1）：219-226.

Xu Yonggang， Zhao Guoliang，Ma Chaoyong， et al.Denoising method based on dual-tree complex wavelettransform and MCA and its application in gear fault di-agnosis[ J]. Journal of Aerospace Power， 2016， 31（1）：219-226.

[3] 孫海亮，訾艷陽，何正嘉，多小波自適應分塊閾值降噪及其在軋機齒輪故障診斷中的應用[J].振動工程學報，2013，26（1）：127-134.

Sun Hailiang， Zi Yanyang， He Zhengjia. Multi-wave-let denoising with adaptive block thresholding and itsapplication in gearbox diagnosis of rolling mills[J].Journal of Vibration Engineering， 2013， 26（1）： 127-134.

[4] Wang J，Gao R X， Yan R.Integration of EEMD andICA for wind turbine gearbox diagnosis[J]. Wind En-ergy， 2014， 17（5）：757-773.

[5] Cheng G，Chen X， Li H， et al. Study on planetarygear fault diagnosis based on entropy feature fusion ofensemble empirical mode decomposition[J]. Measure-ment， 2016， 91： 140-154.

[6] Chen X H， Cheng G， Shan X L，et al. Research ofweak fault feature information extraction of planetarygear based on ensemble empirical mode decompositionand adaptive stochastic resonance[J]. Measurement，2015， 73： 55-67.

[7] Xiang J，Zhong Y.A fault detection strategy using theenhancement ensemble empirical mode decompositionand random decrement technique[J]. MicroelectronicsReliability， 2017， 75： 317-326.

[8] 孟玲霞，徐小力，蔣章雷.等，風電機組齒輪箱早期故障預警方法研究[J].儀器儀表學報，2016，37 （12）：2758-2765.

Meng Lingxia， Xu Xiaoli， Jiang Zhanglei， et al. Studyon the early fault warning method for wind turbinegearbox[J] Chinese Journal of Scientific Instrument，2016， 37（12）：2758-2765.

[9] Li Z，Peng Z.A new nonlinear blind source separationmethod with chaos indicators for decoupling diagnosisof hybrid failures： A marine propulsion gearbox casewith a large speed variation[J]. Chaos Solitons &Fractals the Interdisciplinary Journal of Nonlinear Sci-ence & Nonequilibrium & Complex Phenomena，2016， 89： 27-39.

[10] Benzi R， Sutera A， Vulpiani A. The mechanism ofstochastic resonance[J]. Journal of Physics A GeneralPhysics， 2015， 14（11）：L453.

[11]楊定新，胡蔦慶，楊銀剛，等，隨機共振技術在齒輪箱故障檢測中的應用[J].振動工程學報，2004， 17（2）：201-204.

Yang Dingxin， Hu Niaoqing， Yang Yingang， et al.Application of stochastic resonance in early fault detec-tion for intermediate gearbox of helicopter[J]. Journalof Vibration Engineering， 2004， 17（2）：201-204.

[12]陳 敏，胡蔦慶，秦國軍，等，參數調節隨機共振在機械系統早期故障檢測中的應用[J].機械工程學報，2009， 45（4）：131-135.

Chen Min， Hu Niaoqing， Qin Guojun， et al. Applica-tion of parameter-tuning stochastic resonance for de-tecting early mechanical faults[J]. Journal of Mechani-cal Engineering， 2009， 45（4）：131-135.

[13] 11 J，Zhang J. Adaptive multi-scale noise control en-hanced stochastic resonance method based on modifiedEEMD with its application in bearing fault diagnosis[J]. Shock and Vibration，2016，2016（3）： 1-13.

[14] Lei Y， Han D， Lin J，et al. Planetary gearbox faultdiagnosis using an adaptive stochastic resonance meth-od[J]. Mechanical Systems & Signal Processing，2013， 38（1）：113-124.

[15]謝有浩，劉曉樂，劉后廣，等，基于改進移頻變尺度隨機共振的齒輪故障診斷[J].農業工程學報，2016，32（8）：70-76.

Xie Youhao， Liu Xiaole， Liu Houguang， et al. Im-proved frequency-shifted and re-scaling stochastic reso-nance for gear fault diagnosis[J]. Transactions of theChinese Society of Agricultural Engineering， 2016， 32（8）： 70-76.

[16]李繼猛，陳雪峰，何正嘉，采用粒子群算法的沖擊信號自適應單穩態隨機共振檢測方法[J].機械工程學報，2011， 47（21）：58-63.Li Jimeng， Chen Xuefeng， He Zhengjia. Adaptivemonostable stochastic resonance based on PSO withapplication in impact signal detection[J]. Journal ofMechanical Engineering， 2011， 47（21）：58-63.

[17]程軍圣，于德介，楊 宇，基于EMD的能量算子解調方法及其在機械故障診斷中的應用[J].機械工程學報，2004， 40（8）：115-118.

Cheng Junsheng， Yu Dejie， Yang Yu. Energy opera-tor demodulating approach based on EMD and its ap-plication in mechanical fault diagnosis[J]. Journal ofMechanical Engineering， 2004， 40（8）：115-118.

[18]張文義，于德介，陳向民，齒輪箱復合故障診斷的信號共振分量能量算子解調方法[J].振動工程學報，2015，28（1）：148-155.

Zhang Wenyi， Yu Dejie， Chen Xiangmin. Energy op-erator demodulating of signal's resonance componentsfor the compound fault diagnosis of gearbox[J]. Jour-nal of Vibration Engineering， 2015， 28（1）：148-155.

[19]楊定新，微弱特征信號檢測的隨機共振方法與應用研究[D].長沙：國防科學技術大學，2004.

Yang Dingxin.On methodology and application ofweak characteristic signal detection based on stochasticresonance[D]. Changsha： National University of De-fence Technology，2004.

[20]冷永剛，王太勇，李瑞欣，等，變尺度隨機共振用于電機故障的監測診斷[J].中國電機工程學報，2003，23 （11）：111-115.

Leng Yonggang， Wang Taiyong， Li Ruixin， et al.Scale transformation stochastic resonance for the moni-toring and diagnosis of electromotor faults[J]. Pro-ceedings of The Chinese Society for Electrical Engi-neering， 2003， 23（11）：111-115.

[21]馮志鵬，趙鐳鐳，褚福磊，行星齒輪箱齒輪局部故障振動頻譜特征[J].中國電機工程學報，2013， 33（5）：118-125.

Feng Zhipeng， Zhao Leilei， Chu Fulei. Vibration spec-tral characteristics of localized gear fault of planetarygearboxes[J]. Proceedings of The Chinese Society forElectrical Engineering， 2013， 33（5）：118-125.